Az idegrendszeri dinamika modell alapú vizsgálata: az egyedi idegsejtektől a hálózatokig
|
|
|
- Natália Fekete
- 8 évvel ezelőtt
- Látták:
Átírás
1 Az idegrendszeri dinamika modell alapú vizsgálata: az egyedi idegsejtektől a hálózatokig Somogyvári Zoltán Doktori (Ph. D.) értekezés Készült a Magyar Tudományos Akadémia Részecske és Magfizikai Kutatóintézetének Biofizikai osztályán Témavezető: Dr. Érdi Péter, az MTA doktora, tudományos tanácsadó, egyetemi magántanár, Henry R. Luce professzor, a Biofizika osztály osztályvezetője. Szentágothai János Idegtudományi Doktori Iskola Semmelweis Egyetem Budapest, 2006
2 Szentágothai János Idegtudományi Doktori Iskola Doktori Iskola vezetője: Dr. Réthelyi Miklós, az MTA Doktora Funkcionális idegtudományok Doktori Program Programvezető: Dr. Vizi E. Szilveszter, az MTA Doktora Védés: Elnök: Tagok: Hivatalos bírálók:
3 Most csak tükör által homályosan látunk, de akkor majd színről színre. Pál apostol első levele a korintusiakhoz
4 Köszönet Köszönet kedves feleségemnek és múzsámnak Fanninak mindenért. Köszönöm Árminnak, kisfiamnak a kreativitását és Johannának, kislányomnak a kedvességét. Köszönöm Anyukám minden áldozatvállalását. Köszönöm témavezetőmnek Dr. Érdi Péternek, hogy megmutatta e csodálatos tudományterület szépségét, segített és tanított sok éven át. Köszönöm kutatócsoportunk minden tagjának: Dr. Bazsó Fülöpnek, Csárdi Gábornak, Huhn Zsófinak, Dr. Kiss Tamásnak, Nepusz Tamásnak, Orbán Gergőnek, Dr. Szalisznyó Krisztinának, Ujfalussy Balázsnak, Zalányi Lacinak és minden volt tagjának: Dr. Aradi Ildikónak, Dr. Barna Gyurinak, Borbáth Gábornak, Földy Csabának, Dr. Grőbler Tamásnak, Dr. Lengyel Máténak, Papp Gergőnek, Payrits Szabolcsnak és Szathmári Zoltánnak, hogy a barátság örömteli légkörében dolgoztunk együtt. Köszönöm az inspiráló szellemi környezetet, a számtalan beszélgetést és a nyíltságot egymás gondolatai iránt. Köszönöm csoporton kívüli szerzőtársaimnak: Dr. Székely Györgynek, Dr. Szente Magdolnának, Dr. Barna Barbarának, Dr. Szász Andrásnak, Dr. Ulbert Istvánnak, Dr. Világi Ildikónak, Dr. Halasy Katalinnak és Borbély Sándornak a közös munkát, hogy megoszthattuk egymással különböző látásmódunkat. Külön köszönöm Dr. Andai Attilának, akivel együtt vágtunk neki az agy felfedezésének és első cikkünket írtuk. Köszönöm tanáraimnak és mindenkinek aki példát adott eddig életemben. Somogyvári Zoltán
5 Tartalomjegyzék Bevezető 1 Célkitűzések 3 1. Idegsejtek tüzeléseinek modell alapú analízise Bevezetés a modell alapú analízishez A direkt és az inverz probléma A Poisson inverz probléma és az EEG/MEG alapú képalkotó eljárások A monopólus modell Módszerek In vivo mérések Számítógépes szimulációk Modell illesztés Eredmények A monopólus modell illeszkedésének vizsgálata in vivo mért adatokra Általános pontforrás modellek illeszkedésének vizsgálata in vivo mért adatokra Az ellenáram modell felépítése Az ellenáram modell vizsgálata szimulált adatokon i
6 Az ellenáram modell illeszkedésének vizsgálata in vivo adatokre és az adatok elemzése az ellenáram modell alapján Összefüggések Kortikális kiváltott epilepsziák CSD elemzése Bevezetés Módszerek Eredmények Összefüggések aminopyridin kezeléssel kiváltott epilepszia elemzése és modellezése Bevezetés Módszerek In vivo mérések Wavelet transzformáció Az attraktorok rekonstrunkciója A modell Eredmények A frekvencia spektrum változása a roham során A rendszer rekonstruált attraktorának változása a roham során A roham dinamikájának neuronhálózati modellezése Összefüggések Az elemzés eredményeinek értelmezése A modellhálózat aktivitásának értelmezése Az elemzés eredményeinek összevetése a szimulációkkal Véletlen Boole hálózatok állapotciklusainak vizsgálata Bevezetés A véletlen Boole hálózatok leírása ii
7 A hálózat felépítése Dinamika A dinamika analitikus leírása A lépéshossz változásainak leírása Az önelkerülő bolyongás leírása Eredmények Az eredmények megbeszélése Az értekezés témájához kapcsolódó saját közlemények jegyzéke Egyéb saját közlemények jegyzéke Irodalomjegyzék 102 iii
8 Bevezető Az emberi gondolkodás alapvető folyamata a világ modelljének megalkotása és a megalkotott világmodell alkalmazása azaz gondolatkísérletek végzése, a következmények előjelzése és a jósolt eredmények összehasonlítása a tapasztalattal. Ezek a lépések természetes részei mindennapi gondolkodásunknak, de számos új eredmény mutatja, hogy hasonló folyamatok önkéntelenül, tudatosság nélkül, folyamatosan zajlanak agyunkban. Agyunk folyamatosan modellezi a világot, jósol, összehasonlít és valószínűleg ennek figyelembe vételével módosítja és javítja a modellt. A világ modellezése, amit a szinonimának tekintve a világ szimbolikus reprezentációjának is nevezek, alapvető eleme az emberi gondolkodásnak. Ebből a szempontból nincs lényegi különbség a között ha azt állítjuk: A nap süt. vagy ha ezt: C dv m(t) dt = I m (t) (1) A két állítás számtalan szempontból különbözik. Más a két reprezentáció nyelve, az első szóbeli a második matematikai, az első modell statikus a második dinamikus, de közös bennük, hogy mindkét állítás a világ egy darabkájának modellje. Bennük szimbólumok reprezentálják a világ objektumait és más szimbólumok az objektumok közötti összefüggéseket. Ugyan azt a dolgot többféleképpen is lehet reprezentálni, modellezni és a különböző modelleket felváltva, de akár párhuzamosan is lehet használni. Míg az objektumok reprezentációi önkényesen megválaszthatóak, az objektumok között értelmezett transzfor- 1
9 mációk reprezentációinak már meg kell felelniük bizonyos törvényszerűségeknek ahhoz, hogy valóban a reprezentálják a világ összefüggéseit. A hétköznapi életben egy állítást igaznak vagy hamisnak tekintünk, ez azonban igencsak leegyszerűsítése egy állítás és a világ viszonyának. Ha egy állítást nem logikai formának, hanem reprezentációnak azaz modellnek tekintünk, akkor a reprezentáció igazságát nem, de hűségét számon kérhetjük. Egy transzformáció és a hozzá tartozó szimbólum rendszer akkor hű reprezentációja egy folyamatnak, ha a kiindulási állapot reprezentációjának transzformáltja megegyezik a folyamat eredményének reprezentációjával. Ez a kívánalom azonban még mindig elég tág teret hagy a sokféleségnek, ugyan azt a folyamatot sokféleképpen lehet hűen reprezentálni, sokféle hű modellt alkothatunk rá. E sokféle modell közt nem feltétlenül létezik legjobb, más más helyzetben illetve összefüggésben más más reprezentáció bizonyulhat hasznosabbnak illetve más más összefüggésekre mutathat rá. Ha a reprezentációs rendszert amelyben egy adott állítást teszünk rögzítjük, akkor újra felvethetjük az állítás igazságának kérdését. Azaz egy állítás igazságát nem lehet önmagában vizsgálni, csak a teljes reprezentációs rendszer részeként. A reprezentáció megalkotása azaz a modell alkotás folyamata így több szempontból is központi eleme kutatásomnak. Az agy egyik legfőbb feladata a modellalkotás, a világ reprezentációjának megalkotása, ugyanakkor a kutatás maga is egy modell alkotási folyamat. Ismét más szempontból tekintve, a modellek által új információhoz is juthatunk de a kutatás eredményeképpen létrejött gondolati kép is egy modell. Tehát a modellezés folyamata egyszerre jelenik meg mint a kutatás tárgya, eszköze, folyamata és eredménye. 2
10 Célkitűzések Értekezésem négy önálló kutatás eredményeiből állt össze és ezek eredményeit értekezésem négy számozott fejezete tárgyalja. Egy kutatás célkitűzései többféle szinten megfogalmazhatóak, a legáltalánosabbtól a legspecifikusabbakig, hiszen az agykutatásnak legáltalánosabb célja az agy működésének megértése, ugyanakkor minden egyes részeredmény, a dolgozat minden egyes ábrája felel egy kérdésre, teljesít egy célkitűzést. Ezért munkám célkitűzéseit általánosabb és specifikusabb módon is megfogalmazom. Kutatásom két alapeleme az elemzés és a modell alkotás, ha tehát általános értelemben akarom a célkitűzéseket megfogalmazni, akkor e két tevékenység célját kell megvizsgálni. A matematikai elemzés célja, hogy a matematikai eszközökkel minél több új információt nyerjünk ki a mért adatokból, míg a modellezés feladata, hogy az így kinyert információ töredékeket egységes gondolati képpé szervezze. Az összefüggés e két folyamat között azonban nem egyirányú. Az elemzés során alkalmazott matematikai eszközök miden esetben igénylik, hogy feltevéseket tegyünk a rendszerről amelyre alkalmazzuk azokat, tehát az elemzéshez szükséges egy előzetes gondolati kép, modell megléte. Másrészt egy új modell felállítása új elemzési módszerekhez és az adatok új értelmezéséhez, ezen keresztül pedig új információhoz vezethet. Az elemzés és a modell alkotás tehát egymást kölcsönösen előmozdítva viheti előre a megismerést. Munkám általános célkitűzése tehát a matematikai elemzés és modell alkotás egymást kölcsönösen feltételező módszerével közelebb kerülni az agy dinamikájának megértéséhez. A modellek és az elemzés e körforgásában legmesszebbre az első fejezetben tárgyalt kutatás jutott, itt az adatok elemzése új modell- 3
11 hez vezetett, az új modell új elemzési módszerhez, ami pedig új elemzési eredményekhez. A második fejezet csak az elemzésig jutott, a harmadikban az elemzés eredményei új modellt inspiráltak, míg a negyedik fejezet csak a modellezéssel foglalkozik. Értekezésemben egyre szélesedő perspektívából vizsgálom az idegrendszert, melyben nem csak a vizsgált rendszer mérete, de az absztrakció szintje is folyamatosan nő. Az első fejezet középpontjában az egyedi idegsejtek tüzeléseinek elemzése áll, a második fejezetben az agykérgi körök aktivitásának rétegek szerinti eloszlását vizsgálom in vitro szeparált kérgi szövetben. A harmadik fejezetben tovább tágul a kép és in vivo körülmények között elemzem és modellezem a kérgi epileptikus aktivitást, végül a negyedik fejezetben a neuronhálózatok dinamikai tulajdonságainak absztrakt modelljével fejezem be vizsgálódásaimat, amely a neuronhálózatok tulajdonságainak általános vizsgálatára ad alkalmat. Az egyre nagyobb léptékű képekben egyre általánosabb jelenségek vizsgálhatóak, ugyanakkor ez természetesen azzal jár, hogy a finom részletek elmosódnak, a képek egyre elnagyoltabbak lesznek. Nem akarok nem létező összefüggéseket erőltetni a különálló kutatási témák közé, de fel szeretném hívni a figyelmet a meglévő és esetleg kevésbé nyilvánvaló kapcsolatokra is. Az első három fejezet alapmotívuma az idegrendszerben elektródákkal rögzített elektromos jelek elemzése. Ezen belül, az első két fejezet központi eleme az áramforrás sűrűség eloszlás (Current Source Density, CSD) meghatározása a mért potenciálok alapján. A második fejezet összefoglalja azokat az eredményeket amelyeket a CSD módszer alkalmazásával nyertünk az agykéregben kiváltott epileptikus aktivitás elemzése során, míg az első fejezetben megmutatom, hogy a hagyományos CSD módszer nem alkalmazható egyedi idegsejtek esetében, de megmutatom azt is, hogy hogyan juthatunk hozzá a CSD információkhoz ebben az esetben. Az első fejezet egyik lényegi eleme tehát a CSD módszer továbbfejlesztése oly módon, hogy az alkalmassá váljék egyedi idegsejtek áramforrás eloszlásainak meghatározására. A második és a harmadik fejezet között szoros kapcsolatot teremt a kutatás tárgya: mindkettőnek alapja a mesterségesen kiváltott epileptikus aktivitás során rögzített elekt- 4
12 romos jelek elemzése. A második fejezetben in vitro körülmények között, agyszeleten, elsősorban a jelek térbeliségére, az agykérgi rétegek közötti eloszlására koncentrálva, míg a harmadik fejezetben in vivo, egész agyon és a jelek időbeli szerkezetére figyelve készült az elemzés. Ennek megfelelően különböznek az elemzés során alkalmazott matematikai eszközök: a térbeli eloszlásokat a CSD módszerével, míg az időbeli jeleket a wavelet transzformáció és a fázistér rekonstrukció módszerével vizsgáltam, illetve itt egy modellt is alkottam a jelenségek alatt meghúzódó lehetséges folyamatok leírására. A második és a harmadik fejezetben egyaránt megjelenik a 4-aminopyridin, mint görcskeltő anyag, de az in vitro kísérletekben még két további görcskeltő hatásának elemzésére is lehetőség nyílt. A harmadik és a negyedik negyedik fejezetben szoros kapcsolat van az alkalmazott modell rendszerek tulajdonságaiban. A harmadik fejezetben a neuronok modellezésére használt McCulloch-Pitts neuronok a lineárisan szeparábilis speciális esetei az általános Boole-függvényeknek, amelyekből felépülő véletlen hálózatok tulajdonságait a negyedik fejezetben tárgyalom. A tárgyalt négy önálló téma feldolgozása során az egyedi sejttől az agykérgi neuronkörökön keresztül eljutunk a neuronpopulációk általános viselkedéséig. Mivel a négy fejezet négy önálló kutatás eredményeit foglalja össze, a specifikus célkitűzéseket e négy kutatás szintjén lehet megfogalmazni. Az első fejezet célkitűzése, megtalálni a tüzelő idegsejtnek, mint térben eloszló áramforrásnak egy olyan modelljét, amely biztosítja, hogy a mikro elektróda rendszerekkel mért potenciál mintázatok alapján az idegsejt membránján folyó áramforrás eloszlás meghatározható legyen. Más szavakkal megalkotni azt a modellt, amely jól illeszkedik az idegsejtek tulajdonságaihoz és a mért adatokhoz, ugyanakkor elegendően leszűkíti a lehetséges megoldások terét ahhoz, hogy a Poisson egyenlet inverz feladatának megoldása egyértelmű legyen. Ismét másképpen fogalmazva célom egy új, egysejt CSD módszer megalkotása volt. A második fejezet célkitűzése az in vitro agykérgi szeletben három különböző görcskeltő anyag hatására létrejött epileptikus aktivitás során az áramforrás eloszlás, azaz a CSD 5
13 mintázatok jellegzetességeinek és különbségeinek meghatározása az agykéreg különböző rétegeiben. A harmadik fejezet célkitűzése, a 4-aminopyridin in vivo alkalmazása során létrejött epileptikus rohamok időbeli változásainak vizsgálata és a megfigyelt változások mögött meghúzó dinamikai rendszer egy modelljének megalkotása. A negyedik fejezet célkitűzése, hogy olyan analitikus leírást adjak a véletlen Boole hálózatok dinamikájáról, amely alapján a hálózat szerkezet és dinamika közötti összefüggés és a fázisátalakulás jelensége megérthető, valamint, hogy ez alapján analitikus közelítéseket adjak a hálózat dinamikájának főbb jellemzőire. 6
14 1. fejezet Idegsejtek tüzeléseinek modell alapú analízise 1.1. Bevezetés a modell alapú analízishez Az idegsejtek élettani működésének alapeleme az akciós potenciál létrehozása, mely a sejtből ki és az oda beáramló ionok révén elektromos potenciál változást hoz létre a sejtek közötti teret kitöltő elektrolit folyadékban. Ez a potenciál változás mérhető a sejten kívüli folyadékba merített mikroelektródákkal. Ha több mikroelektródot egymáshoz elegendő közelségben helyezünk el, egy idegsejt elektromos aktivitása több elektródán párhuzamosan mérhető, mérésünk eredménye egy téridőbeli elektromos potenciál mintázat lesz. A tapasztalat szerint az ilyen típusú mérési adatokban két lényeges komponens különböztethető meg: alacsonyabb frekvencia tartományban (0-500 Hz) az ún. helyi mezőpotenciál (local field potential, LFP) melynek fő forrásai a szinaptikus áramok, magasabb frekvencia tartományban (300 Hz fölött) pedig kisszámú egyedi sejt akciós potenciáljainak együttese mérhető (multi unit activity, MUA). Mindkét jeltípus az elektróda környezetében található sejtek membránján áthaladó ionáramok következménye, de átlagolódásuk során különböző hatások lépnek fel. A nagyagykéregben átlagosan 10 4 db szinapszis jut minden sejtre, igy posztszinaptikus áramimpulzusból is ennyiszer több van, mint keletkező akciós potenci- 7
15 álból. A posztszinaptikus áramimpulzusok tipikus időállandója ms, míg az akciós potenciált létrehozó áramok ms időtartományban folynak. Számos egyéb, kevésbé ismert tényező szintén befolyásolja, befolyásolhatja az átlagolódást, mint például az idegszövet frekvenciafüggő vezetőképessége illetve dielektromos állandója és az akciós potenciál érkezési idejének szórása a különböző axon végződések között. Mindezen hatások együttes eredményeképp valószínű, hogy a helyi mezőpotenciál nagyobb területen található és szám szerint több sejt aktivitásának eredménye, míg az egyedi akciós potenciálok csak a legközelebbi sejtek esetében mérhetőek. A szakirodalomban nem találtam becslést sem arra, hogy milyen távoli sejtek illetve mekkora agyterület sejtjeinek átlaga a lokális térpotenciál. Könnyebb megbecsülni, hogy milyen távolról mérhető az egyedi akciós potenciálok hatása. Az első fejezet végén becslést adok arra, hogy az általunk mért sejtek jeleit milyen távolságból mérte az elektróda rendszer. A multi mikroelektródákkal mérhető térpotenciálok felül áteresztő szűrő alkalmazása után az egyedi sejtaktivitások összegét mutatják. Az elektródák környezetében található sejtek akciós potenciáljai általában különböző nagyságú és lefutású potenciálhullámot hoznak létre a különböző elektródákon. Ennek két oka van, egyrészt a különböző sejtek különböző morfológiával és különböző felületi ioncsatorna sűrűség eloszlásokkal rendelkeznek, így dinamikus tulajdonságaik különböznek, másrészt az elektróda és a sejt, illetve a sejt különböző nyúlványainak relatív helyzete szintén különbözik minden egyes sejt-elektróda pár esetében. Ez a tény felvetette annak lehetőségét, hogy az eltérő jelalakokat felhasználva azonosítani lehet azokat az akciós potenciálokat, amelyek egyazon sejtből származnak. A szakirodalomban számos algoritmust közöltek, amelyek igyekszenek megtalálni az akciós potenciálok kiválogatásának és csoportosításának legjobb módszereit. E módszerek többsége felteszi, hogy a felvétel során az egyes sejtekből származó jelalakok változatlanok maradtak, a mért jelek különbözőségéért a jelekhez hozzáadódó, azokkal nem korrelált Gauss eloszlású zaj felelős. E jel szétválogatás (spike sorting) és osztályozás (clustering) olyan adatsort eredményez, mely az elektróda közelében található sejtekhez azok tüzeléseinek időpontjait rendeli hozzá. Ilyen típusú jelsorozatok számos esetben voltak statisztikai 8
16 és információelméleti analízis tárgyai, alkalmazva ezen tudományterületek fejlett matematikai eszköztárát. E megközelítés az akciós potenciált általában pillanatszerű és pontszerű jelenségnek tekinti, elhanyagolva a tüzelés finom időbeli és térbeli részleteit. A tüzelések szétválogatása azonban azt is lehetővé teszi, hogy megismerjük az akciós potenciálok finomszerkezetét. Míg a nyers adatban a zaj, illetve a különböző sejtek jeleinek keveredése elfedi e finom részleteket, addig a szétválogatás lehetővé teszi az egy sejttől származó akciós potenciálok jeleinek fázishelyes átlagolását, megtartva a sejtre jellemző finom részleteket és egyben csökkentve a zaj hatását. Az elektródánkénti fázishelyes átlagolás eredménye egy átlagos tüzelés elektromos terének alakulása térben és időben. A korrelálatlan zaj kiátlagolódása megbízhatóan azonosíthatóvá teszi még az igen finom részleteket is. Természetes módon feltehető, hogy az átlagolt tér-idő potenciál függvény tulajdonságai sok szempontból jellemzőek az azt létrehozó téridőbeli áramforrás eloszlásra, azaz a mért potenciál információt hordoz a forrásairól. Ismereteim szerint ezidáig nem volt ismeretes olyan módszer, amely hozzáférhetővé tette volna ezt az információt. Munkám célja egy olyan módszer kidolgozása volt, amely felhasználva egy sejt környezetében multi mikro-elektróda rendszerekkel mért elektromos potenciált, minél több információt szolgáltat annak forrásáról A direkt és az inverz probléma Az idegi ingerület vezetés során fellépő elektromos áramok változásainak sebessége alacsonynak tekinthető mind a jellegzetes agyi méret tartományokhoz, mind az elektromágneses csatolás erősségéhez képest, így az általuk keltett elektromos mező leírásakor indokolt az egyenáramú, kvázi-sztatikus közelítés használata. Ez többek között azt is jelenti, hogy a lassan változó agyi áramok által keltett mágneses tér olyan gyengén hat kölcsön az agyszövettel, hogy az általa létrehozott elektromos tér elhanyagolható, így elhanyagolható az elektromágneses hullámok hatása is. Egyenáramú közelítésünk egyben azt is jelentette, hogy a sejtek közötti elektrolit oldat dielektromos állandójából és vezetőképességéből kép- 9
17 zett időállandó kicsi a sejtek membránjain áthaladó ionáramok jellegzetes változási sebességeihez képest, így a sejteken kívüli térben az elektromos jel gyorsan terjed, minden változás gyakorlatilag egyidejűleg következik be a mérések szempontjából fontos távolságokon. Számításaink során szintén elhanyagoltuk az idegszövet dielektromos álladójának és a vezetőképességének frekvenciafüggését is. Egyszerűsítéseink eredményeképpen a sejtek membránján ki illetve befolyó áramok által keltett elektromos potenciál leírható Maxwell első törvényének és Ohm törvényének felhasználásával [Malmivuo és Plonsey, 1995]: 2 V (x, y, z) = 4πI(x, y, z) ɛ r σ (1.1) CGS rendszerben, ahol V (x, y, z) jelöli az elektromos potenciál három dimenziós eloszlását, I(x, y, z) a szintén három dimenziós áramforrás sűrűség eloszlást, ɛ r a közeg relatív dielektromos álladóját, σ a sejtek közötti folyadék vezetőképességét végül 2 háromdimenziós második derivált Laplace operatorát. Megállapíthatjuk, hogy ez az egyenlet teljes mértékben analóg az elektrosztatika alapegyenletével a Poisson-egyenlettel, a különbség az együttható értékén kívül mindössze annyi, hogy az egyenlet jobb oldalán a forrás tagban az áramforrás sűrűség eloszlás helyettesíti a töltéssűrűség eloszlást. Az egyenlet felírásakor a közeget elektromos szempontból homogénnek és irányfüggetlennek, izotropnak tekintettük. A nagyagyi szürkeállomány természetesen nem izotrop, de több vizsgálat tanúsága szerint anizotrópiája elektromos szempontból elhanyagolható [Mitzdorf, 1985]. Ha adott egy térbeli áramforrás sűrűség eloszlás, a Poisson egyenlet alapján meghatározható az általa létrehozott elektromos potenciál, ez a Poisson egyenlet direkt feladata. Megoldásának egyszerű módszere a Green-függvény módszer, mely felhasználja az egyenlet linearitását. A megoldáshoz használható Green-függvény, amely megegyezik egy pontforrás terével hengerkoordinátákban felírva: V (x, d) = I 0 ɛ r σ (x x 0 ) 2 + d 2 (1.2) 10
18 Feltéve, hogy egy I 0, erősségű forrás fekszik a koordináta rendszer főtengelyén x 0 helyen. x jelöli a mérés helyét a főtengely mentén és d a mérési pont távolságát a főtengelytől. Egy adott forráseloszlás tere megkapható a forráseloszlás függvény és a pontforrás terét jellemző Green-függvény konvolúciójával. A direkt feladat megoldása, a közeg tulajdonságainak rögzítése után, tehát nem igényel további elvi megfontolást, a potenciáltér a membránáramok ismeretében automatikusan számítható. Az inverz feladat estében adott egy potenciáltér és keressük a forráseloszlást, amely azt létrehozta. Ha a potenciált csak bizonyos mérési pontokban, vagy mérési felületen, de nem a kérdéses térész belsejében ismerjük, az inverz feladat megoldása nem egyértelmű. Ezt Helmholtz már 1853-ban megmutatta [Helmholtz, 1853]. Ezt belátni igen egyszerű: egy homogén töltött gömb potenciáltere a gömbön kívül megegyezik egy olyan ponttöltés terével, melybe összegyűjtöttük a gömbben található összes töltést. Ezért a potenciált a gömbön kívül mérve nem lehet eldönteni, hogy a teret egy végtelenül kicsi pontforrás, vagy egy véges sugarú töltött gömb hozta-e létre, illetve ez utóbbi esetben nem lehet meghatározni a gömb sugarát. Ez a példa is mutatja, hogy általános esetben nem lehet meghatározni a forráseloszlást a potenciálmérések alapján, az inverz probléma nem megoldható, illetve megoldása nem egyértelmű. Ha azonban rendelkezünk előismeretekkel a forráseloszlás tulajdonságairól, akkor ezek felhasználásával, leszűkíthető a lehetséges megoldások tere. Ha a lehetséges megoldások terét elegendően leszűkítettük, a rendelkezésre álló mérések egyértelműen kijelölik a lehetséges megoldások közül a ténylegeset. E megközelítés során az előismeretek segítségével tett megszorításokból a forrás egy modelljét építjük fel és a mérés feladata, hogy meghatározza a modell szabad paramétereinek értékeit. E modell alapú elemzés eredménye tehát az a paraméter készlet, amelyet a modellbe helyettesítve és a potenciálteret kiszámolva a lehető legnagyobb egyezést kapjuk a mért értékekkel. Ez az optimális paraméter készlet tartalmazza az új információt, amely jellemző a tényleges forrásra. Az elemzés maga egy modell illesztési folyamat. Összegezve megállapíthatjuk, hogy e módszer megmutatja, hogy a megfelelő modell nem csak a mérési eredmények magyarázatában segít, segítségével új információ nyerhető a mért adatokból. 11
19 A Poisson-egyenlet inverz feladatában tehát központi kérdés annak a megszorítás rendszernek azaz modellnek a felállítása, amely hűen tükrözi a rendszerről meglévő ismereteinket. E modellnek egyensúly kell találni a két egymásnak általában ellentmondó kívánalom között. Egyrészt elegendően egyszerűnek kell lennie, ahhoz, hogy minden paramétere meghatározható legyen a mérések alapján, más szavakkal a megszorítások legyenek elég szigorúak ahhoz, hogy biztosítsák az inverz megoldás egyértelműségét. Másrészt elegendően komplexnek kell lennie, hogy leírja a mért adatok sokféleségét, más szavakkal a megszorítások legyenek elég lazák ahhoz, hogy pontos illeszkedést tegyenek lehetővé a mért adat és a modell eredményei között A Poisson inverz probléma és az EEG/MEG alapú képalkotó eljárások A Poisson inverz probléma az alap feladata mindazon eljárásoknak, amelyek EEG vagy MEG mérések alapján akarják meghatározni az agyszövet aktivitását. Számos olyan feltételrendszer és megoldási módszer áll rendelkezésre a szakirodalomban [Baillet és mtsai, 2001], melyek biztosítják az inverz feladat megoldhatóságát, de az általuk feltételezett tulajdonságok nem felelnek meg a multi mikro elektródák által mért idegsejtek mint források tulajdonságainak, így egyik sem alkalmazható változtatás nélkül ebben az esetben. A feltételezett forrás leírható véges számú pont forrás összegeként. Egy pontforrás leírásához legkevesebb négy szabad paraméter szükséges. Figyelembe véve a kísérleti technikában alkalmazható mikroelektródák alacsony számát, ez a módszer a membrán áramok igen durva térbeli leírását teszi csak lehetővé. Finomabb felbontás érhető el a szorosan vett képalkotó (EEG/MEG imaging) eljárásokkal. Ezek az eljárások több rögzített térelemre, voxelre bontják a képet, mint a mérési pontok száma. Hogy mégis biztosítani tudják a forrás kép egyértelműségét, globális kényszerfeltételeket alkalmaznak. A voxelek térbeli rögzítése lehetővé teszi, hogy a feladatot egy lineáris egyenletrendszerként fogalmazzuk meg. Ha a voxelek száma nagyobb, mint a mérési pontok száma, az egyenletrendszer alul- 12
20 határozott, végtelen sok megoldása egy eltolt lineáris alteret, azaz egy affin teret feszít ki a voxelek aktivitásai által meghatározott sok dimenziós forrástérben. Az alkalmazott globális feltétel feladata, hogy a végtelen sok forráseloszlás közül, amelyek mind kielégítik az adott egyenletrendszert, azaz mind ugyan azt a mért potenciált eredményezik, kiválassza azt amelyiket a probléma valódi megoldásának tekintünk. Több lehetséges kényszerfeltétel róható ki a forrásképre, megkövetelhető, hogy legyen a lehető legkisebb a forráskép normája, legyen a lehető legsimább a forráskép (LORETA módszer, Low REsolution TomogrAphy), szintén megkövetelhető, hogy legyen a lehető legritkább a forráskép, vagy feleljen meg bizonyos anatómiai feltételeknek. A fenti kényszerfeltétel rendszerek egyike sem írja le megfelelően a mi kísérleti elrendezésünket. A minimum norma feltétel csak 2 dimenziós esetben ad kielégítő eredményt. Ez megfelelő közelítés lehet, ha az agykérgi aktivitást vizsgáljuk, de nem megfelelő esetünkben, hiszen a sejtek 3 dimenzióban helyezkednek el. A széles körben használt LO- RETA módszer ugyan jó eredményeket ad 3 dimenziós forrás eloszlásra is, de feltételezi a forráseloszlás simaságát. Ez a feltételezése nem áll összhangban azzal, hogy az akciós potenciál általában igen kis térrészben keletkezik az axon dombon illetve az axon kezdeti szakaszán, éles csúcsot alkotván a forrásképben. A forráskép ritkasága jól leírná az akciós potenciál során folyó fő áramot amely az axon kezdeti szakaszán folyik a sejtbe befelé, ám, mint látni fogjuk, a tüzelés elektromos terének kialakításában szerepe van a sejtmembrán összes többi részén folyó áramoknak, és a ritkasági feltételezés nem illeszthető össze a dendritikus membrán folytonosságával. Az akciós potenciálok elektromos terének leírásárhoz szükséges volt egy új feltétel rendszer bevezetése. Ellentétben az EEG felvételeknél használt skalpra helyezett makro elektródákkal, az agyszövetbe szúrt mikroelektródák szövetkárosító hatása következtében egészen ritka az olyan kísérleti elrendezés, amelyben a mérési pontok körülölelnek egy zárt térfogatot. Ennek hiányában rögzített térelem rendszer nem alkalmazható, a források távolsága ismeretlen paraméterré válik, amely nem lineárisan befolyásolja a mért potenciál képet. E nemlineáris hatás azt eredményezi, hogy a feladat nem fogalmazható meg lineáris egyenletrendszer 13
21 formájában, így a nem csak a fenti módszereknél megfogalmazott feltétel rendszerek, de az alkalmazott megoldási eljárások sem alkalmazhatóak esetünkben A monopólus modell Keressük tehát az idegsejt lehető legegyszerűbb modelljét, amely az éppen akciós potenciált létrehozó sejtet mint áramforrást a mérésekkel összhangban képes leírni. Keresésünk ezért a legegyszerűbb modellek felől indul és addig növeljük az alkalmazott modell részletgazdagságát, amíg az a képessé nem válik a mér adatok leírására. A legegyszerűbb forrás leírás a monopólus modell. A szakirodalomban a tüzelő sejtet többször tekintik monopólus áramforrásnak [Gray és mtsai, 1995, Jog és mtsai, 2002, Chelaru és Jog, 2005]. A monopólus tér gömbszimmetrikus és a távolsággal fordított arányban csökken. A monopólus tér akkor is jó közelítést adhat, ha a forrás nem gömbszimmetrikus. Ennek két feltétele van: egyrészt szükséges, hogy a forrás által kibocsájtott illetve elnyelt áramok mennyisége különbözzön, előjeles összegük ne nullát adjon, másrészt, hogy a forrás kiterjedése kicsi legyen a megfigyelési távolsághoz képest. E feltételek teljesülése számos tényező függvénye, függ a sejt morfológiájától, élettani tulajdonságaitól, a sejt és az elektróda viszonylagos helyzetétől is. A monopólus közelítésen alapul a sejt helyzetének meghatározása háromszögeléssel, tetródokkal végzett mérések alapján [Jog és mtsai, 2002, Chelaru és Jog, 2005]. E módszer feltételezi, hogy a tüzelő sejtek tere jól közelíthető egy monopólus térrel, tudomásom szerint azonban nem készült ez ideig olyan munka, amely megvizsgálta volna, e közelítés helyességét és alkalmazhatóságát. Ezért munkám első lépése a monopólus közelítés helyességének vizsgálata volt. Egy monopólus forrás modellnek négy szabad paramétere van, három koordináta és egy forráserősség paraméter, így paramétereit négy, nem egy síkban fekvő pontban mért potenciál alapján lehet meghatározni. Az általunk alkalmazott multi mikroelektróda 16, egy egyenes mentén fekvő mérési pontot biztosít. Ez a elektróda elrendezés nem tesz le- 14
22 hetővé teljes háromdimenziós helymeghatározást, meghatározatlanul hagyja a szöget ami alatt a sejt látszik, azonban az elektróda többlet lehetővé tette a monopólus és egyéb pontforrás közelítések pontosságának ellenőrzését Módszerek In vivo mérések Az idegsejtek elektromos jeleit macskák elsődleges hallókérgébe ültetett 16 csatornás mikroelektróda rendszerrel mértük. A beültetés pentobarbitállal altatott (40 mg/kg i.p.) állatokba történt, a felvételek azonban már éber állapotban készültek. A 16 mérési pont az agyfelszínre merőleges vonalban helyezkedett el. Az első csatorna 400 µm távolságban a felszíntől, a 2-es és 3-as réteg határának közelében volt, míg a további mérési pontok 100 mikrononként követték egymást, 1900 µm agykérgi mélységig a 6-os réteg határának közelébe. Az elektróda egyaránt mért spontán és hangingerrel kiváltott jeleket. A mért jelek az előerősítés után egy szélessávú sávszűrőn haladtak át, melynek alsó határfrekvenciája 300 Hz míg felső határfrekvenciája 5 khz volt. A szűrt jeleket 20 khz frekvenciával mintavételeztük és 12 bit pontossággal alakítottuk digitális jelekké, melyeket a számítógépen eltárultunk. A mérő rendszer részletes leírása megjelent Ulbert és mtsai [2001] közleményében. Az akciós potenciálokat a Spike-O-Matic nevű szabadon hozzáférhető programmal gyűjtöttem össze és osztályoztam [Pouzat és mtsai, 2002]. Az osztályozó program a jelalakok hasonlósága alapján 16 osztályba gyűjtötte össze az akciós potenciálokat. A jelalakok vizsgálata alapján 2 osztály több sejt jeleinek összegének, egy jel osztály pedig egy alacsony amplitúdójú akciós potenciál és egy lassabb potenciál hullám összegének bizonyult. E a három osztályt elhagytam a további elemzések során. A megmaradt 13 jelosztály jeleit minden csatornán minden időpillanatban átlagoltam, ilyen módon előállt az a 13 téridőbeli potenciálmintázat, amely a további elemzések alapját képezte. Minden, a kísérleti állatokat érintő munkát az SFN ajánlásival összhangban az MTA 15
23 Monopólus forrásmodel Potenciál 0 Dipólus forrásmodell Potenciál + Agykérgi mélység Agykérgi mélység A B Kvadrupólus Potenciál forrásmodell + Ellenáram modell Elektróda Agykérgi mélység, x Agykérgi mélység C Nyelõ D sejt elektróda távolság, d Forrás 1.1. ábra. Az alapvető áramforrás modellek szerkezete. A: Egy negatív monopólus forrás (nyelő) gömbszimmetrikus, mindenhol negatív potenciát hoz létre. B: A dipólus modell egymáshoz közeli forrás nyelő párt ír le, és kétfázisú potenciálteret hoz létre. C: kvadrupólusl modell egy központi nyelőt ír le, amelyet két szimmetrikus forrás egyenlít ki, és háromfázisú potenciálteret hoz létre. D: Az ellenáram modell egy vonalforrást ír le, amely hengerszimmetrikus potenciálteret hoz létre. Feltételezi, hogy a vonalforrás párhuzamos az elektródával, valamint csak egy pontszerű negatív nyelő található rajta és pozitív források mindenhol máshol. 16
24 Pszichológiai Kutatóintézet Etikai Bizottságának engedélye alapján végeztünk Számítógépes szimulációk Az akciós potenciál megjelenését egy egyszerűsített morfológiájú 264 rekeszből felépített idegsejt modellen modelleztük. A láncszerűen összekapcsolt rekeszek mindegyike 5 µm hosszú volt. Az ekvipotenciálisnak tekintett rekeszek membránpotenciáljának alakulását a Hodgkin-Huxley formalizmust követő csatolt parciális differenciálegyenlet rendszerrel írtuk le. A differenciálegyenlet rendszer felírását és integrálását a Neuron programcsomaggal végeztük [Hines, 1989], amely egy szabadon hozzáférhető, magas szintű, objektum orientált programozási környezet idegsejtek és azok hálózatainak számítógépes szimulációjához. Az ioncsatornák kapuváltozóinak kinetikai paramétereit Mainen és Sejnowski [1996] cikke alapján állítottuk be. A csatornák felszíni sűrűségénél is a fenti cikket vettük alapul, azonban a nátrium és kálium csatornák sűrűségét jelenősen lecsökkentettük a sejttesten és az axonon hogy a sejt által létrehozott akciós potenciál nagysága a sejten kívüli térben illetve folyadékban megfeleljen az általánosan ismert mérhető amplitúdóknak. Az egyes ioncsatorna típusok által elérhető legnagyobb vezetőképesség értékeit az 1.1. táblázat tartalmazza. Az akciós potenciált a sejttestbe vezetett depolarizáló árammal váltottuk ki, melynek időbeli lefutását egy alfa függvény írta le. A befecskendezett áram nagyságát úgy állítottuk be, hogy kicsivel haladja meg az akciós potenciál kiváltásához feltétlenül szükséges küszöb értéket, így a sejten létrejött téridőbeli árameloszlás kevéssé a kiváltó áramokat, inkább az akciós potenciál belső dinamikáját tükrözze. Az élő szövetben a sejteken kívüli illetve sejtek közötti teret ionok vizes oldata tölti ki. Elektromos szempontból ez híg elektrolit, mely térvezetőként vezeti tovább a befecskendezett áramot. Híg elektrolit oldatokban az Ohm-törvény jó közelítéssel érvényes, és ezt behelyettesítve az elektrosztatikát leíró első Maxwell egyenletbe azt kapjuk, hogy a potenciál épp úgy a Poisson egyenletet elégíti ki, mint az elektrosztatikában [Malmivuo és 17
25 Sejtrészek Axon Sejttest Dendrit Hossz [µm] Átmérő [µm] C m [µf/cm 2 ] R a [Ωcm] g l [S/cm 2 ] 3e-5 3e-5 3e-5 g Na [ps/µm 2 ] g Kv [ps/µm 2 ] g Km [ps/µm 2 ] g KCa [ps/µm 2 ] g Ca [ps/µm 2 ] V e [mv ] táblázat. A szimulált idegsejt modell paraméterei. Plonsey, 1995]: 2 V EC (x, y, z) = 4πI(x, y, z) σ (1.3) A fenti, CGS rendszerben felírt egyenletben V EC (x, y, z) jelöli a potenciál eloszlását a térvezetőben, I(x, y, z) az áram forrás sűrűség térbeli eloszlását, σ az elektrolit vezetőképességét és 2 a térbeli második deriváltat azaz a Laplace operátort. A különbség az elektrosztatika alapegyenletéhez képest mindössze annyi hogy a jobb oldalon a töltéssűrűség helyén az áramforrás sűrűség szerepel, illetve az együtthatókban a közeg permeábilitása mellett megjelenik a közeg vezetőképessége is. Az áramforrás sűrűség egyaránt felvehet pozitív értéket, ami a sejtek közötti térbe befecskendezett pozitív áramot vagy az onnan elvezetett negatív áramot jelenti, ezt szűkebb értelembe vett forrásnak nevezzük, illetve negatív értéket, amely a térvezetőből elvezetett pozitív, vagy oda befecskendezett negatív töltéseket jelez és nyelőnek nevezzük. Mivel a sejtek kettős lipid membránja igen jó szigetelő, a sejtből ki, illetve az oda be áramló ionok, a sejtek közöttik térben forrásként illetve nyelőként jelennek meg. A akciós potenciál szimulációja során a membránpotenciál és az egyes csatornák vezetőképességének pillanatnyi értékéből minden egyes rekesz esetében kiszámoltuk a membránon áthaladó összes áramot (Im), j majd ez alapján, a Green-függvény módszer követve 18
26 meghatároztuk a teljes sejt által keltett elektromos potenciálteret: V EC (x) = 1 σ n j=1 I j m (x j x) 2 + d 2 j (1.4) Ahol minden egyes rekeszt pontszerű áramforrásnak tekintettünk. Feltételeztük, hogy az elektróda az x koordináta mentén fekszik és itt méri a V EC (x) egy dimenziós potenciál eloszlást. x j jelöli a j-edik rekesz x tengely menti pozícióját, d j az x tengelytől mért távolságát. Az összegzés pedig végigfut a sejt összes rekeszén (n). A sejtek közötti teret homogén és izotrop közegnek tekintettük, melynek vezetőképessége 1/300 S/cm [Varona és mtsai, 2000]. A sejtek közötti tér dielektromos tulajdonságait frekvenciafüggetlennek tekintettük, az elektromos jel forrás és elektróda közötti terjedéséhez szükséges időt pedig elhanyagolhatónak. Ezek alapján kiszámítottuk az elektromos teret a sejttel párhuzamos egyenes mentén, 10-től 200 µm távolságra a sejttől, 5 µm-es lépésekben és eltároltuk 40 khz mintavételezési frekvenciával Modell illesztés A rögzített és osztályozott akciós potenciálok osztályátlagaiból csak a legnagyobb abszolút potenciál idő pillanatában mért térbeli potenciál eloszlást tettem a modell illesztés alapjává, mivel a legnagyobb amplitúdó biztosította a legnagyobb jel/zaj arányt. A legnagyobb abszolút potenciál minden esetben negatív volt, ezért illesztés előtt -1-re normáltam a mért térbeli potenciál mintázatokat (TPM), Ezt a szabályt követve, szintén -1-re normáltam a szimuláció eredményeképpen kapott TPM-okat is. A modellek illesztése egy hibafüggvény minimumának a meghatározása az általában sok dimenziós paramétertérben. A hibafüggvény minden esetben az illesztendő modell által létrehozott TPM és a mért vagy szimulált TPM euklideszi távolsága volt. Mivel az illesztendő modellek és a hibafüggvények a távolság paraméter nemlineáris függvényei voltak, illesztésüket analitikusan elvégezni nem lehetett, a hibafüggvények minimum helyeit numerikus szélsőérték kereső algoritmusokkal határoztam meg. A szimulált adatokra 19
27 illesztés alapján a kvázi-newton algoritmus jobb eredményeket adott, mint a konjugált gradiensek módszere, így az értekezésemben bemutatott eredmények kvázi-newton módszerrel készültek. A modellek illesztésre és minden egyéb numerikus elemzésre a Scilab szabadon hozzáférhető tudományos programcsomagot használtam [Gomez, 1999]. Az illesztett monopólus modell a következő volt: V m EC(x) = I m σ((x 0 x) 2 + d 2 0) 1/2 (1.5) Ennek szabad paraméterei, melyeket a mért adathoz illesztve meghatároztunk: a forrás erőssége I m, a forrás helyzete az elektróda mentén x 0 és a forrás távolsága az elektróda egyenesétől d 0. A numerikus minimum kereső algoritmus egy kezdeti értéktől indulva lépésenként közelíti meg a hibafüggvény helyi minimumát, ezért a modell minden egyes szabad paraméterének olyan kezdeti értéket kellett választani, amely lehetőség szerint közel esik a hibafüggvény valódi minimumához. Az x 0 koordináta esetében természetes választás volt, az észlelt TPM negatív csúcsának elektróda menti helyzetét tenni a forrás hasonló paraméterének kezdeti értékévé. A d 0 távolság esetében nem volt ilyen természetes választás, de a szimulációs kísérletek tanúsága szerint a 60 µm-es távolság megfelelő kiindulási helyzetet jelentett a 10-től 200 µm-ig terjedő távolságban, amely tartomány Henze és mtsai [2000] szerint felöleli a lehetséges megfigyelési távolságokat. Mivel az illesztés előtt a TMP-okat normáltuk, a forráserősség kezdeti értéke a kezdeti távolság inverze volt: I m = 1/d 0. A háromfázisú kvadrupólusl forrásmodell által létrehozott potenciál: V q EC (x) = Iq (d 2 0 2(x 0 x) 2 ) σ((x 0 x) 2 + d 2 0) 5/2 (1.6) A szabad paraméterek és a kezdeti értékek megegyeztek a monopólus esettel. Az általános harmadrendű pontforrásmodell egy monopólus, egy dipólus és egy kvad- 20
28 rupólusl tag lineáris kombinációjaként állt elő: V EC (x) = I m σ((x 0 x) 2 + d 2 0) 1/2 + 2I d (x 0 x) σ((x 0 x) 2 + d 2 0) 3/2 + Iq (d 2 0 2(x 0 x) 2 ) σ((x 0 x) 2 + d 2 0) 5/2 (1.7) Ennek a modellnek öt szabad paramétere volt: I m, I d, I q, d 0, x 0. A kezdeti értékek megegyeztek a monopólus esettel a két téri paraméter, x 0, d 0, és a monopólus forráserősség I m esetében, illetve két új taggal egészültek ki, a forrás erősségek esetében I d = I q = I m /10. Az ellenáram modellt egy negatív pontforrás és egy pozitív vonalforrás eloszlás összegekét határoztam meg. Feltételeztem, hogy a vonalforrás párhuzamos a mérő elektródával, melynek helyzetét képleteimben az x koordináta jelöli. A numerikus illesztéshez a vonalforrás eloszlást véges hosszúságú vonalforrás szakaszok láncára bontottam, ahol az egyes szakaszokon belül a vonal menti forráserősség álladó volt. A véges hosszúságú vonalforrás szakasz által létrehozott elektromos potenciált Holt és Koch [1999] képlete alapján számítottam ki. Összegezve az ellenáram modellt egy negatív pontforrás és N db pozitív vonalforrás lineáris kombinációjaként írtam fel: V EC (x) = I 0 σ (x 0 x) 2 + d N I j σ Log (x j+1 x) 2 + d 2 0 (x j+1 x) (1.8) (x j x) 2 + d 2 0 (x j x) j=1 Ahol I 0 < 0 a negatív pontforrás erőssége, I j 0 a j-edik pozitív vonalforrás szakasz erőssége, amely szakaszt a x j és az x j+1 pontok határolnak. Az x j=1...n+1 végpontokat egyenletesen osztottam el az elektróda mentén és helyzetük nem változott az illesztés során. A modell szabad paraméterei a következők: x 0, d 0, I 0 és I 1...N. N=12 áramforrás szakaszt 21
29 használtam a 16 csatornás mért illetve szimulált TPM-ok illesztésére. Sok dimenziós paramétertérben jelentős kérdés a megfelelő kezdeti érték kiválasztása. Ezért előzetes számításokat végeztem, hogy közelebb kerüljek a paraméterek legmegfelelőbb értékeihez. A mért TPM-ra egy monopólus modellt illesztettem, melyet megszorítottam oly módon, hogy az általa előállított potenciál minden pontban kisebb vagy egyenlő legyen mint a mért TPM. E megszorított monopólus modell paramétereinek kezdeti értékei megegyeztek a monopólus modell illesztésénél használtakkal. A legjobb illeszkedést eredményező paraméter készlet, illetve az általa létrehozott potenciál szolgált kiindulásként az ellenáram modell illesztésekor. A megszorított monopólus illesztésekor kialakult x 0 paraméter tettem az ellenáram modell megfelelő paraméterének kezdeti értékévé. Az I 1...N áramforrás erősségek kezdeti értékeit egyenletesen ugyan azon értékre állítottam be úgy, hogy az általuk létrehozott egyenletes térbeli eloszlású pozitív potenciál 60 µm távolságból egyenlő legyen a megszorított monopólus modell által létrehozott TPM és a mért TPM különbségének pontonkénti átlagával. A d 0 távolság paraméter kezdeti értéke ismét 60 µm volt. A mért és a modell által létrehozott potenciálok legjobb illeszkedését eredményező paraméter készlet becsléként szolgál a források valódi jellemzőire. Ilyen módon az illesztett d 0 paraméter becslést szolgáltat a forrás távolságára, az illesztett I 0 és I 1...N forrás erősségek pedig becslést adnak a sejt membránján ki illetve az oda befolyó ionáramok nagyságára illetve azok térbeli eloszlására. A teljes áramforrás sűrűség (current source density, CSD) eloszlás becsléséhez a pontforrás I 0 áramát a szakasz hosszával elosztva hozzáadtam a megfelelő vonalforrás szakasz áramforrás sűrűségéhez. Az ellenáram modell illesztése így új módszert szolgáltat a sejtek áramforrás sűrűségének becslésére. Az általunk kapott áramforrás eloszlásokat összehasonlítottam a hagyományos módon kiszámolt egy dimenziós CSD eloszlással. A hagyományos CSD eloszlásokat a következő egyenlet alapján számítottam ki [Nicholson és Freeman, 1975]: I(x) = σ V EC(x + dx) 2V EC (x) + V EC (x dx) dx 2 (1.9) 22
30 Ahol σ jelöli a sejtek közötti folyadék vezetőképességét és dx a mérési pontok egymástól mért távolságát, amely esetünkben 100 µm volt Eredmények A monopólus modell illeszkedésének vizsgálata in vivo mért adatokra Az akciós potenciálok által a sejten kívüli térben létrehozott elektromos potenciálhullám téridő mintázatait -kialakult szakmai elnevezés hiányában- a továbbiakban mikro-mezőpotenciáloknak nevezem. Az in vivo mért akciós potenciálok osztályozása és az osztályok elemeinek átlagolása után megkaptam a mikro-mezőpotenciálok tipikus téridő mintázatait (1.2.ábra). Alacsony frekvenciás közelítésben a tér és az idő szétválasztható, így a mikro-mezőpotenciálokat, térbeli potenciál mintázatok (TPM) sorozatának tekintettem. A pontforrás közelítések illeszkedését minden egyes osztály esetében a legnagyobb negatív potenciál csúccsal rendelkező TPM-on vizsgáltam (1.3. ábra). A mért átlagos TPM-ok jelentős hasonlóságot mutatnak negatív monopólus források teréhez (1.3. ábra). Az első lépés annak vizsgálatában, hogy e mintázatokat valóban monopólus források hozták-e létre vagy sem a bennük előforduló pozitív potenciálértékek szignifikanciájának meghatározása volt. Ha e TPM-okat negatív monopólus források hozták létre, a bennük előforduló pozitív értékek nem lehetnek nagyobbak mint amit a mérési zaj létrehozhatott. Ahogy azt az 1.2. táblázat mutatja, minden vizsgált TPM-ban előfordult pozitív potenciál érték. Az esetek többségében a maximum és a minimum aránya Q = V max EC és -2% között volt. A mért V max EC csúcs nagyságával, Q=-53%. /V min EC -1% érték egyetlen esetben (C) volt összemérhető a negatív Minden egyes átlagolt TPM minden egyes csatornáján meghatároztam a mért potenciál 23
31 A B C D E F G H I J K L M 0.1 mv 1 ms 1.2. ábra. Az azonosított 13 akciós potenciál osztály átlagos hullámformái, 16 csatornán. A csatornák közötti távolság 100 µm volt. Az egyes hullámok egy 2.5 ms hosszú időtartamot mutatnak. EC potenciál [µv] A B C D G H -140 E F Agykérgi mélység [mm] I K J L M 1.3. ábra. A tüzelés osztályok (A-M) átlagolt térbeli potenciál mintázatai (TPM) az agykérgi mélység függvényében, a legnagyobb (negatív) potenciál csúcs időpillanatában. 24
32 Sejt A B C D E F G H I J K L M V min EC in µv V max EC , in µv Q % ban 53.8 N N táblázat. A TPM-ok tulajdonságai: VEC min max a tüzelés amplitúdója, VEC a potenciál maximuma ugyanebben az időpillanatban. Q = VEC max min /VEC. N + és N jelöli azon csatornák számát, amelyeken VEC min időpillanatában a potenciál szignifikánsan pozitívabb, vagy negatívabb volt, mint az a zaj alapján várható lett volna. α = 1% szignifikancia szinten értékekhez tartozó konfidencia intervallumot. Az idegrendszeri zaj általában nem követi a Gauss eloszlást [Dimitrov, 2002]. A mért potenciálok eloszlása a mi esetünkben is szignifikánsan különbözött a Gauss eloszlástól. Ennek oka valószínűleg az, hogy a közeli akciós potenciálok jelei a zajhoz adódva növelik a magasabb abszolút értékű mérések arányát. Mindazonáltal, a központi határeloszlás tétel alapján megállapíthatjuk, hogy a nem Gauss eloszlású V EC valószínűségi változókból n mintavételből számolt M(V EC ) átlag eloszlása nagy n mintaelemszám esetén tart a Gauss eloszláshoz, így a hozzá tartozó konfidencia intervallum jól közelíthető a [ M(V EC ) ad(v EC), M(V EC ) + ad(v ] EC) n n (1.10) tartománnyal, 2Φ(a) 1 szignifikancia szinten, ahol D(V EC ) jelöli az adott csatorna jeleinek szórását a tüzelés adott fázisában az n tüzelést tartalmazó osztályban, Φ pedig a standard normális eloszlásfüggvényt. Az n mintaelemszám a legkisebb elemszámú osztályban is 300 fölött volt, ez pedig bőven elég ahhoz, hogy a csatornánkénti osztályátlagot normális eloszlásúnak tekinthessük. A potenciál negatív csúcsával egy időben mért V EC értékeket akkor tekintettem szignifikánsan nem nulla értékűnek ha a nulla potenciál nem volt eleme az 1%-os szignifikanciaszinthez tartozó konfidencia intervallumnak. Minden egyes osztályátlagban találtam olyan 25
33 csatornát, amelyen a tüzelés negatív csúcsával egyidőben mért potenciál szignifikánsan pozitív volt. Az 1.2. táblázat tartalmazza azoknak a csatornáknak a számát, amelyeken a mért potenciál szignifikánsan pozitívabb (N + ) vagy negatívabb (N ) volt mint az a zajhoz alapján várható lett volna, 1%-os szignifikancia szinten. Adataink azt mutatták, hogy a potenciál tipikusan a negatív csúcsától számított µm elektróda menti távolságban elérte a nulla illetve nullától nem szignifikánsan különböző értékeket. Figyelembe véve az agykéreg és a hippokampusz közti különbségeket, illetve az potenciál alakulása közötti lehetséges különbségeket az apikális-bazális tengely és az arra merőleges irány mentén, ez az eredmény nem mond ellent Henze és mtsai [2000] eredményeinek, akik azt találták, hogy tüzelések mikro-mezőpotenciálja zajszintre csökken körülbelül 150 µm-es távolságban a sejttől. Lényeges különbség azonban, hogy a mi adatainkban a potenciál növekedése sok esetben nem állt meg a zajszinten, hanem tovább növekedve pozitív értékeket is elért, ahogy a távolság nőtt Általános pontforrás modellek illeszkedésének vizsgálata in vivo mért adatokra A szignifikánsan pozitív potenciál értékek jelenléte cáfolta a feltételezést, hogy a mért TPM-okat monopólus források hozták létre, de nem zárta ki a lehetőséget, hogy a mért eloszlások forrásai leírhatóak illetve megfelelően közelíthetőek bonyolultabb pontforrás modellekkel. Ennek vizsgálatához három pontforrás modellt illesztettünk numerikusan, a mért TPM-okra: egy monopólus, egy kvadrupólus és egy általános harmadrendű pontforrásmodellt, amely a multipólus sorfejtés első három tagjának figyelembevételével, egy monopólus, egy dipólus és egy kvadrupólus tag lineáris kombinációjakét állt elő. Az illeszkedések illetve eltérések vizsgálatához, mind a mért TPM-okat, mind a rájuk egyenként illesztett modellek által létrehozott TPM-okat negatív csúcsaik egybeejtésével összeillesztettük és pontonként átlagoltuk a 13 tüzelés osztályra, ilyen módon a potenciálok illetve 26
34 Normált potenciál mért monopólus Normált potenciál mért kvadrupólus A Normált potenciál C Távolság [mm] 0-1 mért mono+di+ kvadrupólus Távolság [mm] B Hiba D Távolság [mm] monopólus kvadrupólus mono+di+ kvadrupólus Távolság [mm] 1.4. ábra. A, B, C, szaggatott vonal: A normált 13 TPM csúcsainak egymásra illesztésével és átlagolásával kapott átlagos térbeli potenciál eloszlás, a csúcstól mért távolság függvényében. Folytonos vonal: az illesztett modellek által létrehozott TPM-ok hasonló módon egymáshoz illesztett átlaga. A: monopólus modell, B: quardupólus modell. C: általános harmadrendű pontforrás modell, ami egy monopólus, egy dipólus és egy kvadrupólusl tag lineáris kombinációja. D: Az illesztési hiba átlagának és a hozzá tartozó szignifikancia intervallumnak térbeli eloszlása a három pontforrás modell esetében. eltérések átlagos távolságfüggését vizsgálhattuk (1.4. ábra). A monopólus modellek kisebb illesztési hibát eredményeztek, mint a kvadrupólus modellek, azaz megállapíthatjuk, hogy a mért TPM-ok közelebb voltak a monopólus térhez, mint a kvadrupóluslhoz, de jelentős eltérést is mutattak mindkét modelltől. A monopólus modellek potenciáltere szignifikánsan alulbecsüli a mért potenciált a negatív csúcs környezetében, míg a kvadrupólusl modellek tere túlbecsüli azt. Az illesztési hiba az általános harmadrendű pontforrásmodell esetében volt a legkisebb, azonban ugyan abban a nagyságrendben maradt, mint az előző két esetben. Megfigyelhető, hogy a becslési hiba nagysága egyik esetben sem egyenletesen oszlik el a távolság függvényében (1.4. D ábra). Ez arra utal, hogy a hibát nem a mérési zaj okozta, hanem az illesztésre használt függvények alakja 27
35 nem volt megfelelő a mért mintázatok leírásához, a modellek paramétereinek állításával nem lehetett a mért eloszlásokat kielégítően megközelíteni. Ugyan erre utal az is, hogy a forrás távolságát - amely mindhárom esetben az illesztett modellek szabad paramétere volt - az illesztés minden esetben valószínűtlenül kicsiny értékre állította be, értéke elérte a 10 5 mikrométeres nagyságrendet. A mért Q arányok és az illesztési hibák megmutatták, hogy a mért eloszlások közel vannak a negatív monopólus térhez, azonban a kicsiny de szignifikáns pozitív potenciálok jelenléte illetve az illesztési hibák nem egyenletes távolságfüggése bebizonyította, hogy a mért potenciál mintázatokat nem hozhatták létre monopólus források. A negatív Q arányok azt eredményezik, hogy a háromszögelés módszere nem alkalmazható ezekben az esetekben a forrás távolságának becslésére. A monopólus modell által becsült valószerűtlenül kicsiny forrástávolság azt mutatta, hogy a mért TPM-ok keskenyebbek, mint amit a monopólus modell létrehozhatott, bármely paraméter beállítással. A pontforrásmodell kiterjesztése a dipólus és a kvadrupólusl tagokkal nem szüntette meg a mért és az illesztett potenciál eloszlások közti szignifikáns eltéréseket illetve az eltérésekben észlelt jellegzetes térbeli mintázatot. Összefoglalva megállapíthatjuk, hogy a pontforrás modellek nem illeszkedtek megfelelően a mért TPM-okhoz, az észlelt jelenségek leírása új modellkeretet igényelt Az ellenáram modell felépítése Az ellenáram modell lényegi újdonsága a pontforrás modellekhez képest az, hogy valódi térbeli kiterjedéssel rendelkezik, ugyanakkor megtartja az egyszerűbb modellek azon tulajdonságát, hogy paraméterei meghatározhatóak a mért TPM-ok alapján. Hogy ezt elérjem, a következő megszorításokat tettem: a modellt egy dimenzióba szűkítettem le, mivel a leírandó mérések is egy tengely mentén történtek. Megkívántam, hogy ez az egy dimenziós áram forrás eloszlás, azaz vonalforrás párhuzamos legyen a mérés tengelyével. Ez a kívánalom jól egyezik a piramis sejtek dendritfájának hosszúkás morfológiájával és agy- 28
36 kérgi elhelyezkedésével, mivel az elektróda az agyfelszínre merőlegesen, tehát a piramis sejtek apikális dendritjeivel párhuzamosan helyezkedett el. Még egy fontos megszorítást tettem, hogy az inverz feladat megoldható legyen: megkívántam, hogy a vonalforrás egy negatív monopólus pontforrás és egy pozitív vonalforrás eloszlás összegeként álljon elő. Így a modell feltételezi, hogy a sejt felszíni áramforrás rendszert egyetlen jelentős nyelő jellemzi, amely ismeretlen térbeli eloszlású, de pozitív ellenáramokat indít a sejt egész felszínén. Azonban nem kívántam meg, hogy a sejtből ki illetve az oda befolyó áramok előjeles összege nulla legyen. Az ellenáram modell paramétereinek száma önkényesen választható 4 és a mérési pontok száma között, ami jelen esetben 16 volt. Mivel a paraméterek számával nőt az az információ amit e módszer alkalmazásával a sejtről szerezhetünk, ezért a paraméterek számát a lehetséges maximum közelében választottam meg, 15 paramétert használtam a 16 csatornás mért illetve szimulált jel leírására. A paraméterek számával ugyancsak nőt a szükséges számítási idő is ezért a 64 csatornás szimulált adatsor leírására csak 35 paramétert használtam. Ilyen nagy számú paraméterrel még a fenti megszorítások mellett is igen nagy szabadságot kapunk, és a modell jól illeszthető számos különböző TPM-ra, mégsem lehet azonban bármilyen eloszlást leírni e modellel. Például egy olyan eloszlás, amelynek két egyenlő negatív csúcsa van, nem írható le az ellenáram modellel Az ellenáram modell vizsgálata szimulált adatokon Az akciós potenciál létrejöttét egy ioncsatorna alapú, Hodgkin-Huxley formalizmust követő, sokrekeszes modellel szimuláltuk, amely a Mainen és Sejnowski [1996] által felépített, neokortikális ötödik rétegbeli piramis sejtmodell egyszerűsített változata volt. A sejt tüzelését a sejttestbe vezetett árammal váltottuk ki, melynek időbeli lefutását egy, a szinaptikus áramok leírására gyakran használt függvény, az alfa függvény írta le. Az ingerlő áram megindítása után 0.39 ms-al, egy 0.18 ms hosszú idő intervallum kezdődött, amikor a sejtmembránon átfolyó áram rendszert egy kis kiterjedésű nyelő jelle- 29
37 0.6 Agykérgi mélység [mm] A EC potenciál [µv] B Hiba Idõ [ms] Idõ [ms] CCM illesztés monopólus illesztés C Idõ [ms] 1.5. ábra. A: A membránáram előjelének téridő térképe a szimulált akciós potenciál során. Fekete szin jelőli a negatív áramot, fehér a pozitívat, szürke pedig azokat az áramokat, amelyek abszolút értéke I min /1000 alatt maradt. A jobb oldalon a hengeres sejtmodell sematikus rajza látható: a sejt dendritje mm mélyen fekszik, a sejttest 1.46 mm mélységben, míg az axon 1.47-től 1.87 mm-ig tart. B: A tüzelés által létrehozott elektromos potenciál a sejttől 25 µm távolságban a sejttesthez közel. C: A monopólus (szaggatott vonal) és az ellenáram modell illeszkedési hibájának időfüggése, logaritmikus tengelyen. Az árambefecskendezés az időtengely 0 értékénél kezdődött. A függőleges pontozott vonalak az A ábrán azt az időtartományt jelölik, amikor csak az axon kezdeti szakasza aktív. Ez egybe esett az akciós potenciál negatív hullámának kezdetétől a csúcsági tartó időszakkal a B ábrán. Ebben az intervallumban az ellenáram modell igen alacsony illesztési hibát ad a C ábrán. 30
Adatelemzési eljárások az idegrendszer kutatásban Somogyvári Zoltán
 Adatelemzési eljárások az idegrendszer kutatásban Somogyvári Zoltán MTA KFKI Részecske és Magfizikai Intézet, Biofizikai osztály Az egy adatsorra (idősorra) is alkalmazható módszerek Példa: Az epileptikus
Adatelemzési eljárások az idegrendszer kutatásban Somogyvári Zoltán MTA KFKI Részecske és Magfizikai Intézet, Biofizikai osztály Az egy adatsorra (idősorra) is alkalmazható módszerek Példa: Az epileptikus
Az agykéreg dinamikájának modell alapú vizsgálata: az egyedi idegsejtektől a hálózatokig. Somogyvári Zoltán
 Az agykéreg dinamikájának modell alapú vizsgálata: az egyedi idegsejtektől a hálózatokig Doktori értekezés Somogyvári Zoltán Semmelweis Egyetem Szentágothai János Idegtudományi Doktori Iskola Témavezető:
Az agykéreg dinamikájának modell alapú vizsgálata: az egyedi idegsejtektől a hálózatokig Doktori értekezés Somogyvári Zoltán Semmelweis Egyetem Szentágothai János Idegtudományi Doktori Iskola Témavezető:
Az agykéreg dinamikájának modell alapú vizsgálata: az egyedi idegsejtektől a hálózatokig
 Az agykéreg dinamikájának modell alapú vizsgálata: az egyedi idegsejtektől a hálózatokig Doktori tézisek Somogyvári Zoltán Semmelweis Egyetem Szentágothai János Idegtudományi Doktori Iskola Témavezető:
Az agykéreg dinamikájának modell alapú vizsgálata: az egyedi idegsejtektől a hálózatokig Doktori tézisek Somogyvári Zoltán Semmelweis Egyetem Szentágothai János Idegtudományi Doktori Iskola Témavezető:
Az egyedi neuronoktól az EEG hullámokig Somogyvári Zoltán
 Az egyedi neuronoktól az EEG hullámokig Somogyvári Zoltán MTA KFKI Részecske és Magfizikai Intézet, Biofizikai osztály Az állati elektromosság felfedezése 1792 Galvani, De Viribus - Electricitatis in Motu
Az egyedi neuronoktól az EEG hullámokig Somogyvári Zoltán MTA KFKI Részecske és Magfizikai Intézet, Biofizikai osztály Az állati elektromosság felfedezése 1792 Galvani, De Viribus - Electricitatis in Motu
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Mikroelektródás képalkotó eljárások Somogyvári Zoltán
 Somogyvári Zoltán Magyar Tudományos Akadémia Wigner Fizikai Kutatóközpont Részecske és Magfizikai Intézet Elméleti Osztály Elméleti Idegtudomány és Komplex Rendszerek Kutatócsoport Az agy szürkeállománya
Somogyvári Zoltán Magyar Tudományos Akadémia Wigner Fizikai Kutatóközpont Részecske és Magfizikai Intézet Elméleti Osztály Elméleti Idegtudomány és Komplex Rendszerek Kutatócsoport Az agy szürkeállománya
Termodinamikai egyensúlyi potenciál (Nernst, Donnan). Diffúziós potenciál, Goldman-Hodgkin-Katz egyenlet.
 Termodinamikai egyensúlyi potenciál (Nernst, Donnan). Diffúziós potenciál, Goldman-Hodgkin-Katz egyenlet. Biológiai membránok passzív elektromos tulajdonságai. A sejtmembrán kondenzátorként viselkedik
Termodinamikai egyensúlyi potenciál (Nernst, Donnan). Diffúziós potenciál, Goldman-Hodgkin-Katz egyenlet. Biológiai membránok passzív elektromos tulajdonságai. A sejtmembrán kondenzátorként viselkedik
-2σ. 1. A végtelen kiterjedésű +σ és 2σ felületi töltéssűrűségű síklapok terében az ábrának megfelelően egy dipól helyezkedik el.
 1. 2. 3. Mondat E1 E2 Össz Energetikai mérnöki alapszak Mérnöki fizika 2. ZH NÉV:.. 2018. május 15. Neptun kód:... g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus
1. 2. 3. Mondat E1 E2 Össz Energetikai mérnöki alapszak Mérnöki fizika 2. ZH NÉV:.. 2018. május 15. Neptun kód:... g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
2. (b) Hővezetési problémák. Utolsó módosítás: február25. Dr. Márkus Ferenc BME Fizika Tanszék
 2. (b) Hővezetési problémák Utolsó módosítás: 2013. február25. A változók szétválasztásának módszere (5) 1 Az Y(t)-re vonakozó megoldás: Így: A probléma megoldása n-re összegzés után: A peremfeltételeknek
2. (b) Hővezetési problémák Utolsó módosítás: 2013. február25. A változók szétválasztásának módszere (5) 1 Az Y(t)-re vonakozó megoldás: Így: A probléma megoldása n-re összegzés után: A peremfeltételeknek
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Egy idegsejt működése. a. Nyugalmi potenciál b. Transzport proteinek c. Akciós potenciál
 Egy idegsejt működése a. Nyugalmi potenciál b. Transzport proteinek c. Akciós potenciál Nyugalmi potenciál Az ionok vándorlása 5. Alacsonyabb koncentráció ioncsatorna membrán Passzív Aktív 3 tényező határozza
Egy idegsejt működése a. Nyugalmi potenciál b. Transzport proteinek c. Akciós potenciál Nyugalmi potenciál Az ionok vándorlása 5. Alacsonyabb koncentráció ioncsatorna membrán Passzív Aktív 3 tényező határozza
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Nagy számok törvényei Statisztikai mintavétel Várható érték becslése. Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem
 agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
STATISZTIKAI PROBLÉMÁK A
 STATISZTIKAI PROBLÉMÁK A HULLÁMTÉR REPRODUKCIÓ TERÜLETÉN 2012. május 3., Budapest Firtha Gergely PhD hallgató, Akusztikai Laboratórium BME Híradástechnikai Tanszék firtha@hit.bme.hu Tartalom A hangtér
STATISZTIKAI PROBLÉMÁK A HULLÁMTÉR REPRODUKCIÓ TERÜLETÉN 2012. május 3., Budapest Firtha Gergely PhD hallgató, Akusztikai Laboratórium BME Híradástechnikai Tanszék firtha@hit.bme.hu Tartalom A hangtér
a. Nyugalmi potenciál b. Transzport proteinek c. Akciós potenciál. Nyugalmi potenciál. 3 tényező határozza meg:
 Egy idegsejt működése a. Nyugalmi potenciál b. Transzport proteinek c. Nyugalmi potenciál Az ionok vándorlása 5. Alacsonyabb koncentráció ioncsatorna membrán Passzív Aktív 3 tényező határozza meg: 1. Koncentráció
Egy idegsejt működése a. Nyugalmi potenciál b. Transzport proteinek c. Nyugalmi potenciál Az ionok vándorlása 5. Alacsonyabb koncentráció ioncsatorna membrán Passzív Aktív 3 tényező határozza meg: 1. Koncentráció
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Elektromágneses hullámok
 Bevezetés a modern fizika fejezeteibe 2. (a) Elektromágneses hullámok Utolsó módosítás: 2015. október 3. 1 A Maxwell-egyenletek (1) (2) (3) (4) E: elektromos térerősség D: elektromos eltolás H: mágneses
Bevezetés a modern fizika fejezeteibe 2. (a) Elektromágneses hullámok Utolsó módosítás: 2015. október 3. 1 A Maxwell-egyenletek (1) (2) (3) (4) E: elektromos térerősség D: elektromos eltolás H: mágneses
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9
 A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
Az Ampère-Maxwell-féle gerjesztési törvény
 Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
b) Ábrázolja ugyanabban a koordinátarendszerben a g függvényt! (2 pont) c) Oldja meg az ( x ) 2
 1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
Transzportfolyamatok a biológiai rendszerekben
 A nyugalmi potenciál jelentősége Transzportfolyamatok a biológiai rendszerekben Transzportfolyamatok a sejt nyugalmi állapotában a sejt homeosztázisának (sejttérfogat, ph) fenntartása ingerlékenység érzékelés
A nyugalmi potenciál jelentősége Transzportfolyamatok a biológiai rendszerekben Transzportfolyamatok a sejt nyugalmi állapotában a sejt homeosztázisának (sejttérfogat, ph) fenntartása ingerlékenység érzékelés
Vezetők elektrosztatikus térben
 Vezetők elektrosztatikus térben Vezető: a töltések szabadon elmozdulhatnak Ha a vezető belsejében a térerősség nem lenne nulla akkor áram folyna. Ha a felületen a térerősségnek lenne tangenciális (párhuzamos)
Vezetők elektrosztatikus térben Vezető: a töltések szabadon elmozdulhatnak Ha a vezető belsejében a térerősség nem lenne nulla akkor áram folyna. Ha a felületen a térerősségnek lenne tangenciális (párhuzamos)
Funkcionális konnektivitás vizsgálata fmri adatok alapján
 Funkcionális konnektivitás vizsgálata fmri adatok alapján Képalkotási technikák 4 Log Resolution (mm) 3 Brain EEG & MEG fmri TMS PET Lesions 2 Column 1 0 Lamina -1 Neuron -2 Dendrite -3 Synapse -4 Mikrolesions
Funkcionális konnektivitás vizsgálata fmri adatok alapján Képalkotási technikák 4 Log Resolution (mm) 3 Brain EEG & MEG fmri TMS PET Lesions 2 Column 1 0 Lamina -1 Neuron -2 Dendrite -3 Synapse -4 Mikrolesions
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 5. mérés: Elektronspin rezonancia. 2008. március 18.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Membránpotenciál, akciós potenciál
 A nyugalmi membránpotenciál Membránpotenciál, akciós potenciál Fizika-Biofizika 2015.november 3. Nyugalomban valamennyi sejt belseje negatív a külső felszínhez képest: negatív nyugalmi potenciál (Em: -30
A nyugalmi membránpotenciál Membránpotenciál, akciós potenciál Fizika-Biofizika 2015.november 3. Nyugalomban valamennyi sejt belseje negatív a külső felszínhez képest: negatív nyugalmi potenciál (Em: -30
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Q 1 D Q 2 (D x) 2 (1.1)
 . Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
. Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Tanulás az idegrendszerben. Structure Dynamics Implementation Algorithm Computation - Function
 Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Orvosi jelfeldolgozás. Információ. Információtartalom. Jelek osztályozása De, mi az a jel?
 Orvosi jelfeldolgozás Információ De, mi az a jel? Jel: Információt szolgáltat (információ: új ismeretanyag, amely csökkenti a bizonytalanságot).. Megjelent.. Panasza? információ:. Egy beteg.. Fáj a fogam.
Orvosi jelfeldolgozás Információ De, mi az a jel? Jel: Információt szolgáltat (információ: új ismeretanyag, amely csökkenti a bizonytalanságot).. Megjelent.. Panasza? információ:. Egy beteg.. Fáj a fogam.
Modern Fizika Labor. 5. ESR (Elektronspin rezonancia) Fizika BSc. A mérés dátuma: okt. 25. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
MATEMATIKA HETI 5 ÓRA. IDŐPONT: 2010. Június 4.
 EURÓPAI ÉRETTSÉGI 2010 MATEMATIKA HETI 5 ÓRA IDŐPONT: 2010. Június 4. A VIZSGA IDŐTARTAMA: 4 óra (240 perc) ENGEDÉLYEZETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 2010 MATEMATIKA HETI 5 ÓRA IDŐPONT: 2010. Június 4. A VIZSGA IDŐTARTAMA: 4 óra (240 perc) ENGEDÉLYEZETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI
 SZENT ISTVÁN EGYETEM GÖDÖLLŐ MECHANIKAI ÉS GÉPTANI INTÉZET A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI Dr. M. Csizmadia Béla egyetemi tanár, az MMK Gépészeti Tagozatának elnöke Budapest 2013. október. 25. BPMK
SZENT ISTVÁN EGYETEM GÖDÖLLŐ MECHANIKAI ÉS GÉPTANI INTÉZET A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI Dr. M. Csizmadia Béla egyetemi tanár, az MMK Gépészeti Tagozatának elnöke Budapest 2013. október. 25. BPMK
x 2 e x dx c) (3x 2 2x)e 2x dx x sin x dx f) x cosxdx (1 x 2 )(sin 2x 2 cos 3x) dx e 2x cos x dx k) e x sin x cosxdx x ln x dx n) (2x + 1) ln 2 x dx
 Integrálszámítás II. Parciális integrálás. g) i) l) o) e ( + )(e e ) cos h) e sin j) (sin 3 cos) m) arctg p) arcsin e (3 )e sin f) cos ( )(sin cos 3) e cos k) e sin cos ln n) ( + ) ln. e 3 e cos 3 3 cos
Integrálszámítás II. Parciális integrálás. g) i) l) o) e ( + )(e e ) cos h) e sin j) (sin 3 cos) m) arctg p) arcsin e (3 )e sin f) cos ( )(sin cos 3) e cos k) e sin cos ln n) ( + ) ln. e 3 e cos 3 3 cos
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Méréselmélet MI BSc 1
 Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
1. ábra. 24B-19 feladat
 . gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
. gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
STATISZTIKA. A maradék független a kezelés és blokk hatástól. Maradékok leíró statisztikája. 4. A modell érvényességének ellenőrzése
 4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
Molekuláris dinamika I. 10. előadás
 Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Wavelet transzformáció
 1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld ábra ábra
 . Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
. Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni.
 Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni. Kezdjük a sort a menetidőgörbékről, illetve az NMO korrekcióról tanultakkal. A következő ábrán
Eddigi tanulmányaink alapján már egy sor, a szeizmikában általánosan használt műveletet el tudunk végezni. Kezdjük a sort a menetidőgörbékről, illetve az NMO korrekcióról tanultakkal. A következő ábrán
Digitális mérőműszerek. Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt.
 Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt. MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális jel esetében?
Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt. MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális jel esetében?
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Gépészeti rendszertechnika (NGB_KV002_1)
 Gépészeti rendszertechnika (NGB_KV002_1) 2. Óra Kőrös Péter Közúti és Vasúti Járművek Tanszék Tanszéki mérnök (IS201 vagy a tanszéken) E-mail: korosp@ga.sze.hu Web: http://www.sze.hu/~korosp http://www.sze.hu/~korosp/gepeszeti_rendszertechnika/
Gépészeti rendszertechnika (NGB_KV002_1) 2. Óra Kőrös Péter Közúti és Vasúti Járművek Tanszék Tanszéki mérnök (IS201 vagy a tanszéken) E-mail: korosp@ga.sze.hu Web: http://www.sze.hu/~korosp http://www.sze.hu/~korosp/gepeszeti_rendszertechnika/
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017.
 Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/91/106534674.jpg) [Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
[Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
cos 2 (2x) 1 dx c) sin(2x)dx c) cos(3x)dx π 4 cos(2x) dx c) 5sin 2 (x)cos(x)dx x3 5 x 4 +11dx arctg 11 (2x) 4x 2 +1 π 4
 Integrálszámítás I. Végezze el a következő integrálásokat:. α, haα sin() cos() e f) a sin h) () cos ().. 5 4 ( ) e + 4 sin h) (+) sin() sin() cos() + f) 5 i) cos ( +) 7 4. 4 (+) 6 4 cos() 5 +7 5. ( ) sin()cos
Integrálszámítás I. Végezze el a következő integrálásokat:. α, haα sin() cos() e f) a sin h) () cos ().. 5 4 ( ) e + 4 sin h) (+) sin() sin() cos() + f) 5 i) cos ( +) 7 4. 4 (+) 6 4 cos() 5 +7 5. ( ) sin()cos
Végeselem modellezés alapjai 1. óra
 Végeselem modellezés alapjai. óra Gyenge alak, Tesztfüggvény, Lagrange-féle alakfüggvény, Stiness mátrix Kivonat Az óra célja, hogy megismertesse a végeselem módszer (FEM) alkalmazását egy egyszer probléma,
Végeselem modellezés alapjai. óra Gyenge alak, Tesztfüggvény, Lagrange-féle alakfüggvény, Stiness mátrix Kivonat Az óra célja, hogy megismertesse a végeselem módszer (FEM) alkalmazását egy egyszer probléma,
0,424 0,576. f) P (X 2 = 3) g) P (X 3 = 1) h) P (X 4 = 1 vagy 2 X 2 = 2) i) P (X 7 = 3, X 4 = 1, X 2 = 2 X 0 = 2) j) P (X 7 = 3, X 4 = 1, X 2 = 2)
 Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Pelletek térfogatának meghatározása Bayes-i analízissel
 Pelletek térfogatának meghatározása Bayes-i analízissel Szepesi Tamás KFKI-RMKI, Budapest, Hungary P. Cierpka, Kálvin S., Kocsis G., P.T. Lang, C. Wittmann 2007. február 27. Tartalom 1. Motiváció ELM-keltés
Pelletek térfogatának meghatározása Bayes-i analízissel Szepesi Tamás KFKI-RMKI, Budapest, Hungary P. Cierpka, Kálvin S., Kocsis G., P.T. Lang, C. Wittmann 2007. február 27. Tartalom 1. Motiváció ELM-keltés
LOKÁLIS IONOSZFÉRA MODELLEZÉS ÉS ALKALMAZÁSA A GNSS HELYMEGHATÁROZÁSBAN
 LOKÁLIS IONOSZFÉRA MODELLEZÉS ÉS ALKALMAZÁSA A GNSS HELYMEGHATÁROZÁSBAN Juni Ildikó Budapesti Műszaki és Gazdaságtudományi Egyetem BSc IV. évfolyam Konzulens: Dr. Rózsa Szabolcs MFTT 29. Vándorgyűlés,
LOKÁLIS IONOSZFÉRA MODELLEZÉS ÉS ALKALMAZÁSA A GNSS HELYMEGHATÁROZÁSBAN Juni Ildikó Budapesti Műszaki és Gazdaságtudományi Egyetem BSc IV. évfolyam Konzulens: Dr. Rózsa Szabolcs MFTT 29. Vándorgyűlés,
KUTATÁSI JELENTÉS. Multilaterációs radarrendszer kutatása. Szüllő Ádám
 KUTATÁSI JELENTÉS Multilaterációs radarrendszer kutatása Szüllő Ádám 212 Bevezetés A Mikrohullámú Távérzékelés Laboratórium jelenlegi K+F tevékenységei közül ezen jelentés a multilaterációs radarrendszerek
KUTATÁSI JELENTÉS Multilaterációs radarrendszer kutatása Szüllő Ádám 212 Bevezetés A Mikrohullámú Távérzékelés Laboratórium jelenlegi K+F tevékenységei közül ezen jelentés a multilaterációs radarrendszerek
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
A maximum likelihood becslésről
 A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
Biometria az orvosi gyakorlatban. Korrelációszámítás, regresszió
 SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
Kirchhoff 2. törvénye (huroktörvény) szerint az áramkörben levő elektromotoros erők. E i = U j (3.1)
 3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
Matematika 11 Koordináta geometria. matematika és fizika szakos középiskolai tanár. > o < szeptember 27.
 Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
ÁRAMKÖRÖK SZIMULÁCIÓJA
 ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
Least Squares becslés
 Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Alkalmazás a makrókanónikus sokaságra: A fotongáz
 Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
6. Függvények. 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban?
 6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
Az agyi jelek adaptív feldolgozása MENTÁ LIS FÁ R A DT S ÁG MÉRÉSE
 Az agyi jelek adaptív feldolgozása MENTÁ LIS FÁ R A DT S ÁG MÉRÉSE Bevezetés I. A fáradtság lehet fizikai: a normál testi funkciók hiánya mentális: csökkent agyi aktivitás vagy kognitív funkciók. Megjelenhet
Az agyi jelek adaptív feldolgozása MENTÁ LIS FÁ R A DT S ÁG MÉRÉSE Bevezetés I. A fáradtság lehet fizikai: a normál testi funkciók hiánya mentális: csökkent agyi aktivitás vagy kognitív funkciók. Megjelenhet
Függvény határérték összefoglalás
 Függvény határérték összefoglalás Függvény határértéke: Def: Függvény: egyértékű reláció. (Vagyis minden értelmezési tartománybeli elemhez, egyértelműen rendelünk hozzá egy elemet az értékkészletből. Vagyis
Függvény határérték összefoglalás Függvény határértéke: Def: Függvény: egyértékű reláció. (Vagyis minden értelmezési tartománybeli elemhez, egyértelműen rendelünk hozzá egy elemet az értékkészletből. Vagyis
Koordináta geometria III.
 Koordináta geometria III. TÉTEL: A P (x; y) pont akkor és csak akkor illeszkedik a K (u; v) középpontú r sugarú körre (körvonalra), ha (x u) 2 + (y v) 2 = r 2. Ez az összefüggés a K (u; v) középpontú r
Koordináta geometria III. TÉTEL: A P (x; y) pont akkor és csak akkor illeszkedik a K (u; v) középpontú r sugarú körre (körvonalra), ha (x u) 2 + (y v) 2 = r 2. Ez az összefüggés a K (u; v) középpontú r
Optimalizálás alapfeladata Legmeredekebb lejtő Lagrange függvény Log-barrier módszer Büntetőfüggvény módszer 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
Debreceni Egyetem Orvos- és Egészségtudományi Centrum Biofizikai és Sejtbiológiai Intézet
 Debreceni Egyetem Orvos- és Egészségtudományi Centrum Biofizikai és Sejtbiológiai Intézet Az ioncsatorna fehérjék szerkezete, működése és szabályozása Panyi György www.biophys.dote.hu Mesterséges membránok
Debreceni Egyetem Orvos- és Egészségtudományi Centrum Biofizikai és Sejtbiológiai Intézet Az ioncsatorna fehérjék szerkezete, működése és szabályozása Panyi György www.biophys.dote.hu Mesterséges membránok
Transzformátor rezgés mérés. A BME Villamos Energetika Tanszéken
 Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Normák, kondíciószám
 Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Digitális mérőműszerek
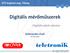 KTE Szakmai nap, Tihany Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt KT-Electronic MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális TV jel esetében? Milyen paraméterekkel
KTE Szakmai nap, Tihany Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt KT-Electronic MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális TV jel esetében? Milyen paraméterekkel
Gauss-Jordan módszer Legkisebb négyzetek módszere, egyenes LNM, polinom LNM, függvény. Lineáris algebra numerikus módszerei
 A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
17. Diffúzió vizsgálata
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.11.24. A beadás dátuma: 2011.12.04. A mérés száma és címe: 17. Diffúzió vizsgálata A mérést végezte: Németh Gergely Értékelés: Elméleti háttér Mi is
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.11.24. A beadás dátuma: 2011.12.04. A mérés száma és címe: 17. Diffúzió vizsgálata A mérést végezte: Németh Gergely Értékelés: Elméleti háttér Mi is
Fizika 1 Elektrodinamika beugró/kis kérdések
 Fizika 1 Elektrodinamika beugró/kis kérdések 1.) Írja fel a 4 Maxwell-egyenletet lokális (differenciális) alakban! rot = j+ D rot = B div B=0 div D=ρ : elektromos térerősség : mágneses térerősség D : elektromos
Fizika 1 Elektrodinamika beugró/kis kérdések 1.) Írja fel a 4 Maxwell-egyenletet lokális (differenciális) alakban! rot = j+ D rot = B div B=0 div D=ρ : elektromos térerősség : mágneses térerősség D : elektromos
Statisztika I. 8. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
A mérés problémája a pedagógiában. Dr. Nyéki Lajos 2015
 A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
Ipari robotok megfogó szerkezetei
 IPARI ROBOTOK Ipari robotok megfogó szerkezetei 6. előadás Dr. Pintér József Tananyag vázlata Ipari robotok megfogó szerkezetei 1. Effektor fogalma 2. Megfogó szerkezetek csoportosítása 3. Mechanikus megfogó
IPARI ROBOTOK Ipari robotok megfogó szerkezetei 6. előadás Dr. Pintér József Tananyag vázlata Ipari robotok megfogó szerkezetei 1. Effektor fogalma 2. Megfogó szerkezetek csoportosítása 3. Mechanikus megfogó
Mágneses mező jellemzése
 pólusok dipólus mező mező jellemzése vonalak pólusok dipólus mező kölcsönhatás A mágnesek egymásra és a vastárgyakra erőhatást fejtenek ki. vonalak vonzó és taszító erő pólusok dipólus mező pólusok északi
pólusok dipólus mező mező jellemzése vonalak pólusok dipólus mező kölcsönhatás A mágnesek egymásra és a vastárgyakra erőhatást fejtenek ki. vonalak vonzó és taszító erő pólusok dipólus mező pólusok északi
