Intelligens Rendszerek Elmélete. Párhuzamos keresés genetikus algoritmusokkal
|
|
|
- Balázs Bogdán
- 7 évvel ezelőtt
- Látták:
Átírás
1 Intelligens Rendszerek Elmélete Dr. Kutor László Párhuzamos keresés genetikus algoritmusokkal login: ire jelszó: IRE0 IRE / A természet általános kereső algoritmusa: a genetikus algoritmus IRE /
2 Az élet információ tárolói IRE / Orvosi Nobel díj 009. (okt. ) Elisabeth Blackburn Carol Greider, Jack W. Szostak (ausztráliai-amerikai) (amerikai) (angol-amerikai) A telomerek és a telomeráz enzim felfedezéséért IRE /
3 Természetes és mesterséges genetikus terminológia Természetes Mesterséges Kromoszóma Karakterfüzér (sztring) (a sejtek örökletes tulajdonságokat hordozó anyaga) Gén Jellemző, karakter (az öröklődő tulajdonságokkat hordozó kromoszóma egy része, (nukleinsav molekula)) Allél A karakter (jellemző) értéke Lókusz Karakter pozíció Genotípus Karakterfüzér szerkezet (az örökletes tulajdonságok összessége) Fenotípus Paraméter készlet (az élőlény alaktani és élettani sajátosságainak összessége. Az örökletes és a környezet együttes hatására létrejött megjelenési alak) IRE / A genetikus algoritmus (GA) alkalmazási vázlata. Az optimalizálandó rendszer leírása (mesterséges kromoszómába) A rendszerre jellemző változók. Kezdeti generáció egymást követő generációk. GA GA GA GA GA sorozatos alkalmazása IRE /
4 A genetikus algoritmus alkalmazásának feltételei. Egyértelmű rendszerleírás egy rendszerváltozókat tartalmazó karakterfüzérbe az un. mesterséges kromoszómába.. Reprezentatív populáció, ami azonos formában különböző jellemzőkkel bíró egyedek (rendszerek) leírását tartalmazza.. Alkalmas mérési módszer, mellyel a vizsgált rendszerek jóságát meg lehet határozni. IRE / A genetikus algoritmusok operátorai Alap operátorok: Szelekció Kereszteződés Mutáció Alacsony szintű operátorok: Dominancia Inverzió Törlődés Halkítás (erősítés) Andrew Z. Fire Craig C. Mello Orvosi Nobel díj Mario Capecchi Oliver Smithies Martin Evans Kikapcsolás knock out Populációra vonatkozó operátorok: Migráció Házassági korlátozás Jóság transzformáló függvények IRE /
5 Kiválasztási mechanizmusok A relatív jósággal (fitness) arányos un. rulettkerék algoritmus Csak a legjobbakat kiválasztó algoritmus elicista S = n F i i= Paraméterek: populáció méret, Reprodukciós arány (állandó, csökkenő, bővülő,..) IRE /9 A genetikus algoritmus alkalmazásának menete. A mesterséges kromoszóma (leíró adatfüzér) szerkezetének kidolgozása (változók és jellemzői). Kezdeti populáció létrehozása. A populációt alkotó egyedek értékelése, az abszolút- majd a relatív jóság meghatározása. A genetikus operátorok alkalmazásával új populáció létrehozása (pl.:szelekció, keresztezés, mutáció, stb ). A.-ik és a.-ik lépés ismétlése, amíg a megállási feltétel nem teljesül. IRE /0
6 A relatív jósággal (fitness) arányos un. rulettkerék algoritmus. Az egyedek jóságának meghatározása: Fi=f(Ii). A populáció összes tagja jóságának meghatározása: n. Az egyedek relatív jóságának kiszámítása: S = F i i= (Teljes Relatív Fitness TRF=):. és 00 közötti szám hozzárendelése a populáció minden tagjához a relatív jóságuknak megfelelően. (n = a jelenlegi populáció mérete). Egy m véletlen szám generálása és 00 között (m: az új populáció mérete). m egyed (génstruktúrájának) másolása az új generációba, IRE / Kereszteződés Paraméterek: kereszteződési pontok száma kereszteződési pontok helye kiinduló sztringek: új sztringek: IRE /
7 Mutáció Paraméterek: mutációs helyek száma mutációs változás tartománya kiinduló sztring: új sztring: M M M M IRE / A genetikus algoritmus előnyei a hagyományos kereső algoritmusokhoz képest A keresési tér több pontját vizsgálja egyszerre (párhuzamosság) Csak jellemzőket tartalmazó sztringgel dolgozik, a változók értelmezésétől függetlenül, ezért általános keresési algoritmus A véletlenszerű változók használata miatt a lokális minimumokra kevésbé érzékeny. Mivel a keresési szabályok nem determinisztikusak, hanem valószínűségi szabályokat alkalmaznak, így az NP teljes jellegű problémákra is megközelítést adhat. IRE /
8 A genetikus algoritmusok korlátai Túlságosan nagy jóságú egyedek eluralhatják a populációt Ha csak minimális különbségek vannak az egyedek között akkor nincs javulás Részleges megoldások: Különböző jóság transzformáló eljárások a keresés előrehaladtával (pl. nagy különbségek kiegyenlítése a keresés elején, kis különbségek felnagyítása a keresés vége felé) f g (x i ) = α g + β g f(x i ) IRE / Példa a GA alkalmazására f(x) = x + x +.x +x +.x e Σ x i x i értelmezési tartománya -0-től +0-ig Kezdeti populáció száma: 0 Megállási feltétel: f(x) >=., vagy 0 generáció Eredmények: x, x, x, x, x elért generációk száma Példa megoldás: x = =0, x = =0, x = =0, x = =-, x = =0, g= 9 IRE / i=
9 Kérdések Milyen tényezők befolyásolják a genetikus algoritmusok sikeres alkalmazását? Milyen problémák megoldásában segíthet a genetikus algoritmusok alkalmazása?. Lehet-e gyors eredményt elérni genetikus algoritmusokkal? IRE /
Intelligens Rendszerek Elmélete. Párhuzamos keresés genetikus algoritmusokkal. A genetikus algoritmus működése. Az élet információ tárolói
 Intelligens Rendszerek Elmélete dr. Kutor László Párhuzamos keresés genetikus algoritmusokkal http://mobil.nik.bmf.hu/tantargyak/ire.html login: ire jelszó: IRE07 IRE 5/ Természetes és mesterséges genetikus
Intelligens Rendszerek Elmélete dr. Kutor László Párhuzamos keresés genetikus algoritmusokkal http://mobil.nik.bmf.hu/tantargyak/ire.html login: ire jelszó: IRE07 IRE 5/ Természetes és mesterséges genetikus
Algoritmusok Tervezése. 9. Előadás Genetikus Algoritmusok Dr. Bécsi Tamás
 Algoritmusok Tervezése 9. Előadás Genetikus Algoritmusok Dr. Bécsi Tamás Biológiai háttér (nagyvonalúan) A sejt genetikai információit hordozó DNS általában kromoszómának nevezett makromolekulákba van
Algoritmusok Tervezése 9. Előadás Genetikus Algoritmusok Dr. Bécsi Tamás Biológiai háttér (nagyvonalúan) A sejt genetikai információit hordozó DNS általában kromoszómának nevezett makromolekulákba van
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Dr. habil. Maróti György
 infokommunikációs technológiák III.8. MÓDSZER KIDOLGOZÁSA ALGORITMUSOK ÁTÜLTETÉSÉRE KIS SZÁMÍTÁSI TELJESÍTMÉNYŰ ESZKÖZÖKBŐL ÁLLÓ NÉPES HETEROGÉN INFRASTRUKTÚRA Dr. habil. Maróti György maroti@dcs.uni-pannon.hu
infokommunikációs technológiák III.8. MÓDSZER KIDOLGOZÁSA ALGORITMUSOK ÁTÜLTETÉSÉRE KIS SZÁMÍTÁSI TELJESÍTMÉNYŰ ESZKÖZÖKBŐL ÁLLÓ NÉPES HETEROGÉN INFRASTRUKTÚRA Dr. habil. Maróti György maroti@dcs.uni-pannon.hu
Genetikus algoritmusok
 Genetikus algoritmusok Zsolnai Károly - BME CS zsolnai@cs.bme.hu Keresőalgoritmusok osztályai Véletlent használó algoritmusok Keresőalgoritmusok Kimerítő algoritmusok Dinamikus programozás BFS DFS Tabu
Genetikus algoritmusok Zsolnai Károly - BME CS zsolnai@cs.bme.hu Keresőalgoritmusok osztályai Véletlent használó algoritmusok Keresőalgoritmusok Kimerítő algoritmusok Dinamikus programozás BFS DFS Tabu
A genetikus algoritmus, mint a részletes modell többszempontú és többérdekű "optimálásának" általános és robosztus módszere
 A genetikus algoritmus, mint a részletes modell többszempontú és többérdekű "optimálásának" általános és robosztus módszere Kaposvári Egyetem, Informatika Tanszék I. Kaposvári Gazdaságtudományi Konferencia
A genetikus algoritmus, mint a részletes modell többszempontú és többérdekű "optimálásának" általános és robosztus módszere Kaposvári Egyetem, Informatika Tanszék I. Kaposvári Gazdaságtudományi Konferencia
értékel függvény: rátermettségi függvény (tness function)
 Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Intelligens Rendszerek Elmélete. Versengéses és önszervező tanulás neurális hálózatokban
 Intelligens Rendszerek Elmélete : dr. Kutor László Versengéses és önszervező tanulás neurális hálózatokban http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 9/1 Processzor Versengéses
Intelligens Rendszerek Elmélete : dr. Kutor László Versengéses és önszervező tanulás neurális hálózatokban http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 9/1 Processzor Versengéses
Az Informatika Elméleti Alapjai
 Az Informatika Elméleti Alapjai dr. Kutor László Az üzenet információ-tartalma és redundanciája Tömörítő algoritmusok elemzése http://mobil.nik.bmf.hu/tantárgyak/iea.html Felhasználónév: iea Jelszó: IEA07
Az Informatika Elméleti Alapjai dr. Kutor László Az üzenet információ-tartalma és redundanciája Tömörítő algoritmusok elemzése http://mobil.nik.bmf.hu/tantárgyak/iea.html Felhasználónév: iea Jelszó: IEA07
Megkülönböztetett kiszolgáló routerek az
 Megkülönböztetett kiszolgáló routerek az Interneten Megkülönböztetett kiszolgálás A kiszolgáló architektúrák minősége az Interneten: Integrált kiszolgálás (IntServ) Megkülönböztetett kiszolgálás (DiffServ)
Megkülönböztetett kiszolgáló routerek az Interneten Megkülönböztetett kiszolgálás A kiszolgáló architektúrák minősége az Interneten: Integrált kiszolgálás (IntServ) Megkülönböztetett kiszolgálás (DiffServ)
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel - csak lokális információra alapozva Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Lokálisan
Mesterséges Intelligencia MI Problémamegoldás kereséssel - csak lokális információra alapozva Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Lokálisan
Genetikus algoritmusok az L- rendszereken alapuló. Werner Ágnes
 Genetikus algoritmusok az L- rendszereken alapuló növénymodellezésben Werner Ágnes Motiváció: Procedurális modellek a növénymodellezésben: sok tervezési munka a felhasználónak ismerni kell az eljárás részleteit
Genetikus algoritmusok az L- rendszereken alapuló növénymodellezésben Werner Ágnes Motiváció: Procedurális modellek a növénymodellezésben: sok tervezési munka a felhasználónak ismerni kell az eljárás részleteit
GROVER-algoritmus. Sinkovicz Péter. ELTE, MSc II dec.15.
 ELTE, MSc II. 2011.dec.15. Áttekintés Feladat Algoritmus Kvantum keresési algoritmus áttekintése Input: N = 2 n elemű tömb, Ψ 1 = 0 1 kezdőállapot, f x0 (x) orákulum függvény. Output: x 0 keresett elem
ELTE, MSc II. 2011.dec.15. Áttekintés Feladat Algoritmus Kvantum keresési algoritmus áttekintése Input: N = 2 n elemű tömb, Ψ 1 = 0 1 kezdőállapot, f x0 (x) orákulum függvény. Output: x 0 keresett elem
Természetes szelekció és adaptáció
 Természetes szelekció és adaptáció Amiről szó lesz öröklődő és variábilis fenotípus természetes szelekció adaptáció evolúció 2. Természetes szelekció Miért fontos a természetes szelekció (TSZ)? 1. C.R.
Természetes szelekció és adaptáció Amiről szó lesz öröklődő és variábilis fenotípus természetes szelekció adaptáció evolúció 2. Természetes szelekció Miért fontos a természetes szelekció (TSZ)? 1. C.R.
Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak.
 Evolúció Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak. Latin eredetű szó, jelentése: kibontakozás Időben egymást
Evolúció Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak. Latin eredetű szó, jelentése: kibontakozás Időben egymást
Universität M Mis is k k olol cic, F Eg a y kultä etem t, für Wi Gazda rts ságcha tudfts o w máis n s yen i scha Kar, ften,
 8. Előadás Speciális optimalizációs eljárások Genetikus algoritmusok OPTIMALIZÁLÁSI ELJÁRÁSOK Gradiens alapú módszerek Véletlent használó módszerek Kimerítő keresésen alapuló módszerek Direkt módszerek
8. Előadás Speciális optimalizációs eljárások Genetikus algoritmusok OPTIMALIZÁLÁSI ELJÁRÁSOK Gradiens alapú módszerek Véletlent használó módszerek Kimerítő keresésen alapuló módszerek Direkt módszerek
Evolúciós algoritmusok
 Evolúciós algoritmusok Evolúció, mint kereső rendszer A problémára adható néhány lehetséges választ, azaz a problématér több egyedét tároljuk egyszerre. Ez a populáció. Kezdetben egy többnyire véletlen
Evolúciós algoritmusok Evolúció, mint kereső rendszer A problémára adható néhány lehetséges választ, azaz a problématér több egyedét tároljuk egyszerre. Ez a populáció. Kezdetben egy többnyire véletlen
Szelekció. Szelekció. A szelekció típusai. Az allélgyakoriságok változása 3/4/2013
 Szelekció Ok: több egyed születik, mint amennyi túlél és szaporodni képes a sikeresség mérése: fitnesz Szelekció Ok: több egyed születik, mint amennyi túlél és szaporodni képes a sikeresség mérése: fitnesz
Szelekció Ok: több egyed születik, mint amennyi túlél és szaporodni képes a sikeresség mérése: fitnesz Szelekció Ok: több egyed születik, mint amennyi túlél és szaporodni képes a sikeresség mérése: fitnesz
Simon Károly Babes Bolyai Tudományegyetem ksimon@cs.ubbcluj.com
 Evolúciósalgoritmusokalkalmazása azadatelemzésben SimonKároly Babes BolyaiTudományegyetem ksimon@cs.ubbcluj.com 1 Evolúciósszámítástechnikaimodellek Evolúciósszámítástechnika:biológiaiinspirációjúkeresésiés
Evolúciósalgoritmusokalkalmazása azadatelemzésben SimonKároly Babes BolyaiTudományegyetem ksimon@cs.ubbcluj.com 1 Evolúciósszámítástechnikaimodellek Evolúciósszámítástechnika:biológiaiinspirációjúkeresésiés
Informatikai Rendszerek Alapjai
 Informatikai Rendszerek Alapjai Dr. Kutor László A redundancia fogalma és mérése Minimális redundanciájú kódok 1. http://uni-obuda.hu/users/kutor/ IRA 2014 könyvtár Óbudai Egyetem, NIK Dr. Kutor László
Informatikai Rendszerek Alapjai Dr. Kutor László A redundancia fogalma és mérése Minimális redundanciájú kódok 1. http://uni-obuda.hu/users/kutor/ IRA 2014 könyvtár Óbudai Egyetem, NIK Dr. Kutor László
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel - lokális információval Pataki Béla Bolgár Bence BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Rugó tervezése
Mesterséges Intelligencia MI Problémamegoldás kereséssel - lokális információval Pataki Béla Bolgár Bence BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Rugó tervezése
biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás
 Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Képrekonstrukció 9. előadás
 Képrekonstrukció 9. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem hv-konvex összefüggő halmazok Mag-burok-szerű rekonstrukció: S. Brunetti, A. Del Lungo, F.
Képrekonstrukció 9. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem hv-konvex összefüggő halmazok Mag-burok-szerű rekonstrukció: S. Brunetti, A. Del Lungo, F.
A Hardy-Weinberg egyensúly. 2. gyakorlat
 A Hardy-Weinberg egyensúly 2. gyakorlat A Hardy-Weinberg egyensúly feltételei: nincs szelekció nincs migráció nagy populációméret (nincs sodródás) nincs mutáció pánmixis van allélgyakoriság azonos hímekben
A Hardy-Weinberg egyensúly 2. gyakorlat A Hardy-Weinberg egyensúly feltételei: nincs szelekció nincs migráció nagy populációméret (nincs sodródás) nincs mutáció pánmixis van allélgyakoriság azonos hímekben
Bevezetés az informatikába
 Bevezetés az informatikába 9. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 9. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Informatikai Rendszerek Tervezése
 Sapientia - Erdélyi Magyar TudományEgyetem (EMTE) Csíkszereda IRT.- 5. kurzus 1 Informatikai Rendszerek Tervezése 4. Előadás: Genetikus algoritmusok Illyés László 1 Tartalom Bevezető A kanonikus genetikus
Sapientia - Erdélyi Magyar TudományEgyetem (EMTE) Csíkszereda IRT.- 5. kurzus 1 Informatikai Rendszerek Tervezése 4. Előadás: Genetikus algoritmusok Illyés László 1 Tartalom Bevezető A kanonikus genetikus
értékel függvény: rátermettségi függvény (tness function)
 Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Populációgenetikai. alapok
 Populációgenetikai alapok Populáció = egyedek egy adott csoportja Az egyedek eltérnek egymástól morfológiailag, de viselkedésüket tekintve is = genetikai különbségek Fenotípus = külső jellegek morfológia,
Populációgenetikai alapok Populáció = egyedek egy adott csoportja Az egyedek eltérnek egymástól morfológiailag, de viselkedésüket tekintve is = genetikai különbségek Fenotípus = külső jellegek morfológia,
HÁLÓZATSZERŰEN MŰKÖDŐ LOGISZTIKÁVAL INTEGRÁLT TERMELÉSÜTEMEZÉS MEGOLDÁSA GENETIKUS ALGORITMUS ALKALMAZÁSÁVAL. OLÁH Béla
 HÁLÓZATSZERŰEN MŰKÖDŐ LOGISZTIKÁVAL INTEGRÁLT TERMELÉSÜTEMEZÉS MEGOLDÁSA GENETIKUS ALGORITMUS ALKALMAZÁSÁVAL OLÁH Béla A TERMELÉSÜTEMEZÉS MEGFOGALMAZÁSA Flow shop: adott n számú termék, melyeken m számú
HÁLÓZATSZERŰEN MŰKÖDŐ LOGISZTIKÁVAL INTEGRÁLT TERMELÉSÜTEMEZÉS MEGOLDÁSA GENETIKUS ALGORITMUS ALKALMAZÁSÁVAL OLÁH Béla A TERMELÉSÜTEMEZÉS MEGFOGALMAZÁSA Flow shop: adott n számú termék, melyeken m számú
Anyai eredet kromoszómák. Zigóta
 2012. február 28. Anyai eredet kromoszómák Apai eredet kromoszómák Zigóta Muslica embrió Fej Nem képz dik fej, az embrió elpusztul A muslica blasztoderma sorstérképe Genetikai boncolás + + STERIL FEJ
2012. február 28. Anyai eredet kromoszómák Apai eredet kromoszómák Zigóta Muslica embrió Fej Nem képz dik fej, az embrió elpusztul A muslica blasztoderma sorstérképe Genetikai boncolás + + STERIL FEJ
Osztott jáva programok automatikus tesztelése. Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január
 Osztott jáva programok automatikus tesztelése Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január Osztott alkalmazások Automatikus tesztelés Tesztelés heurisztikus zaj keltés Tesztelés genetikus
Osztott jáva programok automatikus tesztelése Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január Osztott alkalmazások Automatikus tesztelés Tesztelés heurisztikus zaj keltés Tesztelés genetikus
Gépi tanulás. Neurális hálók, genetikus algoritmus. Közlekedési informatika MSc. Földes Dávid St. 405.
 Gépi tanulás Neurális hálók, genetikus algoritmus Közlekedési informatika MSc Földes Dávid foldes.david@mail.bme.hu St. 405. Tartalom Mesterséges intelligencia - bevezetés Neurális hálózatok Evolúciós
Gépi tanulás Neurális hálók, genetikus algoritmus Közlekedési informatika MSc Földes Dávid foldes.david@mail.bme.hu St. 405. Tartalom Mesterséges intelligencia - bevezetés Neurális hálózatok Evolúciós
Hátterükben egyetlen gén áll, melynek általában számottevő a viselkedésre gyakorolt hatása, öröklési mintázata jellegzetes.
 Múlt órán: Lehetséges tesztfeladatok: Kitől származik a variáció-szelekció paradigma, mely szerint az egyéni, javarészt öröklött különbségek között a társadalmi harc válogat? Fromm-Reichmann Mill Gallton
Múlt órán: Lehetséges tesztfeladatok: Kitől származik a variáció-szelekció paradigma, mely szerint az egyéni, javarészt öröklött különbségek között a társadalmi harc válogat? Fromm-Reichmann Mill Gallton
Az Informatika Elméleti Alapjai
 Az Informatika Elméleti Alapjai dr. Kutor László Minimális redundanciájú kódok Statisztika alapú tömörítő algoritmusok http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 BMF
Az Informatika Elméleti Alapjai dr. Kutor László Minimális redundanciájú kódok Statisztika alapú tömörítő algoritmusok http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 BMF
Tartalomjegyzék. Tartalomjegyzék... 3 Előszó... 9
 ... 3 Előszó... 9 I. Rész: Evolúciós számítások technikái, módszerei...11 1. Bevezetés... 13 1.1 Evolúciós számítások... 13 1.2 Evolúciós algoritmus alapfogalmak... 14 1.3 EC alkalmazásokról általában...
... 3 Előszó... 9 I. Rész: Evolúciós számítások technikái, módszerei...11 1. Bevezetés... 13 1.1 Evolúciós számítások... 13 1.2 Evolúciós algoritmus alapfogalmak... 14 1.3 EC alkalmazásokról általában...
TARTALOMJEGYZÉK. TARTALOMJEGYZÉK...vii ELŐSZÓ... xiii BEVEZETÉS A lágy számításról A könyv célkitűzése és felépítése...
 TARTALOMJEGYZÉK TARTALOMJEGYZÉK...vii ELŐSZÓ... xiii BEVEZETÉS...1 1. A lágy számításról...2 2. A könyv célkitűzése és felépítése...6 AZ ÖSSZETEVŐ LÁGY RENDSZEREK...9 I. BEVEZETÉS...10 3. Az összetevő
TARTALOMJEGYZÉK TARTALOMJEGYZÉK...vii ELŐSZÓ... xiii BEVEZETÉS...1 1. A lágy számításról...2 2. A könyv célkitűzése és felépítése...6 AZ ÖSSZETEVŐ LÁGY RENDSZEREK...9 I. BEVEZETÉS...10 3. Az összetevő
Hidraulikus hálózatok robusztusságának növelése
 Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Termelés- és szolgáltatásmenedzsment
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Előrejelzési módszerek 14. Az előrejelzési modellek felépítése
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Előrejelzési módszerek 14. Az előrejelzési modellek felépítése
Gazdasági matematika II. vizsgadolgozat megoldása, június 10
 Gazdasági matematika II. vizsgadolgozat megoldása, 204. június 0 A dolgozatírásnál íróeszközön kívül más segédeszköz nem használható. A dolgozat időtartama: 90 perc. Ha a dolgozat első részéből szerzett
Gazdasági matematika II. vizsgadolgozat megoldása, 204. június 0 A dolgozatírásnál íróeszközön kívül más segédeszköz nem használható. A dolgozat időtartama: 90 perc. Ha a dolgozat első részéből szerzett
Kockázatalapú változó paraméterű szabályozó kártya kidolgozása a mérési bizonytalanság figyelembevételével
 Kockázatalapú változó paraméterű szabályozó kártya kidolgozása a mérési bizonytalanság figyelembevételével Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és működtetése
Kockázatalapú változó paraméterű szabályozó kártya kidolgozása a mérési bizonytalanság figyelembevételével Hazai hallgatói, illetve kutatói személyi támogatást biztosító rendszer kidolgozása és működtetése
BIOLÓGIA HÁZIVERSENY 1. FORDULÓ BIOKÉMIA, GENETIKA BIOKÉMIA, GENETIKA
 BIOKÉMIA, GENETIKA 1. Nukleinsavak keresztrejtvény (12+1 p) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 1. A nukleinsavak a.-ok összekapcsolódásával kialakuló polimerek. 2. Purinvázas szerves bázis, amely az
BIOKÉMIA, GENETIKA 1. Nukleinsavak keresztrejtvény (12+1 p) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 1. A nukleinsavak a.-ok összekapcsolódásával kialakuló polimerek. 2. Purinvázas szerves bázis, amely az
Evolúció. Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet
 Evolúció Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet Mi az evolúció? Egy folyamat: az élőlények tulajdonságainak változása a környezethez való alkalmazkodásra Egy
Evolúció Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet Mi az evolúció? Egy folyamat: az élőlények tulajdonságainak változása a környezethez való alkalmazkodásra Egy
Zenegenerálás, majdnem természetes zene. Bernád Kinga és Roth Róbert
 Zenegenerálás, majdnem természetes zene Bernád Kinga és Roth Róbert Tartalom 1. Bevezető 2. Eddigi próbálkozások 3. Módszerek 4. Algoritmus bemutatása 5. Összefoglaló (C) Bernád Kinga, Roth Róbert 2 1.
Zenegenerálás, majdnem természetes zene Bernád Kinga és Roth Róbert Tartalom 1. Bevezető 2. Eddigi próbálkozások 3. Módszerek 4. Algoritmus bemutatása 5. Összefoglaló (C) Bernád Kinga, Roth Róbert 2 1.
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
Intelligens Rendszerek Gyakorlata. Neurális hálózatok I.
 : Intelligens Rendszerek Gyakorlata Neurális hálózatok I. dr. Kutor László http://mobil.nik.bmf.hu/tantargyak/ir2.html IRG 3/1 Trend osztályozás Pnndemo.exe IRG 3/2 Hangulat azonosítás Happy.exe IRG 3/3
: Intelligens Rendszerek Gyakorlata Neurális hálózatok I. dr. Kutor László http://mobil.nik.bmf.hu/tantargyak/ir2.html IRG 3/1 Trend osztályozás Pnndemo.exe IRG 3/2 Hangulat azonosítás Happy.exe IRG 3/3
Képrekonstrukció 6. előadás
 Képrekonstrukció 6. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Diszkrét tomográfia (DT) A CT-hez több száz vetület szükséges időigényes költséges károsíthatja
Képrekonstrukció 6. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Diszkrét tomográfia (DT) A CT-hez több száz vetület szükséges időigényes költséges károsíthatja
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134304.jpg) [Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
[Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
Többgénes jellegek. 1. Klasszikus (poligénes) mennyiségi jellegek. 2.Szinte minden jelleg több gén irányítása alatt áll
 Többgénes jellegek Többgénes jellegek 1. 1. Klasszikus (poligénes) mennyiségi jellegek Multifaktoriális jellegek: több gén és a környezet által meghatározott jellegek 2.Szinte minden jelleg több gén irányítása
Többgénes jellegek Többgénes jellegek 1. 1. Klasszikus (poligénes) mennyiségi jellegek Multifaktoriális jellegek: több gén és a környezet által meghatározott jellegek 2.Szinte minden jelleg több gén irányítása
Mesterséges neurális hálózatok II. - A felügyelt tanítás paraméterei, gyorsító megoldásai - Versengéses tanulás
 Mesterséges neurális hálózatok II. - A felügyelt tanítás paraméterei, gyorsító megoldásai - Versengéses tanulás http:/uni-obuda.hu/users/kutor/ IRE 7/50/1 A neurális hálózatok általános jellemzői 1. A
Mesterséges neurális hálózatok II. - A felügyelt tanítás paraméterei, gyorsító megoldásai - Versengéses tanulás http:/uni-obuda.hu/users/kutor/ IRE 7/50/1 A neurális hálózatok általános jellemzői 1. A
Johann Gregor Mendel Az olmüci (Olomouc) és bécsi egyetem diákja Brünni ágostonrendi apát (nem szovjet tudós) Tudatos és nagyon alapos kutat
 10.2.2010 genmisk1 1 Áttekintés Mendel és a mendeli törvények Mendel előtt és körül A genetika törvényeinek újbóli felfedezése és a kromoszómák Watson és Crick a molekuláris biológoa központi dogmája 10.2.2010
10.2.2010 genmisk1 1 Áttekintés Mendel és a mendeli törvények Mendel előtt és körül A genetika törvényeinek újbóli felfedezése és a kromoszómák Watson és Crick a molekuláris biológoa központi dogmája 10.2.2010
A Hardy Weinberg-modell gyakorlati alkalmazása
 1 of 6 5/16/2009 2:59 PM A Hardy Weinberg-modell gyakorlati alkalmazása A genotípus-gyakoriság megoszlásának vizsgálata 1. ábra. A Hardy Weinberg-egyensúlyi genotípus-gyakoriságok az allélgyakoriság Számos
1 of 6 5/16/2009 2:59 PM A Hardy Weinberg-modell gyakorlati alkalmazása A genotípus-gyakoriság megoszlásának vizsgálata 1. ábra. A Hardy Weinberg-egyensúlyi genotípus-gyakoriságok az allélgyakoriság Számos
Ütemezési problémák. Kis Tamás 1. ELTE Problémamegoldó Szeminárium, ősz 1 MTA SZTAKI. valamint ELTE, Operációkutatási Tanszék
 Ütemezési problémák Kis Tamás 1 1 MTA SZTAKI valamint ELTE, Operációkutatási Tanszék ELTE Problémamegoldó Szeminárium, 2012. ősz Kivonat Alapfogalmak Mit is értünk ütemezésen? Gépütemezés 1 L max 1 rm
Ütemezési problémák Kis Tamás 1 1 MTA SZTAKI valamint ELTE, Operációkutatási Tanszék ELTE Problémamegoldó Szeminárium, 2012. ősz Kivonat Alapfogalmak Mit is értünk ütemezésen? Gépütemezés 1 L max 1 rm
3. Általános egészségügyi ismeretek az egyes témákhoz kapcsolódóan
 11. évfolyam BIOLÓGIA 1. Az emberi test szabályozása Idegi szabályozás Hormonális szabályozás 2. Az érzékelés Szaglás, tapintás, látás, íz érzéklés, 3. Általános egészségügyi ismeretek az egyes témákhoz
11. évfolyam BIOLÓGIA 1. Az emberi test szabályozása Idegi szabályozás Hormonális szabályozás 2. Az érzékelés Szaglás, tapintás, látás, íz érzéklés, 3. Általános egészségügyi ismeretek az egyes témákhoz
Az Informatika Elméleti Alapjai
 Az Informatika Elméleti Alapjai dr. Kutor László Az üzenet információ-tartalma, redundanciája Minimális redundanciájú kódok http://mobil.nik.bmf.hu/tantárgyak/iea.html Felhasználónév: iea Jelszó: IEA07
Az Informatika Elméleti Alapjai dr. Kutor László Az üzenet információ-tartalma, redundanciája Minimális redundanciájú kódok http://mobil.nik.bmf.hu/tantárgyak/iea.html Felhasználónév: iea Jelszó: IEA07
ÁLLATTENYÉSZTÉSI GENETIKA
 TÁMOP-4.1.2-08/1/A-2009-0010 project ÁLLATTENYÉSZTÉSI GENETIKA University of Debrecen University of West Hungary University of Pannonia The project is supported by the European Union and co-financed by
TÁMOP-4.1.2-08/1/A-2009-0010 project ÁLLATTENYÉSZTÉSI GENETIKA University of Debrecen University of West Hungary University of Pannonia The project is supported by the European Union and co-financed by
Mire jó a modellalkotás? Jelenségek megmagyarázásának eszköze.
 Modellalkotás Mire jó a modellalkotás? Jelenségek megmagyarázásának eszköze. ok-okozati összefüggések feltárása összefüggések, mintázatok megmagyarázása "miért?" és "hogyan?" kérdések megválaszolása predikció
Modellalkotás Mire jó a modellalkotás? Jelenségek megmagyarázásának eszköze. ok-okozati összefüggések feltárása összefüggések, mintázatok megmagyarázása "miért?" és "hogyan?" kérdések megválaszolása predikció
Intelligens Rendszerek Elmélete
 Intelligens Rendszerek Elmélete Dr. Kutor László : Mesterséges neurális hálózatok felügyelt tanítása hiba visszateresztő Back error Propagation algoritmussal Versengéses tanulás http://mobil.nik.bmf.hu/tantargyak/ire.html
Intelligens Rendszerek Elmélete Dr. Kutor László : Mesterséges neurális hálózatok felügyelt tanítása hiba visszateresztő Back error Propagation algoritmussal Versengéses tanulás http://mobil.nik.bmf.hu/tantargyak/ire.html
Újrahasznosítási logisztika. 7. Gyűjtőrendszerek számítógépes tervezése
 Újrahasznosítási logisztika 7. Gyűjtőrendszerek számítógépes tervezése A tervezési módszer elemei gyűjtési régiók számának, lehatárolásának a meghatározása, régiónként az 1. fokozatú gyűjtőhelyek elhelyezésének
Újrahasznosítási logisztika 7. Gyűjtőrendszerek számítógépes tervezése A tervezési módszer elemei gyűjtési régiók számának, lehatárolásának a meghatározása, régiónként az 1. fokozatú gyűjtőhelyek elhelyezésének
Az Informatika Elméleti Alapjai
 Az Informatika Elméleti Alapjai Dr. Kutor László Az üzenet információ-tartalma és redundanciája Minimális redundanciájú kódok Statisztika alapú tömörítő algoritmusok http://mobil.nik.bmf.hu/tantargyak/iea.html
Az Informatika Elméleti Alapjai Dr. Kutor László Az üzenet információ-tartalma és redundanciája Minimális redundanciájú kódok Statisztika alapú tömörítő algoritmusok http://mobil.nik.bmf.hu/tantargyak/iea.html
FÜGGVÉNYEK TULAJDONSÁGAI, JELLEMZÉSI SZEMPONTJAI
 FÜGGVÉNYEK TULAJDONSÁGAI, JELLEMZÉSI SZEMPONTJAI FÜGGVÉNY: Adott két halmaz, H és K. Ha a H halmaz minden egyes eleméhez egyértelműen hozzárendeljük a K halmaznak egy-egy elemét, akkor a hozzárendelést
FÜGGVÉNYEK TULAJDONSÁGAI, JELLEMZÉSI SZEMPONTJAI FÜGGVÉNY: Adott két halmaz, H és K. Ha a H halmaz minden egyes eleméhez egyértelműen hozzárendeljük a K halmaznak egy-egy elemét, akkor a hozzárendelést
Heurisztikák algoritmusok ütemezési problémákra. 1. Állapottér és a megoldások kezelése
 Heurisztikák algoritmusok ütemezési problémákra 1. Állapottér és a megoldások kezelése Számos nehéz ütemezési probléma esetén az exponenciális idejű optimális megoldást adó algoritmusok rendkívül nagy
Heurisztikák algoritmusok ütemezési problémákra 1. Állapottér és a megoldások kezelése Számos nehéz ütemezési probléma esetén az exponenciális idejű optimális megoldást adó algoritmusok rendkívül nagy
Evolúció. Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet
 Evolúció Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet Mi az evolúció? Egy folyamat: az élőlények tulajdonságainak változása a környezethez való alkalmazkodásra Egy
Evolúció Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet Mi az evolúció? Egy folyamat: az élőlények tulajdonságainak változása a környezethez való alkalmazkodásra Egy
Tudománytörténeti visszatekintés
 GENETIKA I. AZ ÖRÖKLŐDÉS TÖRVÉNYSZERŰSÉGEI Minek köszönhető a biológiai sokféleség? Hogyan történik a tulajdonságok átörökítése? Tudománytörténeti visszatekintés 1. Keveredés alapú öröklődés: (1761-1766,
GENETIKA I. AZ ÖRÖKLŐDÉS TÖRVÉNYSZERŰSÉGEI Minek köszönhető a biológiai sokféleség? Hogyan történik a tulajdonságok átörökítése? Tudománytörténeti visszatekintés 1. Keveredés alapú öröklődés: (1761-1766,
[f(x) = x] (d) B f(x) = x 2 ; g(x) =?; g(f(x)) = x 1 + x 4 [
![[f(x) = x] (d) B f(x) = x 2 ; g(x) =?; g(f(x)) = x 1 + x 4 [ [f(x) = x] (d) B f(x) = x 2 ; g(x) =?; g(f(x)) = x 1 + x 4 [](/thumbs/94/119230405.jpg) Bodó Beáta 1 FÜGGVÉNYEK 1. Határozza meg a következő összetett függvényeket! g f = g(f(x)); f g = f(g(x)) (a) B f(x) = cos x + x 2 ; g(x) = x; f(g(x)) =?; g(f(x)) =? f(g(x)) = cos( x) + ( x) 2 = cos( x)
Bodó Beáta 1 FÜGGVÉNYEK 1. Határozza meg a következő összetett függvényeket! g f = g(f(x)); f g = f(g(x)) (a) B f(x) = cos x + x 2 ; g(x) = x; f(g(x)) =?; g(f(x)) =? f(g(x)) = cos( x) + ( x) 2 = cos( x)
A genetikai lelet értelmezése monogénes betegségekben
 A genetikai lelet értelmezése monogénes betegségekben Tory Kálmán Semmelweis Egyetem, I. sz. Gyermekklinika A ~20 ezer fehérje-kódoló gén a 23 pár kromoszómán A kromoszómán található bázisok száma: 250M
A genetikai lelet értelmezése monogénes betegségekben Tory Kálmán Semmelweis Egyetem, I. sz. Gyermekklinika A ~20 ezer fehérje-kódoló gén a 23 pár kromoszómán A kromoszómán található bázisok száma: 250M
Evolúciós alapfogalmak, általános algoritmusok
 MI2 előadás jegyzet Tartalom: - Evolúciós alapfogalmak, általános algoritmusok - Evolúciós stratégiák - Raj intelligencia, részecske-raj optimalizálás A jegyzetet Jelasity Márk 2008. 04. 08., 2008. 04.
MI2 előadás jegyzet Tartalom: - Evolúciós alapfogalmak, általános algoritmusok - Evolúciós stratégiák - Raj intelligencia, részecske-raj optimalizálás A jegyzetet Jelasity Márk 2008. 04. 08., 2008. 04.
Gépi tanulás a gyakorlatban. Lineáris regresszió
 Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2017/18 2. félév 3. Előadás Dr. Kulcsár Gyula egyetemi docens Kereső algoritmusok alkalmazása
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2017/18 2. félév 3. Előadás Dr. Kulcsár Gyula egyetemi docens Kereső algoritmusok alkalmazása
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
Statisztikai következtetések Nemlineáris regresszió Feladatok Vége
 [GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
[GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
E-tananyag Matematika 9. évfolyam 2014. Függvények
 Függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt a hozzárendelést
Függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt a hozzárendelést
Transzgénikus technológiák az orvostudományban A kövér egerektől a reumás betegségek gyógyításáig
 Transzgénikus technológiák az orvostudományban A kövér egerektől a reumás betegségek gyógyításáig ELTE TTK Biológiai Intézet Budapest, 2015. okt. 7. Dr. Mócsai Attila Semmelweis Egyetem ÁOK Élettani Intézet
Transzgénikus technológiák az orvostudományban A kövér egerektől a reumás betegségek gyógyításáig ELTE TTK Biológiai Intézet Budapest, 2015. okt. 7. Dr. Mócsai Attila Semmelweis Egyetem ÁOK Élettani Intézet
HÁROM KÖR A HÁROMSZÖGBEN
 Debreceni Egyetem Informatikai Kar HÁROM KÖR A HÁROMSZÖGBEN Konzulens: dr. Aszalós László egyetemi adjunktus Készítette: Király Péter programtervező matematikus szakos hallgató DEBRECEN, 008 Tartalomjegyzék
Debreceni Egyetem Informatikai Kar HÁROM KÖR A HÁROMSZÖGBEN Konzulens: dr. Aszalós László egyetemi adjunktus Készítette: Király Péter programtervező matematikus szakos hallgató DEBRECEN, 008 Tartalomjegyzék
Matematika 8. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Hat évfolyamos Matematika 8. osztály III. rész: Függvények Készítette: Balázs Ádám Budapest, 2018 2. Tartalomjegyzék Tartalomjegyzék III. rész:
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Hat évfolyamos Matematika 8. osztály III. rész: Függvények Készítette: Balázs Ádám Budapest, 2018 2. Tartalomjegyzék Tartalomjegyzék III. rész:
Kromoszómák, Gének centromer
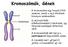 Kromoszómák, Gének A kromoszóma egy hosszú DNS szakasz, amely a sejt életének bizonyos szakaszában (a sejtosztódás előkészítéseként) tömörödik, így fénymikroszkóppal láthatóvá válik. A kromoszómák két
Kromoszómák, Gének A kromoszóma egy hosszú DNS szakasz, amely a sejt életének bizonyos szakaszában (a sejtosztódás előkészítéseként) tömörödik, így fénymikroszkóppal láthatóvá válik. A kromoszómák két
A kromoszómák kialakulása előtt a DNS állomány megkettőződik. A két azonos információ tartalmú DNS egymás mellé rendeződik és egy kromoszómát alkot.
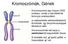 Kromoszómák, Gének A kromoszóma egy hosszú DNS szakasz, amely a sejt életének bizonyos szakaszában (a sejtosztódás előkészítéseként) tömörödik, így fénymikroszkóppal láthatóvá válik. A kromoszómák két
Kromoszómák, Gének A kromoszóma egy hosszú DNS szakasz, amely a sejt életének bizonyos szakaszában (a sejtosztódás előkészítéseként) tömörödik, így fénymikroszkóppal láthatóvá válik. A kromoszómák két
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén
 Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Biológiai feladatbank 12. évfolyam
 Biológiai feladatbank 12. évfolyam A pedagógus neve: A pedagógus szakja: Az iskola neve: Műveltségi terület: Tantárgy: A tantárgy cél és feladatrendszere: Tantárgyi kapcsolatok: Osztály: 12. Felhasznált
Biológiai feladatbank 12. évfolyam A pedagógus neve: A pedagógus szakja: Az iskola neve: Műveltségi terület: Tantárgy: A tantárgy cél és feladatrendszere: Tantárgyi kapcsolatok: Osztály: 12. Felhasznált
Mesterséges Intelligencia I. (I602, IB602)
 Dr. Jelasity Márk Mesterséges Intelligencia I. (I602, IB602) harmadik (2008. szeptember 15-i) előadásának jegyzete Készítette: Papp Tamás PATLACT.SZE KPM V. HEURISZTIKUS FÜGGVÉNYEK ELŐÁLLÍTÁSA Nagyon fontos
Dr. Jelasity Márk Mesterséges Intelligencia I. (I602, IB602) harmadik (2008. szeptember 15-i) előadásának jegyzete Készítette: Papp Tamás PATLACT.SZE KPM V. HEURISZTIKUS FÜGGVÉNYEK ELŐÁLLÍTÁSA Nagyon fontos
KUTATÁSMÓDSZERTAN 4. ELŐADÁS. A minta és mintavétel
 KUTATÁSMÓDSZERTAN 4. ELŐADÁS A minta és mintavétel 1 1. A MINTA ÉS A POPULÁCIÓ VISZONYA Populáció: tágabb halmaz, alapsokaság a vizsgálandó csoport egésze Minta: részhalmaz, az alapsokaság azon része,
KUTATÁSMÓDSZERTAN 4. ELŐADÁS A minta és mintavétel 1 1. A MINTA ÉS A POPULÁCIÓ VISZONYA Populáció: tágabb halmaz, alapsokaság a vizsgálandó csoport egésze Minta: részhalmaz, az alapsokaság azon része,
Csoportmódszer Függvények I. (rövidített változat) Kiss Károly
 Ismétlés Adott szempontok szerint tárgyak, élőlények, számok vagy fizikai mennyiségek halmazokba rendezhetők. A halmazok kapcsolatát pedig hozzárendelésnek (relációnak, leképezésnek) nevezzük. A hozzárendelés
Ismétlés Adott szempontok szerint tárgyak, élőlények, számok vagy fizikai mennyiségek halmazokba rendezhetők. A halmazok kapcsolatát pedig hozzárendelésnek (relációnak, leképezésnek) nevezzük. A hozzárendelés
függvény grafikonja milyen transzformációkkal származtatható az f0 : R R, f0(
 FÜGGVÉNYEK 1. (008. okt., 14. fel, 5+7 pont) Fogalmazza meg, hogy az f : R R, f ( x) x 1 függvény grafikonja milyen transzformációkkal származtatható az f0 : R R, f0( x) x függvény grafikonjából! Ábrázolja
FÜGGVÉNYEK 1. (008. okt., 14. fel, 5+7 pont) Fogalmazza meg, hogy az f : R R, f ( x) x 1 függvény grafikonja milyen transzformációkkal származtatható az f0 : R R, f0( x) x függvény grafikonjából! Ábrázolja
Statisztika I. 8. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34
 Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34. Meteorológiai Tudományos Napok Az előadás vázlata
Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34. Meteorológiai Tudományos Napok Az előadás vázlata
A sz.ot.ag. III. Magyar Számítógépes Nyelvészeti Konferencia december 8. Bíró Tamás, ELTE, Budapest / RUG, Groningen, NL 1/ 16
 A sz.ot.ag Optimalitáselmélet szimulált hőkezeléssel Bíró Tamás Humanities Computing, CLCG University of Groningen, Hollandia valamint Eötvös Loránd Tudományegyetem, Budapest birot@let.rug.nl, birot@nytud.hu
A sz.ot.ag Optimalitáselmélet szimulált hőkezeléssel Bíró Tamás Humanities Computing, CLCG University of Groningen, Hollandia valamint Eötvös Loránd Tudományegyetem, Budapest birot@let.rug.nl, birot@nytud.hu
2012. október 2 és 4. Dr. Vincze Szilvia
 2012. október 2 és 4. Dr. Vincze Szilvia Tartalomjegyzék 1.) Az egyváltozós valós függvény fogalma, műveletek 2.) Zérushely, polinomok zérushelye 3.) Korlátosság 4.) Monotonitás 5.) Szélsőérték 6.) Konvex
2012. október 2 és 4. Dr. Vincze Szilvia Tartalomjegyzék 1.) Az egyváltozós valós függvény fogalma, műveletek 2.) Zérushely, polinomok zérushelye 3.) Korlátosság 4.) Monotonitás 5.) Szélsőérték 6.) Konvex
Mesterséges Intelligencia alapjai
 Mesterséges Intelligencia alapjai Evolúciós algoritmusok - neurális hálózatok Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék 2010 / Budapest
Mesterséges Intelligencia alapjai Evolúciós algoritmusok - neurális hálózatok Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék 2010 / Budapest
Kétszemélyes játékok
 Mesterséges Intelligencia alapjai, gyakorlat Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék 2010 / udapest Kétszemélyes teljes információjú játékok két
Mesterséges Intelligencia alapjai, gyakorlat Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék 2010 / udapest Kétszemélyes teljes információjú játékok két
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Genetikus algoritmusok megvalósítása MATLAB segítségével
 Genetikus algoritmusok megvalósítása MATLAB segítségével Werner Ágnes A Matlab genetikus algoritmusokat használó eszköztára Kétféle módon használhatjuk fel az eszköztár lehetőségeit: 1. Parancssorból 2.
Genetikus algoritmusok megvalósítása MATLAB segítségével Werner Ágnes A Matlab genetikus algoritmusokat használó eszköztára Kétféle módon használhatjuk fel az eszköztár lehetőségeit: 1. Parancssorból 2.
A genetikai sodródás
 A genetikai sodródás irányított, nem véletlenszerű Mindig a jobb nyer! természetes szelekció POPULÁCIÓ evolúció POPULÁCIÓ A kulcsszó: változékonyság a populáción belül POPULÁCIÓ nem irányított, véletlenszerű
A genetikai sodródás irányított, nem véletlenszerű Mindig a jobb nyer! természetes szelekció POPULÁCIÓ evolúció POPULÁCIÓ A kulcsszó: változékonyság a populáción belül POPULÁCIÓ nem irányított, véletlenszerű
A vérképző rendszerben ionizáló sugárzás által okozott mutációk kialakulásának numerikus modellezése
 A vérképző rendszerben ionizáló sugárzás által okozott mutációk kialakulásának numerikus modellezése Madas Balázs Gergely XXXIX. Sugárvédelmi Továbbképző Tanfolyam Hajdúszoboszló, Hunguest Hotel Béke 2014.
A vérképző rendszerben ionizáló sugárzás által okozott mutációk kialakulásának numerikus modellezése Madas Balázs Gergely XXXIX. Sugárvédelmi Továbbképző Tanfolyam Hajdúszoboszló, Hunguest Hotel Béke 2014.
Paleobiológiai módszerek és modellek 11. hét
 Paleobiológiai módszerek és modellek 11. hét A diverzitás fajtái és mérőszámai Nagy őslénytani adatbázisok: Sepkoski The Fossil Record Paleobiology Database A diverzitás fogalma Diverzitás sokféleség az
Paleobiológiai módszerek és modellek 11. hét A diverzitás fajtái és mérőszámai Nagy őslénytani adatbázisok: Sepkoski The Fossil Record Paleobiology Database A diverzitás fogalma Diverzitás sokféleség az
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
Felvételi tematika INFORMATIKA
 Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Függvények 1. oldal Készítette: Ernyei Kitti. Függvények
 Függvények 1. oldal Készítette: Ernyei Kitti Függvények DEFINÍCIÓ: Ha adott két nemüres halmaz: és, továbbá minden eleméhez hozzárendeljük a valamely elemét, akkor ezt a hozzárendelést függvénynek nevezzük.
Függvények 1. oldal Készítette: Ernyei Kitti Függvények DEFINÍCIÓ: Ha adott két nemüres halmaz: és, továbbá minden eleméhez hozzárendeljük a valamely elemét, akkor ezt a hozzárendelést függvénynek nevezzük.
Universität M Mis is k k olol ci c, F Eg a y kultä etem t, für Wi Gazda rts ságcha tudft o sw máis n s yen i scha Kar, ften,
 9. Előadás 1. Genetikus algoritmusok közgazdasági alkalmazása 2. Ökológiai és evolúciós közgazdaságtan Universität Miskolc, Fakultät für Wirtschaftswissenschaften, Istitut für Wirtschaftstheorie Miskolci
9. Előadás 1. Genetikus algoritmusok közgazdasági alkalmazása 2. Ökológiai és evolúciós közgazdaságtan Universität Miskolc, Fakultät für Wirtschaftswissenschaften, Istitut für Wirtschaftstheorie Miskolci
