Latin négyzetek alkalmazásai a titkosításban
|
|
|
- Petra Bakos
- 7 évvel ezelőtt
- Látták:
Átírás
1 Latin négyzetek alkalmazásai a titkosításban DÉNES TAMÁS tdenest@fre .hu Kulcsszavak: korai módszerek, latin négyzetek tulajdonságai, kódfejtés A rejtjelzô rács figyelemreméltó divattá vált évszázadokon keresztül a kriptográfiában. A Cardano-rács történetét és alkalmazását a titkosításban e folyóirat már közölte [5], ezért jelen dolgozatom a permutációs mátrixokkal és latin négyzetekkel való kapcsolatát mutatja be, amely egyúttal rávilágít eme 450 éves találmány 21. századi rendkívüli lehetôségeire. A digitális technika új perspektívákat nyit a sztegonográfiának és ezen belül a rejtjelzô rácsoknak is. Girolamo Cardano ( ) korszakos és mai napig ható módszercsaládja amely a sztegonográfia [6] új ágát indította útjára, a róla elnevezett Cardanorács. Tulajdonképpen egy betûmátrixra helyezhetô sablonról van szó. A pontosabb megértéshez idézzük fel magának Cardanonak a szavait: Végy két azonos méretû pergamen lapot és azonos vonalak mentén készíts kivágásokat különbözô helyeken. Ezek a kivágások legyenek kicsik, de mégis legalább akkorák, mint az ABC nagybetûi. Az összes kivágásokba összesen 120 betût lehessen elhelyezni. Az egyik pergamen lapot majd a levelezô társadnak adod. Amikor alkalom adódik, elôször írd az üzenetedet olyan tömören, ahogy csak lehetséges, így az üzenet kevesebb betût is tartalmazhat, mint amennyi a kivágott ablakokban elhelyezhetô. Amikor beírtad az üzeneted az egyik pergamen lapra, tedd ugyanezt a másikkal is. Ezután töltsd ki az elsô lapon az üresen maradt helyet úgy, hogy teljes mondatokra egészítsék ki a már ráirt szöveget. Ez a kitöltés úgy történjen, hogy a teljes szöveg stílusa és tartalma összefüggô és egységes legyen. Amikor a levelezô társad megkapja a te üzenetedet, ráhelyezi a megfelelô kivágásokkal ellátott pergament és így elolvashatja az üzenetet. Latin négyzetek és permutációs mátrixok kapcsolata Egy P(n) nxn-es, (0,1)-es mátrixot permutációs mátrixnak nevezünk, ha a mátrix pontosan n darab 1-t tartalmaz úgy, hogy minden sorban és oszlopban pontosan egy darab 1 lehet, a többi elem nulla. Érdekes és a rejtjelzô-rácsok szempontjából fontos eredmény az alábbi: Egy L(n) nxn-es latin négyzet kölcsönösen-egyértelmûen felbontható n darab permutációs mátrix összegére [2,3], azaz L(n) = 1 P i1 + 2 P i n P in (1) ahol P ik az i k -adik permutációs mátrix, azaz a mátrixban 1 szerepel mindenhol, ahol L(n)-ben k van, a mátrix többi eleme nulla. (A + összeadás mûvelet a mátrixok összeadását, míg a szorzás a mátrixok skalár szorzását jelöli.) Ezen megfeleltetések következménye, hogy az így adódó permutációs mátrixok jól felhasználhatók rejtjelzô rácsként. A következô szemléltetô példában a (2)- beli L(4) latin négyzet P 1, P 2, P 3, P 4 permutációs mátrixokra való egyértelmû felbontása látható: (2) (3) A rejtjelzô rács tulajdonképpen egy betûkeverési rejtjelzô eszköz, amely az úgynevezett nyílt szöveg betûit egy betûmátrixba képezi le. Mindegyik P i permutációs mátrix egy rejtjelzô rácsként fogható fel, ahol az 1- esek helyén ablakok vannak. Példaként legyen a nyílt szöveg a SZIA és használjuk a P 1 permutációs mátrixot rejtjelzô rácsként. Ekkor egy tetszôleges B 4x4-es betûmátrixban hagyjuk üresen azokat a cellákat, ahol P 1 -ben 1-es van (ezek a rejtô ablakok ). Majd az ablakokba balról-jobbra, fentrôl-lefelé írjuk be a nyílt szöveget, így kapjuk a P 1 -nek megfelelô ráccsal rejtjelzett B 1 betûmátrixot. Így a permutációs mátrixok (mint rácsok) egymás utáni betûmátrixra helyezésével tudjuk a kívánt szöveget a betûmátrixba írni és a fordított eljárással kiolvas- (4) (5) 46 LX. ÉVFOLYAM 2005/3
2 Latin négyzetek alkalmazásai a titkosításban ni. Mivel a latin négyzetekre vonatkozó fenti egyértelmû felbontási tétel miatt az így készített rácsok ablakai pontosan lefedik a betûmátrix n 2 mezôjét, ezzel a módszerrel elértük, hogy a teljes betûmátrixot kitölthetjük rejtett szöveggel. További elôny, hogy a latin négyzet felbontásának egyértelmûsége nem sérül, ha a felbontást adó permutációs mátrixok (rácsok) sorrendjét megváltoztatjuk. Így a felbontások számának n!-szorosa a lehetséges rácsfelhasználások száma. A rejtjelzésben a kulcstér mérete is fontos tényezô, ezért igen érdekesek a latin négyzetek számára vonatkozó eredmények. Az L(n) nxn-es latin négyzetek permutációs mátrixokra való felbontásainak száma megegyezik az összes nxn-es latin négyzetek számával. A latin négyzetek számára pontos formula egyelôre nem létezik, azt azonban tudjuk, hogy ha T n -nel jelöljük az úgynevezett redukált nxn-es latin négyzetek számát (redukált latin négyzet, melynek elsô sora és oszlopa az 1,2,...,n természetes számokat alapsorrendben tartalmazza), akkor T n (n 2)!(n 3)!...(2!)(1!), míg az összes nxn-es latin négyzetek számára fennáll az U n =n!(n-1)! T n összefüggés. A redukált latin négyzetek számának pontos értékét eddig csupán n=10-ig sikerült számítógéppel meghatározni, hogy mekkora számokról van szó, annak illusztrálására álljon itt T 9 = [1]. Ez a szám kb. 38 milliószorosa a Földön ma élô emberiség létszámának. A rejtjelzésben javasolható rácsméretek az 20 n 30 értékek! A következôkben megmutatjuk, hogy a permutációs mátrixok (és bizonyos feltételek mellett a latin négyzetek is) megsorszámozhatók, azaz az nxn-es permutációs mátrixok és az 1, 2,..., n! természetes számok között kölcsönösen egyértelmû megfeleltetés létesíthetô. Az 1.,2.,3. tételek bizonyítása megtalálható [4]-ben. 1.Tétel Bármely P i nxn-es permutációs mátrixhoz kölcsönösen egyértelmûen hozzárendelhetô egy p i n-edfokú permutáció. Az 1.tétel illusztrálásához lássuk el a (3)-beli P 1 permutációs mátrixot perem elemekkel. Ekkor a (6) mátrixot kapjuk. A P 1 permutációs mátrixhoz rendeljük a p 1 permutációt a következôképpen: A P 1 mátrix elsô sorában található 1-hez tartozó vízszintes és függôleges perem elemeket írjuk egymás alá, ez lesz a p 1 permutáció elsô oszlopa. Tegyük ugyanezt a P 1 mátrix második, harmadik, negyedik sorával, így kapjuk a p 1 permutáció megfelelô oszlopait, azaz, ha P(i,j)=1, akkor p 1 megfelelô oszlopa ( i j) (lásd a (7) levezetést). (6) Permutációk és a faktoriális alapú számrendszer Ahhoz, hogy a permutációs mátrixokhoz sorszámot rendeljünk, az 1.tétel alapján elegendô a permutációk megsorszámozása. Erre ad módot a következô 2. és 3. tétel. 2. Tétel ( faktoriális alapú számrendszer) Legyenek m és b i természetes számok, melyekre teljesül, hogy 1 m n! (8) 0 b i i 1 (i=1,2,3,...,n) (9) (7) (10) Ekkor bármely (8)-nak megfelelô m-hez pontosan egy b i sorozat létezik, amely eleget tesz a (9), (10) összefüggéseknek. Amint azt láttuk, az összes n-ed rendû latin négyzet elôállítása teljesen megoldatlan probléma, hiszen akkor egyúttal megoldódna a leszámlálásuk is, de n 10 esetén még az összes latin négyzetek pontos számát sem ismerjük. Így a latin négyzetek alkalmazása szempontjából különleges jelentôsége van, ha bizonyos típusú latin négyzet osztályok elôállítására tudunk algoritmust adni, fôleg ha ez egyszerre a természetes számokhoz való egyértelmû hozzárendelést is jelent. Ekkor ugyanis a rejtjelzésben jelentôs véletlenszám generátorok felhasználására is mód nyílik, másrészt tárolási és továbbítási elônye van. A következôkben olyan latin négyzet osztályt állítunk elô, amelynek soraiban lévô permutációk elemi transzpozíciókkal származtathatók egymásból. Az algoritmus részletes leírása [4]-ben megtalálható. Az eljárás elemi transzpozíciók segítségével állítja elô a permutációkat. Legyen a kiindulási permutáció (a π 1 kezdôpermutáció megválasztása tetszôleges lehet): Ekkor a rekurziós formula a következô: (11) (12) σ m meghatározásához soroljuk a természetes számokat az A 1,A 2,...,A k osztályokba úgy, hogy és (13) (14) A σ m transzpozíció szorzatot a továbbiakban σ m transzformációnak nevezzük. A τ i jelölés elemi transzpozíciót jelöl, azaz τ i =(i i+1), így (14) a következôképpen írható: LX. ÉVFOLYAM 2005/3 47
3 HÍRADÁSTECHNIKA (15) Az eljárás tehát a következô transzformáció-szorzatot állítja elô: (16) Osztályozzuk a transzformációkat az indexük szerint, vagyis σ r és σ s akkor és csak akkor tartozik egy osztályba, ha r és s a (13) definíció szerint egy osztályba tartozik. Ekkor könnyen belátható, hogy az egy osztályba tartozó transzformációk egyenlôk, hiszen r és s egyértelmûen határozzák meg a (15) definíció k osztályindexét. A (13)-(16) osztályozási definíciók és a transzformációk egyenlôsége miatt igaz a következô: K3.2. Másrészrôl (17) minden sora különbözô latin négyzetet állít elô, így a fenti rekurzív eljárással (n-1)! latin négyzet könnyen elôállítható. K3.3. A K3.1. következménybôl adódik, hogy az így generált latin négyzetek reprezentálhatók a megfelelô sor kezdôpermutációjával. Azaz a kezdôpermutációhoz rendelt sorszámmal azonosíthatók. A fentiekben bevezetett jelölésekkel az alábbi sorszámozott latin négyzeteket kapjuk: (21) (17) Példa: n=4, m=3 (lásd az 1. táblázatot) Helyettesítsük be (16)-ba a (17) egyenlôségrendszerben kapottakat: (18) Mivel a transzformáció szorzat nem más, mint az összes (n-1)-ed fokú permutációk elôállításához szükséges transzformációk szorzata, vezessük be a következô egyszerûbb jelölést: (19) Ahol tehát ρ r az összes r-ed fokú permutáció elôállításához szükséges transzformációk szorzatát jelöli. Ekkor (18) így írható: Latin négyzetek megszámozása (20) (22) Az (1) felbontásnak megfelelôen permutációs mátrixok összegeként felírva: Példa: n=4, m=3 (lásd az 1. táblázatot) (23) (24) 3. Tétel A (20) formula n! különbözô permutációt állít elô. Következmények: K3.1. A 3. tétel következményeként adódik, hogy a (17) egyenlôségrendszer minden sorának elsô eleme különbözô permutációt állít elô. Az egy sorban levô transzformációk a teljes n-edfokú ciklus (C n ) különbözô hatványaival szorozzák a sor elsô (kezdô) permutációját, így ezek is különbözôek és teljes ciklust alkotnak. Ebbôl következik, hogy (17) minden sora n darab olyan permutációt generál, amelyek egy latin négyzetet alkotnak. Latin négyzet alapú rejtjelzés (25) Használjuk a példa permutációs mátrixait rejtjelzô-rácsként. Legyen a nyílt szöveg: AMI TITOK AZ TITOK! és legyen a rácsok sorrendje a fenti (3, 9, 15, 21), ekkor a rejtett betûmátrix a következô (26): 48 LX. ÉVFOLYAM 2005/3
4 Latin négyzetek alkalmazásai a titkosításban Latin négyzet alapú digitális aláírás Mint azt megjegyeztük, ugyanezzel a négy ráccsal 4!=24-féleképpen állíthatjuk elô a rejtett betûmátrixot. Példaként bemutatjuk a 15, 3, 21, 9 sorrendhez tartozó betûmátrixot is (27): A fenti rekurziós algoritmus az összes n-edfokú permutációknak egy egymásbaskatulyázott blokkos elrendezését adja (1.táblázat), amelyre teljesülnek az alábbiak: A1) Minden blokk utolsó oszlopában azonos elemek vannak. A2) Azonos fokszámú, de különbözô blokkok utolsó oszlopai különbözôk. A3) Az A1., A2. tulajdonságokból következik, hogy egy tetszôleges n-edfokú permutáció minden eleme egyértelmûen meghatároz egy blokkot, mégpedig az a i elem egy (i-1)-edfokú blokkot, amelyhez hozzárendelhetjük a (9) szerinti b i értéket. Az így nyert b i (i=1,2,...,n) sorozat (10) szerint egyértelmûen rendeli a permutációhoz az m természetes számot. 1. táblázat Ha a permutációs mátrixokat rejtjelzô-rácsként alkalmazzuk, akkor a P i mátrix, illetve az ehhez tartozó p i permutáció helyett elegendô az i szám tárolása az azonosításhoz. Egy n-ed fokú permutáció tárolásához (csak a képelemeket tároljuk!) c(n) számú karakterre van szükség, ahol (28) Az n! szám számjegyeinek száma (jelöljük j(n)-nel): (29) Ekkor bár fennáll, hogy (30) Az elektronikus pénz átutalás (EFT=Electronic Fund Transfer) és általában az elektronikus posta elterjedése felvetette a hagyományos aláírás helyettesítését digitálisan elôállított (kódolt) elektronikus aláírással. A számítógépes terminálok használóinak, vagy az adatbankokhoz való hozzáférés jogosságának ellenôrzésénél hasonló problémákat kell megoldani, mint a hagyományos levél, illetve más papíralapú dokumentumok hitelesítésénél, ahol ezt a célt szolgálta a kézi aláírás. Nyilvánvaló, hogy egy digitális, teljesen elektronizált rendszerben a kézi hitelesítést is helyettesíteni kell, erre való a digitális aláírás, amely azonban olyan kódolási módszereket használ, amelyek nem csupán a dokumentum aláíróját, hanem a dokumentum tartalmát is hitelesítik. Sok módszer ismeretes a digitális aláírás megvalósítására. Most egy olyan eljárást mutatok be, amely latin négyzeteken alapul és közvetlenül alkalmas párhuzamos mûködésû számítógépen való implementálásra, ami rendkívüli módon megnöveli a mûködési sebességet. Legyen adott egy U=a 1,a 2,...,a n üzenet ahol az üzenet betûi (a i ) egy q elemû ábécébôl valók. Az üzenet hitelesítését (digitális aláírását) az üzenettel azonos ábécé-bôl vett s darab (A=b 1,b 2,...,b s ) betûvel kívánjuk elvégezni. Tegyük fel az egyszerûség kedvéért, hogy n osztható s-sel, vagyis n=s t. Válasszuk szét az üzenetet s darab részüzenetre (a szétválasztás egy kulcs szerint fog történni, ami esetünkben egy latin négyzet). Minden részüzenet t darab betûbôl fog állni és minden egyes részüzenet az elektronikus aláírás egy betûjét határozza meg. Az eljárást egy példán fogom szemléltetni, amely a könnyebb áttekinthetôség érdekében kis n és q értékekre vonatkozik. Legyen az üzenet U= (vagyis n=16, q=4, s=4). A kulcs amely szerint az üzenetet részüzenetekre bontjuk egy s-ed rendû (jelen esetben 4-ed rendû) latin négyzet: (32) 2. táblázat amelyre (31) mégis a gyakorlatban ez a megfeleltetés jól használható, mivel az általában használatos 10 n 500 értékekre a 2. táblázat (jobbra) értékei adódnak, ami azt mutatja, hogy 25-50% helymegtakarítást érhetünk el. j(n) n j(n) c(n) c(n) LX. ÉVFOLYAM 2005/3 49
5 HÍRADÁSTECHNIKA A (33) mátrix egy segédtáblázat, amelynek felhasználása a következôkben kerül ismertetésre. (33) A fenti eljárás teljesen egyértelmû eredményre vezet, hiszen az U üzenet felbontása részüzenetekre a latin négyzet elemeinek diszjunkt osztályozásán alapul, ez viszont a fentiekben ismertetett permutációs mátrixokra való felbontási tétel miatt kölcsönösen egyértelmû. A latin négyzeteken alapuló mûvelettáblák nem aszszociatív algebrai struktúrát (úgynevezett kvázicsoportot) reprezentálnak, aminek nagy jelentôsége van az illetéktelen hamisítás elleni védekezésnél, mivel két karakter egyszerû felcserélését is kimutatja. Ezzel a képességgel a paritás ellenôrzésen alapuló módszerek, vagy a numerikus eljárások nem rendelkeznek. Az U üzenet U 1, U 2, U 3,..., U s részüzenetekre való bontásának lépései a következôk: Válasszuk ki a (32) latin négyzetben szereplô azonos elemek sorszámát a (33) mátrix szerint úgy, hogy például a 0 elemekhez tartozó sorszámok a (33) mátrix ráhelyezésével a következôknek adódnak: 1, 7, 12, 14. Ugyanezt az eljárást alkalmazva a (32) latin négyzet 1- es, 2-es és 3-as elemeire is, a sorszámokat négy osztályba osztjuk: (1, 7, 12, 14), (4, 6, 9, 15), (2, 5, 11, 16), (3, 7, 9, 13). Ezután a sorszámokat (megtartva az osztályozást) helyettesítjük az U üzenetnek az illetô sorszám szerinti helyén álló elemével. Így a következô kevert részüzeneteket kapjuk: U 1 = (1, 3, 3, 0), U 2 = (2, 0, 0, 0), U 3 = (0, 2, 2, 3), U 4 = (3, 1, 1, 1). Most lássuk el a (32) latin négyzetet perem elemekkel: (34) Így tulajdonképpen a (0,1,2,3) halmazon definiáltunk egy * mûveletet, amelynek mûvelettáblája a (34) latin négyzet. A (34) mûvelettáblát pontosan úgy használjuk, mint a jól ismert szorzótáblát, például azt kapjuk, hogy 0*1=2, 1*2=0, stb. A nem matematikus olvasó számára talán szokatlan, hogy a * mûvelet nem asszociatív, vagyis a*(b*c) (a*b)*c, azaz például 2*(3*1)=2*0=1, de (2*3)*1=0*1=2, vagyis 2*(3*1) (2*3)*1. Ennek a tulajdonságnak nagy jelentôsége van a következôkben bemutatott kódolási eljárásnál. A példánkban szereplô U üzenet digitális aláírásához az egyes U 1, U 2, U 3, U 4 részüzenetek szorzatát kell elôállítani a (34) mûvelettábla alapján: Záró megjegyzés Végül szeretném felhívni az olvasó figyelmét arra, hogy a rejtjelzés, hitelesítés, illetve a digitális aláírás numerikus módszereinek biztonsága (feltörhetôsége) alapvetôen függ a pillanatnyi számítástechnikai eszközök kapacitásától. Azaz a feltörhetetlenség mellett szóló érvek, a több ezer éves számolási igény a rejtett kulcsok megfejtéséhez, a gyors hardver fejlôdéssel bizonytalanná válnak. Bízom benne, hogy a latin négyzetek titkosítási alkalmazásainak e vázlatos ismertetésébôl egyértelmûen kitûnik, hogy a latin négyzeteken alapuló strukturális módszerrel aláírt és rejtjelzett elektronikus dokumentumok esetén nem kell tartani a számítógépek sebesség és kapacitás növekedésétôl. Irodalom [1] J. Dénes, A.D. Keedwell: Latin squares and their applications, Akadémiai Kiadó, Budapest, [2] J. Dénes, A.D. Keedwell: Latin squares and 1-factorizations of complete graphs, I. Ars Combinatorica, 25A (1988), pp [3] J. Dénes, A.D. Keedwell: Latin squares and 1-factorizations of complete graphs, II. Utilitas Math., 34 (1988), pp [4] Dénes Tamás: Algoritmusok az összes n-edfokú permutáció elôállítására, I.-II. Információ Elektronika, 1975/1.-2. [5] Dénes Tamás: A rejtjelzô rácsok születése Híradástechnika, 2001/10, pp [6] Dénes Tamás: SZTEGONOGRÁFIA rejtett információk rejtjelzés nélkül Híradástechnika, 2001/8, pp (35) vagyis az U üzenethez tartozó hitelesítô aláírás: A=(b 1 b 2 b 3 b 4 )= LX. ÉVFOLYAM 2005/3
Lineáris algebra (10A103)
 Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
1. előadás: Halmazelmélet, számfogalom, teljes
 1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy
 1. előadás: Halmazelmélet Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy hozzátartozik-e,
1. előadás: Halmazelmélet Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy hozzátartozik-e,
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
 Az RSA módszer Az RSA módszer titkossága a prímtényezős felbontás nehézségén, a prímtényezők megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
Az RSA módszer Az RSA módszer titkossága a prímtényezős felbontás nehézségén, a prímtényezők megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
Hadamard-mátrixok Előadó: Hajnal Péter február 23.
 Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
I. VEKTOROK, MÁTRIXOK
 217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
Algebra es sz amelm elet 3 el oad as Permut aci ok Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Permutációk Waldhauser Tamás 2014 őszi félév 1. Definíció. Permutációnak nevezzük egy nemüres (véges) halmaz önmagára való bijektív leképezését. 2. Definíció. Az {1, 2,...,
Algebra és számelmélet 3 előadás Permutációk Waldhauser Tamás 2014 őszi félév 1. Definíció. Permutációnak nevezzük egy nemüres (véges) halmaz önmagára való bijektív leképezését. 2. Definíció. Az {1, 2,...,
Műveletek mátrixokkal. Kalkulus. 2018/2019 ősz
 2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
OSZTHATÓSÁG. Osztók és többszörösök : a 3 többszörösei : a 4 többszörösei Ahol mindkét jel megtalálható a 12 többszöröseit találjuk.
 Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
1. Részcsoportok (1) C + R + Q + Z +. (2) C R Q. (3) Q nem részcsoportja C + -nak, mert más a művelet!
 1. Részcsoportok A részcsoport fogalma. 2.2.15. Definíció Legyen G csoport. A H G részhalmaz részcsoport, ha maga is csoport G műveleteire nézve. Jele: H G. Az altér fogalmához hasonlít. Példák (1) C +
1. Részcsoportok A részcsoport fogalma. 2.2.15. Definíció Legyen G csoport. A H G részhalmaz részcsoport, ha maga is csoport G műveleteire nézve. Jele: H G. Az altér fogalmához hasonlít. Példák (1) C +
Mátrixok, mátrixműveletek
 Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Leképezések. Leképezések tulajdonságai. Számosságok.
 Leképezések Leképezések tulajdonságai. Számosságok. 1. Leképezések tulajdonságai A továbbiakban legyen A és B két tetszőleges halmaz. Idézzünk fel néhány definíciót. 1. Definíció (Emlékeztető). Relációknak
Leképezések Leképezések tulajdonságai. Számosságok. 1. Leképezések tulajdonságai A továbbiakban legyen A és B két tetszőleges halmaz. Idézzünk fel néhány definíciót. 1. Definíció (Emlékeztető). Relációknak
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Elemi matematika szakkör
 Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
Diszkrét matematika I., 12. előadás Dr. Takách Géza NyME FMK Informatikai Intézet takach november 30.
 1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
II. Két speciális Fibonacci sorozat, szinguláris elemek, természetes indexelés
 II. Két speciális Fibonacci sorozat, szinguláris elemek, természetes indexelés Nagyon könnyen megfigyelhetjük, hogy akármilyen két számmal elindítunk egy Fibonacci sorozatot, a sorozat egymást követő tagjainak
II. Két speciális Fibonacci sorozat, szinguláris elemek, természetes indexelés Nagyon könnyen megfigyelhetjük, hogy akármilyen két számmal elindítunk egy Fibonacci sorozatot, a sorozat egymást követő tagjainak
Fraktálok. Kontrakciók Affin leképezések. Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék. TARTALOMJEGYZÉK Kontrakciók Affin transzformációk
 Fraktálok Kontrakciók Affin leképezések Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 71 A Lipschitz tulajdonság ÁTMÉRŐ, PONT ÉS HALMAZ TÁVOLSÁGA Definíció Az (S, ρ) metrikus tér
Fraktálok Kontrakciók Affin leképezések Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 71 A Lipschitz tulajdonság ÁTMÉRŐ, PONT ÉS HALMAZ TÁVOLSÁGA Definíció Az (S, ρ) metrikus tér
A továbbiakban Y = {0, 1}, azaz minden szóhoz egy bináris sorozatot rendelünk
 1. Kódelmélet Legyen X = {x 1,..., x n } egy véges, nemüres halmaz. X-et ábécének, elemeit betűknek hívjuk. Az X elemeiből képzett v = y 1... y m sorozatokat X feletti szavaknak nevezzük; egy szó hosszán
1. Kódelmélet Legyen X = {x 1,..., x n } egy véges, nemüres halmaz. X-et ábécének, elemeit betűknek hívjuk. Az X elemeiből képzett v = y 1... y m sorozatokat X feletti szavaknak nevezzük; egy szó hosszán
24. szakkör (Csoportelméleti alapfogalmak 3.)
 24. szakkör (Csoportelméleti alapfogalmak 3.) D) PERMUTÁCIÓK RENDJE Fontos kérdés a csoportelméletben, hogy egy adott elem hanyadik hatványa lesz az egység. DEFINÍCIÓ: A legkisebb olyan pozitív k számot,
24. szakkör (Csoportelméleti alapfogalmak 3.) D) PERMUTÁCIÓK RENDJE Fontos kérdés a csoportelméletben, hogy egy adott elem hanyadik hatványa lesz az egység. DEFINÍCIÓ: A legkisebb olyan pozitív k számot,
A 2015/2016. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló MATEMATIKA III. KATEGÓRIA (a speciális tanterv szerint haladó gimnazisták)
 A 205/206. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló MATEMATIKA III. KATEGÓRIA a speciális tanterv szerint haladó gimnazisták Javítási-értékelési útmutató. feladat Az {,2,...,n} halmaz
A 205/206. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló MATEMATIKA III. KATEGÓRIA a speciális tanterv szerint haladó gimnazisták Javítási-értékelési útmutató. feladat Az {,2,...,n} halmaz
MBNK12: Permutációk (el adásvázlat, április 11.) Maróti Miklós
 MBNK12: Permutációk el adásvázlat 2016 április 11 Maróti Miklós 1 Deníció Az A halmaz permutációin a π : A A bijektív leképezéseket értjünk Tetsz leges n pozitív egészre az {1 n} halmaz összes permutációinak
MBNK12: Permutációk el adásvázlat 2016 április 11 Maróti Miklós 1 Deníció Az A halmaz permutációin a π : A A bijektív leképezéseket értjünk Tetsz leges n pozitív egészre az {1 n} halmaz összes permutációinak
44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY. Megyei forduló április 11.
 44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló - 2015. április 11. HETEDIK OSZTÁLY - Javítási útmutató 1. Ki lehet-e tölteni a következő táblázat mezőit pozitív egész számokkal úgy, hogy
44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló - 2015. április 11. HETEDIK OSZTÁLY - Javítási útmutató 1. Ki lehet-e tölteni a következő táblázat mezőit pozitív egész számokkal úgy, hogy
Diszkrét matematika 1.
 Diszkrét matematika 1. 201. ősz 1. Diszkrét matematika 1. 1. előadás Mérai László diái alapján Komputeralgebra Tanszék 201. ősz Kombinatorika Diszkrét matematika 1. 201. ősz 2. Kombinatorika Kombinatorika
Diszkrét matematika 1. 201. ősz 1. Diszkrét matematika 1. 1. előadás Mérai László diái alapján Komputeralgebra Tanszék 201. ősz Kombinatorika Diszkrét matematika 1. 201. ősz 2. Kombinatorika Kombinatorika
Diszkrét matematika 2.
 Diszkrét matematika 2. 2018. november 23. 1. Diszkrét matematika 2. 9. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Komputeralgebra Tanszék 2018. november 23. Diszkrét matematika
Diszkrét matematika 2. 2018. november 23. 1. Diszkrét matematika 2. 9. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Komputeralgebra Tanszék 2018. november 23. Diszkrét matematika
Permutációk véges halmazon (el adásvázlat, február 12.)
 Permutációk véges halmazon el adásvázlat 2008 február 12 Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: ismétlés nélküli variáció leképezés indulási és érkezési halmaz
Permutációk véges halmazon el adásvázlat 2008 február 12 Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: ismétlés nélküli variáció leképezés indulási és érkezési halmaz
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Numerikus módszerek 1.
 Numerikus módszerek 1. 3. előadás: Mátrixok LU-felbontása Lócsi Levente ELTE IK 2013. szeptember 23. Tartalomjegyzék 1 Alsó háromszögmátrixok és Gauss-elimináció 2 Háromszögmátrixokról 3 LU-felbontás Gauss-eliminációval
Numerikus módszerek 1. 3. előadás: Mátrixok LU-felbontása Lócsi Levente ELTE IK 2013. szeptember 23. Tartalomjegyzék 1 Alsó háromszögmátrixok és Gauss-elimináció 2 Háromszögmátrixokról 3 LU-felbontás Gauss-eliminációval
Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József
 Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József Matematika III. 2. : Eseményalgebra Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel
Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József Matematika III. 2. : Eseményalgebra Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Függőleges. Vízszintes
 1. Fejtsd meg a rejtvényt! A főmegfejtés bizonyos karakterei a többi meghatározás egyes betűi alapján lesznek megfejthetőek. A meghatározásokat a lenti táblázatba írd, a megfelelő sorba. (10 pont a meghatározásokért
1. Fejtsd meg a rejtvényt! A főmegfejtés bizonyos karakterei a többi meghatározás egyes betűi alapján lesznek megfejthetőek. A meghatározásokat a lenti táblázatba írd, a megfelelő sorba. (10 pont a meghatározásokért
Alkalmazott modul: Programozás
 Eötvös Loránd Tudományegyetem Informatikai Kar Alkalmazott modul: Programozás Feladatgyűjtemény Összeállította: Giachetta Roberto groberto@inf.elte.hu http://people.inf.elte.hu/groberto Frissítve: 2015.
Eötvös Loránd Tudományegyetem Informatikai Kar Alkalmazott modul: Programozás Feladatgyűjtemény Összeállította: Giachetta Roberto groberto@inf.elte.hu http://people.inf.elte.hu/groberto Frissítve: 2015.
Acta Acad. Paed. Agriensis, Sectio Mathematicae 29 (2002) PARTÍCIÓK PÁRATLAN SZÁMOKKAL. Orosz Gyuláné (Eger, Hungary)
 Acta Acad. Paed. Agriensis, Sectio Mathematicae 9 (00) 07 4 PARTÍCIÓK PÁRATLAN SZÁMOKKAL Orosz Gyuláné (Eger, Hungary) Kiss Péter professzor emlékére Abstract. In this article, we characterize the odd-summing
Acta Acad. Paed. Agriensis, Sectio Mathematicae 9 (00) 07 4 PARTÍCIÓK PÁRATLAN SZÁMOKKAL Orosz Gyuláné (Eger, Hungary) Kiss Péter professzor emlékére Abstract. In this article, we characterize the odd-summing
1. Polinomfüggvények. Állítás Ha f, g C[x] és b C, akkor ( f + g) (b) = f (b) + g (b) és ( f g) (b) = f (b)g (b).
![1. Polinomfüggvények. Állítás Ha f, g C[x] és b C, akkor ( f + g) (b) = f (b) + g (b) és ( f g) (b) = f (b)g (b). 1. Polinomfüggvények. Állítás Ha f, g C[x] és b C, akkor ( f + g) (b) = f (b) + g (b) és ( f g) (b) = f (b)g (b).](/thumbs/92/110111081.jpg) 1. Polinomfüggvények Behelyettesés polinomba. Definíció Legyen b komplex szám. Az f (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n polinom b helyen felvett helyettesítési értéke f (b) = a 0 + a 1 b + a 2 b
1. Polinomfüggvények Behelyettesés polinomba. Definíció Legyen b komplex szám. Az f (x) = a 0 + a 1 x + a 2 x 2 +... + a n x n polinom b helyen felvett helyettesítési értéke f (b) = a 0 + a 1 b + a 2 b
Formális nyelvek és automaták
 Formális nyelvek és automaták Nagy Sára gyakorlatai alapján Készítette: Nagy Krisztián 2. gyakorlat Ismétlés: Megjegyzés: Az ismétlés egy része nem szerepel a dokumentumban, mivel lényegében a teljes 1.
Formális nyelvek és automaták Nagy Sára gyakorlatai alapján Készítette: Nagy Krisztián 2. gyakorlat Ismétlés: Megjegyzés: Az ismétlés egy része nem szerepel a dokumentumban, mivel lényegében a teljes 1.
Arany Dániel Matematikai Tanulóverseny 2016/2017-es tanév Kezdők III. kategória I. forduló
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 016/017-es tanév Kezdők I II. kategória II. forduló Kezdők III. kategória I. forduló Megoldások és javítási útmutató 1. Egy kört
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 016/017-es tanév Kezdők I II. kategória II. forduló Kezdők III. kategória I. forduló Megoldások és javítási útmutató 1. Egy kört
RE 1. Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Valasek Gábor valasek@inf.elte.hu
 Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata.
 1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata. HLMZOK halmaz axiomatikus fogalom, nincs definíciója. benne van valami a halmazban szintén axiomatikus fogalom,
1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata. HLMZOK halmaz axiomatikus fogalom, nincs definíciója. benne van valami a halmazban szintén axiomatikus fogalom,
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
1. Mátrixösszeadás és skalárral szorzás
 1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
3. Lineáris differenciálegyenletek
 3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
Műveletek egész számokkal
 Mit tudunk az egész számokról? 1. Döntsd el, hogy igazak-e a következő állítások az A halmaz elemeire! a) Az A halmaz elemei között 3 pozitív szám van. b) A legkisebb szám abszolút értéke a legnagyobb.
Mit tudunk az egész számokról? 1. Döntsd el, hogy igazak-e a következő állítások az A halmaz elemeire! a) Az A halmaz elemei között 3 pozitív szám van. b) A legkisebb szám abszolút értéke a legnagyobb.
Polinomok, Lagrange interpoláció
 Közelítő és szimbolikus számítások 8. gyakorlat Polinomok, Lagrange interpoláció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Polinomok
Közelítő és szimbolikus számítások 8. gyakorlat Polinomok, Lagrange interpoláció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Polinomok
Algoritmuselmélet 12. előadás
 Algoritmuselmélet 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Április 9. ALGORITMUSELMÉLET 12. ELŐADÁS 1 Turing-gépek
Algoritmuselmélet 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Április 9. ALGORITMUSELMÉLET 12. ELŐADÁS 1 Turing-gépek
FFT. Második nekifutás. Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék október 2.
 TARTALOMJEGYZÉK Polinomok konvolúviója A DFT és a maradékos osztás Gyűrűk támogatás nélkül Második nekifutás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. október 2. TARTALOMJEGYZÉK Polinomok
TARTALOMJEGYZÉK Polinomok konvolúviója A DFT és a maradékos osztás Gyűrűk támogatás nélkül Második nekifutás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. október 2. TARTALOMJEGYZÉK Polinomok
Determinánsok. A determináns fogalma olyan algebrai segédeszköz, amellyel. szolgáltat az előbbi kérdésekre, bár ez nem mindig hatékony.
 Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Klasszikus algebra előadás. Waldhauser Tamás április 28.
 Klasszikus algebra előadás Waldhauser Tamás 2014. április 28. 5. Számelmélet integritástartományokban Oszthatóság Mostantól R mindig tetszőleges integritástartományt jelöl. 5.1. Definíció. Azt mondjuk,
Klasszikus algebra előadás Waldhauser Tamás 2014. április 28. 5. Számelmélet integritástartományokban Oszthatóság Mostantól R mindig tetszőleges integritástartományt jelöl. 5.1. Definíció. Azt mondjuk,
1. A polinom fogalma. Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1. = x egyenletet.
 1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
Az informatika kulcsfogalmai
 Az informatika kulcsfogalmai Kulcsfogalmak Melyek azok a fogalmak, amelyek nagyon sok más fogalommal kapcsolatba hozhatók? Melyek azok a fogalmak, amelyek más-más környezetben újra és újra megjelennek?
Az informatika kulcsfogalmai Kulcsfogalmak Melyek azok a fogalmak, amelyek nagyon sok más fogalommal kapcsolatba hozhatók? Melyek azok a fogalmak, amelyek más-más környezetben újra és újra megjelennek?
Minden egész szám osztója önmagának, azaz a a minden egész a-ra.
 1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 7. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 7. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Makay Géza, makayg@math.u-szeged.hu, SZTE, Bolyai Intézet
 Makay Géza, makayg@math.u-szeged.hu, SZTE, Bolyai Intézet A SUDOKU szabályai, története A Sudoku egy cellából álló rács. A rács kilenc kisebb, -as blokkra oszlik, amelyben elszórva néhány -től -ig terjedő
Makay Géza, makayg@math.u-szeged.hu, SZTE, Bolyai Intézet A SUDOKU szabályai, története A Sudoku egy cellából álló rács. A rács kilenc kisebb, -as blokkra oszlik, amelyben elszórva néhány -től -ig terjedő
DISZKRÉT MATEMATIKA: STRUKTÚRÁK Előadáson mutatott példa: Bércesné Novák Ágnes
 1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
Adatbázisok elmélete 12. előadás
 Adatbázisok elmélete 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu http://www.cs.bme.hu/ kiskat 2005 ADATBÁZISOK ELMÉLETE
Adatbázisok elmélete 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu http://www.cs.bme.hu/ kiskat 2005 ADATBÁZISOK ELMÉLETE
Automaták és formális nyelvek
 Automaták és formális nyelvek Bevezetés a számítástudomány alapjaiba 1. Formális nyelvek 2006.11.13. 1 Automaták és formális nyelvek - bevezetés Automaták elmélete: információs gépek általános absztrakt
Automaták és formális nyelvek Bevezetés a számítástudomány alapjaiba 1. Formális nyelvek 2006.11.13. 1 Automaták és formális nyelvek - bevezetés Automaták elmélete: információs gépek általános absztrakt
Informatikai tehetséggondozás:
 Ég és Föld vonzásában a természet titkai Informatikai tehetséggondozás: isszalépéses kiválogatás TÁMOP-4.2.3.-12/1/KON isszalépéses kiválogatás 1. Az összes lehetséges sorrend Sokszor előfordul feladatként,
Ég és Föld vonzásában a természet titkai Informatikai tehetséggondozás: isszalépéses kiválogatás TÁMOP-4.2.3.-12/1/KON isszalépéses kiválogatás 1. Az összes lehetséges sorrend Sokszor előfordul feladatként,
Fibonacci számok. Dinamikus programozással
 Fibonacci számok Fibonacci 1202-ben vetette fel a kérdést: hány nyúlpár születik n év múlva, ha feltételezzük, hogy az első hónapban csak egyetlen újszülött nyúl-pár van; minden nyúlpár, amikor szaporodik
Fibonacci számok Fibonacci 1202-ben vetette fel a kérdést: hány nyúlpár születik n év múlva, ha feltételezzük, hogy az első hónapban csak egyetlen újszülött nyúl-pár van; minden nyúlpár, amikor szaporodik
összeadjuk 0-t kapunk. Képletben:
 814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
A sorozat fogalma. függvényeket sorozatoknak nevezzük. Amennyiben az értékkészlet. az értékkészlet a komplex számok halmaza, akkor komplex
 A sorozat fogalma Definíció. A természetes számok N halmazán értelmezett függvényeket sorozatoknak nevezzük. Amennyiben az értékkészlet a valós számok halmaza, valós számsorozatról beszélünk, mígha az
A sorozat fogalma Definíció. A természetes számok N halmazán értelmezett függvényeket sorozatoknak nevezzük. Amennyiben az értékkészlet a valós számok halmaza, valós számsorozatról beszélünk, mígha az
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Analízis I. Vizsgatételsor
 Analízis I. Vizsgatételsor Programtervező Informatikus szak 2008-2009. 2. félév Készítette: Szabó Zoltán SZZNACI.ELTE zotyo@bolyaimk.hu v.0.6 RC 004 Forrás: Oláh Gábor: ANALÍZIS I.-II. VIZSGATÉTELSOR 2006-2007-/2
Analízis I. Vizsgatételsor Programtervező Informatikus szak 2008-2009. 2. félév Készítette: Szabó Zoltán SZZNACI.ELTE zotyo@bolyaimk.hu v.0.6 RC 004 Forrás: Oláh Gábor: ANALÍZIS I.-II. VIZSGATÉTELSOR 2006-2007-/2
2005_01/1 Leírtunk egymás mellé hét racionális számot úgy, hogy a két szélső kivételével mindegyik eggyel nagyobb a két szomszédja szorzatánál.
 Számolásos feladatok, műveletek 2004_1/1 Töltsd ki az alábbi bűvös négyzet hiányzó mezőit úgy, hogy a négyzetben szereplő minden szám különböző legyen, és minden sorban, oszlopban és a két átlóban is ugyanannyi
Számolásos feladatok, műveletek 2004_1/1 Töltsd ki az alábbi bűvös négyzet hiányzó mezőit úgy, hogy a négyzetben szereplő minden szám különböző legyen, és minden sorban, oszlopban és a két átlóban is ugyanannyi
2014. november 5-7. Dr. Vincze Szilvia
 24. november 5-7. Dr. Vincze Szilvia A differenciálszámítás az emberiség egyik legnagyobb találmánya és ez az állítás nem egy matek-szakbarbár fellengzős kijelentése. A differenciálszámítás segítségével
24. november 5-7. Dr. Vincze Szilvia A differenciálszámítás az emberiség egyik legnagyobb találmánya és ez az állítás nem egy matek-szakbarbár fellengzős kijelentése. A differenciálszámítás segítségével
Halmazelmélet. 1. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Halmazelmélet p. 1/1
 Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Typotex Kiadó. Bevezetés
 Bevezetés A bennünket körülvevő világ leírásához ősidők óta számokat is alkalmazunk. Tekintsük át a számfogalom kiépülésének logikai-történeti folyamatát, amely minden valószínűség szerint a legkorábban
Bevezetés A bennünket körülvevő világ leírásához ősidők óta számokat is alkalmazunk. Tekintsük át a számfogalom kiépülésének logikai-történeti folyamatát, amely minden valószínűség szerint a legkorábban
Érdemes egy n*n-es táblázatban (sorok-lányok, oszlopok-fiúk) ábrázolni a két színnel, mely éleket húztuk be (pirossal, kékkel)
 Kombi/2 Egy bizonyos bulin n lány és n fiú vesz részt. Minden fiú pontosan a darab lányt és minden lány pontosan b darab fiút kedvel. Milyen (a,b) számpárok esetén létezik biztosan olyan fiúlány pár, akik
Kombi/2 Egy bizonyos bulin n lány és n fiú vesz részt. Minden fiú pontosan a darab lányt és minden lány pontosan b darab fiút kedvel. Milyen (a,b) számpárok esetén létezik biztosan olyan fiúlány pár, akik
1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy b = ax. Ennek jelölése a b.
 1. Oszthatóság, legnagyobb közös osztó Ebben a jegyzetben minden változó egész számot jelöl. 1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy
1. Oszthatóság, legnagyobb közös osztó Ebben a jegyzetben minden változó egész számot jelöl. 1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy
Mátrixok február Feladat: Legyen A = ( ( B =
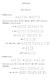 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Diszkrét matematika 1.
 Diszkrét matematika 1. 2017. ősz 1. Diszkrét matematika 1. 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra Tanszék
Diszkrét matematika 1. 2017. ősz 1. Diszkrét matematika 1. 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra Tanszék
Függvények december 6. Határozza meg a következő határértékeket! 1. Feladat: x 0 7x 15 x ) = lim. Megoldás: lim. 2. Feladat: lim.
 Függvények 05. december 6. Határozza meg a következő határértékeket!. Feladat: ( + 7 5 ) ( + 7 5 ) ( + 0 ). Feladat: ( + 7 5 ) ( + 7 5 ) ( + 0) 3. Feladat: ( + 0 7 5 ) 4. Feladat: ( + 0 7 5 ) ( + 7 0 5
Függvények 05. december 6. Határozza meg a következő határértékeket!. Feladat: ( + 7 5 ) ( + 7 5 ) ( + 0 ). Feladat: ( + 7 5 ) ( + 7 5 ) ( + 0) 3. Feladat: ( + 0 7 5 ) 4. Feladat: ( + 0 7 5 ) ( + 7 0 5
Számelmélet Megoldások
 Számelmélet Megoldások 1) Egy számtani sorozat második tagja 17, harmadik tagja 1. a) Mekkora az első 150 tag összege? (5 pont) Kiszámoltuk ebben a sorozatban az első 111 tag összegét: 5 863. b) Igaz-e,
Számelmélet Megoldások 1) Egy számtani sorozat második tagja 17, harmadik tagja 1. a) Mekkora az első 150 tag összege? (5 pont) Kiszámoltuk ebben a sorozatban az első 111 tag összegét: 5 863. b) Igaz-e,
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé.
 HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
Gráfelmélet. I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma
 Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
Konvexitás, elaszticitás
 DIFFERENCIÁLSZÁMÍTÁS ALKALMAZÁSAI Konveitás, elaszticitás Tanulási cél A másodrendű deriváltat vizsgálva milyen következtetéseket vonhatunk le a üggvény konveitására vonatkozóan. Elaszticitás ogalmának
DIFFERENCIÁLSZÁMÍTÁS ALKALMAZÁSAI Konveitás, elaszticitás Tanulási cél A másodrendű deriváltat vizsgálva milyen következtetéseket vonhatunk le a üggvény konveitására vonatkozóan. Elaszticitás ogalmának
1. ábra ábra
 A kifejtési tétel A kifejtési tétel kimondásához először meg kell ismerkedni az előjeles aldetermináns fogalmával. Ha az n n-es A mátrix i-edik sorának és j-edik oszlopának kereszteződésében az elem áll,
A kifejtési tétel A kifejtési tétel kimondásához először meg kell ismerkedni az előjeles aldetermináns fogalmával. Ha az n n-es A mátrix i-edik sorának és j-edik oszlopának kereszteződésében az elem áll,
Irodalom. (a) A T, B T, (b) A + B, C + D, D C, (c) 3A, (d) AD, DA, B T A, 1 2 B = 1 C = A = 1 0 D = (a) 1 1 3, B T = = ( ) ; A T = 1 0
 Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Taylor-polinomok. 1. Alapfeladatok. 2015. április 11. 1. Feladat: Írjuk fel az f(x) = e 2x függvény másodfokú Maclaurinpolinomját!
 Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
1. A Horner-elrendezés
 1. A Horner-elrendezés A polinomok műveleti tulajdonságai Polinomokkal a szokásos módon számolhatunk: Tétel (K2.1.6, HF ellenőrizni) Tetszőleges f,g,h polinomokra érvényesek az alábbiak. (1) (f +g)+h =
1. A Horner-elrendezés A polinomok műveleti tulajdonságai Polinomokkal a szokásos módon számolhatunk: Tétel (K2.1.6, HF ellenőrizni) Tetszőleges f,g,h polinomokra érvényesek az alábbiak. (1) (f +g)+h =
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 3 III. MEGFELELTETÉSEk, RELÁCIÓk 1. BEVEZETÉS Emlékeztetünk arra, hogy az rendezett párok halmazát az és halmazok Descartes-féle szorzatának nevezzük. Más szóval az és halmazok
KOVÁCS BÉLA, MATEmATIkA I. 3 III. MEGFELELTETÉSEk, RELÁCIÓk 1. BEVEZETÉS Emlékeztetünk arra, hogy az rendezett párok halmazát az és halmazok Descartes-féle szorzatának nevezzük. Más szóval az és halmazok
karakterisztikus egyenlet Ortogonális mátrixok. Kvadratikus alakok főtengelytranszformációja
 Mátrixok hasonlósága, karakterisztikus mátrix, karakterisztikus egyenlet Ortogonális mátrixok. Kvadratikus alakok főtengelytranszformációja 1.Mátrixok hasonlósága, karakterisztikus mátrix, karakterisztikus
Mátrixok hasonlósága, karakterisztikus mátrix, karakterisztikus egyenlet Ortogonális mátrixok. Kvadratikus alakok főtengelytranszformációja 1.Mátrixok hasonlósága, karakterisztikus mátrix, karakterisztikus
JELENTKEZÉSI LAP. Név: Osztály: E-mail cím (továbbjutásról itt is értesítünk): Iskola: Felkészítő tanár:
 JELENTKEZÉSI LAP Név: Osztály: E-mail cím (továbbjutásról itt is értesítünk): Iskola: Felkészítő tanár: Második fordulóba jutás esetén Windows 7 operációs rendszert, és Office 2007 programcsomagot fogsz
JELENTKEZÉSI LAP Név: Osztály: E-mail cím (továbbjutásról itt is értesítünk): Iskola: Felkészítő tanár: Második fordulóba jutás esetén Windows 7 operációs rendszert, és Office 2007 programcsomagot fogsz
0,424 0,576. f) P (X 2 = 3) g) P (X 3 = 1) h) P (X 4 = 1 vagy 2 X 2 = 2) i) P (X 7 = 3, X 4 = 1, X 2 = 2 X 0 = 2) j) P (X 7 = 3, X 4 = 1, X 2 = 2)
 Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Egész számok. pozitív egész számok: 1; 2; 3; 4;... negatív egész számok: 1; 2; 3; 4;...
 Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 függvények RE 1 Relációk Függvények függvények RE 2 Definíció Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor
függvények RE 1 Relációk Függvények függvények RE 2 Definíció Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor
Gauss-eliminációval, Cholesky felbontás, QR felbontás
 Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
(Diszkrét idejű Markov-láncok állapotainak
 (Diszkrét idejű Markov-láncok állapotainak osztályozása) March 21, 2019 Markov-láncok A Markov-láncok anaĺızise főként a folyamat lehetséges realizációi valószínűségeinek kiszámolásával foglalkozik. Ezekben
(Diszkrét idejű Markov-láncok állapotainak osztályozása) March 21, 2019 Markov-láncok A Markov-láncok anaĺızise főként a folyamat lehetséges realizációi valószínűségeinek kiszámolásával foglalkozik. Ezekben
Waldhauser Tamás december 1.
 Algebra és számelmélet előadás Waldhauser Tamás 2016. december 1. Tizedik házi feladat az előadásra Hányféleképpen lehet kiszínezni az X-pentominót n színnel, ha a forgatással vagy tükrözéssel egymásba
Algebra és számelmélet előadás Waldhauser Tamás 2016. december 1. Tizedik házi feladat az előadásra Hányféleképpen lehet kiszínezni az X-pentominót n színnel, ha a forgatással vagy tükrözéssel egymásba
Megjegyzés: A programnak tartalmaznia kell legalább egy felhasználói alprogramot. Példa:
 1. Tétel Az állomány két sort tartalmaz. Az első sorában egy nem nulla természetes szám van, n-el jelöljük (5
1. Tétel Az állomány két sort tartalmaz. Az első sorában egy nem nulla természetes szám van, n-el jelöljük (5
Lineáris algebra (10A103)
 Lineáris algebra (10A103) Kátai-Urbán Kamilla (1. előadás) Mátrixok 2019. február 6. 1 / 35 Bevezetés Előadás Tudnivalók (I.) Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Az előadáson készített
Lineáris algebra (10A103) Kátai-Urbán Kamilla (1. előadás) Mátrixok 2019. február 6. 1 / 35 Bevezetés Előadás Tudnivalók (I.) Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Az előadáson készített
ARCHIMEDES MATEMATIKA VERSENY
 Koszinusztétel Tétel: Bármely háromszögben az egyik oldal négyzetét megkapjuk, ha a másik két oldal négyzetének összegéből kivonjuk e két oldal és az általuk közbezárt szög koszinuszának kétszeres szorzatát.
Koszinusztétel Tétel: Bármely háromszögben az egyik oldal négyzetét megkapjuk, ha a másik két oldal négyzetének összegéből kivonjuk e két oldal és az általuk közbezárt szög koszinuszának kétszeres szorzatát.
5. előadás. Programozás-elmélet. Programozás-elmélet 5. előadás
 Elemi programok Definíció Az S A A program elemi, ha a A : S(a) { a, a, a, a,..., a, b b a}. A definíció alapján könnyen látható, hogy egy elemi program tényleg program. Speciális elemi programok a kövekezők:
Elemi programok Definíció Az S A A program elemi, ha a A : S(a) { a, a, a, a,..., a, b b a}. A definíció alapján könnyen látható, hogy egy elemi program tényleg program. Speciális elemi programok a kövekezők:
30. ERŐSEN ÜSSZEFÜGGŐ KOMPONENSEK
 30. ERŐSEN ÜSSZEFÜGGŐ KOMPONENSEK A gráfos alkalmazások között is találkozunk olyan problémákkal, amelyeket megoldását a részekre bontott gráfon határozzuk meg, majd ezeket alkalmas módon teljes megoldássá
30. ERŐSEN ÜSSZEFÜGGŐ KOMPONENSEK A gráfos alkalmazások között is találkozunk olyan problémákkal, amelyeket megoldását a részekre bontott gráfon határozzuk meg, majd ezeket alkalmas módon teljes megoldássá
HHF0CX. k darab halmaz sorbarendezésének a lehetősége k! Így adódik az alábbi képlet:
 Gábor Miklós HHF0CX 5.7-16. Vegyük úgy, hogy a feleségek akkor vannak a helyükön, ha a saját férjeikkel táncolnak. Ekkor már látszik, hogy azon esetek száma, amikor senki sem táncol a saját férjével, megegyezik
Gábor Miklós HHF0CX 5.7-16. Vegyük úgy, hogy a feleségek akkor vannak a helyükön, ha a saját férjeikkel táncolnak. Ekkor már látszik, hogy azon esetek száma, amikor senki sem táncol a saját férjével, megegyezik
