Egyirányban láncolt lista
|
|
|
- Márta Kiss
- 8 évvel ezelőtt
- Látták:
Átírás
1 Egyirányban láncolt lista A tárhely (listaelem) az adatelem értékén kívül egy mutatót tartalmaz, amely a következő listaelem címét tartalmazza. A láncolt lista első elemének címét egy, a láncszerkezeten kívüli mutató, a fejmutató tárolja. A fejmutató nem tartalmaz egyéb adatot a mutatón kívül, így nem része az adatszerkezetnek, csak a hozzáférést biztosítja ahhoz. A láncolt lista végét egy speciális érték, a NIL jelzi. Amennyiben a fejmutató értéke NIL, akkor a lista üres. Ha a fej értéke nem NIL, kötelezően mutat egy tárhelyre, amely tartalmazza a lista első elemét. 1
2 Egyirányban láncolt lista Kedvező a beszúrásos rendezés számára. Előnyös, hogy a módosítási műveletek nem igényelnek adatmozgatást, valamint dinamikusságából következően nem kell előre meghatározni a tárhelyek számát. Nehéz benne keresni. Csak a teljes, és rendezett listában a lineáris keresés valósítható meg. 2
3 Egyirányban láncolt lista: Létrehozás 1. A fejmutató létrehozása, és 2. feltöltése a NIL értékkel. Ezzel létrejött egy üres egyirányban láncolt lista. 3
4 Egyirányban láncolt lista: Bővítés (az elején) 1. Tárhelyet foglalunk az új elem számára 2. A tárhely (új listaelem) adat részébe beírjuk a tárolandó elem értékét. 3. A tárhely mutató részébe átmásoljuk a fejmutató értékét. (Most egy ideig egyszerre két mutató is kijelöli a lista eddigi első elemét.) 4. Fejmutatóba beírjuk az új elem tárhelyének címét. A 3. és 4. lépés nem felcserélhető! (Az algoritmusok végrehajtása szekvenciális.) Van még: Bővítés a lista végén Bővítés az aktuális elem előtt vagy után 4
5 adat1 adat2 adatn Fej TMP Uj adat? Uj adat 1 & 2 TMP 3 adat1 adat2 adatn Fej 4 Uj adat TMP 5
6 Egyirányban láncolt lista: Törlés Bármelyik elem törölhető, de előre meg kell határozni, melyik ez az elem. Ha nem úgy van megfogalmazva a feladat, hogy töröld az első elemet, akkor a törlés művelete minden esetben a törlendő elem keresésével kezdődik. Első elem tölése: 1. Ha a lista üres (fejmutató==nil), az algoritmus véget ért. 2. A fejmutató új értéke legyen, a fej által mutatott elem mutató részében tárolt érték (a következő elem címe). Ezután a lista egy elemmel kevesebbet tartalmaz. 6
7 Egyirányban láncolt lista: Csere Egyirányban láncolt listában a csere minden esetben kereséssel kezdődik. Ha a keresés sikeres, a megtalált értéket a csrélendő új értékkel felülírjuk. 7
8 Egyirányban láncolt lista: Rendezés Egyirányban láncolt listában lehet ugyan rendezni, de nem szokás. Helyette, ha fontos a lista rendezettsége (pl. mert szeretnénk teljes keresés helyett lineáris keresést alkalmazni), akkor a bővítés műveletét módosítjuk olyan módon, hogy a rendezett egyirányban láncolt lista a bővítés közben megőrizze rendezettségét. (Beszúró rendezés képezi az alapját a rendezett lista bővítésének.) 8
9 Egyirányban láncolt lista: Feldolgozás A feldogozásnak minden esetben a keresés vagy a bejárás az alapja. 9
10 Ciklikus lista Az egyirányban láncolt listának a feldolgozást segítő módosítása. Abban különbözik az egyirányban láncolt listától, hogy egyetlen listaelem sem tartalmaz a mutató részében NIL-t. Az utolsó elem mutató része a lista első elemére mutat. Ennek a listának is van fejmutatója, ami az első elemhez való hozzáférést segíti, illetve lehetővé teszi az utolsó elem felismerését, hiszen annak mutató része ugyanazt az értéket tartalmazza, mint a fejmutató. (Mindketten az első elemre mutatnak.) 10
11 Egyirányban láncolt lista: adat1 adat2 adatn Fej Ciklikus lista: Fej adat1 adat2 adatn 11
12 Kétirányban láncolt lista Az adatelemek itt is adat részből és muató részből állnak. DE a mutató rész két mutatót tartalmaz: Az egyik mutatja -mint eddig- a rákövetkező adatelem tárhelyét, a másik pedig a megelőző adatelem tárhelyét. Ebben a szerkezetben az adatelemekhez való hozzáférést a fejmutatón kívül még egy vége mutató is segíti. Ez utóbbi az utolsó adatelem tárhelyének címét tartalmazza. (Akár úgy is tekinthetünk rájuk, mint két egyirányban láncolt lista fejmutatóira.) Ebben a szerkezetben egyszerűbb a fizikai törlés, mivel közvetlenül meg tudjuk fogni a törlendő elem 12 megelőzőjét és rákövetkezőjét.
13 Egy irányban láncolt lista: adat1 adat2 adatn Fej Két irányban láncolt lista: Fej adat1 adat2 adatn Vége 13
14 Multilista (1) A listaelemek adatrésze összetett, több atomi értéket tartalmaz Mindegyik atomi értékre föl lehet építeni 1-1 láncolt listát Minden tárhely (legalább) annyi muatót tartalmaz, ahány listába szerveztük az elemeket. Annyi fejmutatóra van szükség, ahány listánk van. Minden elem benne van az összes listában. 14
15 Multilista (1): Betű X 2 Szám G 7 K 9 15
16 Multilista (2) Részláncokat hozunk létre. Azok az elemek kerülnek egy részláncba, melyeknek adatrésze megegyezik. Pontosan annyi részlánc van, ahány különböző érték fordul elő az adatelemek között. A részláncok nem fedik át egymást, minden atomi adatelem csak egyetlen részláncban szerepel. Annyi fejmutató létezik, ahány részlánc. 16
17 Multilista (2): Abc Def Qwe 4.érték 5.érték Abc Def Def Def Abc 5.érték Qwe Abc Qwe 17
18 Multilista (3) Itt a tárhelyekbe is be lehet építeni listafejeket. Egy listaelem adatrésze vagy tényleges atomi értéket tárol, vagy egy másik láncszerkezet első elemének a címét. Hogy a kettő közül melyiket, azt egy egyetlen biten tárolt információval dönthetjük el. Pl. 0 == > listafej 1 == > tényleges atomi érték 18
19 Multilista (3): Fej Adat3 1 Adat1 0 1 Adat4 1 Adat5 1 Adat2 1 Adat6 19
20 Folytonos és szétszórt ábrázolás Az egyes absztrakt adatszerkezetek mind folytonos, mind szétszórt módon ábrázolhatóak. DE: a leképezés annál egyszerűbb, minél jobban illeszkedik egymáshoz az absztrakt adatszerkezet és a tárolási szerkezet. Az asszociatív adatszerkezetek nagyon jól tárolhatók folytonosan. A hierarchikus és hálós szerkezetek viszont elsősorban szétszórt módon kezelhetőek könnyen. A szekvenciális adatszerkezetek mindkét módon jól kezelhetőek. 20
21 Reprezentáció és Implementáció absztrakt adatszerkezet ->leképezés-> ábrázolás Absztrakt adatszerkezet reprezentációja: A tárolási mód Leképezés Absztrakt adatszerkezet implementációja: reprezentáció A műveleteket megvalósító algoritmusok Az algoritmusok megadhatóak: beszélt emberi nyelven mondatszerű leírással folyamatábrával pszeudonyelvvel (gyakorlatokon) Programozási nyelvven 21
22 Szabad helyek kezelése A memória véges. Az adatszerkezetek elemeit a memóriában tároljuk. == > A memóriával gazdálkodni kell. Ebben az egyik fontos elem, a felszabaduló tárhelyek újrahasznosítása. Két alapvető módszer Kézi (Manual memory management) NEW,. FREE,.. Hulladékgyűjtés (Garbage collection) NEW,. Mutató értékadások figyelése Már nem hivatkozott tárhelyek automatikus felismerése 22
23 Felszabadult helyek nyilvántartása, kezelése Szabad helyek nyilvántartása A szabad tárhelyeket a lefoglalt memória végére gyűjtjük össze. (Időigényes lehet.) Minden lefoglalt tárhelyhez hozzárendelünk egy bitet, amely jelzi a foglaltságot (1). (szabad 0) (Bonyolultabb a kezelés.) Szabad helyek láncolt listájának megvalósítása Mindezek kombinációi Új helyek kiosztása Az első szabad, megfelelő méretű A legjobban illeszkedő 23
24 Szabad helyek kezelése: Szétszórt ábrázolás Bitsorozatok (Itt a foglaltság mellett a tárhely címét is tárolni kell. Csak elvi lehetőség.) Szabad helyek láncolt listájának megvalósítása Egyirányban láncolt lista. (azonos méret) Ha nem == > első v. legjobban illeszkedő Valamely adatszerkezet bővít == > a lista elejéről adunk neki tárhelyet. Valamely adaszerkezet (fizikailag) töröl == > a lista elejére szúrjuk be a felszabaduló tárhelyet Szemét gyűjtögetés itt is automatikus, fizikai törlés esetén jellemzője a hivatkozás figyelés, azaz csak azt a tárhelyet gyűjti, melyre nincs élő hivatkozás 24
Adatszerkezetek 1. előadás
 Adatszerkezetek 1. előadás Irodalom: Lipschutz: Adatszerkezetek Morvay, Sebők: Számítógépes adatkezelés Cormen, Leiserson, Rives, Stein: Új algoritmusok http://it.inf.unideb.hu/~halasz http://it.inf.unideb.hu/adatszerk
Adatszerkezetek 1. előadás Irodalom: Lipschutz: Adatszerkezetek Morvay, Sebők: Számítógépes adatkezelés Cormen, Leiserson, Rives, Stein: Új algoritmusok http://it.inf.unideb.hu/~halasz http://it.inf.unideb.hu/adatszerk
10. előadás Speciális többágú fák
 10. előadás Adatszerkezetek és algoritmusok előadás 2018. április 17., és Debreceni Egyetem Informatikai Kar 10.1 A többágú fák kezelésére nincsenek általános elvek, implementációjuk elsősorban alkalmazásfüggő.
10. előadás Adatszerkezetek és algoritmusok előadás 2018. április 17., és Debreceni Egyetem Informatikai Kar 10.1 A többágú fák kezelésére nincsenek általános elvek, implementációjuk elsősorban alkalmazásfüggő.
A lista adatszerkezet A lista elemek egymásutániságát jelenti. Fajtái: statikus, dinamikus lista.
 Lista adatszerkezet A lista adatszerkezet jellemzői 1 Különböző problémák számítógépes megoldása során gyakran van szükség olyan adatszerkezetre, amely nagyszámú, azonos típusú elem tárolására alkalmas,
Lista adatszerkezet A lista adatszerkezet jellemzői 1 Különböző problémák számítógépes megoldása során gyakran van szükség olyan adatszerkezetre, amely nagyszámú, azonos típusú elem tárolására alkalmas,
Struktúra nélküli adatszerkezetek
 Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Láncolt listák. Egyszerű, rendezett és speciális láncolt listák. Programozás II. előadás. Szénási Sándor
 Láncolt listák Egyszerű, rendezett és speciális láncolt listák előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Láncolt
Láncolt listák Egyszerű, rendezett és speciális láncolt listák előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Láncolt
Láncolt Listák. Adat1 Adat2 Adat3 ø. Adat1 Adat2 ø Adat3
 Láncolt Listák Adatszerkezetek Adatszerkezet: Az adatelemek egy olyan véges halmaza, amelyben az adatelemek között szerkezeti összefüggések vannak Megvalósítások: - Tömb, Láncolt lista, Fa, Kupac, Gráf,
Láncolt Listák Adatszerkezetek Adatszerkezet: Az adatelemek egy olyan véges halmaza, amelyben az adatelemek között szerkezeti összefüggések vannak Megvalósítások: - Tömb, Láncolt lista, Fa, Kupac, Gráf,
Láncolt listák. PPT 2007/2008 tavasz.
 Láncolt listák szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Témakörök Láncolt listák elvi felépítése Egyirányú egyszerű láncolt lista Egyirányú rendezett láncolt lista Láncolt
Láncolt listák szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Témakörök Láncolt listák elvi felépítése Egyirányú egyszerű láncolt lista Egyirányú rendezett láncolt lista Láncolt
Láncolt listák Témakörök. Lista alapfogalmak
 Láncolt listák szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Lista alapfogalmai Egyirányú egyszerű láncolt lista Egyirányú rendezett láncolt lista Speciális láncolt listák Témakörök
Láncolt listák szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Lista alapfogalmai Egyirányú egyszerű láncolt lista Egyirányú rendezett láncolt lista Speciális láncolt listák Témakörök
Algoritmusok és adatszerkezetek gyakorlat 06 Adatszerkezetek
 Algoritmusok és adatszerkezetek gyakorlat 06 Adatszerkezetek Tömb Ugyanolyan típusú elemeket tárol A mérete előre definiált kell legyen és nem lehet megváltoztatni futás során Legyen n a tömb mérete. Ekkor:
Algoritmusok és adatszerkezetek gyakorlat 06 Adatszerkezetek Tömb Ugyanolyan típusú elemeket tárol A mérete előre definiált kell legyen és nem lehet megváltoztatni futás során Legyen n a tömb mérete. Ekkor:
Adatszerkezetek Adatszerkezet fogalma. Az értékhalmaz struktúrája
 Adatszerkezetek Összetett adattípus Meghatározói: A felvehető értékek halmaza Az értékhalmaz struktúrája Az ábrázolás módja Műveletei Adatszerkezet fogalma Direkt szorzat Minden eleme a T i halmazokból
Adatszerkezetek Összetett adattípus Meghatározói: A felvehető értékek halmaza Az értékhalmaz struktúrája Az ábrázolás módja Műveletei Adatszerkezet fogalma Direkt szorzat Minden eleme a T i halmazokból
end function Az A vektorban elõforduló legnagyobb és legkisebb értékek indexeinek különbségét.. (1.5 pont) Ha üres a vektor, akkor 0-t..
 A Név: l 2014.04.09 Neptun kód: Gyakorlat vezető: HG BP MN l 1. Adott egy (12 nem nulla értékû elemmel rendelkezõ) 6x7 méretû ritka mátrix hiányos 4+2 soros reprezentációja. SOR: 1 1 2 2 2 3 3 4 4 5 6
A Név: l 2014.04.09 Neptun kód: Gyakorlat vezető: HG BP MN l 1. Adott egy (12 nem nulla értékû elemmel rendelkezõ) 6x7 méretû ritka mátrix hiányos 4+2 soros reprezentációja. SOR: 1 1 2 2 2 3 3 4 4 5 6
9. előadás. A táblázat. A táblázatról általában, soros, önátrendező, rendezett és kulcstranszformációs táblázat
 . előadás ról általában, soros, önátrendező, rendezett és kulcstranszformációs Adatszerkezetek és algoritmusok előadás 0. április. ról általában,, és Debreceni Egyetem Informatikai Kar. Általános tudnivalók
. előadás ról általában, soros, önátrendező, rendezett és kulcstranszformációs Adatszerkezetek és algoritmusok előadás 0. április. ról általában,, és Debreceni Egyetem Informatikai Kar. Általános tudnivalók
A programozás alapjai előadás. [<struktúra változó azonosítók>] ; Dinamikus adatszerkezetek:
![A programozás alapjai előadás. [<struktúra változó azonosítók>] ; Dinamikus adatszerkezetek: A programozás alapjai előadás. [<struktúra változó azonosítók>] ; Dinamikus adatszerkezetek:](/thumbs/88/114858127.jpg) A programozás alapjai 1 Dinamikus adatszerkezetek:. előadás Híradástechnikai Tanszék Dinamikus adatszerkezetek: Adott építőelemekből, adott szabályok szerint felépített, de nem rögzített méretű adatszerkezetek.
A programozás alapjai 1 Dinamikus adatszerkezetek:. előadás Híradástechnikai Tanszék Dinamikus adatszerkezetek: Adott építőelemekből, adott szabályok szerint felépített, de nem rögzített méretű adatszerkezetek.
Programozás alapjai II. (7. ea) C++ Speciális adatszerkezetek. Tömbök. Kiegészítő anyag: speciális adatszerkezetek
 Programozás alapjai II. (7. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT M Ű E G Y E T E M 1 7 8 2 C++ programozási nyelv BME-IIT Sz.I. 2016.04.05. - 1
Programozás alapjai II. (7. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT M Ű E G Y E T E M 1 7 8 2 C++ programozási nyelv BME-IIT Sz.I. 2016.04.05. - 1
6. LISTÁK ábra. A lista absztrakt adatszerkezet (ADS)
 6. LISTÁK Az előző fejezetekben megismerkedtünk a láncolt ábrázolással. Láttuk a verem és a sor, valamint előre tekintve a keresőfa pointeres megvalósításának a lehetőségét és előnyeit. A láncolt ábrázolással
6. LISTÁK Az előző fejezetekben megismerkedtünk a láncolt ábrázolással. Láttuk a verem és a sor, valamint előre tekintve a keresőfa pointeres megvalósításának a lehetőségét és előnyeit. A láncolt ábrázolással
Programozás I. - 11. gyakorlat
 Programozás I. - 11. gyakorlat Struktúrák, gyakorlás Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 16, 2009 1 tar@dcs.vein.hu Tar
Programozás I. - 11. gyakorlat Struktúrák, gyakorlás Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 16, 2009 1 tar@dcs.vein.hu Tar
Programozás alapjai C nyelv 8. gyakorlat. Mutatók és címek (ism.) Indirekció (ism)
 Programozás alapjai C nyelv 8. gyakorlat Szeberényi Imre BME IIT Programozás alapjai I. (C nyelv, gyakorlat) BME-IIT Sz.I. 2005.11.07. -1- Mutatók és címek (ism.) Minden változó és függvény
Programozás alapjai C nyelv 8. gyakorlat Szeberényi Imre BME IIT Programozás alapjai I. (C nyelv, gyakorlat) BME-IIT Sz.I. 2005.11.07. -1- Mutatók és címek (ism.) Minden változó és függvény
Speciális adatszerkezetek. Programozás alapjai II. (8. ea) C++ Tömbök. Tömbök/2. N dimenziós tömb. Nagyméretű ritka tömbök
 Programozás alapjai II. (8. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT Speciális adatszerkezetek A helyes adatábrázolás választása, a helyes adatszerkezet
Programozás alapjai II. (8. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT Speciális adatszerkezetek A helyes adatábrázolás választása, a helyes adatszerkezet
Adatszerkezetek és algoritmusok
 Adatszerkezetek és algoritmusok Jegyzet dr. Juhász István előadása alapján Készítette Csordás Annamária és Mohai Gábor A valós világban rendszerekről beszélünk. A dolgok összetevői egymással kölcsönhatásban
Adatszerkezetek és algoritmusok Jegyzet dr. Juhász István előadása alapján Készítette Csordás Annamária és Mohai Gábor A valós világban rendszerekről beszélünk. A dolgok összetevői egymással kölcsönhatásban
1.előadás Tornai Kálmán
 1.előadás Tornai Kálmán tornai.kalman@itk.ppke.hu Általános tudnivalók Előadás: 2 óra (Labor)gyakorlat: 3 óra Előismeretek: Kötelező: Bevezetés a programozásba I-II. Algebra és diszkrét matematika I. II.
1.előadás Tornai Kálmán tornai.kalman@itk.ppke.hu Általános tudnivalók Előadás: 2 óra (Labor)gyakorlat: 3 óra Előismeretek: Kötelező: Bevezetés a programozásba I-II. Algebra és diszkrét matematika I. II.
5. SOR. Üres: S Sorba: S E S Sorból: S S E Első: S E
 5. SOR A sor adatszerkezet is ismerős a mindennapokból, például a várakozási sornak számos előfordulásával van dolgunk, akár emberekről akár tárgyakról (pl. munkadarabokról) legyen szó. A sor adattípus
5. SOR A sor adatszerkezet is ismerős a mindennapokból, például a várakozási sornak számos előfordulásával van dolgunk, akár emberekről akár tárgyakról (pl. munkadarabokról) legyen szó. A sor adattípus
Programozás alapjai II. (7. ea) C++
 Programozás alapjai II. (7. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT M Ű E G Y E T E M 1 7 8 2 C++ programozási nyelv BME-IIT Sz.I. 2016.04.05. - 1
Programozás alapjai II. (7. ea) C++ Kiegészítő anyag: speciális adatszerkezetek Szeberényi Imre BME IIT M Ű E G Y E T E M 1 7 8 2 C++ programozási nyelv BME-IIT Sz.I. 2016.04.05. - 1
Kulcs transzformációs táblázat
 Kulcs transzformációs táblázat Ennek a táblázatnak az ábrázolása folytonos. Soros táblázat esetén egy elem helyét a beszúrás időpontja, önátrendező táblázatnál a feldolgozás gyakorisága, rendezett táblázatnál
Kulcs transzformációs táblázat Ennek a táblázatnak az ábrázolása folytonos. Soros táblázat esetén egy elem helyét a beszúrás időpontja, önátrendező táblázatnál a feldolgozás gyakorisága, rendezett táblázatnál
Adatszerkezetek 1. Dr. Iványi Péter
 Adatszerkezetek 1. Dr. Iványi Péter 1 Adat Adat minden, amit a számítógépünkben tárolunk és a külvilágból jön Az adatnak két fontos tulajdonsága van: Értéke Típusa 2 Adat típusa Az adatot kódoltan tároljuk
Adatszerkezetek 1. Dr. Iványi Péter 1 Adat Adat minden, amit a számítógépünkben tárolunk és a külvilágból jön Az adatnak két fontos tulajdonsága van: Értéke Típusa 2 Adat típusa Az adatot kódoltan tároljuk
22. GRÁFOK ÁBRÁZOLÁSA
 22. GRÁFOK ÁBRÁZOLÁSA A megoldandó feladatok, problémák modellezése során sokszor gráfokat alkalmazunk. A gráf fogalmát a matematikából ismertnek vehetjük. A modellezés során a gráfok több változata is
22. GRÁFOK ÁBRÁZOLÁSA A megoldandó feladatok, problémák modellezése során sokszor gráfokat alkalmazunk. A gráf fogalmát a matematikából ismertnek vehetjük. A modellezés során a gráfok több változata is
A számítástudomány alapjai. Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem
 A számítástudomány alapjai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Bináris keresőfa, kupac Katona Gyula Y. (BME SZIT) A számítástudomány
A számítástudomány alapjai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Bináris keresőfa, kupac Katona Gyula Y. (BME SZIT) A számítástudomány
Algoritmuselmélet 2. előadás
 Algoritmuselmélet 2. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Február 12. ALGORITMUSELMÉLET 2. ELŐADÁS 1 Buborék-rendezés
Algoritmuselmélet 2. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Február 12. ALGORITMUSELMÉLET 2. ELŐADÁS 1 Buborék-rendezés
Táblázatok fontosabb műveletei 1
 Táblázatok fontosabb műveletei 1 - - Soros táblázat procedure BESZÚR1(TÁBLA, újelem) - - beszúrás soros táblázatba - - a táblázatot egy rekordokat tartalmazó dinamikus vektorral reprezentáljuk - - a rekordok
Táblázatok fontosabb műveletei 1 - - Soros táblázat procedure BESZÚR1(TÁBLA, újelem) - - beszúrás soros táblázatba - - a táblázatot egy rekordokat tartalmazó dinamikus vektorral reprezentáljuk - - a rekordok
Algoritmusok és adatszerkezetek I. 1. előadás
 Algoritmusok és adatszerkezetek I 1 előadás Típusok osztályozása Összetettség (strukturáltság) szempontjából: elemi (vagy skalár, vagy strukturálatlan) összetett (más szóval strukturált) Strukturálási
Algoritmusok és adatszerkezetek I 1 előadás Típusok osztályozása Összetettség (strukturáltság) szempontjából: elemi (vagy skalár, vagy strukturálatlan) összetett (más szóval strukturált) Strukturálási
Adatbáziskezelés. Indexek, normalizálás NZS 1
 Adatbáziskezelés Indexek, normalizálás NZS 1 Fáljszervezés módjai Soros elérés: a rekordok a fájlban tetszőleges sorrendben, például a felvitel sorrendjében helyezkednek el. A rekord azonosítója vagyis
Adatbáziskezelés Indexek, normalizálás NZS 1 Fáljszervezés módjai Soros elérés: a rekordok a fájlban tetszőleges sorrendben, például a felvitel sorrendjében helyezkednek el. A rekord azonosítója vagyis
Mutatók és címek (ism.) Programozás alapjai C nyelv 8. gyakorlat. Indirekció (ism) Néhány dolog érthetőbb (ism.) Változók a memóriában
 Programozás alapjai C nyelv 8. gyakorlat Szeberényi mre BME T Programozás alapjai. (C nyelv, gyakorlat) BME-T Sz.. 2005.11.07. -1- Mutatók és címek (ism.) Minden változó és függvény
Programozás alapjai C nyelv 8. gyakorlat Szeberényi mre BME T Programozás alapjai. (C nyelv, gyakorlat) BME-T Sz.. 2005.11.07. -1- Mutatók és címek (ism.) Minden változó és függvény
2. Milyen értéket határoz meg az alábbi algoritmus, ha A egy vektor?. (2 pont)
 A Név: l 2017.04.06 Neptun kód: Gyakorlat vezet : HG BP l 1. Az A vektor tartalmát az alábbi KUPACOL eljárással rendezzük át maximum kupaccá. A={28, 87, 96, 65, 55, 32, 51, 69} Mi lesz az értéke az A vektor
A Név: l 2017.04.06 Neptun kód: Gyakorlat vezet : HG BP l 1. Az A vektor tartalmát az alábbi KUPACOL eljárással rendezzük át maximum kupaccá. A={28, 87, 96, 65, 55, 32, 51, 69} Mi lesz az értéke az A vektor
Miről lesz ma szó? A PROGAMOZÁS ALAPJAI 1. Dinamikus adatszerkezetek. Dinamikus adatszerkezetek. Önhivatkozó struktúrák. Önhivatkozó struktúrák
 2012. március 27. A PROGAMOZÁS ALAPJAI 1 Vitéz András egyetemi adjunktus BME Híradástechnikai Tanszék vitez@hit.bme.hu Miről lesz ma szó? Dinamikus adatszerkezetek Önhivatkozó struktúra keresés, beszúrás,
2012. március 27. A PROGAMOZÁS ALAPJAI 1 Vitéz András egyetemi adjunktus BME Híradástechnikai Tanszék vitez@hit.bme.hu Miről lesz ma szó? Dinamikus adatszerkezetek Önhivatkozó struktúra keresés, beszúrás,
Hierarchikus adatszerkezetek
 5. előadás Hierarchikus adatszerkezetek A hierarchikus adatszerkezet olyan < A, R > rendezett pár, amelynél van egy kitüntetett r A gyökérelem úgy, hogy: 1. r nem lehet végpont, azaz a A esetén R(a,r)
5. előadás Hierarchikus adatszerkezetek A hierarchikus adatszerkezet olyan < A, R > rendezett pár, amelynél van egy kitüntetett r A gyökérelem úgy, hogy: 1. r nem lehet végpont, azaz a A esetén R(a,r)
Buborékrendezés: Hanoi Tornyai: Asszimptótikus fv.ek: Láncolt ábrázolás: For ciklussal:
 Buborékrendezés: For ciklussal: Hanoi Tornyai: Asszimptótikus fv.ek: Láncolt ábr.: ha p egy mutató típusú változó akkor p^ az általa mutatott adatelem, p^.adat;p^.mut. A semmibe mutató ponter a NIL.Szabad
Buborékrendezés: For ciklussal: Hanoi Tornyai: Asszimptótikus fv.ek: Láncolt ábr.: ha p egy mutató típusú változó akkor p^ az általa mutatott adatelem, p^.adat;p^.mut. A semmibe mutató ponter a NIL.Szabad
Algoritmusok és adatszerkezetek I. 4. előadás
 Algoritmusok és adatszerkezetek I. 4. előadás A lista olyan sorozat, amelyben műveleteket egy kiválasztott, az ún. aktuális elemmel lehet végezni. A lista rendelkezik az alábbi műveletekkel: Üres: Lista
Algoritmusok és adatszerkezetek I. 4. előadás A lista olyan sorozat, amelyben műveleteket egy kiválasztott, az ún. aktuális elemmel lehet végezni. A lista rendelkezik az alábbi műveletekkel: Üres: Lista
Tartalom Keresés és rendezés. Vektoralgoritmusok. 1. fejezet. Keresés adatvektorban. A programozás alapjai I.
 Keresés Rendezés Feladat Keresés Rendezés Feladat Tartalom Keresés és rendezés A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán
Keresés Rendezés Feladat Keresés Rendezés Feladat Tartalom Keresés és rendezés A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán
Keresés és rendezés. A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán
 Keresés Rendezés Feladat Keresés és rendezés A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán 2016. november 7. Farkas B., Fiala
Keresés Rendezés Feladat Keresés és rendezés A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán 2016. november 7. Farkas B., Fiala
Amortizációs költségelemzés
 Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Generikus osztályok, gyűjtemények és algoritmusok
 Programozási, gyűjtemények és algoritmusok bejárása Informatikai Kar Eötvös Loránd Tudományegyetem 1 Tartalom 1 bejárása 2 bejárása 2 Java-ban és UML-ben bejárása Az UML-beli paraméteres osztályok a Java
Programozási, gyűjtemények és algoritmusok bejárása Informatikai Kar Eötvös Loránd Tudományegyetem 1 Tartalom 1 bejárása 2 bejárása 2 Java-ban és UML-ben bejárása Az UML-beli paraméteres osztályok a Java
17. A 2-3 fák és B-fák. 2-3 fák
 17. A 2-3 fák és B-fák 2-3 fák Fontos jelentősége, hogy belőlük fejlődtek ki a B-fák. Def.: Minden belső csúcsnak 2 vagy 3 gyermeke van. A levelek egy szinten helyezkednek el. Az adatrekordok/kulcsok csak
17. A 2-3 fák és B-fák 2-3 fák Fontos jelentősége, hogy belőlük fejlődtek ki a B-fák. Def.: Minden belső csúcsnak 2 vagy 3 gyermeke van. A levelek egy szinten helyezkednek el. Az adatrekordok/kulcsok csak
Pásztor Attila. Algoritmizálás és programozás tankönyv az emeltszintű érettségihez
 Pásztor Attila Algoritmizálás és programozás tankönyv az emeltszintű érettségihez 3. ADATTÍPUSOK...26 3.1. AZ ADATOK LEGFONTOSABB JELLEMZŐI:...26 3.2. ELEMI ADATTÍPUSOK...27 3.3. ÖSSZETETT ADATTÍPUSOK...28
Pásztor Attila Algoritmizálás és programozás tankönyv az emeltszintű érettségihez 3. ADATTÍPUSOK...26 3.1. AZ ADATOK LEGFONTOSABB JELLEMZŐI:...26 3.2. ELEMI ADATTÍPUSOK...27 3.3. ÖSSZETETT ADATTÍPUSOK...28
Algoritmusok és adatszerkezetek gyakorlat 07
 Algoritmusok és adatszerkezetek gyakorlat 0 Keresőfák Fák Fa: összefüggő, körmentes gráf, melyre igaz, hogy: - (Általában) egy gyökér csúcsa van, melynek 0 vagy több részfája van - Pontosan egy út vezet
Algoritmusok és adatszerkezetek gyakorlat 0 Keresőfák Fák Fa: összefüggő, körmentes gráf, melyre igaz, hogy: - (Általában) egy gyökér csúcsa van, melynek 0 vagy több részfája van - Pontosan egy út vezet
6. előadás. Kiegyensúlyozottság, AVL-fa, piros-fekete fa. Adatszerkezetek és algoritmusok előadás március 6.
 6. előadás, AVL-fa, piros-fekete fa Adatszerkezetek és algoritmusok előadás 2018. március 6.,, és Debreceni Egyetem Informatikai Kar 6.1 Általános tudnivalók Ajánlott irodalom: Thomas H. Cormen, Charles
6. előadás, AVL-fa, piros-fekete fa Adatszerkezetek és algoritmusok előadás 2018. március 6.,, és Debreceni Egyetem Informatikai Kar 6.1 Általános tudnivalók Ajánlott irodalom: Thomas H. Cormen, Charles
7. BINÁRIS FÁK 7.1. A bináris fa absztrakt adattípus 7.2. A bináris fa absztrakt adatszerkezet
 7. BINÁRIS FÁK Az előző fejezetekben már találkoztunk bináris fákkal. Ezt a központi fontosságú adatszerkezetet most vezetjük be a saját helyén és az általános fák szerepét szűkítve, csak a bináris fát
7. BINÁRIS FÁK Az előző fejezetekben már találkoztunk bináris fákkal. Ezt a központi fontosságú adatszerkezetet most vezetjük be a saját helyén és az általános fák szerepét szűkítve, csak a bináris fát
Programozási technológia
 Programozási technológia Generikus osztályok Gyűjtemények Dr. Szendrei Rudolf ELTE Informatikai Kar 2018. Generikus osztályok Javaban az UML paraméteres osztályainak a generikus (sablon) osztályok felelnek
Programozási technológia Generikus osztályok Gyűjtemények Dr. Szendrei Rudolf ELTE Informatikai Kar 2018. Generikus osztályok Javaban az UML paraméteres osztályainak a generikus (sablon) osztályok felelnek
Adatszerkezetek és algoritmusok
 2010. január 8. Bevezet El z órák anyagainak áttekintése Ismétlés Adatszerkezetek osztályozása Sor, Verem, Lengyelforma Statikus, tömbös reprezentáció Dinamikus, láncolt reprezentáció Láncolt lista Lassú
2010. január 8. Bevezet El z órák anyagainak áttekintése Ismétlés Adatszerkezetek osztályozása Sor, Verem, Lengyelforma Statikus, tömbös reprezentáció Dinamikus, láncolt reprezentáció Láncolt lista Lassú
Adatszerkezetek I. 7. előadás. (Horváth Gyula anyagai felhasználásával)
 Adatszerkezetek I. 7. előadás (Horváth Gyula anyagai felhasználásával) Bináris fa A fa (bináris fa) rekurzív adatszerkezet: BinFa:= Fa := ÜresFa Rekord(Elem,BinFa,BinFa) ÜresFa Rekord(Elem,Fák) 2/37 Bináris
Adatszerkezetek I. 7. előadás (Horváth Gyula anyagai felhasználásával) Bináris fa A fa (bináris fa) rekurzív adatszerkezet: BinFa:= Fa := ÜresFa Rekord(Elem,BinFa,BinFa) ÜresFa Rekord(Elem,Fák) 2/37 Bináris
Gráfok 1. Tárolási módok, bejárások. Szoftvertervezés és -fejlesztés II. előadás. Szénási Sándor
 Gráfok 1. Tárolási módok, bejárások előadás http://nik.uni-obuda.hu/sztf2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Gráfok 1. Tárolási módok Szélességi
Gráfok 1. Tárolási módok, bejárások előadás http://nik.uni-obuda.hu/sztf2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Gráfok 1. Tárolási módok Szélességi
Rekurzió. Dr. Iványi Péter
 Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Algoritmuselmélet. 2-3 fák. Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem. 8.
 Algoritmuselmélet 2-3 fák Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 8. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet 8. előadás
Algoritmuselmélet 2-3 fák Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 8. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet 8. előadás
7 7, ,22 13,22 13, ,28
 Általános keresőfák 7 7,13 13 13 7 20 7 20,22 13,22 13,22 7 20 25 7 20 25,28 Általános keresőfa Az általános keresőfa olyan absztrakt adatszerkezet, amely fa és minden cellájában nem csak egy (adat), hanem
Általános keresőfák 7 7,13 13 13 7 20 7 20,22 13,22 13,22 7 20 25 7 20 25,28 Általános keresőfa Az általános keresőfa olyan absztrakt adatszerkezet, amely fa és minden cellájában nem csak egy (adat), hanem
Adatszerkezetek 2. Dr. Iványi Péter
 Adatszerkezetek 2. Dr. Iványi Péter 1 Hash tábla A bináris fáknál O(log n) a legjobb eset a keresésre. Ha valamilyen közvetlen címzést használunk, akkor akár O(1) is elérhető. A hash tábla a tömb általánosításaként
Adatszerkezetek 2. Dr. Iványi Péter 1 Hash tábla A bináris fáknál O(log n) a legjobb eset a keresésre. Ha valamilyen közvetlen címzést használunk, akkor akár O(1) is elérhető. A hash tábla a tömb általánosításaként
Programozás alapjai. 8. előadás
 8. előadás Wagner György Általános Informatikai Tanszék Azonosítók érvényességi köre Kiindulási alap: a blokkszerkezetű programozási nyelvek (C, FORTRAN, PASCAL, ) Egy program szerkezete: Fejléc Deklarációsrész
8. előadás Wagner György Általános Informatikai Tanszék Azonosítók érvényességi köre Kiindulási alap: a blokkszerkezetű programozási nyelvek (C, FORTRAN, PASCAL, ) Egy program szerkezete: Fejléc Deklarációsrész
Tartalomjegyzék. Köszönetnyilvánítás. 1. Az alapok 1
 Köszönetnyilvánítás Bevezetés Kinek szól a könyv? Elvárt előismeretek A könyv témája A könyv használata A megközelítés alapelvei Törekedjünk az egyszerűségre! Ne optimalizáljunk előre! Felhasználói interfészek
Köszönetnyilvánítás Bevezetés Kinek szól a könyv? Elvárt előismeretek A könyv témája A könyv használata A megközelítés alapelvei Törekedjünk az egyszerűségre! Ne optimalizáljunk előre! Felhasználói interfészek
Adatszerkezetek és algoritmusok
 2009. november 20. Bevezet El z órák anyagainak áttekintése Ismétlés Adatszerkezetek osztályozása Sor, Verem, Lengyelforma Statikus, tömbös reprezentáció Dinamikus, láncolt reprezentáció El z órák anyagainak
2009. november 20. Bevezet El z órák anyagainak áttekintése Ismétlés Adatszerkezetek osztályozása Sor, Verem, Lengyelforma Statikus, tömbös reprezentáció Dinamikus, láncolt reprezentáció El z órák anyagainak
Algoritmizálás. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar
 Algoritmizálás Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar horvath@inf.u-szeged.hu 0.1. Az algoritmikus tudás szintjei Ismeri (a megoldó algoritmust) Érti Le tudja pontosan
Algoritmizálás Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar horvath@inf.u-szeged.hu 0.1. Az algoritmikus tudás szintjei Ismeri (a megoldó algoritmust) Érti Le tudja pontosan
Adatszerkezetek. Nevezetes algoritmusok (Keresések, rendezések)
 Adatszerkezetek Nevezetes algoritmusok (Keresések, rendezések) Keresések A probléma általános megfogalmazása: Adott egy N elemű sorozat, keressük meg azt az elemet (határozzuk meg a helyét a sorozatban),
Adatszerkezetek Nevezetes algoritmusok (Keresések, rendezések) Keresések A probléma általános megfogalmazása: Adott egy N elemű sorozat, keressük meg azt az elemet (határozzuk meg a helyét a sorozatban),
Ugrólisták. RSL Insert Example. insert(22) with 3 flips. Runtime?
 Ugrólisták Ugrólisták Ugrólisták Ugrólisták RSL Insert Example insert(22) with 3 flips 13 8 29 20 10 23 19 11 2 13 22 8 29 20 10 23 19 11 2 Runtime? Ugrólisták Empirical analysis http://www.inf.u-szeged.hu/~tnemeth/alga2/eloadasok/skiplists.pdf
Ugrólisták Ugrólisták Ugrólisták Ugrólisták RSL Insert Example insert(22) with 3 flips 13 8 29 20 10 23 19 11 2 13 22 8 29 20 10 23 19 11 2 Runtime? Ugrólisták Empirical analysis http://www.inf.u-szeged.hu/~tnemeth/alga2/eloadasok/skiplists.pdf
adatszerkezetek 2007/7/6 15:51 page 27 #23
 adatszerkezetek 2007/7/6 15:51 page 27 #23 9. FEJEZET Állományok 9.1. Alapfogalmak 9.1. definíció. Másodlagos tárolónak vagy külső tárolónak, háttértárnak, periféria tárolónak nevezzük azokat a tárolóeszközöket,
adatszerkezetek 2007/7/6 15:51 page 27 #23 9. FEJEZET Állományok 9.1. Alapfogalmak 9.1. definíció. Másodlagos tárolónak vagy külső tárolónak, háttértárnak, periféria tárolónak nevezzük azokat a tárolóeszközöket,
Adatszerkezetek I. 1. előadás
 Adatszerkezetek I. 1. előadás Adatok jellemzői ismétlés 1. Azonosító Az a jelsorozat, amellyel hivatkozhatunk a tartalmára, amely által módosíthatjuk tartalmát. 2. Hozzáférési jog Adatokat módosítani,
Adatszerkezetek I. 1. előadás Adatok jellemzői ismétlés 1. Azonosító Az a jelsorozat, amellyel hivatkozhatunk a tartalmára, amely által módosíthatjuk tartalmát. 2. Hozzáférési jog Adatokat módosítani,
ADATSZERKEZETEK (VEREM, SOR)
 ADATSZERKEZETEK (VEREM, SOR) 1. ADATSZERKEZET FOGALMA Az adatszerkezet egymással kapcsolatban álló adatok összessége, amelyen meghatározott, az adatszerkezetre jellemző műveletek végezhetők el. Az adatok
ADATSZERKEZETEK (VEREM, SOR) 1. ADATSZERKEZET FOGALMA Az adatszerkezet egymással kapcsolatban álló adatok összessége, amelyen meghatározott, az adatszerkezetre jellemző műveletek végezhetők el. Az adatok
Adatszerkezetek Tömb, sor, verem. Dr. Iványi Péter
 Adatszerkezetek Tömb, sor, verem Dr. Iványi Péter 1 Adat Adat minden, amit a számítógépünkben tárolunk és a külvilágból jön Az adatnak két fontos tulajdonsága van: Értéke Típusa 2 Adat típusa Az adatot
Adatszerkezetek Tömb, sor, verem Dr. Iványi Péter 1 Adat Adat minden, amit a számítógépünkben tárolunk és a külvilágból jön Az adatnak két fontos tulajdonsága van: Értéke Típusa 2 Adat típusa Az adatot
Programozás alapjai 9. előadás. Wagner György Általános Informatikai Tanszék
 9. előadás Wagner György Általános Informatikai Tanszék Leszámoló rendezés Elve: a rendezett listában a j-ik kulcs pontosan j-1 kulcsnál lesz nagyobb. (Ezért ha egy kulcsról tudjuk, hogy 27 másiknál nagyobb,
9. előadás Wagner György Általános Informatikai Tanszék Leszámoló rendezés Elve: a rendezett listában a j-ik kulcs pontosan j-1 kulcsnál lesz nagyobb. (Ezért ha egy kulcsról tudjuk, hogy 27 másiknál nagyobb,
Algoritmusok és adatszerkezetek I. 3. előadás
 Algoritmusok és adatszerkezetek I. 3. előadás Kupac A kupac olyan véges elemsokaság, amely rendelkezik az alábbi tulajdonságokkal: 1. Minden elemnek legfeljebb két rákövetkezője (leszármazottja) lehet.
Algoritmusok és adatszerkezetek I. 3. előadás Kupac A kupac olyan véges elemsokaság, amely rendelkezik az alábbi tulajdonságokkal: 1. Minden elemnek legfeljebb két rákövetkezője (leszármazottja) lehet.
ADATBÁZIS-KEZELÉS. Adatbázis-kezelő rendszerek
 ADATBÁZIS-KEZELÉS Adatbázis-kezelő rendszerek Adat (Data) Észlelhető, felfogható ismeret Jelsorozat Tény, közlés Valakinek vagy valaminek a jellemzője Adatbázis (Data Base, DB) Hosszú ideig évekig meglévő
ADATBÁZIS-KEZELÉS Adatbázis-kezelő rendszerek Adat (Data) Észlelhető, felfogható ismeret Jelsorozat Tény, közlés Valakinek vagy valaminek a jellemzője Adatbázis (Data Base, DB) Hosszú ideig évekig meglévő
Hasító táblázatok. Hasító függvények, kulcsütközés kezelése. Programozás II. előadás. Szénási Sándor
 Hasító táblázatok Hasító függvények, kulcsütközés kezelése előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Felépítése
Hasító táblázatok Hasító függvények, kulcsütközés kezelése előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Felépítése
21. Adatszerkezetek Az adattípus absztrakciós szintjei Absztrakt adattípus (ADT) Absztrakt adatszerkezet (ADS) Egyszerű adattípusok Tömbök
 2. Adatszerkezetek Az adattípus absztrakciós szintjei http://people.inf.elte.hu/fekete/docs_/adt_ads.pdf Absztrakt adattípus (ADT) Az adattípust úgy specifikáljuk, hogy szerkezetére, reprezentálására,
2. Adatszerkezetek Az adattípus absztrakciós szintjei http://people.inf.elte.hu/fekete/docs_/adt_ads.pdf Absztrakt adattípus (ADT) Az adattípust úgy specifikáljuk, hogy szerkezetére, reprezentálására,
Adatszerkezetek 7a. Dr. IványiPéter
 Adatszerkezetek 7a. Dr. IványiPéter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér () Nincsennek hurkok!!! 2 Bináris fák Azokat a
Adatszerkezetek 7a. Dr. IványiPéter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér () Nincsennek hurkok!!! 2 Bináris fák Azokat a
C++ programozási nyelv
 C++ programozási nyelv Gyakorlat - 13. hét Nyugat-Magyarországi Egyetem Faipari Mérnöki Kar Informatikai Intézet Soós Sándor 2004. december A C++ programozási nyelv Soós Sándor 1/10 Tartalomjegyzék Objektumok
C++ programozási nyelv Gyakorlat - 13. hét Nyugat-Magyarországi Egyetem Faipari Mérnöki Kar Informatikai Intézet Soós Sándor 2004. december A C++ programozási nyelv Soós Sándor 1/10 Tartalomjegyzék Objektumok
3. TÖMBÖK A tömb absztrakt adattípus Legyen T az E alaptípus feletti k ( 1) dimenziós tömb típus. Vezessük be az I I1
 3. TÖMBÖK Az egyszerű adattípusok ismertetését a tömbökkel kezdjük. Az sem okozna zavart, ha ezt a fejezet nem szerepelne jegyzetünkben, tekintettel arra, hogy a tömböket ismerjük a programozási kurzusokból.
3. TÖMBÖK Az egyszerű adattípusok ismertetését a tömbökkel kezdjük. Az sem okozna zavart, ha ezt a fejezet nem szerepelne jegyzetünkben, tekintettel arra, hogy a tömböket ismerjük a programozási kurzusokból.
Digitális technika VIMIAA01
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek
Hierarchikus adatszerkezetek
 Hierarchikus adatszerkezetek A szekveniális adatszerkezetek általánosítása. Minden adatelemnek pontosan 1 megelőzője van, de akárhány rákövetkezője lehet, kivéve egy speciális elemet. Fa (tree) Hierarchikus
Hierarchikus adatszerkezetek A szekveniális adatszerkezetek általánosítása. Minden adatelemnek pontosan 1 megelőzője van, de akárhány rákövetkezője lehet, kivéve egy speciális elemet. Fa (tree) Hierarchikus
Programozási segédlet
 Programozási segédlet Programozási tételek Az alábbiakban leírtam néhány alap algoritmust, amit ismernie kell annak, aki programozásra adja a fejét. A lista korántsem teljes, ám ennyi elég kell legyen
Programozási segédlet Programozási tételek Az alábbiakban leírtam néhány alap algoritmust, amit ismernie kell annak, aki programozásra adja a fejét. A lista korántsem teljes, ám ennyi elég kell legyen
Belépés a GroupWise levelező rendszerbe az Internet felől
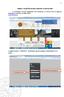 1 Belépés a GroupWise levelező rendszerbe az Internet felől A GroupWise levelező szolgáltatás web felelületről, az Internet felől az Egyetem honlapjáról is elérhető, az alábbi linken: www.uni-nke.hu WEBMAIL-NKE
1 Belépés a GroupWise levelező rendszerbe az Internet felől A GroupWise levelező szolgáltatás web felelületről, az Internet felől az Egyetem honlapjáról is elérhető, az alábbi linken: www.uni-nke.hu WEBMAIL-NKE
Adatszerkezetek Hasító táblák. Dr. Iványi Péter
 Adatszerkezetek Hasító táblák Dr. Iványi Péter 1 Hash tábla A bináris fáknál O(log n) a legjobb eset a keresésre. Ha valamilyen közvetlen címzést használunk, akkor akár O(1) is elérhető. A hash tábla a
Adatszerkezetek Hasító táblák Dr. Iványi Péter 1 Hash tábla A bináris fáknál O(log n) a legjobb eset a keresésre. Ha valamilyen közvetlen címzést használunk, akkor akár O(1) is elérhető. A hash tábla a
Adatszerkezetek és algoritmusok
 2009. november 13. Ismétlés El z órai anyagok áttekintése Ismétlés Specikáció Típusok, kifejezések, m veletek, adatok ábrázolása, típusabsztakció Vezérlési szerkezetek Függvények, paraméterátadás, rekurziók
2009. november 13. Ismétlés El z órai anyagok áttekintése Ismétlés Specikáció Típusok, kifejezések, m veletek, adatok ábrázolása, típusabsztakció Vezérlési szerkezetek Függvények, paraméterátadás, rekurziók
Érdekes informatika feladatok
 A keres,kkel és adatbázissal ellátott lengyel honlap számos díjat kapott: Spirit of Delphi '98, Delphi Community Award, Poland on the Internet, Golden Bagel Award stb. Az itt megtalálható komponenseket
A keres,kkel és adatbázissal ellátott lengyel honlap számos díjat kapott: Spirit of Delphi '98, Delphi Community Award, Poland on the Internet, Golden Bagel Award stb. Az itt megtalálható komponenseket
Adatszerkezetek 2. Dr. Iványi Péter
 Adatszerkezetek 2. Dr. Iványi Péter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér (root) Nincsennek hurkok!!! 2 Bináris fák Azokat
Adatszerkezetek 2. Dr. Iványi Péter 1 Fák Fákat akkor használunk, ha az adatok között valamilyen alá- és fölérendeltség van. Pl. könyvtárszerkezet gyökér (root) Nincsennek hurkok!!! 2 Bináris fák Azokat
Információs Technológia
 Információs Technológia Sor és verem adatszerkezet Fodor Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék foa@almos.vein.hu 2009. november 19. Alapötlet
Információs Technológia Sor és verem adatszerkezet Fodor Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék foa@almos.vein.hu 2009. november 19. Alapötlet
10. tétel. Adatszerkezetek és algoritmusok vizsga Frissült: 2013. január 28.
 10. tétel Adatszerkezetek és algoritmusok vizsga Frissült: 2013. január 28. 2-3 fák Hatékony keresőfa-konstrukció. Ez is fa, de a binárisnál annyival bonyolultabb hogy egy nem-levél csúcsnak 2 vagy 3 fia
10. tétel Adatszerkezetek és algoritmusok vizsga Frissült: 2013. január 28. 2-3 fák Hatékony keresőfa-konstrukció. Ez is fa, de a binárisnál annyival bonyolultabb hogy egy nem-levél csúcsnak 2 vagy 3 fia
2018, Diszkrét matematika
 Diszkrét matematika 3. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: természetes
Diszkrét matematika 3. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: természetes
Java és web programozás
 Budapesti Műszaki Egyetem 2015. 02. 11. 2. Előadás Mese Néhány programozási módszer: Idők kezdetén való programozás Struktúrált Moduláris Funkcionális Objektum-orientált... Mese Néhány programozási módszer:
Budapesti Műszaki Egyetem 2015. 02. 11. 2. Előadás Mese Néhány programozási módszer: Idők kezdetén való programozás Struktúrált Moduláris Funkcionális Objektum-orientált... Mese Néhány programozási módszer:
Bánsághi Anna 2014 Bánsághi Anna 1 of 68
 IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 3. ELŐADÁS - PROGRAMOZÁSI TÉTELEK 2014 Bánsághi Anna 1 of 68 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 3. ELŐADÁS - PROGRAMOZÁSI TÉTELEK 2014 Bánsághi Anna 1 of 68 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
Elemi adatszerkezetek
 2017/12/16 17:22 1/18 Elemi adatszerkezetek < Programozás Elemi adatszerkezetek Szerző: Sallai András Copyright Sallai András, 2011, 2014 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu
2017/12/16 17:22 1/18 Elemi adatszerkezetek < Programozás Elemi adatszerkezetek Szerző: Sallai András Copyright Sallai András, 2011, 2014 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu
file:///d:/okt/ad/jegyzet/ad1/b+fa.html
 1 / 5 2016. 11. 30. 12:58 B+ fák CSci 340: Database & Web systems Home Syllabus Readings Assignments Tests Links Computer Science Hendrix College Az alábbiakban Dr. Carl Burch B+-trees című Internetes
1 / 5 2016. 11. 30. 12:58 B+ fák CSci 340: Database & Web systems Home Syllabus Readings Assignments Tests Links Computer Science Hendrix College Az alábbiakban Dr. Carl Burch B+-trees című Internetes
Adatszerkezetek I. 4. előadás
 Adatszerkezetek I. 4. előadás Kupac A kupac olyan véges elemsokaság, amely rendelkezik az alábbi tulajdonságokkal: 1. Minden elemnek legfeljebb két rákövetkezője (leszármazottja) lehet. Azaz bináris fának
Adatszerkezetek I. 4. előadás Kupac A kupac olyan véges elemsokaság, amely rendelkezik az alábbi tulajdonságokkal: 1. Minden elemnek legfeljebb két rákövetkezője (leszármazottja) lehet. Azaz bináris fának
Fejlesztési specifikációk
 Fejlesztési specifikációk Általános követelmények 1. A feladatok leírása csak a tárolandó adatokat tartalmazza. A szükséges táblákat (beleértve a törzs vagy szótár táblákat) a programozóknak kell megtervezni
Fejlesztési specifikációk Általános követelmények 1. A feladatok leírása csak a tárolandó adatokat tartalmazza. A szükséges táblákat (beleértve a törzs vagy szótár táblákat) a programozóknak kell megtervezni
Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel. Az objektumok áthaladnak a többi objektumon
 Bevezetés Ütközés detektálás Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel Az objektumok áthaladnak a többi objektumon A valósághű megjelenítés része Nem tisztán
Bevezetés Ütközés detektálás Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel Az objektumok áthaladnak a többi objektumon A valósághű megjelenítés része Nem tisztán
Pénzügyi algoritmusok
 Pénzügyi algoritmusok A C++ programozás alapjai Sztringek Osztályok alapjai Sztringek Szöveges adatok kezelése Sztring Karakterlánc (string): Szöveges adat Karaktertömbként tárolva A szöveg végét a speciális
Pénzügyi algoritmusok A C++ programozás alapjai Sztringek Osztályok alapjai Sztringek Szöveges adatok kezelése Sztring Karakterlánc (string): Szöveges adat Karaktertömbként tárolva A szöveg végét a speciális
(Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja.
 Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is
 A tétel (record) tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is A tétel elemei mezők. Például tétel: személy elemei: név, lakcím, születési
A tétel (record) tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is A tétel elemei mezők. Például tétel: személy elemei: név, lakcím, születési
9. Állományok kezelése. Operációs rendszerek. Állomány (file) Könyvtár. Az állománykezelő feladatai. Az állományrendszer réteges implementációja
 Operációs rendszerek 9. Állományok kezelése Simon Gyula Felhasznált irodalom: Kóczy-Kondorosi (szerk.): Operációs rendszerek mérnöki megközelítésben Tanenbaum: Modern Operating Systems 2nd. Ed. Silberschatz,
Operációs rendszerek 9. Állományok kezelése Simon Gyula Felhasznált irodalom: Kóczy-Kondorosi (szerk.): Operációs rendszerek mérnöki megközelítésben Tanenbaum: Modern Operating Systems 2nd. Ed. Silberschatz,
Láncolt lista. az itt adott nevet csak a struct deklaráción belül használjuk
 Láncolt lista int szam char szoveg[10] következő elemre mutató pointer int szam char szoveg[10] következő elemre mutató pointer elem elem elem int szam char szoveg[10] következő elemre mutató pointer A
Láncolt lista int szam char szoveg[10] következő elemre mutató pointer int szam char szoveg[10] következő elemre mutató pointer elem elem elem int szam char szoveg[10] következő elemre mutató pointer A
Objektum Orientált Szoftverfejlesztés (jegyzet)
 Objektum Orientált Szoftverfejlesztés (jegyzet) 1. Kialakulás Kísérletek a szoftverkrízisből való kilábalásra: 1.1 Strukturált programozás Ötlet (E. W. Dijkstra): 1. Elkészítendő programot elgondolhatjuk
Objektum Orientált Szoftverfejlesztés (jegyzet) 1. Kialakulás Kísérletek a szoftverkrízisből való kilábalásra: 1.1 Strukturált programozás Ötlet (E. W. Dijkstra): 1. Elkészítendő programot elgondolhatjuk
Adatszerkezetek I. 6. előadás
 Adatszerkezetek I. 6. előadás Táblázat A táblázat olyan halmazféleség, amelyben az elemeket kulcsértékkel azonosítjuk. A szokásos halmazműveletekből azonban csak néhányat definiálunk rá: Üres: Táblázat
Adatszerkezetek I. 6. előadás Táblázat A táblázat olyan halmazféleség, amelyben az elemeket kulcsértékkel azonosítjuk. A szokásos halmazműveletekből azonban csak néhányat definiálunk rá: Üres: Táblázat
Programozás alapjai. 10. előadás
 10. előadás Wagner György Általános Informatikai Tanszék Pointerek, dinamikus memóriakezelés A PC-s Pascal (is) az IBM PC memóriáját 4 fő részre osztja: kódszegmens adatszegmens stackszegmens heap Alapja:
10. előadás Wagner György Általános Informatikai Tanszék Pointerek, dinamikus memóriakezelés A PC-s Pascal (is) az IBM PC memóriáját 4 fő részre osztja: kódszegmens adatszegmens stackszegmens heap Alapja:
Algoritmusok és adatszerkezetek I. 5. előadás
 Algoritmusok és adatszerkezetek I. 5. előadás Táblázat A táblázat olyan halmazféleség, amelyben az elemeket kulcsértékkel azonosítjuk. A szokásos halmazműveletekből azonban csak néhányat definiálunk rá:
Algoritmusok és adatszerkezetek I. 5. előadás Táblázat A táblázat olyan halmazféleség, amelyben az elemeket kulcsértékkel azonosítjuk. A szokásos halmazműveletekből azonban csak néhányat definiálunk rá:
Például számokból álló, egyszeresen láncolt lista felépítéséhez az alábbi struktúra definíciót használhatjuk:
 8. előadás Ismétlés Dinamikus adatszerkezetek: listák (egyszeresen vagy többszörösen láncolt), fák. Kétfelé ágazó fa: bináris fa Dinamikus adatszerkezetek - önhivatkozó adatstruktúrák: adatok és reájuk
8. előadás Ismétlés Dinamikus adatszerkezetek: listák (egyszeresen vagy többszörösen láncolt), fák. Kétfelé ágazó fa: bináris fa Dinamikus adatszerkezetek - önhivatkozó adatstruktúrák: adatok és reájuk
2. AZ ADATTÍPUS ABSZTRAKCIÓS SZINTJEI
 2. AZ ADATTÍPUS ABSZTRAKCIÓS SZINTJEI Ebben a bevezető jellegű fejezetben arra a kérdésre próbálunk válaszolni, hogy az adattípusok, illetve adatszerkezetek milyen absztrakciós szinten jelennek meg az
2. AZ ADATTÍPUS ABSZTRAKCIÓS SZINTJEI Ebben a bevezető jellegű fejezetben arra a kérdésre próbálunk válaszolni, hogy az adattípusok, illetve adatszerkezetek milyen absztrakciós szinten jelennek meg az
