A NAPSUGÁRZÁS SPEKTRUMA ÉS AZ EMBERI SZEM ÉRZÉKENYSÉGE
|
|
|
- Emília Hegedüs
- 8 évvel ezelőtt
- Látták:
Átírás
1 A NAPSUGÁRZÁS SPEKTRUMA ÉS AZ EMBERI SZEM ÉRZÉKENYSÉGE Antal Ákos BME, Finommechanikai, Optikai Tanszék Kály-Kullai Kristóf, Farkas Henrik BME Kémiai Fizika Tanszék Aki tanulta fizikából a fekete test sugárzását, annak bizonyára ismerôsnek tûnnek a következô mondatok: A napfelszín hômérsékletének (kb. 6 K) megfelelô fekete sugárzás spektrális eloszlásának a maximuma körülbelül 55 nm. Ugyanitt van a maximuma a szem érzékenységi görbéjének is. Ez a két állítás együtt azt sugallja, hogy nem véletlenrôl van ám szó, a szem érzékenysége nyilván igazodott a Nap sugárzásához, arra optimalizálódott. Egyik legjellemzôbb példaként idézzünk egy magyar fordításban is megjelent tankönyvet [1]: A Nap feketetest-görbéje (152a. ábra) azt mutatja, hogy a kisugárzott energia 4%-a a látható tartományra jut, a fennmaradó energia legnagyobb része pedig a közeli infrabe Az emissziós csúcs figyelemreméltóan közel van az emberi szem érzékenységi maximumához (152b. ábra). A két görbe csúcsai elhelyezkedésének hasonlósága több véletlen egybeesésnél. Az ember fejlôdése során azok az egyedek kerültek kedvezôbb helyzetbe a természetes kiválasztódás folyamán, akiknek a szeme abban a színképtartományban volt a legérzékenyebb, amelyikben a legtöbb fény is volt. Így a fejlôdés folyamán általában az állati populációk válaszgörbéjének a csúcsa a Nap feketetest-görbéje csúcsának irányába tolódott el. Az idézett 152. ábra aláírása: a) A Nap felületérôl kisugárzott fény spektrális eloszlása; b) a szem válaszának spektrális eloszlása. A két függvény maximuma 55 nm környékén van. Megjegyezzük, hogy mindkét ábrán a hullámhossz van feltüntetve a vízszintes tengelyen. Másik példaként idézzünk egy, a közelmúltban megjelent, ugyancsak alapos optika tankönyvet [2]: A nappali látás V (λ) függvényének maximuma 555 nm-en van; ez megegyezik a Nap (központi égitestünk) spektrális sugárzási teljesítményének maximumhelyével! Ugyanakkor az esti látás V (λ) függvényének maximuma 57 nm-nél található, és ez az éjszakai hold- és csillagfények kékesebb teljesítményeloszlásának felel meg (21.7. ábra). Az interneten lévô friss anyagok között is találhatunk igen markáns megfogalmazásokat [3], a Wien-törvényt ismertetô résznél szerepel (magyar fordításban): a Nap sugárzásának maximuma a zöld színnél van (a szemünk erre a színre a legérzékenyebb). Az egyik legérdekesebb idézet e témával kapcsolatban a clevelandi Case Western Reserve University honlapján [4] található (magyar fordításban): A Nap sugárzására a maximum 51,4 nm-nél van, ami a látható spektrum zöld részébe esik. Ha azonban ránézünk (amit persze sohase tegyünk, mert a szem károsodhat!), a Nap inkább sárgának látszik. Eddig senkinek sem sikerült megmagyaráznia, hogy miért tûnik a Nap sárgának ahelyett, hogy zöld lenne. Azonban érdekes tény, hogy szemünk körülbelül ilyen hullámhosszú zöld fényt lát a legjobban. Más tankönyvek ennél sokkal árnyaltabban fogalmaznak. Megtartják ugyan a Nap szemre gyakorolt hatásának legalábbis hallgatólagos feltételezését, de nem a két spektrum maximumhelyének azonosságát hangsúlyozzák, hanem gyakran megelégednek lazább megfogalmazással, például, hogy a spektrum maximuma a látható tartomány közepére esik. Egy ilyen árnyaltabb megfogalmazásra példa a következô [5]: a szem ezen érzékenységi görbéje összefüggésbe hozható érzékelô szerveink hosszan tartó alkalmazkodásával a bolygónkon uralkodó körülményekhez, ahol is a legfényesebb fényforrás mindig is a Nap volt. A tankönyvek, oktatási anyagok, szakirodalmak döntô többsége abban viszont közös, hogy a spektrumokat hullámhossz szerinti felbontásban ábrázolják. Az, hogy az evolúció során a Nap sugárzásának befolyása volt az emberi szem érzékenységének alakulására, kézenfekvô, racionális gondolat. Az viszont, hogy mindezt a hullámhossz szerinti spektrum maximumának helyébôl olvassák ki, már erôsen kifogásolható. A továbbiakban kimutatjuk, hogy a hagyományos megfogalmazás, nevezetesen a spektrum maximumának és a szem érzékenységére jellemzô láthatósági görbe (más néven érzékenységi spektrum) maximumának egybeesése mivel az a hullámhosszhoz tartozó spektrum A. NUSSBAUM, R.A. PHILLIPS: Modern optika mérnököknek és kutatóknak címû könyvébôl idézett 152. ábra F. JENKINS ET AL.: Optika címû könyvében szereplô 21.7 ábra ANTAL ÁKOS, KÁLY-KULLAI KRISTÓF, FARKAS HENRIK: A NAPSUGÁRZÁS SPEKTRUMA ÉS AZ EMBERI SZEM ÉRZÉKENYSÉGE 199
2 jellemzôje erôsen vitatható, bizonytalan megalapozottságú érv. Kísérletet teszünk a napsugárzás spektruma és az emberi szem érzékenységi görbéje között egy egyértelmûbb kapcsolat megállapítására. Spektrális eloszlás: mi a független változó? A spektrumokkal kapcsolatos irodalomban, még a modern irodalomban is, a hullámhossz szerinti felbontás elôfordulási gyakorisága magasan megelôzi a frekvencia szerinti felbontásét. Ez nyilván csak tradicionális okok miatt van így, hiszen a frekvencia fizikailag sokkal alapvetôbb jellemzôje az elektromágneses hullámoknak, mint a hullámhossz: a frekvencia megmarad, a hullámhossz pedig változik a közeghatáron való áthaladásnál vagy inhomogén közegben történô terjedésnél. Legyen (ν) egy elektromágneses sugárzás spektrális sûrûségfüggvénye, ahol ν a frekvencia. Ez azt jelenti, hogy a sugárzás intenzitása, az egységnyi felületre vonatkoztatott sugárzási teljesítmény (ν) dν. Bontsuk most föl ezt a sugárzást a frekvencia valamilyen függvénye szerint, azaz legyen adva egy kölcsönösen egyértelmû z = z (ν) függvény, és adjuk meg a sugárzás E z spektrumát a z független változó szerint: ahol E z = z() (ν) dν = ± z() E z (z) dz, (ν) dν/dz > ; dν/dz. (ν) dν/dz Tehát amiatt, hogy a ν skálája nem egyezik meg a z skálájával, a két spektrális sûrûségfüggvény eltér: bejön egy dν/dz nem állandó szorzófaktor. Ezért az E z, illetve spektrális eloszlások alakja eltér egymástól, emiatt a spektrum maximuma sem invariáns erre a transzformációra, a z szerinti eloszlás maximuma eltér a ν szerinti eloszlás maximumától, más a maximum értéke és máshol van a maximum helye is! Nézzük például a frekvencia és a hullámhossz közti transzformációt, azaz legyen z = λ = c /ν! A sugárzás intenzitása a hullámhossz szerinti spektrális eloszlásból ahol a spektrális eloszlás sûrûségfüggvénye E λ dλ, E λ = c λ 2. Az 1. ábrából leolvasható, hogy növekvô frekvenciatartományokban az egységnyi hullámhossztartomány a (1) (2) (3) (4) (5) λ (1 nm) ábra. A frekvencia és a hullámhossz skálája elektromágneses sugárzásnál vákuumban ν (114 Hz) spektrum egyre nagyobb részét fedi le. Az (5) formulából következik, hogy az E λ a magasabb frekvenciáknál nagyobb faktorral tér el -tôl, tehát a hullámhossz szerinti maximumnak nagyobb frekvencia felel meg, mint a frekvencia szerinti maximumnak. Ha a maximum a látható tartományban van, akkor a hullámhossz szerinti maximum az ibolya felé tolódik el a frekvencia szerinti maximumhoz képest. A fekete test sugárzásának spektruma A fekete test sugárzásának spektrális intenzitása, azaz az egységnyi felületre, egységnyi idôre, egységnyi frekvenciatartományra és 2π térszögre jutó kisugárzott spektrális energia, a spektrális emisszió (a sugárzás spektrális intenzitása): = 2 π h c 2 ν 3 e hν / kt 1. Ez Planck sugárzási törvénye [6, 7]. (Megjegyezzük, hogy a különbözô tankönyvekben a fenti alak helyett olyanok is elôfordulnak, amelyekben a 2π állandó helyett más szerepel. Az eltérés egyik oka lehet, hogy a vonatkoztatási térszög nem 2π, hanem 1, π, vagy 4π. Másik ok lehet, hogy néha a = h/2π jelölést használják h helyett. Mindez nem érinti a sugárzási görbe alakját.) Ha a szélsôérték helyére vagyunk kíváncsiak, akkor elegendô vizsgálnunk az E x (x) =K x 3 e x 1 függvényt, ahol K állandó. E függvénynek x 1 -nél maximuma van, ahol x 1 az x 1 3 e x 1 =3 nem algebrai (transzcendens) egyenlet gyöke, körülbelül 2,82. Áttérve az y =1/x változóra, a spektrális eloszlásfüggvény E y = K y 5 1 e 1/y 1. Ennek viszont y 2 -nél van maximuma, ahol y 2 az 1 y 2 5 e 1/y 2 =5 egyenlet gyöke. A megfelelô x 2 =1/y 2 értéke: x 2 = 4,96. A két maximumhely tehát jelentôsen eltér egymástól, a frekvencia szerinti maximum a közeli infra, a hullámhossz szerinti maximum pedig a kék tartományba (6) (7) (8) (9) (1) 2 NEM ÉLHETÜNK FIZIKA NÉLKÜL FIZIKAI SZEMLE 25 / 6
3 ν a (THz) λ a (nm) ν m (THz) λ m (nm) színe ν b (THz) λ b (nm) 1. táblázat A különbözô spektrális maximumok és láthatósági tartományok összevetése a tapasztalati értékekkel (1 THz =1 12 Hz) infra (világos)kék esik, annak is a nagyobb hullámhosszú részére, amit [8] világoskéknek (light blue) nevez, tehát a világos elôtag nem a telítettségre, hanem a frekvenciára utal. A gyakorlatban gyakran célszerû logaritmikus skálát használni. Bevezetve a w =lnx új skálát, az E w spektrális eloszlása sárgászöld A) A frekvencia szerinti spektrális eloszlás maximumából számolt adatok. B) A hullámhossz szerinti spektrum maximumából számot adatok. C) A logaritmikus skálából számolt adatok. D) Az energiahasznosítás optimumából számolt adatok. E) A fotometriában nemzetközileg elfogadott láthatósági görbébôl [11] vett adatok. Az indexek jelentése a ν frekvenciáknál és a λ hullámhosszaknál: a: a tartomány felé esô határa, b: a tartomány ibolya felé esô határa, m: a tartomány határainak geometriai közepe, tehát az alsó határ 2 1/2 -szerese, kivéve az E oszlopot, ahol ez a láthatósági görbe maximumhelye. E w = xe x = K x 4 e x 1. E függvény maximuma x w -nél van, ahol x w az (11) szuper-, sôt szubharmonikus rezonancia is, a sajátfrekvencia n -szereseinél, illetve n -edrészénél is, ahol n egész szám [1]. Különbözô hangforrások által keltett hanghullámoknál, például húrok és sípok esetén, már lineáris esetben is megjelennek felhangok. Infra abszorpciós spektrumokban egy csúcs mellett gyakran megfigyelhetô egy gyengébb csúcs ( felharmonikus sáv ) is. Mindezek alapján elképzelhetô, hogy a látásban szerepet játszó tényezôknél is elôfordulhat, hogy ha egy adott frekvenciára érzékeny egy bizonyos érzékelô, akkor ugyanaz a kétszeres frekvenciájú fényt is érzékeli. Ha a láthatósági tartomány oktávnál nagyobb lenne, akkor elôfordulhatna, hogy a szem nem tudná megkülönböztetni a kétszeres frekvenciájú jelet, tehát egyfajta színtévesztés fordulhatna elô. Valóban, szubjektív színérzetünk szerint a tôl távolodva a spektrumban, a színt a kékig távolodni érezzük, de az ibolyában mintha megint közelebb kerülnénk a höz, ugyanis az ibolyát a kék és színekbôl lehet kikeverni. A színmérésben használt papucsdiagram is tükrözi a spektrum két szélének viszonylagos közelségét [2]. Ezért kézenfekvô tekintenünk a következô optimalizációs problémát. Hol helyezzünk el egy oktáv szélességû ablakot a spektrumban (ez felelne meg a látható tartománynak) úgy, hogy ez az ablak a kisugárzott energia legnagyobb részét fedje le? Keressük tehát az x w 4 e x w =4 (12) egyenlet gyöke, x w = 3,92. A spektrum maximumának helyére alapozott érvelés tehát nem egyértelmû: nagyban függ a használt skálától. Nézzünk meg ezért most egy más típusú gondolatmenetet! Elôször is felhívjuk a figyelmet arra, hogy az emberi szemnél a spektrum látható tartománya mind a világosban, mind a sötétben való látás esetén körülbelül egy oktáv, a két végpont frekvenciájának aránya közel 2. Hasonló a helyzet a legtöbb állatnál, még akkor is, ha elôfordul látás az ultraibolya, illetve az infra tartományban is. Az embernél az eltérô spektrális típusú fotoreceptorok száma három, az állatoknál ez a szám ettôl különbözô lehet (emlôsöknél 2, lepkéknél 5, a sáskaráknál 112) [9]. A látás során több különbözô folyamat, mechanizmus, illetve többféle sejt játszik szerepet (a fény abszorbeálása, elektromos jellé, ingerületté alakítása, továbbítása, feldolgozása: ezeket végzik a fotoreceptorok, csapok, pálcikák, idegsejtek). Nem tisztázott, és ennek tisztázására mi sem vállalkozunk, hogy mi a pontos magyarázata e komplex folyamatban annak a tapasztalati ténynek, hogy az embernél és az állatok többségénél a látható tartomány körülbelül egy oktáv szélességû. Itt csak egy elképzelést, analóg példákat hozunk a fizikából ennek a ténynek egyik lehetséges magyarázatára. A lineáris oszcillátor gerjesztett rezgéseinél a rezonancia a sajátfrekvencia közelében fordul elô. Nemlineáris oszcillátorok gerjesztésénél viszont elôfordulhat 2ν 3a vagyis az azzal egyenértékû E ν dν = maximum, ν 3a 2x 3a x 3 x 3a e x dx = maximum 1 (13) (14) szélsôérték-probléma megoldását. A szélsôérték szükséges feltétele 2 2 x 3a 3 e 2 x 3a 1 = x 3 3a e x 3a 1, melybôl egyszerûsítéssel adódik e x 3a =15, (15) azaz x 3a = ln15 = 2,71. A megfelelô optimális tartomány határai tehát x 3a,x 3b =2x 3a. A tartomány közepének tekinthetjük a logaritmikus skálához igazodó geometriai közepet, azaz x 3 =2 1/2 x 3a, ekkor teljesül, hogy x 3b / x 3 = x 3 /x 3a. Ez a választás van összhangban azzal a megfigyeléssel, hogy egyes érzékszerveink skálája jó közelítéssel logaritmikus. A logaritmikus skála jelentôségét húzza alá a WeberFechner-féle pszichofizikai törvény: az ember érzetei (látás, hallás, tapintás) az ingerek logaritmusával arányosak. (Itt azonban ez csak analógia, mert itt nem az intenzitásról, hanem a frekvenciáról van szó.) ANTAL ÁKOS, KÁLY-KULLAI KRISTÓF, FARKAS HENRIK: A NAPSUGÁRZÁS SPEKTRUMA ÉS AZ EMBERI SZEM ÉRZÉKENYSÉGE 21
4 2. táblázat A sugárzás intenzitásának százalékos eloszlása a láthatósági ablakon belül és kívül 58 K hômérsékletû feketetest-sugárzás esetén a) 18, 5,2 34,3 32,9 43,1 m) 41,5 42,4 47,5 47,5 46,7 b) 4,5 7,4 18,2 19,6 1,2 A, B, C, D, E jelentése ugyanaz, mint az 1. táblázatban. a) Az ablakon kívüli, kisfrekvenciás sugárzás. m) Az ablakon belüli sugárzás. b) Az ablakon kívüli, nagyfrekvenciás sugárzás. Mindhárom adat az összintenzitás százalékában értendô. ν a (THz) λ a (nm) ν m (THz) λ m (nm) színe ν b (THz) λ b (nm) 3. táblázat A mért spektrummal végzett optimumszámítások adatai infra (világos)kék A jelölések magyarázata megtalálható az 1. táblázatnál A frekvencia és a hullámhossz szerinti maximumokhoz is hozzárendelhetünk egy megfelelô, oktáv szélességû látható tartományt oly módon, hogy a maximum helye az oktáv szélességû tartomány geometriai közepén legyen. Az így számolt látható tartományok egymással és a tényleges láthatósági adatokkal való összehasonlítását az 1. táblázat tartalmazza. A 2. táblázat azt mutatja, hogy a sugárzás intenzitása hogyan oszlik el a spektrumnak a láthatósági ablakon belüli és az azon kívüli részei között, 58 K hômérsékletû feketetest-sugárzásra sárgászöld táblázat Százalékos intenzitáseloszlások a mért spektrummal számolva a) 1,9 52,4 29,1 31,9 43,4 m) 4,5 46,2 56,5 57,6 53,4 b) 48,6 1,4 14,4 1,5 3,2 A jelölések magyarázata megtalálható az 1. és 2. táblázatnál. Az irodalomban hozzáférhetô napspektrumok nagy része csak a látható tartományra terjed ki, továbbá megkülönböztetik a direkt napsugárzásból, valamint a szórt, vagyis az égboltról jövô sugárzásból eredô spektrumokat. A számításokhoz az adatokat [12] a Renewable Resource Data Center honlapjáról vettük, és a global tilt oszlopot használtuk, amely az USA-ban tipikus besugárzásnak felel meg. A napsugárzás folytonos spektrumát a 2. ábra mutatja. A 3. táblázat összehasonlítja a háromféle optimumszámítás adatait. Elemzés A biofizikai irodalomban sok cikk foglalkozik azzal a kérdéssel, hogy az élôlények a napsugárzás elektromágneses spektrumának melyik részét hasznosítják, és miért éppen azt (lásd pl. [13, 14]). Egyik ismert jelenség, amely a láthatósági ablakkal kapcsolatos, a polarizációlátás UV-paradoxona: egyes rovarok a polarizált égboltfény UV-tartományát látják [15]. Nyilvánvalóan összefüggés van a földi élôlények fényérzékelése, így az emberi szem érzékenységi spektruma, és a napsugárzás között. Az az érvelés viszont nem meggyôzô, amely ezt az összefüggést a hullámhossz szerinti spektrális maximumhelyek közelségére alapozza. A hullámhossz szerinti spektrum használatát csak tradicionális okok magyarázzák. Az általunk javasolt követelmény, nevezetesen, hogy az oktáv szélességû láthatósági tartományt a hasznosított energia maximuma jelölje ki, független a skálától, hullámhossz, frekvencia vagy bármely más skálán is ugyanazt az eredményt kapjuk. Arra, hogy a hullámhossz szerinti spektrum és a frekvencia szerinti spektrum maximuma jelentôsen eltér egymástól, már régebben rámutattak, például Overduin [16]. Mint láttuk, a frekvencia szerinti maximum az infra tartomány felé tér el a láthatósági görbe maximumától. Overduin felvet egy másik lehetséges megközelítést, melyben a szemnek mint fotondetektornak az optimalizálását javasolja (a látásban hasznosított fotonok száma legyen maximális). Ha azt követelnénk meg, hogy a napsugárzásból hasznosított fotonok száma legyen maximális, akkor az (ν) függvényt, illetve ennek egy ablakban való integrálját kellene maximalizálni, az azonban még inkább a rossz irányba még kisebb frekvenciák felé tolódna el. 2. ábra. A Nap sugárzásának folytonos spektruma 2,5 A mért napsugárzás és az emberi szem érzékenységének kapcsolata a spektrumok alapján (ν) (1 11 J/m 2 ) 2 1,5 1, ν (1 15 Hz) 22 NEM ÉLHETÜNK FIZIKA NÉLKÜL FIZIKAI SZEMLE 25 / 6
5 Overduin is láthatósági ablak bevezetésével, az ezen ablakra vett integrál maximalizálásával véli felfedezni a helyes leírást, a napsugárzás és a szem érzékenysége közti kapcsolat magyarázatát. Ám okoskodása lényegében ugyanazt a hibát tartalmazza, ami a kifogás volt: ô is kitünteti a hullámhosszat a frekvenciához képest. A másik eltérés az itt közölt optimalizációs elképzeléstôl az, hogy ô az ablak abszolút szélességét veszi adottnak, mi pedig nem az intervallumot, hanem a végpontok arányát vesszük adottnak. Az 1. és a 3. táblázat összevetésével láthatjuk, hogy a különbözô optimalizálási követelményekbôl levonható következtetések közel azonosak mind az 58 K-es feketetest-sugárzásra, mind a számításainkhoz felhasznált mért napsugárzásra. Tehát a napsugárzás esetünkben is közelíthetô 58 K-es feketetest-sugárzással, ami régóta közismert. Arra, hogy a hullámhossz szerinti maximumokra alapozott érvelés jól illeszkedik a tényleges láthatósági görbéhez, sôt jobban, mint akár a frekvenciára, akár az energiaoptimumra alapozott érvelés, két magyarázat képzelhetô el: 1. Az evolúció során a látásra nem a fekete sugárzás, még csak nem is vagy pontosabban nemcsak a napspektrum gyakorolhatott döntô befolyást, hanem más tényezôk, például a konkrét környezetben lévô a létért való küzdelemben fontos másodlagos fényforrások által visszavert és szórt napfény, amelynek spektrális eloszlását legfeljebb becsülni lehetne. 2. A másik elképzelhetô, de általunk valószínûtlenebbnek tartott magyarázat szerint létezik valami olyan feltáratlan tényezô a látás mechanizmusában, amely a hullámhossz szerinti eloszlást kitüntetetté teszi például a frekvencia szerinti eloszláshoz képest is. Köszönetnyilvánítás A munkát részben az OTKA T-4278 számú pályázata támogatta. A szerzôk köszönetet mondanak Chris A. Gueymardnak, a Solar Consulting Services kutatóintézet (Edgewater, Florida, USA) kutatójának, Wenzel Klára egyetemi magántanárnak (BME, Mechatronika, Optika és Mûszertechnika Tanszék) és Verhás József egyetemi tanárnak (BME, Kémiai Fizika Tanszék) értékes segítségükért. Irodalom 1. A. NUSSBAUM, R.A. PHILLIPS: Modern optika mérnököknek és kutatóknak Mûszaki Könyvkiadó o., A mû eredeti címe: Contemporary Optics for Scientists and Engineers Prentice Hall Inc. 2. F. JENKINS ET AL.: Optika (szerk. Ábrahám György) Panem Kft., 1997, 473. o. 3. University of New Hampshire, Astronomy, Course Review, part Case Western Reserve University honlapja 5. N.I. KALITYEVSZKIJ: Volnovaja optyika Izdatyelsztvo Nauka, Moszkva 1971, 13. o. (orosz nyelven) 6. CSEREPES L., PETROVAI K.: Kozmikus fizika Egyetemi jegyzet, ELTE, 2. kiadás, Budapest, NAGY K.: Termodinamika és statisztikus mechanika Tankönyvkiadó, Budapest, C.A. GUEYMARD, H.D.KAMBEZIDIS: Solar Spectral Radiation in: T. Muneer et al.: Solar Radiation & Daylight Models 2nd ed., Elsevier, 24, Ch 5, MOLNÁR G., BLAHA B., HORVÁTH G.: Látás az ibolyán túl Természet Világa, április, BUDÓ Á.: Mechanika Tankönyvkiadó, Budapest, MSZ 962, Fénytechnikai terminológia 12. Renewable Resource Data Center honlapja: D.M. GATES Biophysical Ecology Springer-Verlag, HeidelbergBerlinNew York, G. HORVÁTH, J.GÁL, T.LABHART, R.WEHNER: Does reflection polarization by plants influence colour perception in insects? The Journal of Experimental Biology 25/21 (22) BARTA A., MIZERA F., HORVÁTH G.: Miért érdemes az égboltfény polarizációját az ultraibolyában érzékelni? Fizikai Szemle, 54 (24) J.M. OVERDUIN: Eyesight and the solar Wien peak Am. J. Phys. 71/3 (March 23) A POLIKRISTÁLYOS MEGSZILÁRDULÁS TÉRELMÉLETI MODELLEZÉSE Gránásy László, Pusztai Tamás, Börzsönyi Tamás MTA SZFKI, Budapest Legtöbb szerkezeti anyagunk polikristályos szerkezetû, azaz nagyszámú kristályszemcsébôl épül fel, amelyeknek méret, összetétel, alak stb. szerinti eloszlása, a mikroszerkezet határozza meg az adott anyag fizikai és korróziós tulajdonságait. A fémekkel kapcsolatos több ezer éves gyakorlat és a több mint száz évre visszatekintô tudományos vizsgálatok ellenére a polikristályos anyagok képzôdésének részletei csak kevéssé ismertek. A polikristályos anyagokat formálisan az alábbi két csoportba sorolhatjuk be: a) Anyagok, melyeket a nukleálódó és egymással ütközô egykristályok kölcsönhatása során létrejövô habszerû szemcsehatár-hálózat jellemez. Ez a mikroszerkezet a legtöbb anyagtudós jó ismerôse, minthogy gyakori jelenség az öntéssel létrehozott kristályos anyagokban. b) Polikristályos növekedési alakzatok, melyeknél új, eltérô kristálytani orientációjú szemcsék képzôdnek a megszilárdulási fronton. Az 1. ábra a polikristályos szerzetek morfológiai gazdagságát illusztrálja. Az egymással versengô nukleációval és növekedéssel létrejövô habszerû szemcsehatár-hálózat az 1.a ábrán látható. Polikristályos dendrites mintázat figyelhetô meg az 1.b ábrán, mely elegendôen hosszú idô után az 1.a ábrán látható alakzathoz hasonlóvá válhat. Polikristályos növekedési formák láthatók az 1.c1.i ábrákon. A közelmúltban végzett kísérletek szerint kristályos szemcsék hozzáadásával az egykristály dendrites megszilárdulási forma polikristályos szédelgô dendritté alakítható (1.c ábra). Jellegzetes polikristályos növekedési mintázat a mûanyag bevásárlószatyrok anyagában is megtalálható szferolit (1.d ábra). Ez az alakzat az anyagok meglehetôsen széles körében figyelhetô meg, többek között elemi szelénben (Se), noduláris öntöttvasban és különféle ásványokban is. Egyes esetekben a szferolitok képzôdése a két végén szétterülô kristálykévék (1.e GRÁNÁSY LÁSZLÓ, PUSZTAI TAMÁS, BÖRZSÖNYI TAMÁS: A POLIKRISTÁLYOS MEGSZILÁRDULÁS TÉRELMÉLETI MODELLEZÉSE 23
A NAPSUGÁRZÁS SPEKTRUMA ÉS AZ EMBERI SZEM ÉRZÉKENYSÉGE
 A NAPSUGÁRZÁS SPEKTRUMA ÉS AZ EMBERI SZEM ÉRZÉKENYSÉGE Antal Ákos BME, Finommechanikai, Optikai Tanszék Kály-Kullai Kristóf, Farkas Henrik BME Kémiai Fizika Tanszék Aki tanulta fizikából a fekete test
A NAPSUGÁRZÁS SPEKTRUMA ÉS AZ EMBERI SZEM ÉRZÉKENYSÉGE Antal Ákos BME, Finommechanikai, Optikai Tanszék Kály-Kullai Kristóf, Farkas Henrik BME Kémiai Fizika Tanszék Aki tanulta fizikából a fekete test
Fénytechnika. A szem, a látás és a színes látás. Dr. Wenzel Klára. egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem
 Fénytechnika A szem, a látás és a színes látás Dr. Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2013 Mi a szín? (MSz 9620) Fizika: a szín meghatározott hullámhosszúságú
Fénytechnika A szem, a látás és a színes látás Dr. Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2013 Mi a szín? (MSz 9620) Fizika: a szín meghatározott hullámhosszúságú
A Planck-eloszlásokról és a fényforrások ekvivalens színhőmérséklet -eiről Erbeszkorn Lajos
 A Planck-eloszlásokról és a fényforrások ekvivalens színhőmérséklet -eiről Erbeszkorn Lajos VTT Szeminárium, Budapest, 2017-10-10 Bevezetés Néhány szó a fényről A fényforrások csoportosítása Az emberi
A Planck-eloszlásokról és a fényforrások ekvivalens színhőmérséklet -eiről Erbeszkorn Lajos VTT Szeminárium, Budapest, 2017-10-10 Bevezetés Néhány szó a fényről A fényforrások csoportosítása Az emberi
OPTIKA. Fénykibocsátás mechanizmusa fényforrás típusok. Dr. Seres István
 OPTIKA Fénykibocsátás mechanizmusa Dr. Seres István Bohr modell Niels Bohr (19) Rutherford felfedezte az atommagot, és igazolta, hogy negatív töltésű elektronok keringenek körülötte. Niels Bohr Bohr ezt
OPTIKA Fénykibocsátás mechanizmusa Dr. Seres István Bohr modell Niels Bohr (19) Rutherford felfedezte az atommagot, és igazolta, hogy negatív töltésű elektronok keringenek körülötte. Niels Bohr Bohr ezt
Alapfogalmak folytatás
 Alapfogalmak folytatás Színek Szem Számítási eljárások Fényforrások 2014.10.14. OMKTI 1 Ismétlés Alapok: Mi a fény? A gyakorlati világítás technika alap mennyisége? Φ K m 0 Φ e ( ) V ( ) d; lm Fényáram,
Alapfogalmak folytatás Színek Szem Számítási eljárások Fényforrások 2014.10.14. OMKTI 1 Ismétlés Alapok: Mi a fény? A gyakorlati világítás technika alap mennyisége? Φ K m 0 Φ e ( ) V ( ) d; lm Fényáram,
A kvantummechanika kísérleti előzményei A részecske hullám kettősségről
 A kvantummechanika kísérleti előzményei A részecske hullám kettősségről Utolsó módosítás: 2016. május 4. 1 Előzmények Franck-Hertz-kísérlet (1) A Franck-Hertz-kísérlet vázlatos elrendezése: http://hyperphysics.phy-astr.gsu.edu/hbase/frhz.html
A kvantummechanika kísérleti előzményei A részecske hullám kettősségről Utolsó módosítás: 2016. május 4. 1 Előzmények Franck-Hertz-kísérlet (1) A Franck-Hertz-kísérlet vázlatos elrendezése: http://hyperphysics.phy-astr.gsu.edu/hbase/frhz.html
Szilárd testek sugárzása
 A fény keletkezése Szilárd testek sugárzása A szilárd test melegítés hatására fényt bocsát ki A sugárzás forrása a közelítőleg termikus egyensúlyban lévő kibocsátó test atomi részecskéinek véletlenszerű
A fény keletkezése Szilárd testek sugárzása A szilárd test melegítés hatására fényt bocsát ki A sugárzás forrása a közelítőleg termikus egyensúlyban lévő kibocsátó test atomi részecskéinek véletlenszerű
Sugárzásos hőtranszport
 Sugárzásos hőtranszport Minden test bocsát ki sugárzást. Ennek hullámhossz szerinti megoszlása a felület hőmérsékletétől függ (spektrum, spektrális eloszlás). Jelen esetben kérdés a Nap és a földi felszínek
Sugárzásos hőtranszport Minden test bocsát ki sugárzást. Ennek hullámhossz szerinti megoszlása a felület hőmérsékletétől függ (spektrum, spektrális eloszlás). Jelen esetben kérdés a Nap és a földi felszínek
Alkalmazás a makrókanónikus sokaságra: A fotongáz
 Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
2. Az emberi hallásról
 2. Az emberi hallásról Élettani folyamat. Valamilyen vivőközegben terjedő hanghullámok hatására, az élőlényben szubjektív hangérzet jön létre. A hangérzékelés részben fizikai, részben fiziológiai folyamat.
2. Az emberi hallásról Élettani folyamat. Valamilyen vivőközegben terjedő hanghullámok hatására, az élőlényben szubjektív hangérzet jön létre. A hangérzékelés részben fizikai, részben fiziológiai folyamat.
A hőmérsékleti sugárzás
 A hőmérsékleti sugárzás Alapfogalmak 1. A hőmérsékleti sugárzás Értelmezés (hőmérsékleti sugárzás): A testek hőmérsékletével kapcsolatos, a teljes elektromágneses spektrumra kiterjedő sugárzást hőmérsékleti
A hőmérsékleti sugárzás Alapfogalmak 1. A hőmérsékleti sugárzás Értelmezés (hőmérsékleti sugárzás): A testek hőmérsékletével kapcsolatos, a teljes elektromágneses spektrumra kiterjedő sugárzást hőmérsékleti
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 5. mérés: Elektronspin rezonancia. 2008. március 18.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Modern Fizika Labor Fizika BSc A mérés dátuma: 28. március 18. A mérés száma és címe: 5. mérés: Elektronspin rezonancia Értékelés: A beadás dátuma: 28. március 26. A mérést végezte: 1/7 A mérés leírása:
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak
 Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 2. Fényhullámok tulajdonságai Cserti József, jegyzet, ELTE, 2007. Az elektromágneses spektrum Látható spektrum (erre állt be a szemünk) UV: ultraibolya
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 2. Fényhullámok tulajdonságai Cserti József, jegyzet, ELTE, 2007. Az elektromágneses spektrum Látható spektrum (erre állt be a szemünk) UV: ultraibolya
A fény mint elektromágneses hullám és mint fényrészecske
 A fény mint elektromágneses hullám és mint fényrészecske Segítség az 5. tétel (Hogyan alkalmazható a hullám-részecske kettősség gondolata a fénysugárzás esetében?) megértéséhez és megtanulásához, továbbá
A fény mint elektromágneses hullám és mint fényrészecske Segítség az 5. tétel (Hogyan alkalmazható a hullám-részecske kettősség gondolata a fénysugárzás esetében?) megértéséhez és megtanulásához, továbbá
Fizikai hangtan, fiziológiai hangtan és építészeti hangtan
 Fizikai hangtan, fiziológiai hangtan és építészeti hangtan Témakörök: A hang terjedési sebessége levegőben Weber Fechner féle pszicho-fizikai törvény Hangintenzitás szint Hangosságszint Álló hullámok és
Fizikai hangtan, fiziológiai hangtan és építészeti hangtan Témakörök: A hang terjedési sebessége levegőben Weber Fechner féle pszicho-fizikai törvény Hangintenzitás szint Hangosságszint Álló hullámok és
1. Az üregsugárzás törvényei
 1. Az üregsugárzás törvényei 1.1. A Wien féle eltolódási törvény és a Stefan-Boltzmann törvény Egy zárt, belül üres fémdoboz kis nyílása az úgynevezett abszolút fekete test. A nyílás elektromágneses sugárzást
1. Az üregsugárzás törvényei 1.1. A Wien féle eltolódási törvény és a Stefan-Boltzmann törvény Egy zárt, belül üres fémdoboz kis nyílása az úgynevezett abszolút fekete test. A nyílás elektromágneses sugárzást
Modern Fizika Labor. 5. ESR (Elektronspin rezonancia) Fizika BSc. A mérés dátuma: okt. 25. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Folyadékszcintillációs spektroszkópia jegyz könyv
 Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Név... intenzitás abszorbancia moláris extinkciós. A Wien-féle eltolódási törvény szerint az abszolút fekete test maximális emisszióképességéhez
 A Név... Válassza ki a helyes mértékegységeket! állandó intenzitás abszorbancia moláris extinkciós A) J s -1 - l mol -1 cm B) W g/cm 3 - C) J s -1 m -2 - l mol -1 cm -1 D) J m -2 cm - A Wien-féle eltolódási
A Név... Válassza ki a helyes mértékegységeket! állandó intenzitás abszorbancia moláris extinkciós A) J s -1 - l mol -1 cm B) W g/cm 3 - C) J s -1 m -2 - l mol -1 cm -1 D) J m -2 cm - A Wien-féle eltolódási
fizikai szemle 2005/6
 fizikai szemle 2005/6 A Magyar Tudományos Akadémia Fizikai Tudományok Osztálya, az Eötvös Loránd Fizikai Társulat, a Magyar Biofizikai Társaság, a Magyar Nukleáris Társaság és az Oktatási Minisztérium
fizikai szemle 2005/6 A Magyar Tudományos Akadémia Fizikai Tudományok Osztálya, az Eötvös Loránd Fizikai Társulat, a Magyar Biofizikai Társaság, a Magyar Nukleáris Társaság és az Oktatási Minisztérium
LÁTÁS FIZIOLÓGIA I.RÉSZ
 LÁTÁS FIZIOLÓGIA I.RÉSZ Dr Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2011 Az 1.rész tartalma: A fény; a fény hatása az élő szervezetre 2. A szem 1. Különböző
LÁTÁS FIZIOLÓGIA I.RÉSZ Dr Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2011 Az 1.rész tartalma: A fény; a fény hatása az élő szervezetre 2. A szem 1. Különböző
Abszorpciós fotometria
 A fény Abszorpciós fotometria Ujfalusi Zoltán PTE ÁOK Biofizikai ntézet 2011. szeptember 15. E B x x Transzverzális hullám A fény elektromos térerősségvektor hullámhossz Az elektromos a mágneses térerősség
A fény Abszorpciós fotometria Ujfalusi Zoltán PTE ÁOK Biofizikai ntézet 2011. szeptember 15. E B x x Transzverzális hullám A fény elektromos térerősségvektor hullámhossz Az elektromos a mágneses térerősség
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Abszorpciós spektroszkópia
 Tartalomjegyzék Abszorpciós spektroszkópia (Nyitrai Miklós; 2011 február 1.) Dolgozat: május 3. 18:00-20:00. Egész éves anyag. Korábbi dolgozatok nem számítanak bele. Felmentés 80% felett. A fény; Elektromágneses
Tartalomjegyzék Abszorpciós spektroszkópia (Nyitrai Miklós; 2011 február 1.) Dolgozat: május 3. 18:00-20:00. Egész éves anyag. Korábbi dolgozatok nem számítanak bele. Felmentés 80% felett. A fény; Elektromágneses
A Markowitz modell: kvadratikus programozás
 A Markowitz modell: kvadratikus programozás Harry Markowitz 1990-ben kapott Közgazdasági Nobel díjat a portfolió optimalizálási modelljéért. Ld. http://en.wikipedia.org/wiki/harry_markowitz Ennek a legegyszer
A Markowitz modell: kvadratikus programozás Harry Markowitz 1990-ben kapott Közgazdasági Nobel díjat a portfolió optimalizálási modelljéért. Ld. http://en.wikipedia.org/wiki/harry_markowitz Ennek a legegyszer
A TERMOKAMERA, AVAGY A CSÖRGŐKÍGYÓ STRATÉGIÁJA
 A TERMOKAMERA, AVAGY A CSÖRGŐKÍGYÓ STRATÉGIÁJA Sokszor használjuk a fényképezés infravörös tartományban kifejezést, ami után rögtön magyarázkodni kényszerülünk, hogy melyik tartományra is gondoltunk. Az
A TERMOKAMERA, AVAGY A CSÖRGŐKÍGYÓ STRATÉGIÁJA Sokszor használjuk a fényképezés infravörös tartományban kifejezést, ami után rögtön magyarázkodni kényszerülünk, hogy melyik tartományra is gondoltunk. Az
11.3. Az Achilles- ín egy olyan rugónak tekinthető, amelynek rugóállandója 3 10 5 N/m. Mekkora erő szükséges az ín 2 mm- rel történő megnyújtásához?
 Fényemisszió 2.45. Az elektromágneses spektrum látható tartománya a 400 és 800 nm- es hullámhosszak között található. Mely energiatartomány (ev- ban) felel meg ennek a hullámhossztartománynak? 2.56. A
Fényemisszió 2.45. Az elektromágneses spektrum látható tartománya a 400 és 800 nm- es hullámhosszak között található. Mely energiatartomány (ev- ban) felel meg ennek a hullámhossztartománynak? 2.56. A
6. Függvények. 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban?
 6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
A hang mint mechanikai hullám
 A hang mint mechanikai hullám I. Célkitűzés Hullámok alapvető jellemzőinek megismerése. A hanghullám fizikai tulajdonságai és a hangérzet közötti összefüggések bemutatása. Fourier-transzformáció alapjainak
A hang mint mechanikai hullám I. Célkitűzés Hullámok alapvető jellemzőinek megismerése. A hanghullám fizikai tulajdonságai és a hangérzet közötti összefüggések bemutatása. Fourier-transzformáció alapjainak
FOTOSZINTETIKUSAN AKTÍV SUGÁRZÁS GLOBÁLSUGÁRZÁS
 FOTOSZINTETIKUSAN AKTÍV SUGÁRZÁS ÉS GLOBÁLSUGÁRZÁS Major György Horváth László, Pintér Krisztina, Nagy Zoltán (Gödöllı) Haszpra László, Barcza Zoltán, Gelybó Györgyi Globálsugárzás: a 0,29 4 mikrométer
FOTOSZINTETIKUSAN AKTÍV SUGÁRZÁS ÉS GLOBÁLSUGÁRZÁS Major György Horváth László, Pintér Krisztina, Nagy Zoltán (Gödöllı) Haszpra László, Barcza Zoltán, Gelybó Györgyi Globálsugárzás: a 0,29 4 mikrométer
Elektromágneses hullámok - Hullámoptika
 Bevezetés a modern fizika fejezeteibe 2. (c) Elektromágneses hullámok - Hullámoptika Utolsó módosítás: 2015. január 17. 1 Az elektromágneses hullámok visszaverődési és törési törvényei (1) Kérdés: Mi történik
Bevezetés a modern fizika fejezeteibe 2. (c) Elektromágneses hullámok - Hullámoptika Utolsó módosítás: 2015. január 17. 1 Az elektromágneses hullámok visszaverődési és törési törvényei (1) Kérdés: Mi történik
11. Egy Y alakú gumikötél egyik ága 20 cm, másik ága 50 cm. A két ág végeit azonos, f = 4 Hz
 Hullámok tesztek 1. Melyik állítás nem igaz a mechanikai hullámok körében? a) Transzverzális hullám esetén a részecskék rezgésének iránya merőleges a hullámterjedés irányára. b) Csak a transzverzális hullám
Hullámok tesztek 1. Melyik állítás nem igaz a mechanikai hullámok körében? a) Transzverzális hullám esetén a részecskék rezgésének iránya merőleges a hullámterjedés irányára. b) Csak a transzverzális hullám
Modern fizika laboratórium
 Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
A gravitáció hatása a hőmérsékleti sugárzásra
 A gravitáció hatása a hőmérsékleti sugárzásra Lendvai József A sugárnyomás a teljes elektromágneses spektrumban ismert jelenség. A kutatás során olyan kísérlet készült, mellyel az alacsony hőmérsékleti
A gravitáció hatása a hőmérsékleti sugárzásra Lendvai József A sugárnyomás a teljes elektromágneses spektrumban ismert jelenség. A kutatás során olyan kísérlet készült, mellyel az alacsony hőmérsékleti
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
VÍZUÁLIS OPTIKA. A színlátás. Dr Wenzel Klára. egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2018
 VÍZUÁLIS OPTIKA A színlátás Dr Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2018 A színlátás Mi a szín? (MSz 9620) Fizika: a szín meghatározott hullámhosszúságú
VÍZUÁLIS OPTIKA A színlátás Dr Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2018 A színlátás Mi a szín? (MSz 9620) Fizika: a szín meghatározott hullámhosszúságú
Tartalomjegyzék. Emlékeztetõ. Emlékeztetõ. Spektroszkópia. Fényelnyelés híg oldatokban A fény; Abszorpciós spektroszkópia
 Tartalomjegyzék PÉCS TUDOMÁNYEGYETEM ÁLTALÁNOS ORVOSTUDOMÁNY KAR A fény; Abszorpciós spektroszkópia Elektromágneses hullám kölcsönhatása anyaggal; (Nyitrai Miklós; 2015 január 27.) Az abszorpció mérése;
Tartalomjegyzék PÉCS TUDOMÁNYEGYETEM ÁLTALÁNOS ORVOSTUDOMÁNY KAR A fény; Abszorpciós spektroszkópia Elektromágneses hullám kölcsönhatása anyaggal; (Nyitrai Miklós; 2015 január 27.) Az abszorpció mérése;
Mézerek és lézerek. Berta Miklós SZE, Fizika és Kémia Tsz. 2006. november 19.
 és lézerek Berta Miklós SZE, Fizika és Kémia Tsz. 2006. november 19. Fény és anyag kölcsönhatása 2 / 19 Fény és anyag kölcsönhatása Fény és anyag kölcsönhatása E 2 (1) (2) (3) E 1 (1) gerjesztés (2) spontán
és lézerek Berta Miklós SZE, Fizika és Kémia Tsz. 2006. november 19. Fény és anyag kölcsönhatása 2 / 19 Fény és anyag kölcsönhatása Fény és anyag kölcsönhatása E 2 (1) (2) (3) E 1 (1) gerjesztés (2) spontán
19. A fényelektromos jelenségek vizsgálata
 19. A fényelektromos jelenségek vizsgálata PÁPICS PÉTER ISTVÁN csillagász, 3. évfolyam Mérőpár: Balázs Miklós 2006.04.19. Beadva: 2006.05.15. Értékelés: A MÉRÉS LEÍRÁSA Fontos megállapítás, hogy a fénysugárzásban
19. A fényelektromos jelenségek vizsgálata PÁPICS PÉTER ISTVÁN csillagász, 3. évfolyam Mérőpár: Balázs Miklós 2006.04.19. Beadva: 2006.05.15. Értékelés: A MÉRÉS LEÍRÁSA Fontos megállapítás, hogy a fénysugárzásban
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Modern Fizika Labor. 11. Spektroszkópia. Fizika BSc. A mérés dátuma: dec. 16. A mérés száma és címe: Értékelés: A beadás dátuma: dec. 21.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Tartalomjegyzék. Emlékeztetõ. Emlékeztetõ. Spektroszkópia. Fényelnyelés híg oldatokban 4/11/2016. A fény; Abszorpciós spektroszkópia
 Tartalomjegyzék PÉCS TUDOMÁNYEGYETEM ÁLTALÁNOS ORVOSTUDOMÁNY KAR A fény; Abszorpciós spektroszkópia Elektromágneses hullám kölcsönhatása anyaggal; (Nyitrai Miklós; 2016 március 1.) Az abszorpció mérése;
Tartalomjegyzék PÉCS TUDOMÁNYEGYETEM ÁLTALÁNOS ORVOSTUDOMÁNY KAR A fény; Abszorpciós spektroszkópia Elektromágneses hullám kölcsönhatása anyaggal; (Nyitrai Miklós; 2016 március 1.) Az abszorpció mérése;
Milyen színűek a csillagok?
 Milyen színűek a csillagok? A fényesebb csillagok színét szabad szemmel is jól láthatjuk. Az egyik vörös, a másik kék, de vannak fehéren villódzók, sárga, narancssárga színűek is. Vajon mi lehet az eltérő
Milyen színűek a csillagok? A fényesebb csillagok színét szabad szemmel is jól láthatjuk. Az egyik vörös, a másik kék, de vannak fehéren villódzók, sárga, narancssárga színűek is. Vajon mi lehet az eltérő
Hullámok, hanghullámok
 Hullámok, hanghullámok Hullámokra jellemző mennyiségek: Amplitúdó: a legnagyobb, maximális kitérés nagysága jele: A, mértékegysége: m (egyéb mértékegységek: dm, cm, mm, ) Hullámhossz: két azonos rezgési
Hullámok, hanghullámok Hullámokra jellemző mennyiségek: Amplitúdó: a legnagyobb, maximális kitérés nagysága jele: A, mértékegysége: m (egyéb mértékegységek: dm, cm, mm, ) Hullámhossz: két azonos rezgési
Az Ampère-Maxwell-féle gerjesztési törvény
 Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. február 23. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2009. március 2. A mérést végezte: Zsigmond Anna Márton Krisztina
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. február 23. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2009. március 2. A mérést végezte: Zsigmond Anna Márton Krisztina
OPTIKA. Fotometria. Dr. Seres István
 OPTIKA Dr. Seres István Segédmennyiségek: Síkszög: ívhossz/sugár i r Kör középponti szöge: 2 (radián) Térszög: terület/sugár a négyzeten A sr (szteradián = sr) 2 r Gömb középponti térszöge: 4 (szteradián)
OPTIKA Dr. Seres István Segédmennyiségek: Síkszög: ívhossz/sugár i r Kör középponti szöge: 2 (radián) Térszög: terület/sugár a négyzeten A sr (szteradián = sr) 2 r Gömb középponti térszöge: 4 (szteradián)
Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai 1.
 Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai.). Feladat. Határozzuk meg az alábbi integrálokat: a) x x + dx d) xe x dx b) c)
Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai.). Feladat. Határozzuk meg az alábbi integrálokat: a) x x + dx d) xe x dx b) c)
OPTIKA. Fotometria. Dr. Seres István
 OPTIKA Dr. Seres István Segédmennyiségek: Síkszög: ívhossz/sugár Kör középponti szöge: 2 (radián) Térszög: terület/sugár a négyzeten sr A 2 r (szteradián = sr) i r Gömb középponti térszöge: 4 (szteradián)
OPTIKA Dr. Seres István Segédmennyiségek: Síkszög: ívhossz/sugár Kör középponti szöge: 2 (radián) Térszög: terület/sugár a négyzeten sr A 2 r (szteradián = sr) i r Gömb középponti térszöge: 4 (szteradián)
A napenergia alapjai
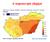 A napenergia alapjai Magyarország energia mérlege sötét Ahonnan származik Forrás: Kardos labor 3 A légkör felső határára és a Föld felszínére érkező sugárzás spektruma Nem csak az a spektrum tud energiát
A napenergia alapjai Magyarország energia mérlege sötét Ahonnan származik Forrás: Kardos labor 3 A légkör felső határára és a Föld felszínére érkező sugárzás spektruma Nem csak az a spektrum tud energiát
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
A Hisztogram használata a digitális képszerkesztésben
 Mechatronika, Optika és Mûszertechnika Tanszék A Hisztogram használata a digitális képszerkesztésben Tárgy: Fotó és Készítette: Curávy Tamás képszerkesztési technikák B1Y6IV Elõadó: Antal Á kos Budapest,
Mechatronika, Optika és Mûszertechnika Tanszék A Hisztogram használata a digitális képszerkesztésben Tárgy: Fotó és Készítette: Curávy Tamás képszerkesztési technikák B1Y6IV Elõadó: Antal Á kos Budapest,
A Markowitz modell: kvadratikus programozás
 A Markowitz modell: kvadratikus programozás Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2011/12 tanév, II. félév Losonczi László (DE) A Markowitz modell 2011/12 tanév,
A Markowitz modell: kvadratikus programozás Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2011/12 tanév, II. félév Losonczi László (DE) A Markowitz modell 2011/12 tanév,
Orvosi Biofizika I. 12. vizsgatétel. IsmétlésI. -Fény
 Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
A magyar teljesítménytúra-naptár fejlődése,
 A magyar teljesítménytúra-naptár fejlődése, 28-216 Tartalomjegyzék Ferenci Tamás, tamas.ferenci@medstat.hu 217. február 2. Cél 1 Számítástechnikai megjegyzések 1 Eredmények 2 Túrák és túrázok száma..........................................
A magyar teljesítménytúra-naptár fejlődése, 28-216 Tartalomjegyzék Ferenci Tamás, tamas.ferenci@medstat.hu 217. február 2. Cél 1 Számítástechnikai megjegyzések 1 Eredmények 2 Túrák és túrázok száma..........................................
Atomfizika. Fizika kurzus Dr. Seres István
 Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés J.J. Thomson (1897) Katódsugárcsővel végzett kísérleteket az elektron fajlagos töltésének (e/m) meghatározására. A katódsugarat alkotó részecskét
Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés J.J. Thomson (1897) Katódsugárcsővel végzett kísérleteket az elektron fajlagos töltésének (e/m) meghatározására. A katódsugarat alkotó részecskét
A 2017/2018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ. Pohár rezonanciája
 Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Hullámok tesztek. 3. Melyik állítás nem igaz a mechanikai hullámok körében?
 Hullámok tesztek 1. Melyik állítás nem igaz a mechanikai hullámok körében? a) Transzverzális hullám esetén a részecskék rezgésének iránya merıleges a hullámterjedés irányára. b) Csak a transzverzális hullám
Hullámok tesztek 1. Melyik állítás nem igaz a mechanikai hullámok körében? a) Transzverzális hullám esetén a részecskék rezgésének iránya merıleges a hullámterjedés irányára. b) Csak a transzverzális hullám
Távérzékelés, a jöv ígéretes eszköze
 Távérzékelés, a jöv ígéretes eszköze Ritvayné Szomolányi Mária Frombach Gabriella VITUKI CONSULT Zrt. A távérzékelés segítségével: különböz6 magasságból, tetsz6leges id6ben és a kívánt hullámhossz tartományokban
Távérzékelés, a jöv ígéretes eszköze Ritvayné Szomolányi Mária Frombach Gabriella VITUKI CONSULT Zrt. A távérzékelés segítségével: különböz6 magasságból, tetsz6leges id6ben és a kívánt hullámhossz tartományokban
Transzformátor rezgés mérés. A BME Villamos Energetika Tanszéken
 Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Dr. Nagy Balázs Vince D428
 Műszaki Optika 2. előadás Dr. Nagy Balázs Vince D428 nagyb@mogi.bme.hu Izzólámpa és fénycső 30,0 25,0 20,0 15,0 10,0 5,0 0,0 350 400 450 500 550 600 650 700 750 2 Fényforrások csoportosítása Fényforrások
Műszaki Optika 2. előadás Dr. Nagy Balázs Vince D428 nagyb@mogi.bme.hu Izzólámpa és fénycső 30,0 25,0 20,0 15,0 10,0 5,0 0,0 350 400 450 500 550 600 650 700 750 2 Fényforrások csoportosítása Fényforrások
Hőmérsékleti sugárzás
 Ideális fekete test sugárzása Hőmérsékleti sugárzás Elméleti háttér Egy ideális fekete test leírható egy egyenletes hőmérsékletű falú üreggel. A fala nemcsak kibocsát, hanem el is nyel energiát, és spektrális
Ideális fekete test sugárzása Hőmérsékleti sugárzás Elméleti háttér Egy ideális fekete test leírható egy egyenletes hőmérsékletű falú üreggel. A fala nemcsak kibocsát, hanem el is nyel energiát, és spektrális
Abszorpciós fotometria
 abszorpció Abszorpciós fotometria Spektroszkópia - Színképvizsgálat Spektro-: görög; jelente kép/szín -szkópia: görög; néz/látás/vizsgálat Ujfalusi Zoltán PTE ÁOK Biofizikai Intézet 2012. február Vizsgálatok
abszorpció Abszorpciós fotometria Spektroszkópia - Színképvizsgálat Spektro-: görög; jelente kép/szín -szkópia: görög; néz/látás/vizsgálat Ujfalusi Zoltán PTE ÁOK Biofizikai Intézet 2012. február Vizsgálatok
Mechanikai hullámok. Hullámhegyek és hullámvölgyek alakulnak ki.
 Mechanikai hullámok Mechanikai hullámnak nevezzük, ha egy anyagban az anyag részecskéinek rezgésállapota továbbterjed. A mechanikai hullám terjedéséhez tehát szükség van valamilyen anyagra (légüres térben
Mechanikai hullámok Mechanikai hullámnak nevezzük, ha egy anyagban az anyag részecskéinek rezgésállapota továbbterjed. A mechanikai hullám terjedéséhez tehát szükség van valamilyen anyagra (légüres térben
u,v chromaticity diagram
 u,v chromaticity diagram CIE 1976 a,b colour difference and CIELAB components Colour difference: E ab (L*) 2 + (a*) 2 + (b*) 2 1/2 CIE1976 a,b chroma: C ab * (a* 2 + b* 2 ) 1/2 CIE 1976 a,b hue-angle:
u,v chromaticity diagram CIE 1976 a,b colour difference and CIELAB components Colour difference: E ab (L*) 2 + (a*) 2 + (b*) 2 1/2 CIE1976 a,b chroma: C ab * (a* 2 + b* 2 ) 1/2 CIE 1976 a,b hue-angle:
Színek 2013.10.20. 1
 Színek 2013.10.20. 1 Képek osztályozása Álló vagy mozgó (animált) kép Fekete-fehér vagy színes kép 2013.10.20. 2 A színes kép Az emberi szem kb. 380-760 nm hullámhosszúságú fénytartományra érzékeny. (Ez
Színek 2013.10.20. 1 Képek osztályozása Álló vagy mozgó (animált) kép Fekete-fehér vagy színes kép 2013.10.20. 2 A színes kép Az emberi szem kb. 380-760 nm hullámhosszúságú fénytartományra érzékeny. (Ez
Bevezetés a modern fizika fejezeteibe. 4. (a) Kvantummechanika. Utolsó módosítás: november 15. Dr. Márkus Ferenc BME Fizika Tanszék
 Bevezetés a modern fizika fejezeteibe 4. (a) Kvantummechanika Utolsó módosítás: 2015. november 15. 1 Előzmények Az atomok színképe (1) A fehér fény komponensekre bontható: http://en.wikipedia.org/wiki/spectrum
Bevezetés a modern fizika fejezeteibe 4. (a) Kvantummechanika Utolsó módosítás: 2015. november 15. 1 Előzmények Az atomok színképe (1) A fehér fény komponensekre bontható: http://en.wikipedia.org/wiki/spectrum
Abszorpciós spektrumvonalak alakja. Vonalak eredete (ld. előző óra)
 Abszorpciós spektrumvonalak alakja Vonalak eredete (ld. előző óra) Nagysága Kiszélesedése Elem mennyiségének becslése a vonalerősségből Elemi statfiz Boltzmann-faktor: Megadja egy állapot súlyát a sokaságban
Abszorpciós spektrumvonalak alakja Vonalak eredete (ld. előző óra) Nagysága Kiszélesedése Elem mennyiségének becslése a vonalerősségből Elemi statfiz Boltzmann-faktor: Megadja egy állapot súlyát a sokaságban
A légköri sugárzás. Sugárzási törvények, légköri veszteségek, energiaháztartás
 A légköri sugárzás Sugárzási törvények, légköri veszteségek, energiaháztartás Sugárzási törvények I. 0. Minden T>0 K hőmérsékletű test sugároz 1. Planck törvény: minden testre megadható egy hőmérséklettől
A légköri sugárzás Sugárzási törvények, légköri veszteségek, energiaháztartás Sugárzási törvények I. 0. Minden T>0 K hőmérsékletű test sugároz 1. Planck törvény: minden testre megadható egy hőmérséklettől
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Matematika A2 vizsga mgeoldása június 4.
 Matematika A vizsga mgeoldása 03. június.. (a (3 pont Definiálja az f(x, y függvény határértékét az (x 0, y 0 helyen! Megoldás: Legyen D R, f : D R. Legyen az f(x, y függvény értelmezve az (x 0, y 0 pont
Matematika A vizsga mgeoldása 03. június.. (a (3 pont Definiálja az f(x, y függvény határértékét az (x 0, y 0 helyen! Megoldás: Legyen D R, f : D R. Legyen az f(x, y függvény értelmezve az (x 0, y 0 pont
Műszeres analitika II. (TKBE0532)
 Műszeres analitika II. (TKBE0532) 4. előadás Spektroszkópia alapjai Dr. Andrási Melinda Debreceni Egyetem Természettudományi és Technológiai Kar Szervetlen és Analitikai Kémiai Tanszék A fény elektromágneses
Műszeres analitika II. (TKBE0532) 4. előadás Spektroszkópia alapjai Dr. Andrási Melinda Debreceni Egyetem Természettudományi és Technológiai Kar Szervetlen és Analitikai Kémiai Tanszék A fény elektromágneses
Compton-effektus. Zsigmond Anna. jegyzıkönyv. Fizika BSc III.
 Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Gépi tanulás és Mintafelismerés
 Gépi tanulás és Mintafelismerés jegyzet Csató Lehel Matematika-Informatika Tanszék BabesBolyai Tudományegyetem, Kolozsvár 2007 Aug. 20 2 1. fejezet Bevezet A mesterséges intelligencia azon módszereit,
Gépi tanulás és Mintafelismerés jegyzet Csató Lehel Matematika-Informatika Tanszék BabesBolyai Tudományegyetem, Kolozsvár 2007 Aug. 20 2 1. fejezet Bevezet A mesterséges intelligencia azon módszereit,
A SZÍNEKRŐL III. RÉSZ A CIE színrendszer
 A SZÍNEKRŐL III. RÉSZ A CIE színrendszer Dr Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2011 A CIE színinger mérő rendszer (1931) Commission Internationale
A SZÍNEKRŐL III. RÉSZ A CIE színrendszer Dr Wenzel Klára egyetemi magántanár Budapesti Műszaki és Gazdaságtudományi Egyetem Budapest, 2011 A CIE színinger mérő rendszer (1931) Commission Internationale
Geometriai és hullámoptika. Utolsó módosítás: május 10..
 Geometriai és hullámoptika Utolsó módosítás: 2016. május 10.. 1 Mi a fény? Részecske vagy hullám? Isaac Newton (1642-1727) Pierre de Fermat (1601-1665) Christiaan Huygens (1629-1695) Thomas Young (1773-1829)
Geometriai és hullámoptika Utolsó módosítás: 2016. május 10.. 1 Mi a fény? Részecske vagy hullám? Isaac Newton (1642-1727) Pierre de Fermat (1601-1665) Christiaan Huygens (1629-1695) Thomas Young (1773-1829)
Sugárzáson, és infravörös sugárzáson alapuló hőmérséklet mérés.
 Sugárzáson, és infravörös sugárzáson alapuló hőmérséklet mérés. A sugárzáson alapuló hőmérsékletmérés (termográfia),azt a fizikai jelenséget használja fel, hogy az abszolút nulla K hőmérséklet (273,16
Sugárzáson, és infravörös sugárzáson alapuló hőmérséklet mérés. A sugárzáson alapuló hőmérsékletmérés (termográfia),azt a fizikai jelenséget használja fel, hogy az abszolút nulla K hőmérséklet (273,16
3. Lineáris differenciálegyenletek
 3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
Mechanika I-II. Példatár
 Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Abszorpció, emlékeztetõ
 Hogyan készültek ezek a képek? PÉCI TUDMÁNYEGYETEM ÁLTALÁN RVTUDMÁNYI KAR Fluoreszcencia spektroszkópia (Nyitrai Miklós; február.) Lumineszcencia - elemi lépések Abszorpció, emlékeztetõ Energia elnyelése
Hogyan készültek ezek a képek? PÉCI TUDMÁNYEGYETEM ÁLTALÁN RVTUDMÁNYI KAR Fluoreszcencia spektroszkópia (Nyitrai Miklós; február.) Lumineszcencia - elemi lépések Abszorpció, emlékeztetõ Energia elnyelése
Intelligens Rendszerek Elmélete. Biológiai érzékelők és tanulságok a technikai adaptáláshoz. Az érzékelés alapfogalmai
 Intelligens Rendszerek Elmélete dr. Kutor László Biológiai érzékelők és tanulságok a technikai adaptáláshoz http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 2/1 Az érzékelés
Intelligens Rendszerek Elmélete dr. Kutor László Biológiai érzékelők és tanulságok a technikai adaptáláshoz http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 2/1 Az érzékelés
Exponenciális, logaritmikus függvények
 Exponenciális, logaritmikus függvények DEFINÍCIÓ: (Összetett függvény) Ha az értékkészlet elemeihez, mint értelmezési tartományhoz egy újabb egyértelmű hozzárendelést adunk meg, akkor összetett (közvetett)
Exponenciális, logaritmikus függvények DEFINÍCIÓ: (Összetett függvény) Ha az értékkészlet elemeihez, mint értelmezési tartományhoz egy újabb egyértelmű hozzárendelést adunk meg, akkor összetett (közvetett)
2. REZGÉSEK Harmonikus rezgések: 2.2. Csillapított rezgések
 . REZGÉSEK.1. Harmonikus rezgések: Harmonikus erő: F = D x D m ẍ= D x (ezt a mechanikai rendszert lineáris harmonikus oszcillátornak nevezik) (Oszcillátor körfrekvenciája) ẍ x= Másodrendű konstansegyütthatós
. REZGÉSEK.1. Harmonikus rezgések: Harmonikus erő: F = D x D m ẍ= D x (ezt a mechanikai rendszert lineáris harmonikus oszcillátornak nevezik) (Oszcillátor körfrekvenciája) ẍ x= Másodrendű konstansegyütthatós
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Optika gyakorlat 6. Interferencia. I = u 2 = u 1 + u I 2 cos( Φ)
 Optika gyakorlat 6. Interferencia Interferencia Az interferencia az a jelenség, amikor kett vagy több hullám fázishelyes szuperpozíciója révén a térben állóhullám kép alakul ki. Ez elektromágneses hullámok
Optika gyakorlat 6. Interferencia Interferencia Az interferencia az a jelenség, amikor kett vagy több hullám fázishelyes szuperpozíciója révén a térben állóhullám kép alakul ki. Ez elektromágneses hullámok
A távérzékelés és fizikai alapjai 3. Fizikai alapok
 A távérzékelés és fizikai alapjai 3. Fizikai alapok Csornai Gábor László István Budapest Főváros Kormányhivatala Mezőgazdasági Távérzékelési és Helyszíni Ellenőrzési Osztály Az előadás 2011-es átdolgozott
A távérzékelés és fizikai alapjai 3. Fizikai alapok Csornai Gábor László István Budapest Főváros Kormányhivatala Mezőgazdasági Távérzékelési és Helyszíni Ellenőrzési Osztály Az előadás 2011-es átdolgozott
Látás. Látás. A környezet érzékelése a látható fény segítségével. A szem a fényérzékelés speciális, páros szerve (érzékszerv).
 Látás A szem felépítése és működése. Optikai leképezés a szemben, akkomodáció. Képalkotási hibák. A fotoreceptorok tulajdonságai és működése. A szem felbontóképessége. A színlátás folyamata. 2014/11/18
Látás A szem felépítése és működése. Optikai leképezés a szemben, akkomodáció. Képalkotási hibák. A fotoreceptorok tulajdonságai és működése. A szem felbontóképessége. A színlátás folyamata. 2014/11/18
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
Least Squares becslés
 Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
DIFFERENCIÁLEGYENLETEK. BSc. Matematika II. BGRMA2HNND, BGRMA2HNNC
 BSC MATEMATIKA II. MÁSODRENDŰ LINEÁRIS DIFFERENCIÁLEGYENLETEK BSc. Matematika II. BGRMAHNND, BGRMAHNNC MÁSODRENDŰ DIFFERENCIÁLEGYENLETEK Egy explicit közönséges másodrendű differenciálegyenlet általános
BSC MATEMATIKA II. MÁSODRENDŰ LINEÁRIS DIFFERENCIÁLEGYENLETEK BSc. Matematika II. BGRMAHNND, BGRMAHNNC MÁSODRENDŰ DIFFERENCIÁLEGYENLETEK Egy explicit közönséges másodrendű differenciálegyenlet általános
Matematikai alapok és valószínőségszámítás. Valószínőségi eloszlások Binomiális eloszlás
 Matematikai alapok és valószínőségszámítás Valószínőségi eloszlások Binomiális eloszlás Bevezetés A tudományos életben megfigyeléseket teszünk, kísérleteket végzünk. Ezek többféle különbözı eredményre
Matematikai alapok és valószínőségszámítás Valószínőségi eloszlások Binomiális eloszlás Bevezetés A tudományos életben megfigyeléseket teszünk, kísérleteket végzünk. Ezek többféle különbözı eredményre
1. A hang, mint akusztikus jel
 1. A hang, mint akusztikus jel Mechanikai rezgés - csak anyagi közegben terjed. A levegő molekuláinak a hangforrástól kiinduló, egyre csillapodva tovaterjedő mechanikai rezgése. Nemcsak levegőben, hanem
1. A hang, mint akusztikus jel Mechanikai rezgés - csak anyagi közegben terjed. A levegő molekuláinak a hangforrástól kiinduló, egyre csillapodva tovaterjedő mechanikai rezgése. Nemcsak levegőben, hanem
Modern Fizika Labor. 12. Infravörös spektroszkópia. Fizika BSc. A mérés dátuma: okt. 04. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
A fény keletkezése. Hőmérsékleti sugárzás. Hőmérsékleti sugárzás. Lumineszcencia. Lézer. Tapasztalat: a forró testek Hőmérsékleti sugárzás
 A fény keletkezése Hőmérsékleti sugárzás Hőmérsékleti sugárzás Lumineszcencia Lézer Tapasztalat: a forró testek Hőmérsékleti sugárzás Környezetének hőfokától függetlenül minden test minden, abszolút nulla
A fény keletkezése Hőmérsékleti sugárzás Hőmérsékleti sugárzás Lumineszcencia Lézer Tapasztalat: a forró testek Hőmérsékleti sugárzás Környezetének hőfokától függetlenül minden test minden, abszolút nulla
Speciális relativitás
 Fizika 1 előadás 2016. április 6. Speciális relativitás Relativisztikus kinematika Utolsó módosítás: 2016. április 4.. 1 Egy érdekesség: Fizeau-kísérlet A v sebességgel áramló n törésmutatójú folyadékban
Fizika 1 előadás 2016. április 6. Speciális relativitás Relativisztikus kinematika Utolsó módosítás: 2016. április 4.. 1 Egy érdekesség: Fizeau-kísérlet A v sebességgel áramló n törésmutatójú folyadékban
HULLADÉKCSÖKKENTÉS. EEA Grants Norway Grants. Élelmiszeripari zöld innovációs program megvalósítása. Dr. Nagy Attila, Debreceni Egyetem 2014.10.28.
 Élelmiszeripari zöld innovációs program megvalósítása EEA Grants Norway Grants HULLADÉKCSÖKKENTÉS Dr. Nagy Attila, Debreceni Egyetem HU09-0015-A1-2013 1 Beruházás oka A vágóhidakról kikerülő baromfi nyesedék
Élelmiszeripari zöld innovációs program megvalósítása EEA Grants Norway Grants HULLADÉKCSÖKKENTÉS Dr. Nagy Attila, Debreceni Egyetem HU09-0015-A1-2013 1 Beruházás oka A vágóhidakról kikerülő baromfi nyesedék
Zaj- és rezgés. Törvényszerűségek
 Zaj- és rezgés Törvényszerűségek A hang valamilyen közegben létrejövő rezgés. A vivőközeg szerint megkülönböztetünk: léghangot (a vivőközeg gáz, leggyakrabban levegő); folyadékhangot (a vivőközeg folyadék,
Zaj- és rezgés Törvényszerűségek A hang valamilyen közegben létrejövő rezgés. A vivőközeg szerint megkülönböztetünk: léghangot (a vivőközeg gáz, leggyakrabban levegő); folyadékhangot (a vivőközeg folyadék,
Optika. Kedd 16:00 Eötvös-terem
 Fizika és csillagászat tagozatok. Kedd 16:00 Eötvös-terem 1. Balogh Renáta (SZTE TTK) 2. Börzsönyi Ádám (SZTE TTK) 3. Fekete Júlia (ELTE TTK) 4. Kákonyi Róbert (SZTE TTK) 5. Major Csaba Ferenc (SZTE TTK)
Fizika és csillagászat tagozatok. Kedd 16:00 Eötvös-terem 1. Balogh Renáta (SZTE TTK) 2. Börzsönyi Ádám (SZTE TTK) 3. Fekete Júlia (ELTE TTK) 4. Kákonyi Róbert (SZTE TTK) 5. Major Csaba Ferenc (SZTE TTK)
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia. 2008. május 6.
 Modern Fizika Labor Fizika BSc A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia Értékelés: A beadás dátuma: 28. május 13. A mérést végezte: 1/5 A mérés célja A mérés célja az
Modern Fizika Labor Fizika BSc A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia Értékelés: A beadás dátuma: 28. május 13. A mérést végezte: 1/5 A mérés célja A mérés célja az
