Kapcsolat idegsejtek között: a szinapszis
|
|
|
- Dezső Török
- 8 évvel ezelőtt
- Látták:
Átírás
1 Moó: Legjobban úgy érjük meg - folyaja a Sruccmadár ha azonnal hozzákezdünk Lewis Carroll, 1865 Kapcsola idegsejek közö: a szinapszis ELTE, nov. 10. Az előadás felhasználja Lengyel Máé és Kiss Tamás korábbi fóliái
2 Szinapszis modellek 1. preszinapikus akciós poenciál 2. Ca 2+ influx 3. ranszmier ürülés a vezikulákból szinapszis modellek célja: a preszinapikus sej üzelései alapján kiszámíani a poszszinapikus poenciálválozás 4. ranszmier-recepor köés 5.poszszinapukus kondukancia ("PSG"), áram (PSC) és poenciálválaozás (PSP) Modellek az idegrendszer-kuaásban - ELTE TTK, 2002 avaszi félév hp:// Lengyel Máé: Egysej modellek II / 1
3 Részlees kineikai szinapszis modellek: a preszinapikus oldal (1-3.) kineikai séma (példa) d Ca 2+ d I Ca Ca 2+ Ca V pre β I Ca Ca 2+ τ Ca 4k b Ca 2+ X 4k u X * Emlékezeõ: I Ca 4Ca 2+ +X ds d k b g Ca s s V pre E Ca X* X*+W k 1 k W* 3 nt k c k 2 k u Ca 2+ inracelluláris kálcium X,X* fehérje, akivál fehérje W,W* vezikula, akivál vezikula T ranszmier s V pre V pre s dx d dx * d dw d dw * d d T d k b Ca 2+ X k b Ca 2+ X k 1 X * k 1 X * k 1 X * k 3 n W * W W W k u X * k u X * k 2 W * k 2 W * k 2 W * k c T k 3 W * [Ca 2+ ] X*, W* [T] Modellek az idegrendszer-kuaásban - ELTE TTK, 2002 avaszi félév hp:// Lengyel Máé: Egysej modellek II / 2
4 Részlees kineikai szinapszis modellek: a poszszinapikus oldal (4-5.) C m V posz g sziv E sziv... g syn E syn T C 0 r b [T] r u1 kineikai séma (példa) r b [T] r o C 1 C 2 O (q) r u2 r c r d r r r d r r Emlékezeõ: I syn g syn q E syn V posz T C D O D 1 D 2 ranszmier zár recepor deszenziizál recepor nyio recepor preszinapikus oldal Egyszerûsíe kineikai szinapszis modellek poszszinapikus oldal T V pre 1 e T max V pre K V dq d C (1-q) T 1 α [T] β q O (q) q Modellek az idegrendszer-kuaásban - ELTE TTK, 2002 avaszi félév hp:// Lengyel Máé: Egysej modellek II / 3
5 " $ %! # ' & * * *,, ) + -.,, Fenomenológikus szinapszis modellek egyelen preszinapikus akciós poenciál álal okozo poszszinapikus kondukancia válozás V posz I syn g syn E syn # V posz 0 V pre 0 # V q 0 d 0 az egyedi poszszinapikus kondukancia válozások lineáris összegzése (konvolúció Dirac-delával) C m g sziv E sziv... g syn E syn 1 alfa-függvény q ( p e 1 p 1 dupla exponenciális-függvény τ 1 =10, τ 2 =200 q de A 1, 2 e 2 e p =50 idõ [msec] p =100 p = τ 1 =10, τ 2 = idõ [msec] τ 1 =50, τ 2 = Modellek az idegrendszer-kuaásban - ELTE TTK, 2002 avaszi félév hp:// Lengyel Máé: Egysej modellek II / 4
6 Szinapszis modellek: összefoglaló kineikai modellek részlees egyszerûsíe fenomenológikus modellek válozók száma preszinapikus >=5 0 reprodukál jelenségek poszszinapikus ~5 1 szenziizáció igen nem nem deszenziizáció igen nem nem elíõdés (PSG, PSC) igen nem nem elíõdés (PSP) igen igen nem 0 Serkenés vagy gálás? serkenés V küszöb sönölõ gálás! V nyug E syn addiív haás divizív haás V pre /mv [T]/mM q V posz /mv V posz /mv q α gálás szubrakív haás [msec] [msec] Modellek az idegrendszer-kuaásban - ELTE TTK, 2003 avaszi félév hp:// Lengyel Máé: Egysej modellek III / 14
7 Tanulás
8 Hálózaok álalános leírása készinű dinamika Álalánosságban valamely neuronhálózao irányío, színeze és cimkéze gráffal reprezenálhaunk. A neuronhálóza működésé készinű dinamikával szokás jellemezni: da() = f(a, S, ) a sejek akiviására (a = akiviás vekor) d ds() = F (a, S) a szinapszisok haékonyságára (S = szinapikus haékonyság márix) d
9 Tanulási paradigmák Munkahipoézis : a anulás agyi folyamaának alapja a szinapszisok időbeli módosulása Felügyele nélküli anulás (unsupervised learning) Nem ismerjuk a bemenő jeleke, a hálózaól az várjuk, hogy sruurálja azoka. Példák: Hebb-szabály, módosío Hebb-szabályok, kovariancia szabály, BCM szabály, szinapikus plasziciás, LTP/LTD Felügyel anulás (supervised learning) A hálózao úgy anjuk, hogy ismerjük a bemenő jeleke és elvárjuk a megfelelő válasz. A hálózanak minden lépésben megmondjuk a hibá. A anulási szabály explicie aralmazza a hibá, ami minden lépésben a aníó ad meg. Megerősíéses anulás (reinforcemen learning) A hálózao úgy aníjuk, hogy ismerjük a bemenő jeleke, és elvárjuk a jó válasz, azonban a hálózanak csak az mondjuk meg, a válasza helyes vol, vagy sem.
10 LTP Long Term Poeniaion Az LTP (a szinapszisok hosszú ávú erősődése) a szinapikus plasziciás egyik fajája Az LTP indukció egy fajájának vázlaa: A, konroll állapoban az impulzus álal kiválo válasz. B, erős ingerlés haására posz-szinapikus üzelés alakul ki. C, a később alkalmazo esz impulzussal erősebb válasz mérheő Az ábrák mos és a kövekező oldalakon Gersner és Kisler Spiking Neuron Models. Single Neurons, Populaions, Plasiciy (Cambridge Universiy Press, 2002) c. könyvéből származnak. Online: hp://diwww.epfl.ch/~gersner/spnm/
11 A Hebb szabály I. When an axon of cell A is near enough o excie cell B, and repeaedly or consisenly akes par in firing i, some growh process or meabolic change akes par in one or boh cells such ha A s efficiency, as one of cell firing B, is increased (Donald O. Hebb, The Organizaion of Behavior, Wiley, New York, 1949) Ha egy A sej axonja elég közel van ahhoz, hogy egy B seje serkensen, és isméelen vagy kövekezeesen rész vesz a B sej kisüésében, akkor valamilyen növekedési folyama vagy meaboropikus válozás kövekezében a jövbően az A sej haékonyabban fogja kisüni a B-seje.
12 A Hebb szabály II. A Hebb-ípusú szinapszis haékonysága lokális, inerakív és időzíe folyama során növekszik. Ez részleesebben az jeleni, hogy a szinapszis módosulásában csak a pre és a poszszinapikus sej akiviása jászik szerepe, a szinapikus válozáshoz csak ez a ké sej szükséges, és a ké sej akiviásának időben összehangolnak kell lennie.
13 A Hebb szabály III. A szabály maemaikai megfogalmazása v j... w ij v i w ik v k Az álalános formula a lokaliás és az inerakiviás alapján ilyen alakú: F (w ij (), v i (), v j ()) (ez még NEM a Hebb-szabály!) dw ij () d = (foly. köv...)
14 A Hebb szabály IV. Felhasználhajuk az időzíesége is, vagyis az, hogy a ké sejnek szimulán kell üzelni. Ez egyfaja ÉS kapcsola a sejek közö. Ha F ( ) egy jól viselkedő függvény, akkor Taylor sorba fejheő a v i = v j = 0 érékek körül. Ekkor a korbbi képle: dw ij = c 0 (w ij ) + c pos 1 (w ij )v i + c pre 1 d (w ij)v j + +c pos 2 (w ij )vi 2 + c pre 2 (w ij)vj 2 + c corr 2 (w ij )v i v j + O(v 3 ) A ké sej akiviásának kapcsolaá a c corr 2 (w ij )- aralmazó ag írja le. Ha ez az együhaó poziív konsansnak válaszjuk, a Hebb szabály kapjuk: dw ij () d = Cv i ()v j (), C > 0 Ani-Hebb ípusúnak nevezzük azoka a szabályoka, ahol C < 0.
15 A Hebb szabály V. Variációk a Hebb szabályra Az eredei Hebb szabály szerin a szinapszisok erősödhenek a végelenségig. Ez kiküszöbölendő válaszhaó: c corr 2 (w ij ) = γ 2 (1 w ij ). A szinapszisok gyengülésé (felejés?) előálĺıhajuk, ha c 0 (w ij ) = γ 0 w ij. Ezzel a kövekező szabály kaphajuk: dw ij d = γ 2 (1 w ij )v i v j γ 0 w ij Az olyan szabályoka, melyek nem esznek elege valamely hebbi feléelnek (pl. a feni) nem- Hebb ípusú szabálynak nevezzük. Egyes szinapikus súlyok csökkenheőek úgy is, ha versengés vezeünk be az egyes szinapszisok közö, pl. a szinapszisok összegének normálásával. Egy ilyen szabály a lokaliás séri.
16 A Hebb szabály VI. Újabb variációk a Hebb szabályra Posz-szinapikus gaing: dw ij d = γv i (v j v Θ (w ij )) A posz-szinapikus neuron üzelése: homoszinapikus LTP-hez, azaz az akív pályák erősödéséhez és ugyanekkor heeroszinapikus LTD-hez, azaz az inakív szinapszisok gyengüléséhez veze. Spec. ese: dw ij d = v i (v j w ij ). Ilyenkor a pre-szinapikus üzelésmináza a szinapikus súlyokban árolódik. (Sac. eseben dw ij d = 0) Pre-szinapikus gaing: dw ij d = γ(v i v Θ (w ij ))v j Ha γ < 0 és v j -k konsansok a v i posz-szinapikus üzelési ráa sacionárius eseben a v Θ referencia érékhez konvergál.
17 A Hebb szabály VII. Még újabb variációk a Hebb szabályra Oja szabály: dw ij d = γ(v i v j w ij v 2 i ) A szinapikus súlyok aszimpoikusan konvergálnak a j w ij = 1 normálási feléelhez. Ez versengés jelen az ado posz-szinapikus sejekre érkező szinapszisok közö anélkül, hogy ez explicien benne lenne a szabályban. Kovariancia szabály: dw ij d = γ(v i v i )(v j v j ) Bienensock-Cooper-Munroe (BCM) szabály: dw ij d Φ 0 v 0 LTD v θ LTP v i = ηφ(v i v i )v j γw ij Ez a szabály egy fajája a pre-szinapikus gaingnek. LTP- és LTD- (Long Term Depression = a szinapszisok hosszú ávú gyengülése) is ud. (Ha v i helye v Θ van, az insabil fixpon.)
18 Modellek az idegrendszer-kuaásban - ELTE TTK, 2003 avaszi félév hp:// Lengyel Máé: Szinapszis-Plasziciás / 9
19 Modellek az idegrendszer-kuaásban - ELTE TTK, 2003 avaszi félév hp:// Lengyel Máé: Szinapszis-Plasziciás / 10
5. Differenciálegyenlet rendszerek
 5 Differenciálegyenle rendszerek Elsőrendű explici differenciálegyenle rendszer álalános alakja: d = f (, x, x,, x n ) d = f (, x, x,, x n ) (5) n d = f n (, x, x,, x n ) ömörebben: d = f(, x) Definíció:
5 Differenciálegyenle rendszerek Elsőrendű explici differenciálegyenle rendszer álalános alakja: d = f (, x, x,, x n ) d = f (, x, x,, x n ) (5) n d = f n (, x, x,, x n ) ömörebben: d = f(, x) Definíció:
Tanulás az idegrendszerben. Structure Dynamics Implementation Algorithm Computation - Function
 Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2010/2011 1/363
 1/363 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2010/2011 Az Előadások Témái -hálók 306/363 Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák
1/363 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2010/2011 Az Előadások Témái -hálók 306/363 Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák
Tanulás az idegrendszerben. Structure Dynamics Implementation Algorithm Computation - Function
 Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
Tanulás az idegrendszerben. Structure Dynamics Implementation Algorithm Computation - Function
 Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin 3 ÉETTSÉG VZSG 04. május 0. EEKTONK PSMEETEK KÖZÉPSZNTŰ ÍÁSBE ÉETTSÉG VZSG JVÍTÁS-ÉTÉKEÉS ÚTMTTÓ EMBE EŐFOÁSOK MNSZTÉM Egyszerű, rövid feladaok Maximális ponszám: 40.)
Elekronikai alapismereek középszin 3 ÉETTSÉG VZSG 04. május 0. EEKTONK PSMEETEK KÖZÉPSZNTŰ ÍÁSBE ÉETTSÉG VZSG JVÍTÁS-ÉTÉKEÉS ÚTMTTÓ EMBE EŐFOÁSOK MNSZTÉM Egyszerű, rövid feladaok Maximális ponszám: 40.)
GAZDASÁGI ÉS ÜZLETI STATISZTIKA jegyzet ÜZLETI ELŐREJELZÉSI MÓDSZEREK
 BG PzK Módszerani Inézei Tanszéki Oszály GAZDAÁGI É ÜZLETI TATIZTIKA jegyze ÜZLETI ELŐREJELZÉI MÓDZEREK A jegyzee a BG Módszerani Inézei Tanszékének okaói készíeék 00-ben. Az idősoros vizsgálaok legfonosabb
BG PzK Módszerani Inézei Tanszéki Oszály GAZDAÁGI É ÜZLETI TATIZTIKA jegyze ÜZLETI ELŐREJELZÉI MÓDZEREK A jegyzee a BG Módszerani Inézei Tanszékének okaói készíeék 00-ben. Az idősoros vizsgálaok legfonosabb
3. Mekkora feszültségre kell feltölteni egy defibrillátor 20 μf kapacitású kondenzátorát, hogy a defibrilláló impulzus energiája 160 J legyen?
 Impulzusgeneráorok. a) Mekkora kapaciású kondenzáor alko egy 0 MΩ- os ellenállással s- os időállandójú RC- kör? b) Ezen RC- kör kisüésekor az eredei feszülségnek hány %- a van még meg s múlva?. Egy RC-
Impulzusgeneráorok. a) Mekkora kapaciású kondenzáor alko egy 0 MΩ- os ellenállással s- os időállandójú RC- kör? b) Ezen RC- kör kisüésekor az eredei feszülségnek hány %- a van még meg s múlva?. Egy RC-
Túlgerjesztés elleni védelmi funkció
 Túlgerjeszés elleni védelmi unkció Budapes, 2011. auguszus Túlgerjeszés elleni védelmi unkció Bevezeés A úlgerjeszés elleni védelmi unkció generáorok és egységkapcsolású ranszormáorok vasmagjainak úlzoan
Túlgerjeszés elleni védelmi unkció Budapes, 2011. auguszus Túlgerjeszés elleni védelmi unkció Bevezeés A úlgerjeszés elleni védelmi unkció generáorok és egységkapcsolású ranszormáorok vasmagjainak úlzoan
Dinamikus optimalizálás és a Leontief-modell
 MÛHELY Közgazdasági Szemle, LVI. évf., 29. január (84 92. o.) DOBOS IMRE Dinamikus opimalizálás és a Leonief-modell A anulmány a variációszámíás gazdasági alkalmazásaiból ismere hárma. Mind három alkalmazás
MÛHELY Közgazdasági Szemle, LVI. évf., 29. január (84 92. o.) DOBOS IMRE Dinamikus opimalizálás és a Leonief-modell A anulmány a variációszámíás gazdasági alkalmazásaiból ismere hárma. Mind három alkalmazás
HF1. Határozza meg az f t 5 2 ugyanabban a koordinátarendszerben. Mi a lehetséges legbővebb értelmezési tartománya és
 Házi feladaok megoldása 0. nov. 6. HF. Haározza meg az f 5 ugyanabban a koordináarendszerben. Mi a leheséges legbővebb érelmezési arománya és érékkészlee az f és az f függvényeknek? ( ) = függvény inverzé.
Házi feladaok megoldása 0. nov. 6. HF. Haározza meg az f 5 ugyanabban a koordináarendszerben. Mi a leheséges legbővebb érelmezési arománya és érékkészlee az f és az f függvényeknek? ( ) = függvény inverzé.
Intraspecifikus verseny
 Inraspecifikus verseny Források limiálsága evolúciós (finesz) kövekezmény aszimmeria Denziás-függés Park és msai (930-as évek, Chicago) - Tribolium casaneum = denziás-függelen (D-ID) 2 = alulkompenzál
Inraspecifikus verseny Források limiálsága evolúciós (finesz) kövekezmény aszimmeria Denziás-függés Park és msai (930-as évek, Chicago) - Tribolium casaneum = denziás-függelen (D-ID) 2 = alulkompenzál
Mikroelektródás képalkotó eljárások Somogyvári Zoltán
 Somogyvári Zoltán Magyar Tudományos Akadémia Wigner Fizikai Kutatóközpont Részecske és Magfizikai Intézet Elméleti Osztály Elméleti Idegtudomány és Komplex Rendszerek Kutatócsoport Az agy szürkeállománya
Somogyvári Zoltán Magyar Tudományos Akadémia Wigner Fizikai Kutatóközpont Részecske és Magfizikai Intézet Elméleti Osztály Elméleti Idegtudomány és Komplex Rendszerek Kutatócsoport Az agy szürkeállománya
ELTE TáTK Közgazdaságtudományi Tanszék GAZDASÁGSTATISZTIKA. Készítette: Bíró Anikó. Szakmai felelős: Bíró Anikó június
 GAZDASÁGSTATISZTIKA GAZDASÁGSTATISZTIKA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004pályázai projek kereében Taralomfejleszés az ELTE TáK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék, az
GAZDASÁGSTATISZTIKA GAZDASÁGSTATISZTIKA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004pályázai projek kereében Taralomfejleszés az ELTE TáK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék, az
Jegyzőkönyv. fajhő méréséről 5
 egyzőkönyv a fajhő méréséről 5 Készíee: Tüzes Dániel Mérés ideje: szerda 14 18 óra egyzőkönyv elkészüle: 8 9 4 A mérés célja A felada egy szilárd anyag fém fajhőjének közelíő meghaározása. Ugyan ma már
egyzőkönyv a fajhő méréséről 5 Készíee: Tüzes Dániel Mérés ideje: szerda 14 18 óra egyzőkönyv elkészüle: 8 9 4 A mérés célja A felada egy szilárd anyag fém fajhőjének közelíő meghaározása. Ugyan ma már
13 Wiener folyamat és az Itô lemma. Options, Futures, and Other Derivatives, 8th Edition, Copyright John C. Hull
 13 Wiener folyama és az Iô lemma Opions, Fuures, and Oher Derivaives, 8h Ediion, Copyrigh John C. Hull 01 1 Markov folyamaok Memória nélküli szochaszikus folyamaok, a kövekező lépés csak a pillananyi helyzeől
13 Wiener folyama és az Iô lemma Opions, Fuures, and Oher Derivaives, 8h Ediion, Copyrigh John C. Hull 01 1 Markov folyamaok Memória nélküli szochaszikus folyamaok, a kövekező lépés csak a pillananyi helyzeől
Transzportfolyamatok a biológiai rendszerekben
 A nyugalmi potenciál jelentősége Transzportfolyamatok a biológiai rendszerekben Transzportfolyamatok a sejt nyugalmi állapotában a sejt homeosztázisának (sejttérfogat, ph) fenntartása ingerlékenység érzékelés
A nyugalmi potenciál jelentősége Transzportfolyamatok a biológiai rendszerekben Transzportfolyamatok a sejt nyugalmi állapotában a sejt homeosztázisának (sejttérfogat, ph) fenntartása ingerlékenység érzékelés
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin Javíási-érékelési úmuaó 063 ÉETTSÉG VZSG 006. okóber 4. EEKTONK PSMEETEK KÖZÉPSZNTŰ ÍÁSE ÉETTSÉG VZSG JVÍTÁS-ÉTÉKEÉS ÚTMTTÓ OKTTÁS ÉS KTÁS MNSZTÉM Elekronikai alapismereek
Elekronikai alapismereek középszin Javíási-érékelési úmuaó 063 ÉETTSÉG VZSG 006. okóber 4. EEKTONK PSMEETEK KÖZÉPSZNTŰ ÍÁSE ÉETTSÉG VZSG JVÍTÁS-ÉTÉKEÉS ÚTMTTÓ OKTTÁS ÉS KTÁS MNSZTÉM Elekronikai alapismereek
6. szemináriumi. Gyakorló feladatok. Tőkekínálat. Tőkekereslet. Várható vs váratlan esemény tőkepiaci hatása. feladatok
 6. szemináriumi Gyakorló feladaok. Tőkekínála. Tőkekeresle. Várhaó vs váralan esemény őkepiaci haása. feladaok A feladaok megoldása során ahol lehe, írjon MATLAB scripe!!! Figyelem, a MATLAB a gondolkodás
6. szemináriumi Gyakorló feladaok. Tőkekínála. Tőkekeresle. Várhaó vs váralan esemény őkepiaci haása. feladaok A feladaok megoldása során ahol lehe, írjon MATLAB scripe!!! Figyelem, a MATLAB a gondolkodás
Opkut 2. zh tematika
 Opku. zh emaika. Maximáli folyam felada do egy irányío gráf, az éleken aló é felő korláok, kereünk maximáli folyamo! Ha neked kell kezdő megengede folyamo alálni, akkor 0 aló korláokra lehe zámíani. Ha
Opku. zh emaika. Maximáli folyam felada do egy irányío gráf, az éleken aló é felő korláok, kereünk maximáli folyamo! Ha neked kell kezdő megengede folyamo alálni, akkor 0 aló korláokra lehe zámíani. Ha
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin Javíási-érékelési úmaó 09 ÉETTSÉGI VIZSG 00. májs 4. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ OKTTÁSI ÉS KULTUÁLIS MINISZTÉIUM
Elekronikai alapismereek középszin Javíási-érékelési úmaó 09 ÉETTSÉGI VIZSG 00. májs 4. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ OKTTÁSI ÉS KULTUÁLIS MINISZTÉIUM
Aggregált termeléstervezés
 Aggregál ermeléservezés Az aggregál ermeléservezés feladaa az opimális ermékszerkeze valamin a gyáráshoz felhasználhaó erőforrások opimális szinjének meghaározása. Termékek aggregálása. Erőforrások aggregálása.
Aggregál ermeléservezés Az aggregál ermeléservezés feladaa az opimális ermékszerkeze valamin a gyáráshoz felhasználhaó erőforrások opimális szinjének meghaározása. Termékek aggregálása. Erőforrások aggregálása.
1. Feladatkör: nemzeti számvitel. Mikro- és makroökonómia
 Mikro- és makroökonómia Felada: hielpénzrendszer működése (egyszerűsíe Rosier-modell) Tekinsünk egy zár isza hielpénz-gazdaságo, ahol minden arozás a kövekező időszakban kell visszaadni és a bank egyálalán
Mikro- és makroökonómia Felada: hielpénzrendszer működése (egyszerűsíe Rosier-modell) Tekinsünk egy zár isza hielpénz-gazdaságo, ahol minden arozás a kövekező időszakban kell visszaadni és a bank egyálalán
Fourier-sorok konvergenciájáról
 Fourier-sorok konvergenciájáról A szereplő függvényekről mindenü felesszük, hogy szerin periodikusak. Az ilyen függvények megközelíésére (nem a polinomok, hanem) a rigonomerikus polinomok űnnek ermészees
Fourier-sorok konvergenciájáról A szereplő függvényekről mindenü felesszük, hogy szerin periodikusak. Az ilyen függvények megközelíésére (nem a polinomok, hanem) a rigonomerikus polinomok űnnek ermészees
Instrumentális változók módszerének alkalmazásai Mikroökonometria, 3. hét Bíró Anikó Kereslet becslése: folytonos választás modell
 Insrumenális válozók módszerének alkalmazásai Mikroökonomeria, 3. hé Bíró Anikó Keresle becslése: folyonos válaszás modell Folyonos vs. diszkré válaszás: elérő modellek Felevés: homogén jószág Közelíés:
Insrumenális válozók módszerének alkalmazásai Mikroökonomeria, 3. hé Bíró Anikó Keresle becslése: folyonos válaszás modell Folyonos vs. diszkré válaszás: elérő modellek Felevés: homogén jószág Közelíés:
Vezetéki termikus védelmi funkció
 Budapes, 016. auguszus Bevezeés A vezeéki ermikus védelmi fukció alapveőe a három miavéeleze fázisáramo méri. Kiszámolja az effekív érékeke, és a hőmérsékle számíásá a fázisáramok effekív érékére alapozza.
Budapes, 016. auguszus Bevezeés A vezeéki ermikus védelmi fukció alapveőe a három miavéeleze fázisáramo méri. Kiszámolja az effekív érékeke, és a hőmérsékle számíásá a fázisáramok effekív érékére alapozza.
Statisztika II. előadás és gyakorlat 1. rész
 Saiszika II. Saiszika II. előadás és gyakorla 1. rész T.Nagy Judi Ajánlo irodalom: Ilyésné Molnár Emese Lovasné Avaó Judi: Saiszika II. Feladagyűjemény, Perfek, 2006. Korpás Ailáné (szerk.): Álalános Saiszika
Saiszika II. Saiszika II. előadás és gyakorla 1. rész T.Nagy Judi Ajánlo irodalom: Ilyésné Molnár Emese Lovasné Avaó Judi: Saiszika II. Feladagyűjemény, Perfek, 2006. Korpás Ailáné (szerk.): Álalános Saiszika
Egy idegsejt működése. a. Nyugalmi potenciál b. Transzport proteinek c. Akciós potenciál
 Egy idegsejt működése a. Nyugalmi potenciál b. Transzport proteinek c. Akciós potenciál Nyugalmi potenciál Az ionok vándorlása 5. Alacsonyabb koncentráció ioncsatorna membrán Passzív Aktív 3 tényező határozza
Egy idegsejt működése a. Nyugalmi potenciál b. Transzport proteinek c. Akciós potenciál Nyugalmi potenciál Az ionok vándorlása 5. Alacsonyabb koncentráció ioncsatorna membrán Passzív Aktív 3 tényező határozza
Előszó. 1. Rendszertechnikai alapfogalmak.
 Plel Álalános áekinés, jel és rendszerechnikai alapfogalmak. Jelek feloszása (folyonos idejű, diszkré idejű és folyonos érékű, diszkré érékű, deerminiszikus és szochaszikus. Előszó Anyagi világunkban,
Plel Álalános áekinés, jel és rendszerechnikai alapfogalmak. Jelek feloszása (folyonos idejű, diszkré idejű és folyonos érékű, diszkré érékű, deerminiszikus és szochaszikus. Előszó Anyagi világunkban,
Synchronization of cluster-firing cells in the medial septum
 Synchronization of cluster-firing cells in the medial septum Balázs Ujfalussy and Tamás Kiss 25. december 9. Tartalom Miért burstöl a Wang-féle sejt? - bifurkációk Xpp-vel. Az ANDREW-project második félideje
Synchronization of cluster-firing cells in the medial septum Balázs Ujfalussy and Tamás Kiss 25. december 9. Tartalom Miért burstöl a Wang-féle sejt? - bifurkációk Xpp-vel. Az ANDREW-project második félideje
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin ÉETTSÉG VZSGA 0. május. ELEKTONKA ALAPSMEETEK KÖZÉPSZNTŰ ÍÁSBEL ÉETTSÉG VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ EMBE EŐFOÁSOK MNSZTÉMA Egyszerű, rövid feladaok Maximális ponszám:
Elekronikai alapismereek középszin ÉETTSÉG VZSGA 0. május. ELEKTONKA ALAPSMEETEK KÖZÉPSZNTŰ ÍÁSBEL ÉETTSÉG VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ EMBE EŐFOÁSOK MNSZTÉMA Egyszerű, rövid feladaok Maximális ponszám:
3. feladatsor: Görbe ívhossza, görbementi integrál (megoldás)
 Maemaika A3 gyakorla Energeika és Mecharonika BSc szakok, 6/7 avasz 3. feladasor: Görbe ívhossza, görbemeni inegrál megoldás. Mi az r 3 3 i + 6 5 5 j + 9 k görbe ívhossza a [, ] inervallumon? A megado
Maemaika A3 gyakorla Energeika és Mecharonika BSc szakok, 6/7 avasz 3. feladasor: Görbe ívhossza, görbemeni inegrál megoldás. Mi az r 3 3 i + 6 5 5 j + 9 k görbe ívhossza a [, ] inervallumon? A megado
a. Nyugalmi potenciál b. Transzport proteinek c. Akciós potenciál. Nyugalmi potenciál. 3 tényező határozza meg:
 Egy idegsejt működése a. Nyugalmi potenciál b. Transzport proteinek c. Nyugalmi potenciál Az ionok vándorlása 5. Alacsonyabb koncentráció ioncsatorna membrán Passzív Aktív 3 tényező határozza meg: 1. Koncentráció
Egy idegsejt működése a. Nyugalmi potenciál b. Transzport proteinek c. Nyugalmi potenciál Az ionok vándorlása 5. Alacsonyabb koncentráció ioncsatorna membrán Passzív Aktív 3 tényező határozza meg: 1. Koncentráció
) (11.17) 11.2 Rácsos tartók párhuzamos övekkel
 Rácsos arók párhuzamos övekkel Azér, hog a sabiliási eléelek haásá megvizsgáljuk, eg egszerű síkbeli, saikailag haározo, K- rácsozású aró vizsgálunk párhuzamos övekkel és hézagos csomóponokkal A rúdelemek
Rácsos arók párhuzamos övekkel Azér, hog a sabiliási eléelek haásá megvizsgáljuk, eg egszerű síkbeli, saikailag haározo, K- rácsozású aró vizsgálunk párhuzamos övekkel és hézagos csomóponokkal A rúdelemek
3. Gyakorlat. A soros RLC áramkör tanulmányozása
 3. Gyakorla A soros áramkör anlmányozása. A gyakorla célkiőzései Válakozó áramú áramkörökben a ekercsek és kondenzáorok frekvenciafüggı reakív ellenállással ún. reakanciával rendelkeznek. Sajáságos lajdonságaik
3. Gyakorla A soros áramkör anlmányozása. A gyakorla célkiőzései Válakozó áramú áramkörökben a ekercsek és kondenzáorok frekvenciafüggı reakív ellenállással ún. reakanciával rendelkeznek. Sajáságos lajdonságaik
Elektronika 2. TFBE1302
 Elekronika. TFE30 Analóg elekronika áramköri elemei TFE30 Elekronika. Analóg elekronika Elekronika árom fő ága: Analóg elekronika A jelordozó mennyiség érékkészlee az érelmezési arományon belül folyonos.
Elekronika. TFE30 Analóg elekronika áramköri elemei TFE30 Elekronika. Analóg elekronika Elekronika árom fő ága: Analóg elekronika A jelordozó mennyiség érékkészlee az érelmezési arományon belül folyonos.
GAZDASÁGSTATISZTIKA. Készítette: Bíró Anikó. Szakmai felelős: Bíró Anikó. 2010. június
 GAZDASÁGSTATISZTIKA Készül a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázai projek kereében Taralomfejleszés az ELTE TáTK Közgazdaságudományi Tanszékén, az ELTE Közgazdaságudományi Tanszék, az MTA Közgazdaságudományi
GAZDASÁGSTATISZTIKA Készül a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázai projek kereében Taralomfejleszés az ELTE TáTK Közgazdaságudományi Tanszékén, az ELTE Közgazdaságudományi Tanszék, az MTA Közgazdaságudományi
.1. A sinx és cosx racionális függvényeinek integrálásáa. = R sinx,cosx dx. x x 2. 1 dt
 . Trigonomeriai fügvények inegrálása Egy J függvény ípusáól függ. R x inegrál kiszámíása az R x racionális.. A sinx és cosx racionális függvényeinek inegrálásáa negrál J R sinxcosx Helyeesíés () R A és
. Trigonomeriai fügvények inegrálása Egy J függvény ípusáól függ. R x inegrál kiszámíása az R x racionális.. A sinx és cosx racionális függvényeinek inegrálásáa negrál J R sinxcosx Helyeesíés () R A és
A kémiai szinapszis (alapok)
 A preszinapszis A kémiai szinapszis (alapok) preszinaptikus neuron 1 akciós potenciál 2 Ca 2+ axon végbunkó (preszinapszis) Ca 2+ szinaptikus vezikula feszültség-függő Ca 2+ csatorna citoplazma szinaptikus
A preszinapszis A kémiai szinapszis (alapok) preszinaptikus neuron 1 akciós potenciál 2 Ca 2+ axon végbunkó (preszinapszis) Ca 2+ szinaptikus vezikula feszültség-függő Ca 2+ csatorna citoplazma szinaptikus
ELTE TáTK Közgazdaságtudományi Tanszék ÖKONOMETRIA. Készítette: Elek Péter, Bíró Anikó. Szakmai felelős: Elek Péter június
 ÖKONOMETRIA ÖKONOMETRIA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004pályázai projek kereében Taralomfejleszés az ELTE TáK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék, az MTA Közgazdaságudományi
ÖKONOMETRIA ÖKONOMETRIA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004pályázai projek kereében Taralomfejleszés az ELTE TáK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék, az MTA Közgazdaságudományi
ELTE TáTK Közgazdaságtudományi Tanszék GAZDASÁGSTATISZTIKA. Készítette: Bíró Anikó. Szakmai felelős: Bíró Anikó. 2010. június
 GAZDASÁGSTATISZTIKA GAZDASÁGSTATISZTIKA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004pályázai projek kereében Taralomfejleszés az ELTE TáK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék, az
GAZDASÁGSTATISZTIKA GAZDASÁGSTATISZTIKA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004pályázai projek kereében Taralomfejleszés az ELTE TáK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék, az
Szinkron sorrendi hálózatok tervezése
 Szinkron sorrendi hálózaok ervezése Benesóczky Zolán 24 A jegyzee a szerzői jog védi. Az a BME hallgaói használhaják, nyomahaják anulás céljából. Minden egyéb felhasználáshoz a szerző belegyezése szükséges.
Szinkron sorrendi hálózaok ervezése Benesóczky Zolán 24 A jegyzee a szerzői jog védi. Az a BME hallgaói használhaják, nyomahaják anulás céljából. Minden egyéb felhasználáshoz a szerző belegyezése szükséges.
5. HŐMÉRSÉKLETMÉRÉS 1. Hőmérséklet, hőmérők Termoelemek
 5. HŐMÉRSÉKLETMÉRÉS 1. Hőmérsékle, hőmérők A hőmérsékle a esek egyik állapohaározója. A hőmérsékle a es olyan sajáossága, ami meghaározza, hogy a es ermikus egyensúlyban van-e más esekkel. Ezen alapszik
5. HŐMÉRSÉKLETMÉRÉS 1. Hőmérsékle, hőmérők A hőmérsékle a esek egyik állapohaározója. A hőmérsékle a es olyan sajáossága, ami meghaározza, hogy a es ermikus egyensúlyban van-e más esekkel. Ezen alapszik
Gyors kinetikai módszerek
 Dr. Kengyel ndrás Enzim-szubszrá Gyors folyamaok Recepor-ligand Gyors kineikai módszerek Lizozim - poliszacharid hp://pixshark.com/enzyme-acive-sie.hm Fehérje-gyógyszer Inzulin - recepor hp://www.riniy.edu/lespey/biol3449/lecures/lec10/lec10.hm
Dr. Kengyel ndrás Enzim-szubszrá Gyors folyamaok Recepor-ligand Gyors kineikai módszerek Lizozim - poliszacharid hp://pixshark.com/enzyme-acive-sie.hm Fehérje-gyógyszer Inzulin - recepor hp://www.riniy.edu/lespey/biol3449/lecures/lec10/lec10.hm
Rövid távú elôrejelzésre használt makorökonometriai modell*
 Tanulmányok Rövid ávú elôrejelzésre használ makorökonomeriai modell* Balaoni András, a Századvég Gazdaságkuaó Zr. kuaási igazgaója E-mail: balaoni@szazadveg-eco.hu Mellár Tamás, az MTA dokora, a Pécsi
Tanulmányok Rövid ávú elôrejelzésre használ makorökonomeriai modell* Balaoni András, a Századvég Gazdaságkuaó Zr. kuaási igazgaója E-mail: balaoni@szazadveg-eco.hu Mellár Tamás, az MTA dokora, a Pécsi
II. Egyenáramú generátorokkal kapcsolatos egyéb tudnivalók:
 Bolizsár Zolán Aila Enika -. Eyenáramú eneráorok (NEM ÉGLEGES EZÓ, TT HÁNYOS, HBÁT TATALMAZHAT!!!). Eyenáramú eneráorokkal kapcsolaos eyé univalók: a. alós eneráorok: Természeesen ieális eneráorok nem
Bolizsár Zolán Aila Enika -. Eyenáramú eneráorok (NEM ÉGLEGES EZÓ, TT HÁNYOS, HBÁT TATALMAZHAT!!!). Eyenáramú eneráorokkal kapcsolaos eyé univalók: a. alós eneráorok: Természeesen ieális eneráorok nem
Komáromi András * Orova Lászlóné ** MATEMATIKAI MODELLEK AZ INNOVÁCIÓ TERJEDÉSÉBEN
 Koároi András * Orova Lászlóné ** MATEMATIKAI MODELLEK AZ INNOVÁCIÓ TERJEDÉSÉBEN BEVEZETÉS Az új erék, echnológia elerjedésének iseree nélkülözheelen a erel cégek száára, ezér külföldi és hazai kuaók ár
Koároi András * Orova Lászlóné ** MATEMATIKAI MODELLEK AZ INNOVÁCIÓ TERJEDÉSÉBEN BEVEZETÉS Az új erék, echnológia elerjedésének iseree nélkülözheelen a erel cégek száára, ezér külföldi és hazai kuaók ár
Zsembery Levente VOLATILITÁS KOCKÁZAT ÉS VOLATILITÁS KERESKEDÉS
 Zsembery Levene VOLATILITÁS KOCKÁZAT ÉS VOLATILITÁS KERESKEDÉS PÉNZÜGYI INTÉZET BEFEKTETÉSEK TANSZÉK TÉMAVEZETŐ: DR. SZÁZ JÁNOS Zsembery Levene BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI ÉS ÁLLAMIGAZGATÁSI EGYETEM
Zsembery Levene VOLATILITÁS KOCKÁZAT ÉS VOLATILITÁS KERESKEDÉS PÉNZÜGYI INTÉZET BEFEKTETÉSEK TANSZÉK TÉMAVEZETŐ: DR. SZÁZ JÁNOS Zsembery Levene BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI ÉS ÁLLAMIGAZGATÁSI EGYETEM
DIPLOMADOLGOZAT Varga Zoltán 2012
 DIPLOMADOLGOZAT Varga Zolán 2012 Szen Isván Egyeem Gazdaság- és Társadalomudományi Kar Markeing Inéze Keresle-előrejelzés a vállalai logiszikában Belső konzulens neve, beoszása: Dr. Komáromi Nándor, egyeemi
DIPLOMADOLGOZAT Varga Zolán 2012 Szen Isván Egyeem Gazdaság- és Társadalomudományi Kar Markeing Inéze Keresle-előrejelzés a vállalai logiszikában Belső konzulens neve, beoszása: Dr. Komáromi Nándor, egyeemi
Csecsemő- és gyermeknevelőgondozó Csecsemő- és gyermeknevelőgondozó
 A 10/2007 (II. 27.) SzMM rendeleel módosío 1/2006 (II. 17.) OM rendele Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe örénő felvéel és örlés eljárási rendjéről alapján. Szakképesíés, szakképesíés-elágazás,
A 10/2007 (II. 27.) SzMM rendeleel módosío 1/2006 (II. 17.) OM rendele Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe örénő felvéel és örlés eljárási rendjéről alapján. Szakképesíés, szakképesíés-elágazás,
2.2.45. SZUPERKRITIKUS FLUID KROMATOGRÁFIA 2.2.46. KROMATOGRÁFIÁS ELVÁLASZTÁSI TECHNIKÁK
 2.2.45. Szuperkriikus fluid kromaográfia Ph. Hg. VIII. Ph. Eur. 4, 4.1 és 4.2 2.2.45. SZUPEKITIKUS FLUID KOATOGÁFIA A szuperkriikus fluid kromaográfia (SFC) olyan kromaográfiás elválaszási módszer, melyben
2.2.45. Szuperkriikus fluid kromaográfia Ph. Hg. VIII. Ph. Eur. 4, 4.1 és 4.2 2.2.45. SZUPEKITIKUS FLUID KOATOGÁFIA A szuperkriikus fluid kromaográfia (SFC) olyan kromaográfiás elválaszási módszer, melyben
8. előadás Ultrarövid impulzusok mérése - autokorreláció
 Ágazai Á felkészíés a hazai LI projekel összefüggő ő képzési é és KF feladaokra" " 8. előadás Ulrarövid impulzusok mérése - auokorreláció TÁMOP-4.1.1.C-1/1/KONV-1-5 projek 1 Bevezeés Jelen fejezeben áekinjük,
Ágazai Á felkészíés a hazai LI projekel összefüggő ő képzési é és KF feladaokra" " 8. előadás Ulrarövid impulzusok mérése - auokorreláció TÁMOP-4.1.1.C-1/1/KONV-1-5 projek 1 Bevezeés Jelen fejezeben áekinjük,
PÉNZÜGYMINISZTÉRIUM MUNKAANYAG A KÖLTSÉGVETÉSI RENDSZER MEGÚJÍTÁSÁNAK EGYES KÉRDÉSEIRŐL SZÓLÓ KONCEPCIÓ RÉSZLETES BEMUTATÁSA
 PÉNZÜGYMINISZTÉRIUM MUNKAANYAG A KÖLTSÉGVETÉSI RENDSZER MEGÚJÍTÁSÁNAK EGYES KÉRDÉSEIRŐL SZÓLÓ KONCEPCIÓ RÉSZLETES BEMUTATÁSA Függelék 2007. június Taralomjegyzék FÜGGELÉK. számú függelék: Az Országgyűlés
PÉNZÜGYMINISZTÉRIUM MUNKAANYAG A KÖLTSÉGVETÉSI RENDSZER MEGÚJÍTÁSÁNAK EGYES KÉRDÉSEIRŐL SZÓLÓ KONCEPCIÓ RÉSZLETES BEMUTATÁSA Függelék 2007. június Taralomjegyzék FÜGGELÉK. számú függelék: Az Országgyűlés
Módszertani megjegyzések a hitelintézetek összevont mérlegének alakulásáról szóló közleményhez
 Módszerani megjegyzések a hielinézeek összevon mérlegének alakulásáról szóló közleményhez 1. A forinosíás és az elszámolás kezelése a moneáris saiszikákban Az egyes fogyaszói kölcsönszerződések devizanemének
Módszerani megjegyzések a hielinézeek összevon mérlegének alakulásáról szóló közleményhez 1. A forinosíás és az elszámolás kezelése a moneáris saiszikákban Az egyes fogyaszói kölcsönszerződések devizanemének
Összegezés az ajánlatok elbírálásáról
 Összegezés az ajánlaok elbírálásáról 9. mellékle a 92/211. (XII. 3.) NFM rendelehez 1. Az ajánlakérő neve és címe: Budesi Távhőszolgálaó Zárkörűen Működő Részvényársaság (FŐTÁV Zr.) 1116 Budes Kaloaszeg
Összegezés az ajánlaok elbírálásáról 9. mellékle a 92/211. (XII. 3.) NFM rendelehez 1. Az ajánlakérő neve és címe: Budesi Távhőszolgálaó Zárkörűen Működő Részvényársaság (FŐTÁV Zr.) 1116 Budes Kaloaszeg
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017.
 Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Ahonnan letölthető az anyag (egy része):
 Ahonnan letölthető az anyag (egy része): www.rmki.kfki.hu/biofiz/cneuro/tutorials.html www.rmki.kfki.hu/ lmate/kurz/ A segédanyagokban az 1,3,4 előadások. itt található egy könyv, butler.cc.tut.fi/ malmivuo/bem/bembook/00/co.htm
Ahonnan letölthető az anyag (egy része): www.rmki.kfki.hu/biofiz/cneuro/tutorials.html www.rmki.kfki.hu/ lmate/kurz/ A segédanyagokban az 1,3,4 előadások. itt található egy könyv, butler.cc.tut.fi/ malmivuo/bem/bembook/00/co.htm
CELLULÁRIS SZÍV- ELEKTROFIZIOLÓGIAI MÉRÉSI TECHNIKÁK. Dr. Virág László
 CELLULÁRIS SZÍV- ELEKTROFIZIOLÓGIAI MÉRÉSI TECHNIKÁK Dr. Virág László Intracelluláris mikroelektród technika Voltage clamp technika Patch clamp technika Intracelluláris mikroelektród technika Ag/AgCl
CELLULÁRIS SZÍV- ELEKTROFIZIOLÓGIAI MÉRÉSI TECHNIKÁK Dr. Virág László Intracelluláris mikroelektród technika Voltage clamp technika Patch clamp technika Intracelluláris mikroelektród technika Ag/AgCl
Vezetéki termikus védelmi funkció
 Budaps, 011. április Bvzés A vzéki rmikus védlmi fukció alapvő a hárm miavélz fázisáram méri. Kiszámlja az ffkív érékk, és a hőmérsékl számíásá a fázisáramk ffkív érékér alapzza. A hőmérséklszámíás a rmikus
Budaps, 011. április Bvzés A vzéki rmikus védlmi fukció alapvő a hárm miavélz fázisáram méri. Kiszámlja az ffkív érékk, és a hőmérsékl számíásá a fázisáramk ffkív érékér alapzza. A hőmérséklszámíás a rmikus
DIFFÚZIÓ. BIOFIZIKA I Október 20. Bugyi Beáta
 BIOFIZIKA I 010. Okóber 0. Bugyi Beáa TRANSZPORTELENSÉGEK Transzpor folyama: egy fizikai mennyiség érbeli eloszlása megválozik Emlékezeő: ermodinamika 0. főéele az egyensúly álalános feléele TERMODINAMIKAI
BIOFIZIKA I 010. Okóber 0. Bugyi Beáa TRANSZPORTELENSÉGEK Transzpor folyama: egy fizikai mennyiség érbeli eloszlása megválozik Emlékezeő: ermodinamika 0. főéele az egyensúly álalános feléele TERMODINAMIKAI
Közgazdasági idősorok elemzése X-11/12 ARIMA eljárással
 Közgazdasági idősorok elemzése X-11/12 ARIMA eljárással 1. Az idősor-elemzés menee Az idősor-elemzés célja, hogy a közgazdasági aralmú idősor hosszú ávú és rövid ávú viselkedésé egyérelmű módon széválassza,
Közgazdasági idősorok elemzése X-11/12 ARIMA eljárással 1. Az idősor-elemzés menee Az idősor-elemzés célja, hogy a közgazdasági aralmú idősor hosszú ávú és rövid ávú viselkedésé egyérelmű módon széválassza,
Látás Nyelv - Emlékezet. ETE47A001/2016_17_1/
 Látás Nyelv - Emlékezet http://www.cogsci.bme.hu/~ktkuser/kurzusok/bm ETE47A001/2016_17_1/ A látás alapjai Általános elv AGY Külvilág TÁRGY Érzékszervek (periféria) Felszálló (afferens) pálya Kéregalatti
Látás Nyelv - Emlékezet http://www.cogsci.bme.hu/~ktkuser/kurzusok/bm ETE47A001/2016_17_1/ A látás alapjai Általános elv AGY Külvilág TÁRGY Érzékszervek (periféria) Felszálló (afferens) pálya Kéregalatti
A látás alapjai. Látás Nyelv Emlékezet. Általános elv. Neuron idegsejt Neuronális hálózatok. Cajal és Golgi 1906 Nobel Díj A neuron
 Látás Nyelv Emlékezet A látás alapjai Általános elv Külvilág TÁRGY Érzékszervek (periféria) Felszálló (afferens) pálya AGY Kéregalatti és kérgi területek Szenzoros, majd motoros és asszociációs területek
Látás Nyelv Emlékezet A látás alapjai Általános elv Külvilág TÁRGY Érzékszervek (periféria) Felszálló (afferens) pálya AGY Kéregalatti és kérgi területek Szenzoros, majd motoros és asszociációs területek
A membránpotenciál. A membránpotenciál mérése
 A membránpotenciál Elektromos potenciál különbség a membrán két oldala közt, E m Cink Galvani (1791) Réz ideg izom A membránpotenciál mérése Mérési elv: feszültségmérő áramkör Erősítő (feszültségmérő műszer)
A membránpotenciál Elektromos potenciál különbség a membrán két oldala közt, E m Cink Galvani (1791) Réz ideg izom A membránpotenciál mérése Mérési elv: feszültségmérő áramkör Erősítő (feszültségmérő műszer)
REAKCIÓKINETIKA ALAPFOGALMAK. Reakciókinetika célja
 REKCIÓKINETIK LPFOGLMK Reakiókineika élja. Reakiók idbeli lefuásának, idbeliségének vizsgálaa: miér gyors egy reakió, és miér lassú egy másik?. Hogyan függ a reakiók sebessége a hmérséklel? 3. Reakiók
REKCIÓKINETIK LPFOGLMK Reakiókineika élja. Reakiók idbeli lefuásának, idbeliségének vizsgálaa: miér gyors egy reakió, és miér lassú egy másik?. Hogyan függ a reakiók sebessége a hmérséklel? 3. Reakiók
Negyedik gyakorlat: Szöveges feladatok, Homogén fokszámú egyenletek Dierenciálegyenletek, Földtudomány és Környezettan BSc
 Negyedik gyakorla: Szöveges feladaok, Homogén fokszámú egyenleek Dierenciálegyenleek, Földudomány és Környezean BSc. Szöveges feladaok A zikában el forduló folyamaok nagy része széválaszhaó egyenleekkel
Negyedik gyakorla: Szöveges feladaok, Homogén fokszámú egyenleek Dierenciálegyenleek, Földudomány és Környezean BSc. Szöveges feladaok A zikában el forduló folyamaok nagy része széválaszhaó egyenleekkel
Képlékenyalakítás elméleti alapjai. Feszültségi állapot. Dr. Krállics György
 Képlékeyalakíás elmélei alapjai Feszülségi állapo Dr. Krállics György krallics@eik.bme.hu Az előadás sorá megismerjük: A érfogai és felülei erőke, a feszülség ezor. A feszülség ezor főérékei és főiráyai;
Képlékeyalakíás elmélei alapjai Feszülségi állapo Dr. Krállics György krallics@eik.bme.hu Az előadás sorá megismerjük: A érfogai és felülei erőke, a feszülség ezor. A feszülség ezor főérékei és főiráyai;
LIKVIDITÁS ÉS REÁLGAZDASÁG KAPCSOLATA Az Egyesült Államok példáján
 Szegedi Tudományegyeem Gazdaságudományi Kar Közgazdaságudományi Dokori Iskola Ács Aila LIKVIDITÁS ÉS REÁLGAZDASÁG KAPCSOLATA Az Egyesül Államok példáján Dokori érekezés ézisei Témavezeő: Dr. Boos Kaalin
Szegedi Tudományegyeem Gazdaságudományi Kar Közgazdaságudományi Dokori Iskola Ács Aila LIKVIDITÁS ÉS REÁLGAZDASÁG KAPCSOLATA Az Egyesül Államok példáján Dokori érekezés ézisei Témavezeő: Dr. Boos Kaalin
A somatomotoros rendszer
 A somatomotoros rendszer Motoneuron 1 Neuromuscularis junctio (NMJ) Vázizom A somatomotoros rendszer 1 Neurotranszmitter: Acetil-kolin Mire hat: Nikotinos kolinerg-receptor (nachr) Izom altípus A parasympathicus
A somatomotoros rendszer Motoneuron 1 Neuromuscularis junctio (NMJ) Vázizom A somatomotoros rendszer 1 Neurotranszmitter: Acetil-kolin Mire hat: Nikotinos kolinerg-receptor (nachr) Izom altípus A parasympathicus
A sejtek közöti kommunikáció formái. BsC II. Sejtélettani alapok Dr. Fodor János
 A sejtek közöti kommunikáció formái BsC II. Sejtélettani alapok Dr. Fodor János 2010. 03.19. I. Kommunikáció, avagy a sejtek informálják egymást Kémiai jelátvitel formái Az üzenetek kémiai úton történő
A sejtek közöti kommunikáció formái BsC II. Sejtélettani alapok Dr. Fodor János 2010. 03.19. I. Kommunikáció, avagy a sejtek informálják egymást Kémiai jelátvitel formái Az üzenetek kémiai úton történő
Tanulás és memória. A tanulás és a memória formái, agyi lokalizációjuk és celluláris mechanizmusok. Pszichofiziológia ea.
 Tanulás és memória A tanulás és a memória formái, agyi lokalizációjuk és celluláris mechanizmusok Pszichofiziológia ea., 2016, Bali Zsolt Mi a tanulás és a memória? A tanulás tartós belső reprezentációk
Tanulás és memória A tanulás és a memória formái, agyi lokalizációjuk és celluláris mechanizmusok Pszichofiziológia ea., 2016, Bali Zsolt Mi a tanulás és a memória? A tanulás tartós belső reprezentációk
Gépi tanulás a gyakorlatban. Lineáris regresszió
 Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek emel szin Javíási-érékelési úmuaó ÉETTSÉGI VIZSG 0. okóber. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ EMEI EŐFOÁSOK MINISZTÉIUM Elekronikai
Elekronikai alapismereek emel szin Javíási-érékelési úmuaó ÉETTSÉGI VIZSG 0. okóber. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ EMEI EŐFOÁSOK MINISZTÉIUM Elekronikai
GAZDASÁGSTATISZTIKA. Készítette: Bíró Anikó. Szakmai felelős: Bíró Anikó június
 GAZDASÁGSTATISZTIKA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004ályázai rojk krébn Taralomfjlszés az ELTE TáTK Közgazdaságudományi Tanszékén, az ELTE Közgazdaságudományi Tanszék, az MTA Közgazdaságudományi
GAZDASÁGSTATISZTIKA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004ályázai rojk krébn Taralomfjlszés az ELTE TáTK Közgazdaságudományi Tanszékén, az ELTE Közgazdaságudományi Tanszék, az MTA Közgazdaságudományi
Erőmű-beruházások értékelése a liberalizált piacon
 AZ ENERGIAGAZDÁLKODÁS ALAPJAI 1.3 2.5 Erőmű-beruházások érékelése a liberalizál piacon Tárgyszavak: erőmű-beruházás; piaci ár; kockáza; üzelőanyagár; belső kama. Az elmúl évek kaliforniai apaszalaai az
AZ ENERGIAGAZDÁLKODÁS ALAPJAI 1.3 2.5 Erőmű-beruházások érékelése a liberalizál piacon Tárgyszavak: erőmű-beruházás; piaci ár; kockáza; üzelőanyagár; belső kama. Az elmúl évek kaliforniai apaszalaai az
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek emel szin 05 ÉETTSÉGI VIZSGA 005. május 0. ELEKTONIKAI ALAPISMEETEK EMELT SZINTŰ ÉETTSÉGI VIZSGA Az írásbeli vizsga időarama: 0 perc JAVÍTÁSI-ÉTÉKELÉSI ÚTMTATÓ OKTATÁSI MINISZTÉIM
Elekronikai alapismereek emel szin 05 ÉETTSÉGI VIZSGA 005. május 0. ELEKTONIKAI ALAPISMEETEK EMELT SZINTŰ ÉETTSÉGI VIZSGA Az írásbeli vizsga időarama: 0 perc JAVÍTÁSI-ÉTÉKELÉSI ÚTMTATÓ OKTATÁSI MINISZTÉIM
Folyamatszemléleti lehetőségek az agro-ökoszisztémák modellezésében
 Folyamaszemlélei leheőségek az agro-ökosziszémák modellezésében Dokori (D) érekezés Ladányi Mára Témavezeő: Dr. Harnos Zsol, MHAS, egyeemi anár BCE, Kerészeudományi Kar, Maemaika és Informaika Tanszék
Folyamaszemlélei leheőségek az agro-ökosziszémák modellezésében Dokori (D) érekezés Ladányi Mára Témavezeő: Dr. Harnos Zsol, MHAS, egyeemi anár BCE, Kerészeudományi Kar, Maemaika és Informaika Tanszék
Demográfiai átmenet, gazdasági növekedés és a nyugdíjrendszer fenntarthatósága
 Közgazdasági Szemle LXI évf 204 november (279 38 o) Varga Gergely Demográfiai ámene gazdasági növekedés és a nyugdírendszer fennarhaósága Magyarországon a ársadalombizosíási nyugdírendszer finanszírozása
Közgazdasági Szemle LXI évf 204 november (279 38 o) Varga Gergely Demográfiai ámene gazdasági növekedés és a nyugdírendszer fennarhaósága Magyarországon a ársadalombizosíási nyugdírendszer finanszírozása
AUTOMATIKA. Dr. Tóth János
 UTOMTIK UTOMTIK Dr. Tóh János TERC Kf. udapes, 3 Dr. Tóh János, 3 3 Kézira lezárva:. november 9. ISN 978-963-9968-57-8 Kiadja a TERC Kereskedelmi és Szolgálaó Kf. Szakkönyvkiadó Üzleága, az 795-ben alapío
UTOMTIK UTOMTIK Dr. Tóh János TERC Kf. udapes, 3 Dr. Tóh János, 3 3 Kézira lezárva:. november 9. ISN 978-963-9968-57-8 Kiadja a TERC Kereskedelmi és Szolgálaó Kf. Szakkönyvkiadó Üzleága, az 795-ben alapío
A sztochasztikus idősorelemzés alapjai
 A szochaszikus idősorelemzés alapjai Ferenci Tamás BCE, Saiszika Tanszék amas.ferenci@medsa.hu 2011. december 19. Taralomjegyzék 1. Az idősorelemzés fogalma, megközelíései 2 1.1. Az idősor fogalma...................................
A szochaszikus idősorelemzés alapjai Ferenci Tamás BCE, Saiszika Tanszék amas.ferenci@medsa.hu 2011. december 19. Taralomjegyzék 1. Az idősorelemzés fogalma, megközelíései 2 1.1. Az idősor fogalma...................................
CELLULÁRIS SZÍV- ELEKTROFIZIOLÓGIAI MÉRÉSI TECHNIKÁK. Dr. Virág László
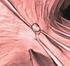 CELLULÁRIS SZÍV- ELEKTROFIZIOLÓGIAI MÉRÉSI TECHNIKÁK Dr. Virág László Intracelluláris mikroelektród technika Voltage clamp technika Patch clamp technika Membrane potentials and excitation of impaled single
CELLULÁRIS SZÍV- ELEKTROFIZIOLÓGIAI MÉRÉSI TECHNIKÁK Dr. Virág László Intracelluláris mikroelektród technika Voltage clamp technika Patch clamp technika Membrane potentials and excitation of impaled single
Elektronika 2. TFBE1302
 DE, Kísérlei Fizika Tanszék Elekronika 2. TFBE302 Jelparaméerek és üzemi paraméerek mérési módszerei TFBE302 Elekronika 2. DE, Kísérlei Fizika Tanszék Analóg elekronika, jelparaméerek Impulzus paraméerek
DE, Kísérlei Fizika Tanszék Elekronika 2. TFBE302 Jelparaméerek és üzemi paraméerek mérési módszerei TFBE302 Elekronika 2. DE, Kísérlei Fizika Tanszék Analóg elekronika, jelparaméerek Impulzus paraméerek
Tanulás az idegrendszerben
 Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Funkcióvezérelt modellezés Abból indulunk ki, hogy milyen feladatot valósít meg a rendszer Horace Barlow: "A
Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Funkcióvezérelt modellezés Abból indulunk ki, hogy milyen feladatot valósít meg a rendszer Horace Barlow: "A
GAZDASÁGPOLITIKA. Készítette: Pete Péter. Szakmai felelős: Pete Péter. 2011. június
 GAZDASÁGPOLITIKA Készül a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázai projek kereében Taralomfejleszés az ELTE TáTK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék az MTA Közgazdaságudományi
GAZDASÁGPOLITIKA Készül a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázai projek kereében Taralomfejleszés az ELTE TáTK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék az MTA Közgazdaságudományi
Az agykéreg és az agykérgi aktivitás mérése
 Az agykéreg és az agykérgi aktivitás mérése Intrakortikális hálózatok Elektromos aktiváció, sejtszintű integráció Intracelluláris sejtaktivitás mérés Sejten belüli elektromos integráció 70 mv mikroelektrod
Az agykéreg és az agykérgi aktivitás mérése Intrakortikális hálózatok Elektromos aktiváció, sejtszintű integráció Intracelluláris sejtaktivitás mérés Sejten belüli elektromos integráció 70 mv mikroelektrod
JELEK ALAPSÁVI LEÍRÁSA. MODULÁCIÓK. A CSATORNA LEÍRÁSA, TULAJDONSÁGAI.
 216. okóber 7., Budapes JELEK ALAPSÁVI LEÍRÁSA. MODULÁCIÓK. A CSATORNA LEÍRÁSA, TULAJDONSÁGAI. Alapfogalmak, fizikai réeg mindenki álal ismer fogalmak (hobbiból azér rákérdezheek vizsgán): jel, eljesímény,
216. okóber 7., Budapes JELEK ALAPSÁVI LEÍRÁSA. MODULÁCIÓK. A CSATORNA LEÍRÁSA, TULAJDONSÁGAI. Alapfogalmak, fizikai réeg mindenki álal ismer fogalmak (hobbiból azér rákérdezheek vizsgán): jel, eljesímény,
Numerikus matematika. Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, Lebegőpontos számok
 Numerikus matematika Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, 2007 Lebegőpontos számok Normák, kondíciószámok Lineáris egyenletrendszerek Legkisebb négyzetes
Numerikus matematika Irodalom: Stoyan Gisbert, Numerikus matematika mérnököknek és programozóknak, Typotex, 2007 Lebegőpontos számok Normák, kondíciószámok Lineáris egyenletrendszerek Legkisebb négyzetes
A nyugalmi potenciál megváltozása
 Akciós potenciál történelem A nyugalmi potenciál megváltozása 2. A membrán aktív elektromos tulajdonságai 1780: Luigi Galvani elektromos vezetés és izomösszehúzódás kapcsolata 1843: Emil Dubois-Reymond
Akciós potenciál történelem A nyugalmi potenciál megváltozása 2. A membrán aktív elektromos tulajdonságai 1780: Luigi Galvani elektromos vezetés és izomösszehúzódás kapcsolata 1843: Emil Dubois-Reymond
Numerikus módszerek 1.
 Numerikus módszerek 1. 11. előadás: A Newton-módszer és társai Lócsi Levente ELTE IK 2013. november 25. Tartalomjegyzék 1 A Newton-módszer és konvergenciatételei 2 Húrmódszer és szelőmódszer 3 Általánosítás
Numerikus módszerek 1. 11. előadás: A Newton-módszer és társai Lócsi Levente ELTE IK 2013. november 25. Tartalomjegyzék 1 A Newton-módszer és konvergenciatételei 2 Húrmódszer és szelőmódszer 3 Általánosítás
Tiszta és kevert stratégiák
 sza és kever sraégák sza sraéga: Az -edk áékos az sraégá és ez alkalmazza. S sraégahalmazból egyérelműen válasz k egy eknsük a kövekező áéko. Ké vállala I és II azonos erméke állí elő. Azon gondolkodnak,
sza és kever sraégák sza sraéga: Az -edk áékos az sraégá és ez alkalmazza. S sraégahalmazból egyérelműen válasz k egy eknsük a kövekező áéko. Ké vállala I és II azonos erméke állí elő. Azon gondolkodnak,
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Elektrotechnika 2. előadás
 Óudai Eyeem Bánki Doná Gépész és Bizonsáechnikai Kar Mecharonikai és Auechnikai néze Elekroechnika. előadás Összeállíoa: aner nrid adjunkus Szuperpozició-éel Generáorokól és lineáris impedanciákól álló
Óudai Eyeem Bánki Doná Gépész és Bizonsáechnikai Kar Mecharonikai és Auechnikai néze Elekroechnika. előadás Összeállíoa: aner nrid adjunkus Szuperpozició-éel Generáorokól és lineáris impedanciákól álló
Fizikai tulajdonságok mérések
 Épíőanyagok II - Laborgyakorla Fizikai ulajdonságok, érések A fizikai ulajdonságok csoporjai Töegeloszlással kapcsolaos ulajdonságok és vizsgálauk Fajlagos felüle egaározása Szecseére-eloszlás egaározása
Épíőanyagok II - Laborgyakorla Fizikai ulajdonságok, érések A fizikai ulajdonságok csoporjai Töegeloszlással kapcsolaos ulajdonságok és vizsgálauk Fajlagos felüle egaározása Szecseére-eloszlás egaározása
Prekoncepciók és téveszmék mint a fizikatanítás megnehezítői. Juhász András Ált isk. tanártovábbképzés 2014, okt. KPSZTI
 Prekoncepciók és téveszmék mint a fizikatanítás megnehezítői Juhász András Ált isk. tanártovábbképzés 2014, okt. KPSZTI Prof. Freund Tamás agykutató a tanulásról: (http://fiztan.phd.elte.hu/letolt/konfkotet2011.pdf
Prekoncepciók és téveszmék mint a fizikatanítás megnehezítői Juhász András Ált isk. tanártovábbképzés 2014, okt. KPSZTI Prof. Freund Tamás agykutató a tanulásról: (http://fiztan.phd.elte.hu/letolt/konfkotet2011.pdf
KELET-KÖZÉP EURÓPAI DEVIZAÁRFOLYAMOK ELİREJELZÉSE HATÁRIDİS ÁRFOLYAMOK SEGÍTSÉGÉVEL. Darvas Zsolt Schepp Zoltán
 Közgazdasági- és Regionális Tudományok Inézee Pécsi Tudományegyeem, Közgazdaságudományi Kar KELET-KÖZÉP EURÓPAI DEVIZAÁRFOLYAMOK ELİREJELZÉSE HATÁRIDİS ÁRFOLYAMOK SEGÍTSÉGÉVEL Darvas Zsol Schepp Zolán
Közgazdasági- és Regionális Tudományok Inézee Pécsi Tudományegyeem, Közgazdaságudományi Kar KELET-KÖZÉP EURÓPAI DEVIZAÁRFOLYAMOK ELİREJELZÉSE HATÁRIDİS ÁRFOLYAMOK SEGÍTSÉGÉVEL Darvas Zsol Schepp Zolán
Magasabb idegrendszeri folyamatok
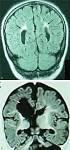 Magasabb idegrendszeri folyamatok Viselkedés A szenzoros bemenetekre adott (motoros) válasz. Az ember és állat viselkedését genetikusan kódolt, az egész szervezet szintjén érvényesülő idegi és kémiai faktorok
Magasabb idegrendszeri folyamatok Viselkedés A szenzoros bemenetekre adott (motoros) válasz. Az ember és állat viselkedését genetikusan kódolt, az egész szervezet szintjén érvényesülő idegi és kémiai faktorok
1. Előadás: Készletezési modellek, I-II.
 . Előadás: Készleezési modellek, I-II. Készleeke rendszerin azér arunk hogy, valamely szükséglee, igény kielégísünk. A szóban forgó anyag, cikk iráni igény, keresle a készle fogyásá idézi elő. Gondoskodnunk
. Előadás: Készleezési modellek, I-II. Készleeke rendszerin azér arunk hogy, valamely szükséglee, igény kielégísünk. A szóban forgó anyag, cikk iráni igény, keresle a készle fogyásá idézi elő. Gondoskodnunk
RÖVID TÁVÚ ELİREJELZİ MODELL MAGYARORSZÁGRA
 Közgazdasági és Regionális Tudományok Inézee Pécsi Tudományegyeem Közgazdaságudományi Kar MŐHELYTANULMÁNYOK RÖVID TÁVÚ ELİREJELZİ MODELL MAGYARORSZÁGRA Balaoni András - Mellár Tamás 2011/3 2011. szepember
Közgazdasági és Regionális Tudományok Inézee Pécsi Tudományegyeem Közgazdaságudományi Kar MŐHELYTANULMÁNYOK RÖVID TÁVÚ ELİREJELZİ MODELL MAGYARORSZÁGRA Balaoni András - Mellár Tamás 2011/3 2011. szepember
AZ IDEGSEJTEK KÖZTI SZINAPTIKUS KOMMUNIKÁCIÓ Hájos Norbert. Összefoglaló
 AZ IDEGSEJTEK KÖZTI SZINAPTIKUS KOMMUNIKÁCIÓ Hájos Norbert Összefoglaló Az idegsejtek közt az ingerületátvitel döntően kémiai természetű, míg az idegsejten belül az elektromos jelterjedés a jellemző. A
AZ IDEGSEJTEK KÖZTI SZINAPTIKUS KOMMUNIKÁCIÓ Hájos Norbert Összefoglaló Az idegsejtek közt az ingerületátvitel döntően kémiai természetű, míg az idegsejten belül az elektromos jelterjedés a jellemző. A
