SZOMSZÉDSÁGI SZEKVENCIÁK ÉS ALKALMAZÁSAIK A KÉPFELDOLGOZÁSBAN ÉS KÉPI ADATBÁZISOKBAN
|
|
|
- Amanda Szabóné
- 8 évvel ezelőtt
- Látták:
Átírás
1 SZOMSZÉDSÁGI SZEKVENCIÁK ÉS ALKALMAZÁSAIK A KÉPFELDOLGOZÁSBAN ÉS KÉPI ADATBÁZISOKBAN NEIGHBORHOOD SEQUENCES AND THEIR APPLICATIONS IN IMAGE PROCESSING AND IMAGE DATABASES András Hajdu, János Kormos, Tamás Tóth, Krisztián Veréb Debreceni Egyetem, Informatika Kar, Információ Technológia Tanszék 1. Bevezetés A különböz célú adatbázisokból való képek kinyerése napjainkban egy fontos alkalmazási és így egyúttal kutatási irány is. Ha egy adott képhez hasonlókat akarunk kinyerni az adatbázisból, akkor ezt több olyan tulajdonság vizsgálata alapján tehetjük meg, mint például a szín, a textúra (mintázat) vagy a képen lév objektumok alakja. Az általános eljárás, hogy ezekhez a tulajdonságokhoz tulajdonságvektorokat rendelünk, majd valamilyen távolságmér függvénnyel kiszámítjuk ezek normáját. Ez lesz a vizsgált kép és az adatbázisban lév képek közti távolság az adott tulajdonságra nézve. A különböz tulajdonságértékek kombinálásával pedig egy összevont távolságértéket definiálhatunk. Erre a célra az alkalmazások leggyakrabban a (súlyozott) euklideszi metrikát használják (lásd például Oracle 9i). Ebben a dolgozatban az összevont távolságmér függvények új megközelítését adjuk a szomszédsági szekvenciákon alapuló távolságmérés használatával. Megmutatjuk, hogy ez a megközelítés a klasszikus eljárásoknál rugalmasabb lekérések készítésére is alkalmas. A szomszédsági szekvenciák elméleténél maradva, a képi lekérdezések mellett bemutatunk néhány színeskép szegmentáló módszert is. A bemutatott módszerek klasszikus szegmentációs technikákra épülnek, azzal a különbséggel, hogy ismét a szomszédsági szekvenciák rugalmasabb távolságmérését használjuk az egyes színek hasonlóságának megállapításában. Mivel a színek koordinátái nemnegatív egészek (RGB), az ilyen távolságfogalmakra épül alkalmazások itt természetes módon használhatóak. A szomszédsági szekvenciák további érdekes tulajdonsága, hogy nem mindig generálnak metrikát, így lehet ség nyílik nem metrikus tulajdonságú távolságfüggvények alkalmazására is. A módszerünk az RGB modellen kívül kiterjeszthet más színreprezentációkra, illetve tetsz leges dimenzióra is. 2. Szomszédsági szekvenciák Ebben a fejezetben egy rövid összefoglalót közlünk a szomszédsági szekvenciákról. Az olvasó további elméleti és gyakorlati eredményeket találhat a [1,2,3,4,5,6,8,9,17,19] közleményekben. Legyen n egy tetsz leges pozitív egész. Legyen q és r két pont ZZ n -ben, Pr i (q) pedig jelölje a q pont i-edik koordinátáját. Legyen m egy egész, hogy 1 m n. A q és r pontok m-szomszédok, ha a következ két feltétel teljesül: Pri (q) Pr i (q) 1 (1 i n), n i= 1 Pr ( p) Pr ( q) m. i i
2 Az A=(A i ) i=1 sorozatot, ahol A i {1,, n} minden i IN, n-dimenziós szomszédsági szekvenciának nevezzük. Ha létezik valamilyen l IN, hogy A i+l = A i (i IN), akkor A periodikus szomszédsági szekvencia l periódushosszal. Ezt röviden az A = (A 1 A 2 A l ) formában írjuk. Például az A = {12} az {1,2,1,2,1,2, } szomszédsági szekvenciát jelenti. A q = q 0,q 1,,q m = r, pontsorozatot, ahol q i-1 és q i pontok A(i)-szomszédok ZZ n -ben (1 i m), q és r közti m-hosszú A-útnak nevezzük. A q és r közti A-utak közül a legrövidebb a két pont A-távolsága, melyet d(q,r;a)-val jelölünk. Ha egy szomszédsági szekvencia elejér l véges számú elemet eltávolítva periodikus szekvenciát kapunk, akkor ezt a sorozatot végén-periodikus szomszédsági szekvenciának nevezzük, és a következ jelölést használjuk: N = N 1 N 2 N k (N k+1 N k+2 N l ), vagyis az els k elem elvétele után l-k periódusú szomszédsági szekvenciát kapunk. A szomszédsági szekvenciák által generált távolságmér függvények nem mindig metrikák. Ez a tulajdonság egy egyszer feltétel segítségével könnyen ellen rizhet [12]. Az alkalmazásokban a nem metrikus távolságmér függvények is jó eredményt adhatnak, ezért nem indokolt a kizárásuk a további vizsgálatokból. 3. Szomszédsági szekvenciák képi adatbázisokhoz A szomszédsági szekvenciák adatbázis-lekérésekben való használhatóságának demonstrálásához három képi jellemz t rögzítünk: szín, textúra, alak. A három tulajdonságban való független hasonlóságok kvantitatív ismeretét feltételezve, egy összevont hasonlósági értéket készítünk a szomszédsági szekvenciák segítségével. Ehhez a háromdimenziós szekvenciák három két speciális családját és azok kombinációját tekintjük. Az els a klasszikus szomszédsági szekvenciák családja: B 1 = {(0, 0, ±1), (0, ±1, 0), (±1, 0, 0)} B 2 = B 1 {(0, ±1, ±1), (±1, 0, ±1), (±1, ±1, 0)} B 3 = B 2 {(±1, ±1, ±1)} A B 1, B 2 és B 3 szomszédságok a jól ismert 6-, 18- és 26-szomszédságnak felelnek meg. A fenti szomszédságok elméleti vizsgálatát lásd: [1,2,4,8]. Ezt a családot CNS 3 -nak nevezzük. A szomszédsági szekvenciák másik családjához tartoznak azok, amik explicit módon megadják, hogy két pont milyen koordináta-eltérés esetén szomszédja egymásnak. B x = {(±1, 0, 0)}, B y = {(0, ±1, 0)}, B z = {(0, 0, ±1)}, Bxy = {(±1, ±1, 0)}, B yz = {(0, ±1, ±1)}, B xz = {(±1, 0, ±1)}, B xyz = {(±1, ±1, ±1)} A megfelel szomszédságok 1, 2, illetve 3 dimenziós altereket feszítenek fel ZZ 3 -ban, ezért ezt a családot SNS 3 -nak nevezzük. SNS 3 szekvenciákkal megmondhatjuk, hogy egy lépés alatt melyik koordináták változhatnak, míg CNS 3 esetén azt, hogy hány koordináta változhat meg. Megjegyzend, hogy sem CNS 3 SNS 3 sem a fordított irány nem teljesül, továbbá, hogy B 3 = B xyz. A harmadik család a már bemutatott két család kombinációja, a használható szomszédságok: B 1, B 2, B 3, B x, B y, B z, B xy, B yz, B xz, B xyz. Ezt a családot MNS 3 -nak nevezzük. 4. Képadatbázis Oracle-ban
3 Hogy az elképzelésünket kipróbálhassuk a Hemera PhotoObjects képadatbázisból készítettünk egy több mint 1200 képet tartalmazó képadatbázist. Az Oracle segítségével generáltuk le a képek közti viszonyokat jellemz tulajdonságvektorokat (függetlenül a színre/textúrára/alakra vonatkozóan), és ezek segítségével valósítottuk meg a képkinyerést. Az Oracle-nak saját eszközrendszere van multimédiás anyagok tárolására és adatbázisból való elérésére. A képek színhisztogramját (c), textúrait (t), alakjait (s) és ezek elhelyezkedését (l) használja hasonlóságok leírására. Az elhelyezkedés (l) önmagában nem hordoz értékelhet információt, ezért ezt itt nem tekintjük érvényes keresési paraméterként. Egy adott lekérdezés esetén az Oracle kiszámolja a c, t, s hasonlósági értékeket az adatbázis minden képéhez, meghatározva így azokhoz (c, s, t) tulajdonságvektorokat, amelyek három, 0 és 100 közé es valós számból állnak. A független értékek összevont összehasonlíthatóságához 0 és 1 közé es súlyokat (W c, W s, W t ) rendelhetünk az egyes tulajdonságértékekhez. Ezzel megadhatjuk hogy az adott tulajdonság mennyire fontos a vizsgálat szempontjából: 0 jelzi, ha a tulajdonság elhanyagolható, 1, ha a legfontosabb. Az összevont távolságot az Oracle a következ módon számolja: c*w c + s*w s + t*w t. Hogy összehasonlíthassuk Oracle-t a saját technikánkkal, rendre hozzárendeltük az x, y és z koordinátákat a c szín, t textúra és s alak tulajdonságokhoz. A szomszédsági szekvenciák segítségével megválaszolható lekérdezésekre, illetve az Oracle esetén kapott válaszokkal való összehasonlításokra az Alkalmazás részben mutatunk példákat. 5. RGB távolságmérésen alapuló alkalmazások A színes képek szegmentálása els dlegesen a pixelek színének összehasonlításán alapul. Vizsgálatainkban a színek közti távolság mérésénél az RGB színkockát tekintjük, ami a fekete = (0, 0, 0) és a fehér = (255, 255, 255) szín közötti egész koordinátájú 3D-s tartományt jelenti. A színek közötti távolsáméréshez a szomszédsági szekvenciákat gondosan kell megválasztani, mivel a különböz szekvenciák alapvet en különböz eredményeket adhatnak [8]. Három szegmentációs módszert mutatunk be: els nek a fuzziness-t, (lásd Adobe Photoshop), majd a területnövelést, végül egy klaszterez módszert. Ismertetünk továbbá egy technikát, ami segítséget nyújthat a felhasználónak a megfelel távolságmér függvény kiválasztásában. Fuzziness. A módszer kiválogatja azokat a pixeleket, amelyeknek egy vagy több el re megadott színt l mért távolsága az adott távolságmér függvénnyel el re megadott korláton belül marad. A 1. ábra mutatja a módszer eredményének függését a távolságmér függvényt l. k = 50, {1} k = 50, {3} k = 50, {311111} 1. ábra Fuzziness, k = 50
4 Területnövelés. A fuzziness eredményeként több egymáshoz nem kapcsolódó tartományt kapunk. Hogy ezt kiküszöböljük, és csak egyetlen összefügg tartományt kapjunk, megadunk egy szomszédságot. A módszer ekkor azokat a pixeleket keresi, amelyeknek az el re kiválasztott pixel színét l az adott távolságmér függvénnyel mért távolsága az adott határon belül marad, és a pixelek egymásnak a megadott szomszédság szerint szomszédai, 2. ábra. Eredeti k = 70, {1} k = 100, {1} k = 40, {3} 2. ábra Területnövelés Szegmentálás. A módszerünk a klaszter-analízisre, mint statisztikai módszerre épít. Az RGB kocka elemeit vonjuk össze csoportokba. Két módszert használunk, a hierarchikus osztályozást és a k-közép módszert. Mindkét módszer esetében a színek közt szomszédsági szekvenciák által generált távolságmér függvényeket használunk, 3. ábra. Eredeti {1} {3} 3. ábra Szegmentálás Fuzziness hisztogram. Ez a fuzziness-hez közel álló módszer a fuzziness-hez és a területnöveléshez nyújthat segítséget. Egy hisztogramot készítünk, ahol az i-edik oszlop magassága arányos azoknak a pixeleknek a számával, amik az el re megadott színt l vagy színekt l a megadott távolságmér függvény szerint i lépés távolságra vannak. Természetesen a hisztogram alakja nagyban függ a kezd színekt l és a távolságmér függvényt l. Például egy gyorsabb függvény rövidebb hisztogramot eredményez, de fontos különbségek adódhatnak a hisztogram modalitására nézve is, 4. ábra. {1} {3} { } 4. ábra Fuzziness hisztogram 6. Alkalmazás Mivel az Oracle tulajdonságvektorai szín, alak és textúra alapján készülnek, képek kinyerésénél megmondhatjuk, hogy a fenti három tulajdonság közül melyik fontosabb a
5 többinél. Ha olyan képeket szeretnénk kapni, amik színben és textúrában hasonlítanak az eredeti képünkhöz, akkor ezeknek a tulajdonságokhoz nagyobb súlyt kell rendelnünk. Viszont ha a szomszédsági szekvenciákkal akarjuk a kérdést végrehajtani, meg kell adnunk, hogy melyik tulajdonság irányában hány lépést tehetünk meg, 5. ábra. Eredeti ábra {N xz 3 }{N y 40 } Megtehetjük, hogy id rendbe szedjük a tulajdonságokat, pl. ugyanannyi lépést tehetünk meg a szín irányában, mint textúra irányában, csak az egyik lekérdezésnél a szín irányába megyünk el bb, a másiknál a textúra irányába, és teljesen más eredményt kapunk, 6. ábra és 7. ábra. (Fels indexben jelezzük, hogy az adott szomszédság hányszor ismétl dik a szekvenciában) Eredeti ábra {N y 40 }{N x 4 }{N z 4 } Eredti ábra {N y 40 }{N z 4 }{N x 4 } Eredmények közlése nélkül bemutatunk egy példát. Szeretnénk karácsonyi képeket kiválogatni, vagyis azokat, amiken található egy karácsonyfa, vagy pedig sok rajtuk a zöld szín. Ha van egy zöld karácsonyfát tartalmazó képünk, akkor olyan képeket kell keresnünk, amik színben vagy alakban hasonlítanak hozzá, a textúra ebben az esetben nem érdekes. Mivel a tulajdonságvektorok két kép összehasonlításában az eltéréseket jelentik, tudjuk, hogy azokat a képeket keressük, ahol a vektorban a színhez és a textúrához tartozó érék kicsi. A szekvencia a következ lehet: {N x 10 }{N z 10 }{N y 100 } 7. Konklúzió A módszerünk, a szomszédsági szekvenciák képadatbázisokban való használata kiterjeszthet további dimenziókra, azaz további tulajdonságok vizsgálatára, és természetesen alkalmazható egyéb alkalmazásokban, ahol tulajdonságok alapján mérhet távolság objektumok között. Az alkalmazásunk Java nyelven íródott, adott képhez a megadott szekvencia alapján a legközelebb es 50-b l egy HTML fájl generál. Futási ideje egy 1GHz-es Pentium-on kb. 1 perc.
6 Irodalomjegyzék [1] P.E. Danielsson, 3D octagonal metrics, Eighth Scandinavian Conf. Image Process., pp , [2] P.P. Das, P.P. Chakrabarti, and B.N. Chatterji, Generalised distances in digital geometry Inform. Sci. 42, pp , [3] A. Fazekas, Lattice of distances based on 3D-neighbourhood sequences, Acta Mathematica Academiae Paedagogicae Nyiregyháziensis 15 (1999), [4] A. Fazekas, A. Hajdu, L. Hajdu, Lattice of generalized neighbourhood sequences in nd and D Publ. Math. Debrecen 60, pp , [5] A. Hajdu and L. Hajdu, Analytical and approximation properties of neighborhood sequences, KÉPAF 4 (2003), Miskolc-Tapolca. [6] A. Hajdu, L. Hajdu, R. Tijdeman, General neighborhood sequences in Z n Discrete Appl. Math., submitted. [7]András Hajdu, János Kormos, Benedek Nagy, Zoltán Zörg : Choosing appropriate distance measurement in digital image segmentation, Annales Univ.Sci. Budapest. Sect. Comp. 24 (2004), [8] A. Hajdu, B. Nagy, Z. Zörg, Indexing and segmenting colour images using neighbourhood sequences, IEEE ICIP 2003, Barcelona, Spain, pp. I/ [9] C. Kiselman, Regularity of distance transformations in image analysis, Computer Vision and Image Understanding 64, pp , [10] J. Kormos, K. Veréb, Recognition of Chain-Coded Patches with Statistical Methods, Mathematical and Computer Modelling, Vol.: 38, 7-9, 2003, [11] Lew, M.S., Principles of Visual Information Retrieval (ed.), Springer, [12] B. Nagy, Distance functions based on neighbourhood sequences, Publicationes Mathematicae Debrecen 63/3 (2003), [13] Oracle intermedia User's Guide and Reference, Release Part Number A , [14] Oracle Visual Information Retrieval User's Guide and Reference, Release 8.1.7, Part No. A , [15] Gy. E. Révész, Introduction To Formal Languages McGraw-Hill Book, Singapore, [16] A. Rosenfeld, and R.A. Melter, Digital geometry The Mathematical Intelligencer 11, pp , [17] A. Rosenfeld, and J.L. Pfaltz, Distance functions on digital pictures Pattern Recognition 1, pp , [18] Santini, S., Exploratory Image Databases Academic Press, [19] M. Yamashita, and T. Ibaraki, Distances defined by neighbourhood sequences Pattern Recognition 19, pp , 1986.
Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások
 Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
optimalizált vizuális adatstruktúra is erőteljesen épít a redundáns vizuális információ veszteséges
 JPEG és fraktál alapú képtömörítő eljárások összehasonlítása és alkalmazási lehetőségei multimédia alapú anyagok fejlesztésénél (Comparison and Using Possibilities of JPEG and Fractal Based Image Compressing
JPEG és fraktál alapú képtömörítő eljárások összehasonlítása és alkalmazási lehetőségei multimédia alapú anyagok fejlesztésénél (Comparison and Using Possibilities of JPEG and Fractal Based Image Compressing
T Ö. Irodalom http://www V Á
 T Ö BB V Á T O Z Ó TAT I Z T I K A Irodalom http://www www.szit.bme.hu/~kela/ind2 - Bolla-Krámli: tatisztikai következések elmélete, Typotex, 2005 - Vargha A.: Matematikai statisztika, Pólya, 2000 - Bryman,
T Ö BB V Á T O Z Ó TAT I Z T I K A Irodalom http://www www.szit.bme.hu/~kela/ind2 - Bolla-Krámli: tatisztikai következések elmélete, Typotex, 2005 - Vargha A.: Matematikai statisztika, Pólya, 2000 - Bryman,
Sztojka Miroszláv LINEÁRIS ALGEBRA Egyetemi jegyzet Ungvár 2013
 UKRAJNA OKTATÁSI ÉS TUDOMÁNYÜGYI MINISZTÉRIUMA ÁLLAMI FELSŐOKTATÁSI INTÉZMÉNY UNGVÁRI NEMZETI EGYETEM MAGYAR TANNYELVŰ HUMÁN- ÉS TERMÉSZETTUDOMÁNYI KAR FIZIKA ÉS MATEMATIKA TANSZÉK Sztojka Miroszláv LINEÁRIS
UKRAJNA OKTATÁSI ÉS TUDOMÁNYÜGYI MINISZTÉRIUMA ÁLLAMI FELSŐOKTATÁSI INTÉZMÉNY UNGVÁRI NEMZETI EGYETEM MAGYAR TANNYELVŰ HUMÁN- ÉS TERMÉSZETTUDOMÁNYI KAR FIZIKA ÉS MATEMATIKA TANSZÉK Sztojka Miroszláv LINEÁRIS
Neme nő Születési dátum 26/10/1988 Állampolgárság magyar
 SZEMÉLYI ADATOK Nagy Noémi Magyarország, 1165 Budapest, Újszász utca 45/B K. ép. I. lph. 3. em. 2. 06 70 340 7335 matnagyn@uni-miskolc.hu http://uni-miskolc.hu/~matnagyn Neme nő Születési dátum 26/10/1988
SZEMÉLYI ADATOK Nagy Noémi Magyarország, 1165 Budapest, Újszász utca 45/B K. ép. I. lph. 3. em. 2. 06 70 340 7335 matnagyn@uni-miskolc.hu http://uni-miskolc.hu/~matnagyn Neme nő Születési dátum 26/10/1988
Informatikai alapképzésben vizsgázó hallgatók eredményei a kreativitás tükrében
 Informatikai alapképzésben vizsgázó hallgatók eredményei a kreativitás tükrében VARGA Andrea Pécsi Tudományegyetem, Természettudományi Kar, Pécs andyka92@gamma.ttk.pte.hu Felmérésem célkitűzése, hogy több
Informatikai alapképzésben vizsgázó hallgatók eredményei a kreativitás tükrében VARGA Andrea Pécsi Tudományegyetem, Természettudományi Kar, Pécs andyka92@gamma.ttk.pte.hu Felmérésem célkitűzése, hogy több
KÉPALKOTÁSRA ALAPOZOTT RUHAIPARI
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR ÍRTA: SZABÓ LAJOS OKLEVELES IPARI TERMÉK- ÉS FORMATERVEZŐ MÉRNÖK KÉPALKOTÁSRA ALAPOZOTT RUHAIPARI MÉRÉSTECHNIKÁK CÍMŰ TÉMAKÖRBŐL, AMELLYEL
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR ÍRTA: SZABÓ LAJOS OKLEVELES IPARI TERMÉK- ÉS FORMATERVEZŐ MÉRNÖK KÉPALKOTÁSRA ALAPOZOTT RUHAIPARI MÉRÉSTECHNIKÁK CÍMŰ TÉMAKÖRBŐL, AMELLYEL
D é n e s T a m á s matematikus-kriptográfus
 D é n e s T a m á s matematikus-kriptográfus e-mail: tdenest@freemail.hu Gondolatok a társadalomkutatás módszertanáról és oktatásáról (Társadalom-holográfia) 1. Elméleti elızmények A társadalomkutatás
D é n e s T a m á s matematikus-kriptográfus e-mail: tdenest@freemail.hu Gondolatok a társadalomkutatás módszertanáról és oktatásáról (Társadalom-holográfia) 1. Elméleti elızmények A társadalomkutatás
Anatómiai régiók automatikus felismerése
 Anatómiai régiók automatikus felismerése Kutatási beszámoló 2015. június Készítette: Tóth Márton József Bevezetés A mai klinikai gyakorlatban a háromdimenziós orvosi képalkotó rendszerek használata igen
Anatómiai régiók automatikus felismerése Kutatási beszámoló 2015. június Készítette: Tóth Márton József Bevezetés A mai klinikai gyakorlatban a háromdimenziós orvosi képalkotó rendszerek használata igen
ENCARNACAO, J.L. PEITGEN, H.-O. SAKAS, G. ENGLERT, G. editors (1992): Fractal Geometry and Computer Graphics, Springer- Verlag, Berlin Heidelberg. EAR
 Irodalomjegyzék ACM Multimedia'95 Proceedings, (1995): Addison-Wesley Publishing Company, ACM Press, USA. ADOBE Photoshop 4.0 User Guide for Macintosh and Windows. ADOBE Photoshop 3.5 User Guide for UNIX.
Irodalomjegyzék ACM Multimedia'95 Proceedings, (1995): Addison-Wesley Publishing Company, ACM Press, USA. ADOBE Photoshop 4.0 User Guide for Macintosh and Windows. ADOBE Photoshop 3.5 User Guide for UNIX.
ERserver. iseries. Szolgáltatási minőség
 ERserver iseries Szolgáltatási minőség ERserver iseries Szolgáltatási minőség Szerzői jog IBM Corporation 2002. Minden jog fenntartva Tartalom Szolgáltatási minőség (QoS)............................ 1
ERserver iseries Szolgáltatási minőség ERserver iseries Szolgáltatási minőség Szerzői jog IBM Corporation 2002. Minden jog fenntartva Tartalom Szolgáltatási minőség (QoS)............................ 1
Tartalom. Descartes-koordináták. Geometriai értelmezés. Pont. Egyenes. Klár Gergely tremere@elte.hu. 2010/2011. tavaszi félév
 Tartalom Pont Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar Egyenes Sík Háromszög Gömb 2010/2011. tavaszi félév Descartes-koordináták Geometriai értelmezés
Tartalom Pont Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar Egyenes Sík Háromszög Gömb 2010/2011. tavaszi félév Descartes-koordináták Geometriai értelmezés
Hazánkban jelentõs múlttal rendelkeznek a klasszikus tesztelméleti módszerekkel
 Iskolakultúra 2008/1 2 Molnár Gyöngyvér SZTE, Pedagógia Tanszék, MTA-SZTE Képességkutató Csoport A Rasch-modell kiterjesztése nem dichotóm adatok elemzésére: a rangskálás és a parciális kredit modell A
Iskolakultúra 2008/1 2 Molnár Gyöngyvér SZTE, Pedagógia Tanszék, MTA-SZTE Képességkutató Csoport A Rasch-modell kiterjesztése nem dichotóm adatok elemzésére: a rangskálás és a parciális kredit modell A
E-LEARNING ALAPÚ TÁVOKTATÁS A SZÉCHENYI ISTVÁN EGYETEMEN
 E-LEARNING ALAPÚ TÁVOKTATÁS A SZÉCHENYI ISTVÁN EGYETEMEN E-LEARNING BASED DISTANCE EDUCATION AT SZÉCHENYI ISTVÁN UNIVERSITY Nyéki Lajos, nyeki@sze.hu Széchenyi István Egyetem 1. Bevezetés A Széchenyi István
E-LEARNING ALAPÚ TÁVOKTATÁS A SZÉCHENYI ISTVÁN EGYETEMEN E-LEARNING BASED DISTANCE EDUCATION AT SZÉCHENYI ISTVÁN UNIVERSITY Nyéki Lajos, nyeki@sze.hu Széchenyi István Egyetem 1. Bevezetés A Széchenyi István
SZAKKÉPZÉSI KERETTANTERV a(z) 55 213 05 MULTIMÉDIA-ALMAZÁSFEJLESZTŐ SZAKKÉPESÍTÉS-RÁÉPÜLÉSHEZ
 SZAKKÉPZÉSI KERETTANTERV a(z) 55 213 05 MULTIMÉDIA-ALMAZÁSFEJLESZTŐ SZAKKÉPESÍTÉS-RÁÉPÜLÉSHEZ I. A szakképzés jogi háttere A szakképzési kerettanterv a nemzeti köznevelésről szóló 2011. évi CXC. törvény,
SZAKKÉPZÉSI KERETTANTERV a(z) 55 213 05 MULTIMÉDIA-ALMAZÁSFEJLESZTŐ SZAKKÉPESÍTÉS-RÁÉPÜLÉSHEZ I. A szakképzés jogi háttere A szakképzési kerettanterv a nemzeti köznevelésről szóló 2011. évi CXC. törvény,
A hierarchikus adatbázis struktúra jellemzői
 A hierarchikus adatbázis struktúra jellemzői Az első adatbázis-kezelő rendszerek a hierarchikus modellen alapultak. Ennek az volt a magyarázata, hogy az élet sok területén első közelítésben elég jól lehet
A hierarchikus adatbázis struktúra jellemzői Az első adatbázis-kezelő rendszerek a hierarchikus modellen alapultak. Ennek az volt a magyarázata, hogy az élet sok területén első közelítésben elég jól lehet
2. Halmazelmélet (megoldások)
 (megoldások) 1. A pozitív háromjegy páros számok halmaza. 2. Az olyan, 3-mal osztható egész számok halmaza, amelyek ( 100)-nál nagyobbak és 100-nál kisebbek. 3. Az olyan pozitív egész számok halmaza, amelyeknek
(megoldások) 1. A pozitív háromjegy páros számok halmaza. 2. Az olyan, 3-mal osztható egész számok halmaza, amelyek ( 100)-nál nagyobbak és 100-nál kisebbek. 3. Az olyan pozitív egész számok halmaza, amelyeknek
A rádióelektronikai háború új eszközei: a széttelepített rádiólokátor
 A rádióelektronikai háború új eszközei: a széttelepített rádiólokátor DR. SERES GYÖRGY mérnök alezredes, a hadtudományok (haditechnika) kandidátusa A korszerű rádióelektronikai harc egyik nagy dilemmája:
A rádióelektronikai háború új eszközei: a széttelepített rádiólokátor DR. SERES GYÖRGY mérnök alezredes, a hadtudományok (haditechnika) kandidátusa A korszerű rádióelektronikai harc egyik nagy dilemmája:
Tervezett erdőgazdálkodási tevékenységek bejelentése
 Tervezett erdőgazdálkodási tevékenységek bejelentése ERDŐGAZDÁLKODÁSI HATÓSÁGI BEJELENTÉSEK/ TERVEZETT ERDŐGAZDÁLKODÁSI TEV. BEJELENTÉSE A Tervezett erdőgazdálkodási tevékenységek bejelentése a fakitermelési
Tervezett erdőgazdálkodási tevékenységek bejelentése ERDŐGAZDÁLKODÁSI HATÓSÁGI BEJELENTÉSEK/ TERVEZETT ERDŐGAZDÁLKODÁSI TEV. BEJELENTÉSE A Tervezett erdőgazdálkodási tevékenységek bejelentése a fakitermelési
Dr. Pétery Kristóf: AutoCAD LT 2002 Blokkok, Xrefek
 2 Minden jog fenntartva, beleértve bárminemű sokszorosítás, másolás és közlés jogát is. Kiadja a Mercator Stúdió Felelős kiadó a Mercator Stúdió vezetője Lektor: Gál Veronika Szerkesztő: Pétery István
2 Minden jog fenntartva, beleértve bárminemű sokszorosítás, másolás és közlés jogát is. Kiadja a Mercator Stúdió Felelős kiadó a Mercator Stúdió vezetője Lektor: Gál Veronika Szerkesztő: Pétery István
VALÓS HULLÁMFRONT ELŐÁLLÍTÁSA A SZÁMÍTÓGÉPES ÉS A DIGITÁLIS HOLOGRÁFIÁBAN PhD tézisfüzet
 VALÓS HULLÁMFRONT ELŐÁLLÍTÁSA A SZÁMÍTÓGÉPES ÉS A DIGITÁLIS HOLOGRÁFIÁBAN PhD tézisfüzet PAPP ZSOLT Budapesti Műszaki és Gazdaságtudományi Egyetem Fizika Tanszék 2003 1 Bevezetés A lézerek megjelenését
VALÓS HULLÁMFRONT ELŐÁLLÍTÁSA A SZÁMÍTÓGÉPES ÉS A DIGITÁLIS HOLOGRÁFIÁBAN PhD tézisfüzet PAPP ZSOLT Budapesti Műszaki és Gazdaságtudományi Egyetem Fizika Tanszék 2003 1 Bevezetés A lézerek megjelenését
A DIGITÁLIS KÉPFELDOLGOZÁS TERÜLETÉN FOLYÓ KUTATÁSOK A DEBRECENI EGYETEM INFORMATIKAI KARÁN
 A DIGITÁLIS KÉPFELDOLGOZÁS TERÜLETÉN FOLYÓ KUTATÁSOK A DEBRECENI EGYETEM INFORMATIKAI KARÁN RESEARCH ON DIGITAL IMAGE PROCESSING AT FACULTY OF INFORMATICS, UNIVERSITY OF DEBRECEN Fazekas Attila, Hajdu
A DIGITÁLIS KÉPFELDOLGOZÁS TERÜLETÉN FOLYÓ KUTATÁSOK A DEBRECENI EGYETEM INFORMATIKAI KARÁN RESEARCH ON DIGITAL IMAGE PROCESSING AT FACULTY OF INFORMATICS, UNIVERSITY OF DEBRECEN Fazekas Attila, Hajdu
VI. Magyar Földrajzi Konferencia 524-529
 Van Leeuwen Boudewijn Tobak Zalán Szatmári József 1 BELVÍZ OSZTÁLYOZÁS HAGYOMÁNYOS MÓDSZERREL ÉS MESTERSÉGES NEURÁLIS HÁLÓVAL BEVEZETÉS Magyarország, különösen pedig az Alföld váltakozva szenved aszályos
Van Leeuwen Boudewijn Tobak Zalán Szatmári József 1 BELVÍZ OSZTÁLYOZÁS HAGYOMÁNYOS MÓDSZERREL ÉS MESTERSÉGES NEURÁLIS HÁLÓVAL BEVEZETÉS Magyarország, különösen pedig az Alföld váltakozva szenved aszályos
A DIGITÁLIS KÉPFELDOLGOZÁS OKTATÁSÁNAK EREDMÉNYEI ÉS NÉHÁNY AKTUÁLIS KÉRDÉSE A DEBRECENI EGYETEMEN
 A DIGITÁLIS KÉPFELDOLGOZÁS OKTATÁSÁNAK EREDMÉNYEI ÉS NÉHÁNY AKTUÁLIS KÉRDÉSE A DEBRECENI EGYETEMEN CURRENT QUESTIONS AND RESULTS ABOUT THE EDUCATION OF DIGITAL IMAGE PROCESSING AT THE UNIVERSITY OF DEBRECEN
A DIGITÁLIS KÉPFELDOLGOZÁS OKTATÁSÁNAK EREDMÉNYEI ÉS NÉHÁNY AKTUÁLIS KÉRDÉSE A DEBRECENI EGYETEMEN CURRENT QUESTIONS AND RESULTS ABOUT THE EDUCATION OF DIGITAL IMAGE PROCESSING AT THE UNIVERSITY OF DEBRECEN
TÁMOP 4.1.1 VIR alprojekt VIR felhasználói kézikönyv
 1. sz. melléklet TÁMOP 4.1.1 VIR alprojekt Készítette: Aloha Informatika Kft. Tartalomjegyzék 1. A Vezetői Információs Rendszer, mint a stratégiai gondolkodás eszköze...4 1.1 Elméleti háttér...4 1.2 VIR
1. sz. melléklet TÁMOP 4.1.1 VIR alprojekt Készítette: Aloha Informatika Kft. Tartalomjegyzék 1. A Vezetői Információs Rendszer, mint a stratégiai gondolkodás eszköze...4 1.1 Elméleti háttér...4 1.2 VIR
A képfeldolgozás matematikája I.
 1 A képfeldolgozás matematikája I. Bevezetés Dr. Fazekas Attila Attila.Fazekas@inf.unideb.hu Polányi Mihály: A személyes tudás A sikeres kommunikáció kedvéért az üzenet feladója 2 Polányi Mihály: A személyes
1 A képfeldolgozás matematikája I. Bevezetés Dr. Fazekas Attila Attila.Fazekas@inf.unideb.hu Polányi Mihály: A személyes tudás A sikeres kommunikáció kedvéért az üzenet feladója 2 Polányi Mihály: A személyes
KÉPI INFORMÁCIÓK KEZELHETŐSÉGE. Forczek Erzsébet SZTE ÁOK Orvosi Informatikai Intézet. Összefoglaló
 KÉPI INFORMÁCIÓK KEZELHETŐSÉGE Forczek Erzsébet SZTE ÁOK Orvosi Informatikai Intézet Összefoglaló Tanórákon és az önálló tanulás részeként is, az informatika világában a rendelkezésünkre álló óriási mennyiségű
KÉPI INFORMÁCIÓK KEZELHETŐSÉGE Forczek Erzsébet SZTE ÁOK Orvosi Informatikai Intézet Összefoglaló Tanórákon és az önálló tanulás részeként is, az informatika világában a rendelkezésünkre álló óriási mennyiségű
FERROMÁGNESES ANYAGOK RONCSOLÁSMENTES VIZSGÁLATA MÁGNESESHISZTERÉZIS-ALHURKOK MÉRÉSE ALAPJÁN. Mágneses adaptív teszt (MAT) Vértesy Gábor
 FERROMÁGNESES ANYAGOK RONCSOLÁSMENTES VIZSGÁLATA MÁGNESESHISZTERÉZIS-ALHURKOK Vértesy Gábor MÉRÉSE ALAPJÁN MTA TTK Műszaki Fizikai és Anyagtudományi Intézet Olyan új, gyorsan elvégezhetô, megbízható és
FERROMÁGNESES ANYAGOK RONCSOLÁSMENTES VIZSGÁLATA MÁGNESESHISZTERÉZIS-ALHURKOK Vértesy Gábor MÉRÉSE ALAPJÁN MTA TTK Műszaki Fizikai és Anyagtudományi Intézet Olyan új, gyorsan elvégezhetô, megbízható és
Közlekedési események képi feldolgozása
 Közlekedési események képi feldolgozása Max Gyula Budapest Műszaki és Gazdaságtudományi Egyetem, Automatizálási és Alkalmazott Informatikai Tanszék 1521 Budapest, Pf. 91, { e-mail: max@aut.bme.hu} Abstract.
Közlekedési események képi feldolgozása Max Gyula Budapest Műszaki és Gazdaságtudományi Egyetem, Automatizálási és Alkalmazott Informatikai Tanszék 1521 Budapest, Pf. 91, { e-mail: max@aut.bme.hu} Abstract.
Doktori PhD értekezés
 Doktori PhD értekezés Békési Bertold 2006 ZRÍNYI MIKLÓS NEMZETVÉDELMI EGYETEM BOLYAI JÁNOS KATONAI MŰSZAKI KAR KATONAI MŰSZAKI DOKTORI ISKOLA Békési Bertold okl. mk. őrnagy A KATONAI REPÜLŐGÉPEK ÜZEMELTETÉSÉNEK,
Doktori PhD értekezés Békési Bertold 2006 ZRÍNYI MIKLÓS NEMZETVÉDELMI EGYETEM BOLYAI JÁNOS KATONAI MŰSZAKI KAR KATONAI MŰSZAKI DOKTORI ISKOLA Békési Bertold okl. mk. őrnagy A KATONAI REPÜLŐGÉPEK ÜZEMELTETÉSÉNEK,
Aronic Főkönyv kettős könyvviteli programrendszer
 6085 Fülöpszállás, Kiskunság tér 4. Internet: www.cin.hu E-mail: software@cin.hu Tel: 78/435-081, 30/9-573-673, 30/9-593-167 kettős könyvviteli programrendszer v2.0 Szoftverdokumentáció Önnek is jár egy
6085 Fülöpszállás, Kiskunság tér 4. Internet: www.cin.hu E-mail: software@cin.hu Tel: 78/435-081, 30/9-573-673, 30/9-593-167 kettős könyvviteli programrendszer v2.0 Szoftverdokumentáció Önnek is jár egy
Újdonságok. Release 2
 ARCHLine.XP 2009 Windows Újdonságok Release 2 A dokumentációban levı anyag változásának jogát a CadLine Kft fenntartja, ennek bejelentésére kötelezettséget nem vállal. A szoftver, ami tartalmazza az ebben
ARCHLine.XP 2009 Windows Újdonságok Release 2 A dokumentációban levı anyag változásának jogát a CadLine Kft fenntartja, ennek bejelentésére kötelezettséget nem vállal. A szoftver, ami tartalmazza az ebben
Stratégiai menedzsment
 Fülöp Gyula Stratégiai menedzsment Elmélet és gyakorlat Perfekt Kiadó Tartalom Bevezetés... 9 1. A stratégia lényege, stratégiai alapfogalmak... 11 1.1. Katonai gyökerek... 11 1.2. Stratégia az üzleti
Fülöp Gyula Stratégiai menedzsment Elmélet és gyakorlat Perfekt Kiadó Tartalom Bevezetés... 9 1. A stratégia lényege, stratégiai alapfogalmak... 11 1.1. Katonai gyökerek... 11 1.2. Stratégia az üzleti
4. LECKE: DÖNTÉSI FÁK - OSZTÁLYOZÁS II. -- Előadás. 4.1. Döntési fák [Concepts Chapter 11]
![4. LECKE: DÖNTÉSI FÁK - OSZTÁLYOZÁS II. -- Előadás. 4.1. Döntési fák [Concepts Chapter 11] 4. LECKE: DÖNTÉSI FÁK - OSZTÁLYOZÁS II. -- Előadás. 4.1. Döntési fák [Concepts Chapter 11]](/thumbs/34/17147027.jpg) 1 4. LECKE: DÖNTÉSI FÁK - OSZTÁLYOZÁS II. -- Előadás 4.1. Döntési fák [Concepts Chapter 11] A döntési fákon alapuló klasszifikációs eljárás nagy előnye, hogy az alkalmazása révén nemcsak egyedenkénti előrejelzést
1 4. LECKE: DÖNTÉSI FÁK - OSZTÁLYOZÁS II. -- Előadás 4.1. Döntési fák [Concepts Chapter 11] A döntési fákon alapuló klasszifikációs eljárás nagy előnye, hogy az alkalmazása révén nemcsak egyedenkénti előrejelzést
1 Rendszer alapok. 1.1 Alapfogalmak
 ÉRTÉKTEREMTŐ FOLYAM ATOK MENEDZSMENTJE II. RENDSZEREK ÉS FOLYAMATOK TARTALOMJEGYZÉK 1 Rendszer alapok 1.1 Alapfogalmak 1.2 A rendszerek csoportosítása 1.3 Rendszerek működése 1.4 Rendszerek leírása, modellezése,
ÉRTÉKTEREMTŐ FOLYAM ATOK MENEDZSMENTJE II. RENDSZEREK ÉS FOLYAMATOK TARTALOMJEGYZÉK 1 Rendszer alapok 1.1 Alapfogalmak 1.2 A rendszerek csoportosítása 1.3 Rendszerek működése 1.4 Rendszerek leírása, modellezése,
Fókuszált fénynyalábok keresztpolarizációs jelenségei
 Fókuszált fénynyalábok keresztpolarizációs jelenségei K házi-kis Ambrus, Klebniczki József Kecskeméti F iskola GAMF Kar Matematika és Fizika Tanszék, 6000 Kecskemét, Izsáki út 10. Véges transzverzális
Fókuszált fénynyalábok keresztpolarizációs jelenségei K házi-kis Ambrus, Klebniczki József Kecskeméti F iskola GAMF Kar Matematika és Fizika Tanszék, 6000 Kecskemét, Izsáki út 10. Véges transzverzális
FELHASZNÁLÓI LEÍRÁS a DIMSQL Integrált Számviteli Rendszer Készlet moduljának használatához
 FELHASZNÁLÓI LEÍRÁS a DIMSQL Integrált Számviteli Rendszer Készlet moduljának használatához - 1 - www.dimenzio-kft.hu Tartalomjegyzék A. BEVEZETÉS... 4 I. BEÁLLÍTÁSOK, PARAMÉTEREK, NAPLÓFORMÁTUMOK... 4
FELHASZNÁLÓI LEÍRÁS a DIMSQL Integrált Számviteli Rendszer Készlet moduljának használatához - 1 - www.dimenzio-kft.hu Tartalomjegyzék A. BEVEZETÉS... 4 I. BEÁLLÍTÁSOK, PARAMÉTEREK, NAPLÓFORMÁTUMOK... 4
4. sz. Füzet. A hibafa számszerű kiértékelése 2002.
 M Ű S Z A K I B I Z O N S Á G I F Ő F E L Ü G Y E L E 4. sz. Füzet A hibafa számszerű kiértékelése 00. Sem a Műszaki Biztonsági Főfelügyelet, sem annak nevében, képviseletében vagy részéről eljáró személy
M Ű S Z A K I B I Z O N S Á G I F Ő F E L Ü G Y E L E 4. sz. Füzet A hibafa számszerű kiértékelése 00. Sem a Műszaki Biztonsági Főfelügyelet, sem annak nevében, képviseletében vagy részéről eljáró személy
A Debreceni Egyetem és a Nagyváradi Egyetem WiFi alapú helymeghatározó rendszere
 A Debreceni Egyetem és a Nagyváradi Egyetem WiFi alapú helymeghatározó rendszere Gál Zoltán 1 Marius Onic 2 1 IT igazgató, Debreceni Egyetem TEK, zgal@unideb.hu 2 IT vezet, Nagyváradi Egyetem, omar@uoradea.ro
A Debreceni Egyetem és a Nagyváradi Egyetem WiFi alapú helymeghatározó rendszere Gál Zoltán 1 Marius Onic 2 1 IT igazgató, Debreceni Egyetem TEK, zgal@unideb.hu 2 IT vezet, Nagyváradi Egyetem, omar@uoradea.ro
Önálló laboratórium beszámoló
 Önálló laboratórium beszámoló BME-TMIT Készítette: Sümeghy Tamás Pál Neptun-kód: GFHSRE Szak: műszaki informatikus Szakirány: Internet és infokommunikációs alkalmazásai E-mail cím: schumy@sch.bme.hu Konzulens(ek):
Önálló laboratórium beszámoló BME-TMIT Készítette: Sümeghy Tamás Pál Neptun-kód: GFHSRE Szak: műszaki informatikus Szakirány: Internet és infokommunikációs alkalmazásai E-mail cím: schumy@sch.bme.hu Konzulens(ek):
Csigatisztítók hatékonyságának minősítési módszere
 Csigatisztítók hatékonyságának minősítési módszere Török Dániel, Suplicz András, Kovács József Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem, Gépészmérnöki Kar, Polimertechnika Tanszék, Műegyetem
Csigatisztítók hatékonyságának minősítési módszere Török Dániel, Suplicz András, Kovács József Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem, Gépészmérnöki Kar, Polimertechnika Tanszék, Műegyetem
MATEMATIKA. 5 8. évfolyam
 MATEMATIKA 5 8. évfolyam Célok és feladatok A matematikatanítás célja és ennek kapcsán feladata: megismertetni a tanulókat az őket körülvevő konkrét környezet mennyiségi és térbeli viszonyaival, megalapozni
MATEMATIKA 5 8. évfolyam Célok és feladatok A matematikatanítás célja és ennek kapcsán feladata: megismertetni a tanulókat az őket körülvevő konkrét környezet mennyiségi és térbeli viszonyaival, megalapozni
Gazdasági informatika vizsga kérdések
 Gazdasági informatika vizsga kérdések 1. Mi az adatbázis? Adatbázisnak a valós világ egy részhalmazának leírásához használt adatok összefüggı, rendezett halmazát nevezzük. 2. Mit az adatbázis-kezelı rendszer?
Gazdasági informatika vizsga kérdések 1. Mi az adatbázis? Adatbázisnak a valós világ egy részhalmazának leírásához használt adatok összefüggı, rendezett halmazát nevezzük. 2. Mit az adatbázis-kezelı rendszer?
Online kérd íves felmérés a Gazdálkodás olvasóinak és szerz inek körében
 389 V ITA Online kérd íves felmérés a Gazdálkodás olvasóinak és szerz inek körében FEHÉR ANDRÁS SZABÓ G. GÁBOR SZAKÁLY ZOLTÁN Kulcsszavak: elégedettség, vélemények, olvasók, szerz k, Gazdálkodás. ÖSSZEFOGLALÓ
389 V ITA Online kérd íves felmérés a Gazdálkodás olvasóinak és szerz inek körében FEHÉR ANDRÁS SZABÓ G. GÁBOR SZAKÁLY ZOLTÁN Kulcsszavak: elégedettség, vélemények, olvasók, szerz k, Gazdálkodás. ÖSSZEFOGLALÓ
Diplomamunka. Koczka László
 Diplomamunka Koczka László Debrecen 010 Debreceni Egyetem Informatikai Kar Közgazdasági Modellek Számítógépes Szimulációja Témavezető: Dr. Földvári Péter Egyetemi adjunktus Készítette: Koczka László Gazdaságinformatikus
Diplomamunka Koczka László Debrecen 010 Debreceni Egyetem Informatikai Kar Közgazdasági Modellek Számítógépes Szimulációja Témavezető: Dr. Földvári Péter Egyetemi adjunktus Készítette: Koczka László Gazdaságinformatikus
Készítette: niethammer@freemail.hu
 VLogo VRML generáló program Készítette: Niethammer Zoltán niethammer@freemail.hu 2008 Bevezetés A VLogo az általános iskolákban használt Comenius Logo logikájára épülő programozási nyelv. A végeredmény
VLogo VRML generáló program Készítette: Niethammer Zoltán niethammer@freemail.hu 2008 Bevezetés A VLogo az általános iskolákban használt Comenius Logo logikájára épülő programozási nyelv. A végeredmény
Mátrixaritmetika. Tartalom:
 Mátrixaritmetika Tartalom: A vektor és mátrix fogalma Speciális mátrixok Relációk és műveletek mátrixokkal A mátrixok szorzása A diadikus szorzat. Hatványozás Gyakorlati alkalmazások Készítette: Dr. Ábrahám
Mátrixaritmetika Tartalom: A vektor és mátrix fogalma Speciális mátrixok Relációk és műveletek mátrixokkal A mátrixok szorzása A diadikus szorzat. Hatványozás Gyakorlati alkalmazások Készítette: Dr. Ábrahám
A HEVES-BORSODI-DOMBSÁG MORFOMETRIAI ELEMZÉSE TÉRINFORMATIKAI MÓDSZEREKKEL. Utasi Zoltán 1. A terület elhelyezkedése
 Földrajz Konferencia, Szeged 2001. A HEVES-BORSODI-DOMBSÁG MORFOMETRIAI ELEMZÉSE TÉRINFORMATIKAI MÓDSZEREKKEL Utasi Zoltán 1 A terület elhelyezkedése A Heves-Borsodi-dombság a Mátra és a Bükk vonulatától
Földrajz Konferencia, Szeged 2001. A HEVES-BORSODI-DOMBSÁG MORFOMETRIAI ELEMZÉSE TÉRINFORMATIKAI MÓDSZEREKKEL Utasi Zoltán 1 A terület elhelyezkedése A Heves-Borsodi-dombság a Mátra és a Bükk vonulatától
Széchenyi István Szakképző Iskola
 A SZAKKÖZÉPISKOLAI SZAKMACSOPORTOS ALAPOZÓ OKTATÁS EMELT SZINTŰ ISKOLAI PROGRAMJA 11-12. évolyam Érvényes a 2003-2004-es tanévtől felmenő rendszerben Átdolgozva, utolsó módosítás: 2004. április 26. Az
A SZAKKÖZÉPISKOLAI SZAKMACSOPORTOS ALAPOZÓ OKTATÁS EMELT SZINTŰ ISKOLAI PROGRAMJA 11-12. évolyam Érvényes a 2003-2004-es tanévtől felmenő rendszerben Átdolgozva, utolsó módosítás: 2004. április 26. Az
INFORMATIKA HELYI TANTERV
 INFORMATIKA HELYI TANTERV Az alsó tagozatos informatikai fejlesztés során törekedni kell a témához kapcsolódó korosztálynak megfelelő használatára, az informatikai eszközök működésének bemutatására, megértésére
INFORMATIKA HELYI TANTERV Az alsó tagozatos informatikai fejlesztés során törekedni kell a témához kapcsolódó korosztálynak megfelelő használatára, az informatikai eszközök működésének bemutatására, megértésére
Optikai karakterfelismerés
 Optikai karakterfelismerés Az optikai karakterfelismerés feladata A különböző formátumú dokumentumok kezelésének egyik speciális esete, amikor a kezelendő dokumentumok még nem állnak rendelkezésre elektronikus
Optikai karakterfelismerés Az optikai karakterfelismerés feladata A különböző formátumú dokumentumok kezelésének egyik speciális esete, amikor a kezelendő dokumentumok még nem állnak rendelkezésre elektronikus
Mérési sorozatok tanulságai
 Kovács Tibor - Reményi Tibor Mérési sorozatok tanulságai A cikkben olyan valós eszközökkel ténylegesen végrehajtott mérési sorozatokat mutatunk be, amelyek arra szolgálhatnak, hogy helyesen vegyük fel
Kovács Tibor - Reményi Tibor Mérési sorozatok tanulságai A cikkben olyan valós eszközökkel ténylegesen végrehajtott mérési sorozatokat mutatunk be, amelyek arra szolgálhatnak, hogy helyesen vegyük fel
Diagnosztikai szemléletű talajtérképek szerkesztése korrelált talajtani adatrendszerek alapján
 Diagnosztikai szemléletű talajtérképek szerkesztése korrelált talajtani adatrendszerek alapján Bakacsi Zsófia 1 - Szabó József 1 Waltner István 2 Michéli Erika 2 Fuchs Márta 2 - Laborczi Annamária 1 -
Diagnosztikai szemléletű talajtérképek szerkesztése korrelált talajtani adatrendszerek alapján Bakacsi Zsófia 1 - Szabó József 1 Waltner István 2 Michéli Erika 2 Fuchs Márta 2 - Laborczi Annamária 1 -
PONTASÍTÁSOK a 2015/S 126-230625 számú közbeszerzés belvízi csatorna-modellek előállítására vonatkozó Műszaki Dokumentációjához
 PONTASÍTÁSOK a 2015/S 126-230625 számú közbeszerzés belvízi csatorna-modellek előállítására vonatkozó Műszaki Dokumentációjához A dokumentum célja Jelen dokumentum a 2015/S 126-230625 számú közbeszerzési
PONTASÍTÁSOK a 2015/S 126-230625 számú közbeszerzés belvízi csatorna-modellek előállítására vonatkozó Műszaki Dokumentációjához A dokumentum célja Jelen dokumentum a 2015/S 126-230625 számú közbeszerzési
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 9 IX MÁTRIxOk 1 MÁTRIx FOGALmA, TULAJDONSÁGAI A mátrix egy téglalap alakú táblázat, melyben az adatok, a mátrix elemei, sorokban és oszlopokban vannak elhelyezve Az (1) mátrixnak
KOVÁCS BÉLA, MATEmATIkA I 9 IX MÁTRIxOk 1 MÁTRIx FOGALmA, TULAJDONSÁGAI A mátrix egy téglalap alakú táblázat, melyben az adatok, a mátrix elemei, sorokban és oszlopokban vannak elhelyezve Az (1) mátrixnak
kontroll környezetet folyamatokat és a folyamatgazdákat; célkitűzéseit; belső ellenőrzési Általános felmérés: külső és belső kontroll környezetének
 PÁTY KÖZSÉG ÖNKORMÁNYZATA STRATÉGIAI BELSŐ ELLENŐRZÉSI TERVE 2014-2018 Készítette: Majláth Konrád Konstantin okl. pénzügyi adó - pénzügyi ellenőrzési szakértő, költségvetési gazdasági szakértő, közbeszerzési
PÁTY KÖZSÉG ÖNKORMÁNYZATA STRATÉGIAI BELSŐ ELLENŐRZÉSI TERVE 2014-2018 Készítette: Majláth Konrád Konstantin okl. pénzügyi adó - pénzügyi ellenőrzési szakértő, költségvetési gazdasági szakértő, közbeszerzési
Bevezetés. Párhuzamos vetítés és tulajdonságai
 Bevezetés Az ábrázoló geometria célja a háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelműen és egyértelműen visszaállítható (rekonstruálható) módon történő való
Bevezetés Az ábrázoló geometria célja a háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelműen és egyértelműen visszaállítható (rekonstruálható) módon történő való
Brooklyn Credit Risk Monitoring System
 Brooklyn Credit Risk Monitoring System Mi a célja, küldetése a rendszernek Az egyébként kényszerű adatszolgáltatási kötelezettség adatáramára építve olyan rendszer biztosítása, amely 1. Lényegi (mat.stat.)
Brooklyn Credit Risk Monitoring System Mi a célja, küldetése a rendszernek Az egyébként kényszerű adatszolgáltatási kötelezettség adatáramára építve olyan rendszer biztosítása, amely 1. Lényegi (mat.stat.)
J/55. B E S Z Á M O L Ó
 KÖZBESZERZÉSEK TANÁCSA J/55. B E S Z Á M O L Ó az Országgyűlés részére a Közbeszerzések Tanácsának a közbeszerzések tisztaságával és átláthatóságával kapcsolatos tapasztalatairól, valamint a 2005. január
KÖZBESZERZÉSEK TANÁCSA J/55. B E S Z Á M O L Ó az Országgyűlés részére a Közbeszerzések Tanácsának a közbeszerzések tisztaságával és átláthatóságával kapcsolatos tapasztalatairól, valamint a 2005. január
A DRHE MARÓTHI GYÖRGY KÖNYVTÁR SZERVEZETI ÉS MŰKÖDÉSI SZABÁLYZATA
 A DEBRECENI REFORMÁTUS HITTUDOMÁNYI EGYETEM SZERVEZETI ÉS MŰKÖDÉSI SZABÁLYZATÁNAK Ikt. szám: 1425/1300/19-2/2014. 13/B. SZ. MELLÉKLETE A DRHE MARÓTHI GYÖRGY KÖNYVTÁR SZERVEZETI ÉS MŰKÖDÉSI SZABÁLYZATA
A DEBRECENI REFORMÁTUS HITTUDOMÁNYI EGYETEM SZERVEZETI ÉS MŰKÖDÉSI SZABÁLYZATÁNAK Ikt. szám: 1425/1300/19-2/2014. 13/B. SZ. MELLÉKLETE A DRHE MARÓTHI GYÖRGY KÖNYVTÁR SZERVEZETI ÉS MŰKÖDÉSI SZABÁLYZATA
Irinyi József Általános Iskola 4274 Hosszúpályi Szabadság tér 30. 031154. HELYI TANTERV Informatika 4. osztály 2013
 Irinyi József Általános Iskola 4274 Hosszúpályi Szabadság tér 30. 031154 HELYI TANTERV Informatika 4. osztály 2013 Informatika az általános iskola 4. évfolyama számára (heti 1 órás változat) Az alsó tagozatos
Irinyi József Általános Iskola 4274 Hosszúpályi Szabadság tér 30. 031154 HELYI TANTERV Informatika 4. osztály 2013 Informatika az általános iskola 4. évfolyama számára (heti 1 órás változat) Az alsó tagozatos
elektronmikroszkóppal
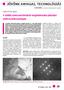 JÖVÕNK ANYAGAI, TECHNOLÓGIÁI ROVATVEZETÕK: dr. Buzáné dr. Dénes Margit és dr. Klug Ottó SZABÓ PÉTER JÁNOS A lokális szemcseorientáció meghatározása pásztázó elektronmikroszkóppal A pásztázó elektronmikroszkópos
JÖVÕNK ANYAGAI, TECHNOLÓGIÁI ROVATVEZETÕK: dr. Buzáné dr. Dénes Margit és dr. Klug Ottó SZABÓ PÉTER JÁNOS A lokális szemcseorientáció meghatározása pásztázó elektronmikroszkóppal A pásztázó elektronmikroszkópos
VEZETÉS- ÉS SZERVEZÉSTUDOMÁNYI PROGRAM KÖTELEZİEN VÁLASZTHATÓ TANTÁRGYAI
 VEZETÉS- ÉS SZERVEZÉSTUDOMÁNYI PROGRAM KÖTELEZİEN VÁLASZTHATÓ TANTÁRGYAI TANTÁRGYI TEMATIKA ÉS KÖVETELMÉNYRENDSZER Tantárgy: neve (magyar) Vezetés- szervezéselmélet és vizsgálati módszerei neve (angol)
VEZETÉS- ÉS SZERVEZÉSTUDOMÁNYI PROGRAM KÖTELEZİEN VÁLASZTHATÓ TANTÁRGYAI TANTÁRGYI TEMATIKA ÉS KÖVETELMÉNYRENDSZER Tantárgy: neve (magyar) Vezetés- szervezéselmélet és vizsgálati módszerei neve (angol)
Matematikai és matematikai statisztikai alapismeretek
 Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
A.26. Hagyományos és korszerű tervezési eljárások
 A.26. Hagyományos és korszerű tervezési eljárások A.26.1. Hagyományos tervezési eljárások A.26.1.1. Csuklós és merev kapcsolatú keretek tervezése Napjainkig a magasépítési tartószerkezetek tervezése a
A.26. Hagyományos és korszerű tervezési eljárások A.26.1. Hagyományos tervezési eljárások A.26.1.1. Csuklós és merev kapcsolatú keretek tervezése Napjainkig a magasépítési tartószerkezetek tervezése a
Veszteséges képtömörítő eljárások pszichovizuális összehasonlítása
 Veszteséges képtömörítő eljárások pszichovizuális összehasonlítása Berke József 1 - Kocsis Péter 2 - Kovács József 2 1 - Pannon Agrártudományi Egyetem, Georgikon, Mezőgazdaságtudományi Kar, Szaktanácsadási,
Veszteséges képtömörítő eljárások pszichovizuális összehasonlítása Berke József 1 - Kocsis Péter 2 - Kovács József 2 1 - Pannon Agrártudományi Egyetem, Georgikon, Mezőgazdaságtudományi Kar, Szaktanácsadási,
A controlling integrálódása az oktatási szférában
 Dr. Tóth Antal - Dr. Zéman Zoltán A controlling integrálódása az oktatási szférában 1. CONTROLLING ALKALMAZÁSA A FELSŐOKTATÁSI INTÉZMÉNYEKNÉL A controlling hasznossága mindaddig nem fog érvényre jutni
Dr. Tóth Antal - Dr. Zéman Zoltán A controlling integrálódása az oktatási szférában 1. CONTROLLING ALKALMAZÁSA A FELSŐOKTATÁSI INTÉZMÉNYEKNÉL A controlling hasznossága mindaddig nem fog érvényre jutni
5. Mérés Transzformátorok
 5. Mérés Transzformátorok A transzformátor a váltakozó áramú villamos energia, feszültség, ill. áram értékeinek megváltoztatására (transzformálására) alkalmas villamos gép... Működési elv A villamos energia
5. Mérés Transzformátorok A transzformátor a váltakozó áramú villamos energia, feszültség, ill. áram értékeinek megváltoztatására (transzformálására) alkalmas villamos gép... Működési elv A villamos energia
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 11 XI LINEÁRIS EGYENLETRENDSZEREk 1 LINEÁRIS EGYENLETRENDSZER A lineáris egyenletrendszer általános alakja: (1) Ugyanez mátrix alakban: (2), ahol x az ismeretleneket tartalmazó
KOVÁCS BÉLA, MATEmATIkA I 11 XI LINEÁRIS EGYENLETRENDSZEREk 1 LINEÁRIS EGYENLETRENDSZER A lineáris egyenletrendszer általános alakja: (1) Ugyanez mátrix alakban: (2), ahol x az ismeretleneket tartalmazó
LIST OF PUBLICATIONS
 Annales Univ. Sci. Budapest., Sect. Comp. 33 (2010) 21-25 LIST OF PUBLICATIONS Péter Simon [1] Verallgemeinerte Walsh-Fourierreihen I., Annales Univ. Sci. Budapest. Sect. Math., 16 (1973), 103-113. [2]
Annales Univ. Sci. Budapest., Sect. Comp. 33 (2010) 21-25 LIST OF PUBLICATIONS Péter Simon [1] Verallgemeinerte Walsh-Fourierreihen I., Annales Univ. Sci. Budapest. Sect. Math., 16 (1973), 103-113. [2]
ESETTANULMÁNY II. A nagyváros és környéke területpolitikai sajátosságai a kistérségi rendszer működése szempontjából. című kutatás
 ESETTANULMÁNY II. A nagyváros és környéke területpolitikai sajátosságai a kistérségi rendszer működése szempontjából című kutatás A program vezetője: Kovács Róbert A kutatás vezetője: Zsugyel János Készítette:
ESETTANULMÁNY II. A nagyváros és környéke területpolitikai sajátosságai a kistérségi rendszer működése szempontjából című kutatás A program vezetője: Kovács Róbert A kutatás vezetője: Zsugyel János Készítette:
Analízisfeladat-gyűjtemény IV.
 Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
AutoCad RAJZFELÜLET BEÁLLÍTÁSAI
 AutoCad RAJZFELÜLET BEÁLLÍTÁSAI Ajánlott klasszikus munkaterület beállítása (menüsor, ikonok egyszerre jelennek meg) Tipp!!! JOBB egérgomb használatával aktuális munkafelületek, menüsorok tulajdonságait
AutoCad RAJZFELÜLET BEÁLLÍTÁSAI Ajánlott klasszikus munkaterület beállítása (menüsor, ikonok egyszerre jelennek meg) Tipp!!! JOBB egérgomb használatával aktuális munkafelületek, menüsorok tulajdonságait
Duna House Barométer. 07. szám. 2011. év 2011. december hónap
 Duna House Barométer 07. szám 2011. év 2011. december hónap Tartalomjegyzék: Éves összefoglaló: ingatlanpiac 2011 Vezetői összefoglaló Tranzakciószám és keresletindex Lakásindexek Lakásindexek - Regionális
Duna House Barométer 07. szám 2011. év 2011. december hónap Tartalomjegyzék: Éves összefoglaló: ingatlanpiac 2011 Vezetői összefoglaló Tranzakciószám és keresletindex Lakásindexek Lakásindexek - Regionális
Gyógytea-fogyasztási szokások napjainkban egy felmérés tapasztalatai
 2015. április GYÓGYSZERÉSZET 207 Gyógyszerészet 59. 207-212. 2015. Gyógytea-fogyasztási szokások napjainkban egy felmérés tapasztalatai Peták Zsolt 1 és Csupor Dezső 2 A gyógyteák csoportja jogi és szakmai
2015. április GYÓGYSZERÉSZET 207 Gyógyszerészet 59. 207-212. 2015. Gyógytea-fogyasztási szokások napjainkban egy felmérés tapasztalatai Peták Zsolt 1 és Csupor Dezső 2 A gyógyteák csoportja jogi és szakmai
Sz-2/14 Belső ellenőrzési Kézikönyv
 3. kiadás 0. módosítás 2 (78). oldal Tartalom I. Bevezetés... 3 II. A belső ellenőrzés hatáskörét, feladatait és céljait meghatározó belső ellenőrzési alapszabály (Charta)... 5 III. A belső ellenőrzési
3. kiadás 0. módosítás 2 (78). oldal Tartalom I. Bevezetés... 3 II. A belső ellenőrzés hatáskörét, feladatait és céljait meghatározó belső ellenőrzési alapszabály (Charta)... 5 III. A belső ellenőrzési
Számítástechnikai és Automatizálási Kutatóintézet (MTA SZTAKI), 1111, Budapest, Kende utca 13 17, email:{vezetéknév.keresztnév}@sztaki.mta.
 Mozgó személyek követése és 4D vizualizációja Lidar-alapú járáselemzéssel Nagy Balázs 1, Benedek Csaba 1 és Jankó Zsolt 2 1 Elosztott Események Elemzése Kutatólaboratórium, Magyar Tudományos Akadémia,
Mozgó személyek követése és 4D vizualizációja Lidar-alapú járáselemzéssel Nagy Balázs 1, Benedek Csaba 1 és Jankó Zsolt 2 1 Elosztott Események Elemzése Kutatólaboratórium, Magyar Tudományos Akadémia,
LOGISZTIKA A TUDOMÁNYBAN ÉS A GAZDASÁGBAN
 Miskolci Egyetem, Multidiszciplináris tudományok, 1. kötet (2011) 1. szám, pp. 11-20. LOGISZTIKA A TUDOMÁNYBAN ÉS A GAZDASÁGBAN Illés Béla tanszékvezető egyetemi tanár Miskolci Egyetem, Anyagmozgatási
Miskolci Egyetem, Multidiszciplináris tudományok, 1. kötet (2011) 1. szám, pp. 11-20. LOGISZTIKA A TUDOMÁNYBAN ÉS A GAZDASÁGBAN Illés Béla tanszékvezető egyetemi tanár Miskolci Egyetem, Anyagmozgatási
Hajdúsági Kistérség Területfejlesztési Koncepciója és Programja HELYZETÉRTÉKELÉS 2005.
 Hajdúsági Kistérség Területfejlesztési Koncepciója és Programja HELYZETÉRTÉKELÉS 2005. Tartalomjegyzék BEVEZETÉS I. A PROGRAMOZÁS MÓDSZERTANI MEGFONTOLÁSAI... 4 II. GAZDASÁG- ÉS IPARFEJLESZTÉS... 14 III.
Hajdúsági Kistérség Területfejlesztési Koncepciója és Programja HELYZETÉRTÉKELÉS 2005. Tartalomjegyzék BEVEZETÉS I. A PROGRAMOZÁS MÓDSZERTANI MEGFONTOLÁSAI... 4 II. GAZDASÁG- ÉS IPARFEJLESZTÉS... 14 III.
2013.03.11. Az SPC alapjai. Az SPC alapjai SPC 5. 5. Az SPC (Statistic Process Control) módszer. Dr. Illés Balázs
 SPC 5 5. Az SPC (Statistic Process Control) módszer Dr. Illés Balázs BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM ELEKTRONIKAI TECHNOLÓGIA TANSZÉK Az SPC alapjai SPC (Statistical Process Controll) =
SPC 5 5. Az SPC (Statistic Process Control) módszer Dr. Illés Balázs BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM ELEKTRONIKAI TECHNOLÓGIA TANSZÉK Az SPC alapjai SPC (Statistical Process Controll) =
MATEMATIKA ÉRETTSÉGI VIZSGA ÁLTALÁNOS KÖVETELMÉNYEI
 A vizsga formája Középszinten: írásbeli. Emelt szinten: írásbeli és szóbeli. MATEMATIKA ÉRETTSÉGI VIZSGA ÁLTALÁNOS KÖVETELMÉNYEI A matematika érettségi vizsga célja A matematika érettségi vizsga célja
A vizsga formája Középszinten: írásbeli. Emelt szinten: írásbeli és szóbeli. MATEMATIKA ÉRETTSÉGI VIZSGA ÁLTALÁNOS KÖVETELMÉNYEI A matematika érettségi vizsga célja A matematika érettségi vizsga célja
A számítógép felhasználása a modern fizika BSc szintű oktatásában
 DOKTORI ÉRTEKEZÉS TÉZISEI A számítógép felhasználása a modern fizika BSc szintű oktatásában Nagy Péter Témavezető: Dr. Tasnádi Péter egyetemi tanár Eötvös Loránd Tudományegyetem Természettudományi Kar
DOKTORI ÉRTEKEZÉS TÉZISEI A számítógép felhasználása a modern fizika BSc szintű oktatásában Nagy Péter Témavezető: Dr. Tasnádi Péter egyetemi tanár Eötvös Loránd Tudományegyetem Természettudományi Kar
Mérnök informatikus (BSc) alapszak levelező tagozat (BIL) / BSc in Engineering Information Technology (Part Time)
 Mérnök informatikus (BSc) alapszak levelező tagozat (BIL) / BSc in Engineering Information Technology (Part Time) (specializáció választás a 4. félévben, specializációra lépés feltétele: az egyik szigorlat
Mérnök informatikus (BSc) alapszak levelező tagozat (BIL) / BSc in Engineering Information Technology (Part Time) (specializáció választás a 4. félévben, specializációra lépés feltétele: az egyik szigorlat
HITELESÍTÉSI ELŐÍRÁS HIDEGVÍZMÉRŐK ÁLTALÁNOS ELŐÍRÁSOK
 HITELESÍTÉSI ELŐÍRÁS HIDEGVÍZMÉRŐK ÁLTALÁNOS ELŐÍRÁSOK HE 6/1-2005 Az adatbázisban lévő elektronikus változat az érvényes! A nyomtatott forma kizárólag tájékoztató anyag! TARTALOMJEGYZÉK 1. AZ ELŐÍRÁS
HITELESÍTÉSI ELŐÍRÁS HIDEGVÍZMÉRŐK ÁLTALÁNOS ELŐÍRÁSOK HE 6/1-2005 Az adatbázisban lévő elektronikus változat az érvényes! A nyomtatott forma kizárólag tájékoztató anyag! TARTALOMJEGYZÉK 1. AZ ELŐÍRÁS
A szabályzat a Pentaquanet Fogyasztói Klub Belépési Nyilatkozat szerves részét képezi. I. Bevezetés
 Pentaquanet Fogyasztói Klub Szervezeti és Működési Szabályzat A szabályzat a Pentaquanet Fogyasztói Klub Belépési Nyilatkozat szerves részét képezi. I. Bevezetés A Pentaquanet klub elsődleges célja egy
Pentaquanet Fogyasztói Klub Szervezeti és Működési Szabályzat A szabályzat a Pentaquanet Fogyasztói Klub Belépési Nyilatkozat szerves részét képezi. I. Bevezetés A Pentaquanet klub elsődleges célja egy
HIDASNÉMETI KÖZSÉG ÖNKORMÁNYZATA POLGÁRMESTERI HIVATALÁNAK SZERVEZETFEJLESZTÉSE. Informatikai tanulmány
 Tel.: 06-1-212-2070,, Fax: HIDASNÉMETI KÖZSÉG ÖNKORMÁNYZATA POLGÁRMESTERI HIVATALÁNAK SZERVEZETFEJLESZTÉSE Informatikai tanulmány Készült az Új Magyarország Fejlesztési terv Államreform Operatív Program
Tel.: 06-1-212-2070,, Fax: HIDASNÉMETI KÖZSÉG ÖNKORMÁNYZATA POLGÁRMESTERI HIVATALÁNAK SZERVEZETFEJLESZTÉSE Informatikai tanulmány Készült az Új Magyarország Fejlesztési terv Államreform Operatív Program
Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK?
 Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK? A BGF KKFK Nemzetközi gazdálkodás és Kereskedelem és marketing szakjain a hallgatók tanrendjében statisztikai és matematikai
Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK? A BGF KKFK Nemzetközi gazdálkodás és Kereskedelem és marketing szakjain a hallgatók tanrendjében statisztikai és matematikai
MPEG-4 alapú átvitel megvalósítása a DVB-T technikában
 MPEG-4 alapú átvitel megvalósítása a DVB-T technikában ENYEDI BALÁZS, KONYHA LAJOS, SZOMBATHY CSABA, TRAN MIN SON, DR.GSCHWINDT ANDRÁS, DR. SZOKOLAY MIHÁLY, DR. FAZEKAS KÁLMÁN Budapesti Mûszaki és Gazdaságtudományi
MPEG-4 alapú átvitel megvalósítása a DVB-T technikában ENYEDI BALÁZS, KONYHA LAJOS, SZOMBATHY CSABA, TRAN MIN SON, DR.GSCHWINDT ANDRÁS, DR. SZOKOLAY MIHÁLY, DR. FAZEKAS KÁLMÁN Budapesti Mûszaki és Gazdaságtudományi
HELYI TANTERV MATEMATIKA tanításához Szakközépiskola 9-12. évfolyam
 HELYI TANTERV MATEMATIKA tanításához Szakközépiskola 9-12. évfolyam Készült az EMMI kerettanterv 51/2012. (XII. 21.) EMMI rendelet alapján. Érvényesség kezdete: 2013.09.01. Utoljára indítható:.. Dunaújváros,
HELYI TANTERV MATEMATIKA tanításához Szakközépiskola 9-12. évfolyam Készült az EMMI kerettanterv 51/2012. (XII. 21.) EMMI rendelet alapján. Érvényesség kezdete: 2013.09.01. Utoljára indítható:.. Dunaújváros,
LÁNG CSABÁNÉ SZÁMELMÉLET. Példák és feladatok. ELTE IK Budapest 2010-10-24 2. javított kiadás
 LÁNG CSABÁNÉ SZÁMELMÉLET Példák és feladatok ELTE IK Budapest 2010-10-24 2. javított kiadás Fels oktatási tankönyv Lektorálták: Kátai Imre Bui Minh Phong Burcsi Péter Farkas Gábor Fülöp Ágnes Germán László
LÁNG CSABÁNÉ SZÁMELMÉLET Példák és feladatok ELTE IK Budapest 2010-10-24 2. javított kiadás Fels oktatási tankönyv Lektorálták: Kátai Imre Bui Minh Phong Burcsi Péter Farkas Gábor Fülöp Ágnes Germán László
Access 2010 Űrlapok és adatelérés
 2 Minden jog fenntartva, beleértve bárminemű sokszorosítás, másolás és közlés jogát is. Kiadja a Mercator Stúdió Felelős kiadó a Mercator Stúdió vezetője Lektor: Gál Veronika Szerkesztő: Pétery István
2 Minden jog fenntartva, beleértve bárminemű sokszorosítás, másolás és közlés jogát is. Kiadja a Mercator Stúdió Felelős kiadó a Mercator Stúdió vezetője Lektor: Gál Veronika Szerkesztő: Pétery István
5. Előadás. Megyesi László: Lineáris algebra, 29. 36. oldal. 5. előadás Lineáris függetlenség
 5. Előadás Megyesi László: Lineáris algebra, 29. 36. oldal. Gondolkodnivalók Vektortér 1. Gondolkodnivaló Alteret alkotnak-e az R n n (valós n n-es mátrixok) vektortérben az alábbi részhalmazok? U 1 =
5. Előadás Megyesi László: Lineáris algebra, 29. 36. oldal. Gondolkodnivalók Vektortér 1. Gondolkodnivaló Alteret alkotnak-e az R n n (valós n n-es mátrixok) vektortérben az alábbi részhalmazok? U 1 =
Produkció mérések. Gyakorlati segédanyag a Mezőgazdasági- és Környezettudományi Kar hallgatóinak
 SZENT ISTVÁN EGYETEM MEZŐGAZDASÁG- ÉS KÖRNYEZETTUDOMÁNYI KAR NÖVÉNYTANI ÉS ÖKOFIZIOLÓGIAI INTÉZET 2103 GÖDÖLLŐ, PÁTER KÁROLY U. 1 TEL:(28) 522 075 FAX:(28) 410 804 Produkció mérések Gyakorlati segédanyag
SZENT ISTVÁN EGYETEM MEZŐGAZDASÁG- ÉS KÖRNYEZETTUDOMÁNYI KAR NÖVÉNYTANI ÉS ÖKOFIZIOLÓGIAI INTÉZET 2103 GÖDÖLLŐ, PÁTER KÁROLY U. 1 TEL:(28) 522 075 FAX:(28) 410 804 Produkció mérések Gyakorlati segédanyag
Minden az adatról. Csima Judit. 2015. február 11. BME, VIK, Csima Judit Minden az adatról 1 / 41
 Minden az adatról Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2015. február 11. Csima Judit Minden az adatról 1 / 41 Adat: alapfogalmak Adathalmaz elvileg bármi, ami információt
Minden az adatról Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2015. február 11. Csima Judit Minden az adatról 1 / 41 Adat: alapfogalmak Adathalmaz elvileg bármi, ami információt
A szakképző iskolát végzettek iránti kereslet és kínálat várható alakulása 2011
 A szakképző iskolát végzettek iránti kereslet és kínálat várható alakulása 2011 Az elemzés a Szakiskolai férőhelyek meghatározása 2011, a regionális fejlesztési és képzési bizottságok (RFKB-k) részére
A szakképző iskolát végzettek iránti kereslet és kínálat várható alakulása 2011 Az elemzés a Szakiskolai férőhelyek meghatározása 2011, a regionális fejlesztési és képzési bizottságok (RFKB-k) részére
INFORMATIKA 1-4. évfolyam
 INFORMATIKA 1-4. évfolyam Célok - A számítógépes munkaszabályainak és a legfontosabb balesetvédelmi előírások megismerése. - A számítógép és perifériáinak kezelési tudnivalóinak megismerése. - Az életkoruknak
INFORMATIKA 1-4. évfolyam Célok - A számítógépes munkaszabályainak és a legfontosabb balesetvédelmi előírások megismerése. - A számítógép és perifériáinak kezelési tudnivalóinak megismerése. - Az életkoruknak
MPEG-4 modell alkalmazása szájmozgás megjelenítésére
 MPEG-4 modell alkalmazása szájmozgás megjelenítésére Takács György, Tihanyi Attila, Bárdi Tamás, Feldhoffer Gergely, Srancsik Bálint Pázmány Péter Katolikus Egyetem Információs Technológia Kar 1083 Budapest
MPEG-4 modell alkalmazása szájmozgás megjelenítésére Takács György, Tihanyi Attila, Bárdi Tamás, Feldhoffer Gergely, Srancsik Bálint Pázmány Péter Katolikus Egyetem Információs Technológia Kar 1083 Budapest
Matematika tanmenet (A) az HHT-Arany János Tehetségfejleszt Program el készít -gazdagító évfolyama számára
 Matematika tanmenet (A) az HHT-Arany János Tehetségfejleszt Program el készít -gazdagító évfolyama számára Ez a tanmenet az OM által jóváhagyott tanterv alapján készült. A tanterv az Országos Közoktatási
Matematika tanmenet (A) az HHT-Arany János Tehetségfejleszt Program el készít -gazdagító évfolyama számára Ez a tanmenet az OM által jóváhagyott tanterv alapján készült. A tanterv az Országos Közoktatási
MECHANIZMUSOK KINEMATIKAI VIZSGÁLATA
 Multidiszciplináris tudományok 3. kötet (2013) 1. sz. pp. 21-26. MECHANIZMUSOK KINEMATIKAI VIZSGÁLATA Nándoriné Tóth Mária egyetemi docens, ME GÉIK Ábrázoló Geometriai tanszék 3515 Miskolc-Egyetemváros,
Multidiszciplináris tudományok 3. kötet (2013) 1. sz. pp. 21-26. MECHANIZMUSOK KINEMATIKAI VIZSGÁLATA Nándoriné Tóth Mária egyetemi docens, ME GÉIK Ábrázoló Geometriai tanszék 3515 Miskolc-Egyetemváros,
oda egy nagy adatbázisba: az eszközök nincsenek egy koncentrált helyre begyűjtve, azaz minden egyes eszközt külön-külön kell megszerezni egy
 Elektronikus hitelesség e-társadalomban mit, miért és hogyan? Erdősi Péter Máté, CISA http://www.erdosipetermate.hu Magyar Elektronikus Aláírás Szövetség, MELASZ elnokseg@melasz.hu Az elektronikus társadalomban
Elektronikus hitelesség e-társadalomban mit, miért és hogyan? Erdősi Péter Máté, CISA http://www.erdosipetermate.hu Magyar Elektronikus Aláírás Szövetség, MELASZ elnokseg@melasz.hu Az elektronikus társadalomban
