EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER ÉS ALKALMAZÁSA SZENZOR LOKALIZÁLÁSI FELADATRA
|
|
|
- Marika Sipos
- 4 évvel ezelőtt
- Látták:
Átírás
1 Alkalmazott Matematikai Lapok 28 (2011), EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER ÉS ALKALMAZÁSA SZENZOR LOKALIZÁLÁSI FELADATRA PÁL LÁSZLÓ ÉS CSENDES TIBOR A cikkben egy intervallum alapú optimalizálási módszer egy új implementációját mutatjuk be. Az algoritmust MATLAB környezetben valósítottuk meg az INTLAB csomagot használva, amely tartalmazza a szükséges intervallum aritmetikai m veleteket és az automatikus dierenciálást is. A numerikus eredmények alapján az új INTLAB alapú implementáció hasonlóan hatékony, mint a C-XSC alapú eredeti algoritmus eltekintve a számítási id t l. A program más hasonló programokkal összevetve könnyen telepíthet és használható. A cikkben vizsgálunk továbbá egy új feltételt a Newton-lépés bekapcsolására, valamint egy szenzorhálózati alkalmazást mutatunk be, és tanulmányozunk az INTLAB alapú algoritmussal. 1. Bevezet A megoldandó feladat az intervallum korlátos globális optimalizálási probléma a következ formában: min x X f(x), ahol f : R n R, X = {x i [x i, x i ], i = 1,..., n}, és x i, x i R, i = 1,..., n. Az f függvényr l általában feltételezzük, hogy sima. A mi algoritmusunk is erre támaszkodik, ennek ellenére nem sima függvények optimalizálására is használható, ha elhagyjuk bel le a Newton-lépést és a konkávitási tesztet. Globális optimalizálási módszerek segítségével nehéz matematikai feladatokat sikerült megoldani az elmúlt id szakban. Ezek a problémák a dinamikus rendszerek [3, 9, 10], a diszkrét geometria, illetve az optimális körpakolás [15, 20] témakörébe tartoznak. Sikeresen alkalmaztuk ezen módszereket továbbá elméleti kémiai feladatokra [2], valamint üzemelhelyezési feladatokban [22]. Célunk egy könnyen használható, megbízható globális optimalizálási módszer implementálása és tesztelése volt MATLAB környezetben. Egy korábbi sikeres implementációnk MATLAB környezetben a GLOBAL [11] nev sztochasztikus globális optimalizálási algoritmus. A jelen cikkben vizsgált eljárás csak egy, a célfüggvény kiszámítására szolgáló szubrutinra támaszkodik. Más információt nem használ a globális optimalizálási
2 18 PÁL LÁSZLÓ ÉS CSENDES TIBOR problémára vonatkozóan. Az eljárás maga határozza meg a célfüggvény gradiensét és Hesse-mátrixát, felhasználva az INTLAB csomag automatikus dierenciáló eljárásait. 2. Az algoritmus és implementálása Az implementált algoritmus egy korlátozás és szétválasztás típusú módszer, amelynek pszeudokódját az 2.1. Algoritmusban adtuk meg. A módszer el dje a Numerical Toolbox for Veried Computing [12] csomagban volt implementálva. Jelenleg a következ gyorsító teszteket tartalmazza: középponti teszt, konkávitási teszt, monotonitási teszt és intervallumos Newton-lépés. A természetes befoglaláson kívül a középponti formulákat is alkalmazzuk mint befoglaló függvényt. Ha a gradiens befoglalása ismert, akkor az el bbi két befoglaló függvény metszete általában jó megközelítést ad a függvény értékkészletére. Az algoritmusban használt jelölések: w(x) = b a, ahol X = [a, b], mid(x) = (a + b)/2, és F az f célfüggvénynek megfelel befoglaló függvény. A keresési tartományok felosztására szeletelést, illetve fejlett felosztási irányt választó [14] szabályokat használunk. A szeletelés azt jelenti, hogy az intervallumot felosztjuk három másik intervallumra a két legmegfelel bb irányt használva. A felosztási irány megválasztása a C típusú szabály ([7, 14]) alapján történik. Az algoritmus egydimenziós feladatok megoldására is alkalmazható. Ebben az esetben a szeletelés helyett egy sima kettéosztást használunk. A felosztás során keletkezett intervallumokat rendezett listában tároljuk valamilyen rendezési szabály alapján. Az algoritmusban a pf heurisztikus paramétert [7] használjuk a lista rendezésére. Pontosabban, mindig a lista legnagyobb pf értékkel rendelkez intervallumát osztjuk fel. Egy el z cikkben [18] a befoglalások legkisebb alsó korlátja szerinti rendezést is vizsgáltunk. Az algoritmus nem keresi meg az összes globális minimum pontot, hanem az els nél leáll, ha az azt tartalmazó intervallum befoglalásának szélessége kisebb, mint Az implementálás során követtük a Markót Mihály Csaba által készített C-XSC alapú program [16] szerkezetét. Természetesen ahol lehetett, használtuk a MATLAB vektor struktúráit. Ez utóbbi programozás technika a processzor cs vezetékének (pipeline) jobb kihasználása révén az eljárás gyorsítását eredményezi. Az algoritmus tartalmaz egy f iterációs struktúrát a 4. sortól a 36. sorig. Az iterációk során két listát kezelünk: egy munka-, valamint egy temporális listát. Minden iteráció elején meghatározzuk az optimális vágási irányokat (5. sor), majd ezek alapján felosztjuk az aktuális intervallumot három másik intervallumra (6. sor). A 8. és 15. sorok között rendre a kapott intervallumokra végrehajtunk egy monotonitási- (8. sor), egy kivágási tesztet (10. sor), valamint alkalmazzuk a
3 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER 19 Algorithm 2.1 A tanulmányozott intervallum korlátos globális optimalizálási algoritmus 1. function GlobalOptimize (f, X, ϵ) 2. L work := ; L temp := 3. Y := X; f := F (mid(x)) 4. repeat 5. OptimalComponents(Y, k 1, k 2 ) 6. Trisection(Y, k 1, k 2, U 1, U 2, U 3 ) 7. for i := 1 to 3 do 8. if MonotonicityTest( F (U i )) then next i 9. f U := F (U i ) 10. if f < f U then next i 11. f U := f U CenteredForm(U i, F (U i )) 12. if F (mid(u i )) < f then 13. f := F (mid(u i )) 14. L work := CutOffTest(L work, f) 15. if f f U then L temp := L temp (U i, f U ) 16. if length(l temp ) = 1 then 17. U := Head(L temp ) 18. if not ConcavityTest( 2 F (U)) then 19. NewtonStep(f, U, 2 F (U), V, p) 20. for i := 1 to p do 21. if MonotonicityTest( F (V i )) then next i 22. f V := F (V i ) CenteredForm(V i, F (V i )) 23. if F (mid(v i )) < f then 24. f := F (mid(v i )) 25. L work := CutOffTest(L work, f) 26. if f f V then L work := L work (V i, f V ) 27. else 28. while L temp do 29. U := Head(L temp ) 30. L work := L work (U, f U ) 31. if L work then 32. Y := Head(L work ) 33. if w(f Y ) < ϵ then 34. f := [f Y, f] 35. return Y, f 36. until L work =
4 20 PÁL LÁSZLÓ ÉS CSENDES TIBOR középponti formulát (11. sor). A 14. sorban a munka listát aktualizáljuk az új fels korlát alapján. Ha az aktuális intervallumot nem sikerült eldobni az el bbi lépések során, akkor tároljuk a temporális listában (15. sor). A három intervallum feldolgozása után, ha a temporális lista csak egy elemet tartalmaz (16. sor), akkor erre végrehajtunk egy konkávitási tesztet (18. sor) valamint egy Newtonlépést (19. sor). A Newton-lépés eredményeként kapott intervallumokra a korábban leírt lépéseket hajtjuk végre. Ha a lista több mint egy elemet tartalmaz, akkor ezeket tároljuk a munka listában (30. sor). Az iteráció végén (31. és 35. sorok között), ha a munka lista nem üres, akkor kivesszük annak els elemét, és megvizsgáljuk, hogy az intervallum befoglalásának szélessége kisebb-e, mint egy el re megadott érték (33. sor). Ha ez a feltétel teljesül, akkor az intervallumot és az optimum értéket tartalmazó intervallummal együtt visszaadjuk eredményként (35. sor), különben folytatjuk a következ iterációval. Az új algoritmus használatához szükség van az INTLAB csomag [19] telepítésére. Az INTLAB csomagot a Hamburgi Egyetemen fejlesztette ki Siegfried M. Rump és ingyenesen használható nem kereskedelmi céllal, illetve a kutatásban is. A program számos MATLAB verzió alatt volt tesztelve egészen az R2009b változatig. A csomag a helyr l tölthet le, ahol található egy telepítési útmutató is. Letöltés után a programot ki kell csomagolni, majd MATLAB környezetben futtatni kell a startintlab.m szkriptet, amely tulajdonképpen telepíti a csomagot. Az INTLAB 5.5 és korábbi verziói esetén el fordulhat, hogy nem sikerül a telepítés. Ennek az lehet az oka, hogy a MATLAB az Intel Math Kernel Library (IMKL) csomagot használja a numerikus m veletekre. A megoldás az, hogy az Atlas könyvtárat használjuk az IMKL helyett. A Windows rendszer alatt a BLAS_VERSION környezeti változót kell beállítani az atlas***.dll értékre, ahol a '***' a processzor típusát jelenti (Pentium 4 esetén 'atlas_p4.dll'). A szükséges fájl a...\matlab\bin\win32\ mappában található. Az új 6.0 verzió esetén a környezeti változó beállítása nélkül is problémamentesen települ az INTLAB. Linux alatt a következ utasítással állíthatjuk be a megfelel könyvtárat: export BLAS_VERSION="atlas_P4.so" Lényeges, hogy telepítés után valahányszor szükség van az INTLAB csomagra, mindig el kell indítani azt a startintlab paranccsal. Az INTLAB elindítása után új intervallumot az alábbi utasítás segítségével hozhatunk létre: infsup(a,b). Az intervallumok alapértelmezett megjelenítési formája a bizonytalanságot megjelenít mód. Például
5 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER 21 eredménye a = infsup(3.14, 3.15) intval a = 3.15_. A hagyományos intervallum megjelenítési formát az intvalinit('displayinfsup') paranccsal állíthatjuk be, amelynek eredményeképpen az intervallum kiírási alakja: intval a = [3.14, 3.15]. Intervallumokkal persze különböz m veleteket is végezhetünk. Például az x=infsup(0,1); és y=infsup(2,3); intervallumok osztásának eredménye (x/y): Míg sin(x) az intval ans = [0.0000, ]. intval ans = [0.0000, ] intervallumot eredményezi. Számos más példát és bemutató programot találhatunk az INTLAB [19] leírásában. Az új MATLAB/INTLAB alapú intervallumos globális optimalizálási program letölthet a csendes/reg/regform.php címr l. A letöltött csomag tartalmazza a szükséges állományokat és a tesztkörnyezetet is. 3. Az intervallumos globális optimalizáló program használata Az intervallumos globális optimalizáló programot viszonylag egyszer használni, ugyanis a felhasználónak csak az optimalizálandó feladatot kell elhelyeznie a TestFunctions mappába, majd futtatni a MainTester programot. A mappába egyszerre több feladatot is be lehet tenni, és megoldani. Az optimalizálandó problémát két állomány segítségével kell megadni. Az egyik (ennek neve *.bnd lesz) tartalmazza a feladat olyan adatait, mint például a feladat neve, dimenziója, intervallum korlátok a változókra, és a megkövetelt pontosság. A másik fájl pedig a célfüggvényt adja meg (a neve *.m). Például a Shekel-5 standard globális optimalizálási tesztfeladat esetén a két állomány sh5.bnd és sh5.m. Az sh5.bnd fájl tartalma:
6 22 PÁL LÁSZLÓ ÉS CSENDES TIBOR S e-8 A célfüggvényt tartalmazó sh5.m állomány tartalma pedig: function y = sh5(x) m = 5; a = ones(10,4); a(1,:) = 4.0*a(1,:); a(2,:) = 1.0*a(2,:); a(3,:) = 8.0*a(3,:); a(4,:) = 6.0*a(4,:); for j = 1:2; a(5,2*j-1) = 3.0; a(5,2*j) = 7.0; a(6,2*j-1) = 2.0; a(6,2*j) = 9.0; a(7,j) = 5.0; a(7,j+2) = 3.0; a(8,2*j-1) = 8.0; a(8,2*j) = 1.0; a(9,2*j-1) = 6.0; a(9,2*j) = 2.0; a(10,2*j-1)= 7.0; a(10,2*j)= 3.6; end c(1) = 0.1; c(2) = 0.2; c(3) = 0.2; c(4) = 0.4; c(5) = 0.4; c(6) = 0.6; c(7) = 0.3; c(8) = 0.7; c(9) = 0.5; c(10)= 0.5; s = 0.0; for j = 1:m; p = 0.0; for i = 1:4 p = p+(x(i)-a(j,i))^2; end s = s+1.0/(p+c(j)); end y = -s; A MainTester futtatása után az eredményt az alábbi formában kapjuk meg: Function name: S5 The set of global minimizers is located in the union of the following boxes: c1: [ , ]
7 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER 23 [ , ] [ , ] [ , ] The global minimum is enclosed in: [ , ] Statistics: Iter Feval Geval Heval MLL CPUt(sec) El fordulhat természetesen, hogy eredményként több intervallumot is kapunk. A globális minimum pontok ezen intervallumok egyesítésében találhatók. Az eredmény kiírt alakja tartalmazza a feladat megoldása során mért szokásos hatékonysági mutatókat: az iteráció számot, a függvényhívások számát, a gradienshívások számát, a Hesse-mátrix kiértékelések számát, a maximális lista hosszat és a CPU id t. Az optimalizáló eljárás közvetlenül, parancssorból is használható a következ módon: >> addpath('./','./utils','testfunctions') >> amin = [0; 0; 0; 0] >> amax = [10; 10; 10; 10] >> b = infsup(amin,amax) >> [intv, min, stats] = GOP(@sh5, b, 1e-8) Lehet ség van arra is, hogy úgy használjuk az opimalizáló eljárást, hogy a szükséges két állományt nem adjuk meg, hanem a célfüggvényt inline módon deniáljuk. Erre tekintsük az alábbi példát: >> f = inline('x(1)^2+x(2)^2+1') >> amin = [-2; -2] >> amax = [1; 1] >> int = infsup(amin,amax) >> [intv, min, stat] = GOP(f, int, 1e-8) 4. A C-XSC alapú algoritmus és az INTLAB alapú módszer összehasonlítása Az INTLAB alapú algoritmust numerikusan teszteltük. A célunk az volt, hogy megvizsgáljuk ennek hatékonyságát a szokásos hatékonysági mutatókkal, valamint
8 24 PÁL LÁSZLÓ ÉS CSENDES TIBOR összehasonlítani a kapott eredményeket a C-XSC alapú algoritmus megfelel mutatóival. A teszteket MATLAB R2008a környezetben, INTLAB 5.5-ös verzió alatt végeztük, Pentium 4-es (2 Gbyte RAM memóriával ellátott, Core 2 Duo, 2 GHz-es processzorú) számítógépen. A tesztfeladatok halmaza tartalmazta az összes standard globális optimalizálási függvényt is. Hasonló feladathalmazon végeztünk tesztelést a [7, 8] cikkekben. A numerikus eredményeket az 1. és 2. táblázatokban összegeztük. A táblázatok els két oszlopa a probléma nevét és dimenzióját tartalmazza. A függvény nevek helyett azok rövidítéseit használtuk, például Shekel-5 helyett S5, Schwefel 3.2 helyett Sch3.2, Ratz-4 helyett R4 szerepel stb. A többi oszlop a szokásos hatékonysági mutatókat tartalmazza, mint amilyen az iteráció szám (ITSz), a függvényhívások száma (FHSz), a gradienshívások száma (GHSz), a Hesse-mátrix kiértékelések száma (HHSz), a maximális munka lista hossza (MLH) és a szükséges CPU id másodpercben (CPU). A két implementáció esetén a hatékonysági mutatók (egy, a CPU id kivételével) megegyeznek, vagy hasonlók. Ez nagyjából annak tudható be, hogy a két algoritmus struktúrája közel megegyezik. A CPU id esetén nagy eltérés gyelhet meg. Az INTLAB alapú implementáció átlagosan 442-szer több id t igényel ugyanannak a feladatnak a megoldásához. Az arányok az egyes feladatok esetén 16 és 1251 között változnak, és a médián értéke erre az arányra 345. A nagyobb számok azon feladatok esetén gyelhet k meg, ahol sok számításra volt szükség. A nagy futásid beli különbségek a MATLAB interpreter módban való m ködésének tudhatók be. Az összehasonlítás eredményeképpen elmondható, hogy MATLAB környezetben az INTLAB alapú algoritmus egyszer en használható, viszont hátránya a sebesség visszaesése. Ennek ellenére az új globális optimalizálási módszer hasznos modellez eszköz lehet optimalizálási feladatok kezdeti tanulmányozására. Különösen igaz ez olyan feladatok esetén, amelyekre a CPU id a növekedés ellenére is elfogadható mérték (legföljebb pár perc). A számítási környezet interaktivitása el nyös olyan esetekben, amikor kezdeti lehet ségek közötti választás céljából nagy számú kísérletet végzünk eltér beállításokkal, illetve modellekkel. 5. A Newton-lépés bekapcsolásának vizsgálata A Newton-lépést az algoritmus gyorsítására használjuk. Tulajdonképpen egy intervallumos NewtonSeidel-lépést alkalmazunk a célfüggvény gradiensére, ezáltal megpróbálunk közeli korlátokat adni a minimum helyekre. A teljes Newtonalgoritmust nem futtatjuk le, mert az túl költséges lenne, ezért alkalmazunk csak iterációnként egy-egy lépést.
9 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER táblázat. A C-XSC- és az INTLAB alapú algoritmusok eredményeinek összehasonlítása. A táblázatban Dim a feladat dimenzióját jelenti, ITSz az iteráció számot, FHSz a függvényhívások számát, és GHSz a gradiens hívások számát. A C-XSC kód Az INTLAB kód Feladat Dim ITSz FHSz GHSz ITSz FHSz GHSz S S S H H GP SHCB THCB BR RB RB L L L L L L L L L L L L Schw Schw Schw Schw Schw Schw Schw3.7_ Schw3.7_ Griew Griew R R R R R EX
10 26 PÁL LÁSZLÓ ÉS CSENDES TIBOR 2. táblázat. A C-XSC -és az INTLAB alapú algoritmusok eredményeinek összehasonlítása. A táblázatban Dim a feladat dimenzióját jelenti, HHSz a Hesse-mátrix kiértékelések számát, MLH a maximális lista hosszát, valamint CPU a futási id t másodpercben. A C-XSC kód Az INTLAB kód Feladat Dim HHSz MLH CPU HHSz MLH CPU S S S H H GP SHCB THCB BR RB RB L L L L L L L L L L L L Schw Schw Schw Schw Schw Schw Schw3.7_ Schw3.7_ Griew Griew R R R R R EX
11 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER 27 A Newton-lépés alkalmazása minden egyes részintervallumra szintén költséges lenne, ezért célszer valamilyen feltételt használni ennek bekapcsolására. Egy korábbi cikk [16] alapján algoritmusunkban a Newton-lépést csak abban az esetben használtuk, ha a felosztás során keletkezett három részintervallumból a többi gyorsító lépés végrehajtása után már csak egy részintervallum maradt. A továbbiakban egy új bekapcsolási feltételt vizsgálunk. Ennek az a lényege, hogy minden olyan részintervallumra alkalmazzuk a Newton-lépést, amelynek szélessége kisebb, mint egy el re megadott érték, ugyanis a Newton-lépés igazából akkor hatékony, ha az adott argumentum intervallum már elég kicsi. Az új feltételben 0.1 értéket használtunk az intervallum szélessége küszöbértékének Elméleti vizsgálat Vannak esetek, amikor az el bbi feltételt alkalmazva a Newton-lépés nem eredményes abban az értelemben, hogy vagy nem is csökken az intervallum mérete, vagy sok darabra osztja fel az aktuális intervallumot. A gyakorlatban többnyire az utóbbi eset szokott el fordulni, amely azért nem el nyös, mert hasonló eredményt érhetünk el egyszer kettéosztással is, de jóval kisebb költséggel. A Newton-lépés hatékonysága több-dimenziós esetben méginkább romolhat, ugyanis a dimenzió növekedéssel az új részintervallumok száma is növekszik. A továbbiakban feltételezzük, hogy a másodrend derivált befoglalása, amelyre a Newton-lépés nem eredményes, az alábbi alakú: F uj(x) = [ F (X) D w(f (X)), F (X) + D w(f (X)) ], (1) ahol F (X) a másodrend derivált egy befoglalása az X intervallumon, és D egy pozitív valós szám. F (X) lehet a másodrend derivált értékkészlete is X-en. Hasonló alakú befoglalófüggvényt feltételeztek az [5, 6] cikkekben is, a gyakorlatban használt befoglaló függvények körében a szimmetrikus túlbecslés gyakori. A következ két tétel arra akar rávilágítani, hogy milyen esetekben nem lesz a Newton-lépés hatékony Tétel. Adott f egyváltozós függvény és X, w(x) < ϵ intervallum esetén létezik olyan befoglaló függvény, amelyre a Newton-lépés nem eredményes abban az értelemben, hogy vagy nem is csökken az intervallum mérete, vagy sok darabra osztja fel az X intervallumot. Bizonyítás. Az egydimenziós f(x) függvény esetén a Newton-iteráció az alábbi összefüggésekkel írható le: ( N X (k), x (k)) = x (k) f ( x (k)) F ( X (k)), (2) ( X (k+1) = X (k) N X (k), x (k)), k = 1, 2,... (3)
12 28 PÁL LÁSZLÓ ÉS CSENDES TIBOR ahol x (k) = mid(x (k) ), f az els rend derivált, F a másodrend derivált befoglalása. Legyen egy, a w(x) < ϵ feltételnek megfelel X = [a, b] intervallum és F (X) = [c, d]. A Newton-lépés akkor nem eredményes, ha a (2) egyenletben a másodrend derivált tartalmazza a nullát, és a metszetképzés (3) után eredményként két intervallumot kapunk. A Newton-lépés ezen eredménye azért nem hasznos, mert ezt elérhetjük egy egyszer kettéosztással is, amely olcsóbb m velet, mint a Newton-lépés. A kérdés az, hogy milyen túlbecslésre van szükség ahhoz, hogy a másodrend derivált befoglalása tartalmazza a nullát és a metszetképzés után két intervallumot kapjunk eredményül. A továbbiakban feltételezzük, hogy 0 / F (X) és F uj (X) = [c, d ]. A feladat c és d értékeit úgy meghatározni, hogy 0 F uj (X) teljesüljön. A korábbi jelölésekkel a Newton-operátor a következ alakú lesz: N(X, x) = x f ( x) F uj ( x) [c, d ]. (4) ( [ ) ] 1. Eset: amikor f ( x) > 0. Ekkor N(X, x) =, x f ( x) d x f ( x) c,. Az X N(X, x) m velet eredményeként akkor kapunk két intervallumot, ha teljesül a < x f ( x) d, (5) b > x f ( x) c. (6) Az (5) és (6) egyenl tlenségekb l rendre azt kapjuk, hogy: d > 2 f ( x) w(x), (7) c < 2 f ( x) w(x). (8) A (7) és (8), valamint az (1) összefüggésekb l következik: c D w(f (X)) < 2 f ( x) w(x), (9) d + D w(f (X)) > 2 f ( x) w(x). (10) Innen D-re a következ egyenl tlenségek adódnak: D > D 1 = 2 f ( x) + c w(x) w(x) w(f (X)), (11)
13 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER 29 D > D 2 = 2 f ( x) d w(x) w(x) w(f (X)). (12) Tehát, ha D > max(d 1, D 2 ), akkor a Newton-lépés eredményeként két intervallumot kapunk. ( ] [ ) 2. Eset: amikor f ( x) < 0. Ekkor N(X, x) =, x f ( x) c x f ( x) d,. Az els esethez hasonló gondolatmenettel azt kapjuk D-re, hogy: D > D 1 = 2 f ( x) + c w(x) w(x) w(f, (13) (X)) D > D 2 = 2 f ( x) d w(x) w(x) w(f. (14) (X)) Tehát ebben az esetben, ha D > max(d 1, D 2 ), akkor a Newton-lépés nem lesz eredményes. Az el bbi bizonyításban a D 1 és D 2 értékek segítségével olyan befoglalását kapjuk a másodrend deriváltnak, amelyre a Newton-módszer két intervallumot ad eredményül. Mivel szimmetrikus túlbecslést feltételeztünk a másodrend derivált befoglalására, ezért D értékéül a D 1 és D 2 közül nyilván a nagyobbikat választjuk. Az 1. esetnek megfelel en, ha most azt vizsgáljuk, hogy a Newton-lépés mikor hatékony, akkor a következ összefüggést kapjuk: D D 1 = 2 f ( x) + c w(x) w(x) w(f (X)). (15) Ezen összefüggés alapján ismert D túlbecslési paraméter mellett megadható olyan ϵ küszöbérték a Newton-lépés bekapcsolására, amely biztosítani tudja, hogy a Newton-lépés hatékony legyen abban az értelemben, hogy eredményül egy sz kebb intervallumot kapjunk, mint az argumentum intervallum. Az (15) összefüggés alapján 2 f ( x) w(x) D w(f (X)) c. Tehát, ha ϵ = 2 f ( x) D w(f (X)) c, akkor a Newton-lépés eredményeként sz kebb intervallumot kapunk, mint az argumentum intervallum. Hasonló állítás vezethet le arra az esetre is, ha f ( x) < 0 (ez a 2. eset az 1. tétel bizonyításában).
14 30 PÁL LÁSZLÓ ÉS CSENDES TIBOR Egy F (X) befoglaló függvényt akkor mondunk izotonnak, ha X Y -ból F (X) F (Y ) következik. Ez a tulajdonsága csaknem minden, a számítógépes eljárásokban használatos befoglalófüggvénynek megvan. Az (1)-ben deniált F uj függvény nyilvánvalóan minden rögzített D értékre izoton függvény. A következ állítás mégis azt mondja ki, hogy amennyiben a D konstans értékét úgy kell megválasztani, hogy a Newton-lépés ne legyen eredményes, akkor az így adódó befoglaló függvény nem lesz izoton Állítás. Az 1. tétel bizonyításában megkonstruált F uj befoglalófüggvény nem izoton. Bizonyítás. Ennek belátására elegend ellenpéldát mutatni. Az f(x) = 1 20 (x + 4)(x + 2)(x + 1)(x 1)(x 3) + 2 függvény esetén az (1) összefüggéssel és az 1. tétel bizonyításában kidolgozott konstrukcióval megadott befoglaló függvény nem izoton az alábbi intervallumokra. Ha X 1 = [ 1.60, 1.5], akkor D > Ha D = 3.76, akkor F uj (X 1) = [ 1.41, 7.46]. Ha X 2 = [ 1.65, 1.45], akkor D > Ha D = 1.31, akkor F uj (X 2) = [ 0.70, 6.81]. Ha X 3 = [ 1.7, 1.4], akkor D > Ha D = 0.64, akkor F uj (X 3) = [ 0.46, 6.67]. A példa esetén tehát X 1 X 2 X 3 és F uj (X 3) F uj (X 2) F uj (X 1), azaz az el írt tulajdonsággal rendelkez F uj nem izoton. Az 5.1. állítás lényegi jelentése tehát az, hogy elegend en kicsi ϵ döntési paraméter választása esetén a Newton-lépés eredményességének esélye növelhet Tétel. Adott f többváltozós függvény és X, w(x) < ϵ intervallum esetén létezik olyan befoglaló függvény, amelyre a Newton-lépés nem lesz hatékony, abban az értelemben, hogy vagy nem is csökken az intervallum mérete, vagy sok darabra osztja fel az X intervallumot. Bizonyítás. Többváltozós esetben a Newton-módszer iterációs sémája a következ formában írható: ( G x (k)) ( + H X (k)) ( ( N X (k), x (k)) x (k)) = 0 (16) X (k+1) = X (k) N ( X (k), x (k)), k = 1, 2,..., (17) ahol x (k) = mid ( X (k)), G a gradiens, és H a Hesse mátrix befoglalása. Az N érték meghatározására a HansenSengupta-operátort használjuk. Ez az operátor a GaussSeidel-eljárást alkalmazza. A (16) egyenletet H(X) középponti inverzével, C-vel prekondicionálva kapjuk, hogy C H(X)(N(X, x) x) = C G( x).
15 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER 31 Bevezetve az M = C H(X), b = C G( x) mennyiségeket, a komponensenkénti intervallumos GaussSeidel-eljárás ( N X (k), x (k)) b i + ( ) i 1 = x (k) j=1 M ij X (k+1) j x (k+1) j i + M ii ) n j=i+1 M ij (X (k) j x (k) j +, M ii X (k+1) i = X (k) i N (18) ( X (k), x (k)) (19) alakú lesz, ahol x (k) = mid ( X (k)) és k = 1, 2,.... Az iterációban, ha az N ( X (k), x (k)) i-dik komponensét kiszámoltuk, akkor elvégezzük a metszetképzést. A (18) összefüggésb l látszik, hogy minden iterációs lépésben az M mátrix egy f átlóbeli elemével osztunk. Az egyváltozós esett l eltér en, itt nem a másodrend derivált befoglalását használjuk, hanem a Hesse-mátrix egy prekondicionált változatát. A prekondicionálás célja, hogy az M H(X) szorzás eredményeképpen olyan mátrixot kapjunk, amelynek együtthatói jobban kezelhet k a rendszer megoldása során, mint az eredeti mátrix esetén. A (18) egyenlet hasonló a (2) egyenlethez, így a bizonyítás is hasonlóan történik, mint az egyváltozós esetben. A különbség itt az, hogy úgy kell meghatározni a befoglalást, hogy a Hesse-mátrix középponti inverzével való szorzás után tartalmazza a nullát, és a metszetképzés során két intervallumot kapjunk. Az adott iteráció i. bels lépésében, ha 0 M ii, i = 1,..., n és a Newton-lépés eredményeként az i. komponens két intervallum egyesítéseként írható fel, akkor a Newton-lépés két külön részfeladatra osztható. Ezekben a részfeladatokban a kapott i. komponenst helyettesítjük az egyesítésben szerepl egyik intervallummal. Tehát, ha egy komponens esetén igaz a fenti állítás, akkor a Newton-lépés már nem lesz eredményes Numerikus vizsgálat Az INTLAB alapú algoritmust teszteltük az új feltétellel és a kapott eredményeket összehasonlítottuk az eredeti feltétellel elért eredményekkel. A tesztkörnyezet beállításai megegyeznek a korábban leírt beállításokkal. A 3. és 4. táblázatok tartalmazzák a függvényekre az eredményeket, valamint az egyes mutatók összesített és átlag értékeit a teljes célfüggvény halmazra vonatkozóan. A két feltételt a kapott hatékonysági mutatókkal nehéz összehasonlítani, ugyanis ezek értékei lényegesen, és persze érthet módon különböznek az új feltételnek köszönhet en. Ezért célszer bb a két feltételnek megfelel CPU id ket összehasonlítani a teljes függvényhalmazra. A teljes futásid t tekintve megállapítható, hogy az új feltétel esetén ez 14 perccel (15%-al) kevesebb, mint a régi esetén. Figyelembe véve azt, hogy az EX2 és a
16 32 PÁL LÁSZLÓ ÉS CSENDES TIBOR Schw függvények együttesen a teljes futásid 80 százalékát igénylik, érdemes megvizsgálni az eredményeket e két feladat elhagyásával. Ebben az esetben azt találjuk, hogy az új feltétel esetén a teljes futásid 6 perccel (30%-al) lett kevesebb, mint a régi feltétellel. Az eredmények alapján elmondható, hogy az új feltétel segítségével sikerült a szükséges számítási id t lényegesen csökkenteni. Ez a javulás mégis nem minden függvényen gyelhet meg, s t egyes estekben (pl. Schw3.7.10) rosszabb értéket kaptunk. Ez azt jelenti, hogy nehéz az új feltétel számára olyan értéket beállítani, amely minden vizsgált feladatra javulást eredményez. A jöv ben ennek az értéknek az adaptív beállítását fogjuk megvizsgálni. A teljes elméleti gondolatmenet hasonló formában megismételhet olyan befoglaló függvényekre is, amelyek túlbecslése nem szimmetrikus Numerikus vizsgálat Az INTLAB alapú algoritmust teszteltük az új feltétellel és a kapott eredményeket összehasonlítottuk az eredeti feltétellel elért eredményekkel. A tesztkörnyezet beállításai megegyeznek a korábban leírt beállításokkal. A 3. és 4. táblázatok tartalmazzák a függvényekre az eredményeket, valamint az egyes mutatók összesített és átlag értékeit a teljes célfüggvény halmazra vonatkozóan. A két feltételt a kapott hatékonysági mutatókkal nehéz összehasonlítani, ugyanis ezek értékei lényegesen, és persze érthet módon különböznek az új feltételnek köszönhet en. Ezért célszer bb a két feltételnek megfelel CPU id ket összehasonlítani a teljes függvényhalmazra. A teljes futásid t tekintve megállapítható, hogy az új feltétel esetén ez 14 perccel (15%-al) kevesebb, mint a régi esetén. Figyelembe véve azt, hogy az EX2 és a Schw függvények együttesen a teljes futásid 80 százalékát igénylik, érdemes megvizsgálni az eredményeket e két feladat elhagyásával. Ebben az esetben azt találjuk, hogy az új feltétel esetén a teljes futásid 6 perccel (30%-al) lett kevesebb, mint a régi feltétellel. Az eredmények alapján elmondható, hogy az új feltétel segítségével sikerült a szükséges számítási id t lényegesen csökkenteni. Ez a javulás mégis nem minden függvényen gyelhet meg, s t egyes estekben (pl. Schw3.7.10) rosszabb értéket kaptunk. Ez azt jelenti, hogy nehéz az új feltétel számára olyan értéket beállítani, amely minden vizsgált feladatra javulást eredményez. A jöv ben ennek az értéknek az adaptív beállítását fogjuk megvizsgálni. 6. Alkalmazás 6.1. Lokalizálás szenzorhálózatokban Szenzorhálózati alkalmazásokban nagyon gyakran szükség van az egyes csomópontok földrajzi pozícióinak az ismeretére. Ezért az egyik legfontosabb elvárás az ilyen hálózatokban a csomópontok helymeghatározó képessége. Az elmúlt id szakban számos módszert [1, 4, 13, 17] dolgoztak ki szenzorok lokalizálására.
17 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER táblázat. A Newton-lépés bekapcsolásának vizsgálata az INTLAB alapú algoritmus esetén. A táblázatban Dim a feladat dimenzióját jelenti, ITSz az iteráció számot, FHSz a függvényhívások számát, GHSz pedig a gradiens hívások számát. Eredeti feltétel Új feltétel Feladat Dim ITSz FHSz GHSz ITSz FHSz GHSz S S S H H GP SHCB THCB BR RB RB L L L L L L L L L L L L Schw Schw Schw Schw Schw Schw Schw3.7_ Schw3.7_ Griew Griew R R R R R EX Összeg Átlag
18 34 PÁL LÁSZLÓ ÉS CSENDES TIBOR 4. táblázat. A Newton-lépés bekapcsolásának vizsgálata az INTLAB alapú algoritmus esetén. A táblázatban Dim a feladat dimenzióját jelenti, HHSz a Hesse mátrix kiértékelések számát, MLH a maximális lista hosszát, valamint CPU a futási id t másodpercben. Eredeti feltétel Új feltétel Feladat Dim HHSz MLH CPU HHSz MLH CPU S S S H H GP SHCB THCB BR RB RB L L L L L L L L L L L L Schw Schw Schw Schw Schw Schw Schw3.7_ Schw3.7_ Griew Griew R R R R R EX Összeg Átlag
19 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER 35 Az általános szenzor lokalizálási feladat a következ képpen fogalmazható meg. Adott m darab szenzor csomópont ismert pozíciókkal: a k R l, k = 1,..., m, valamint n darab csomópont, ismeretlen pozíciókkal x j R l, j = 1,..., n. Két tetsz leges csomópont esetén bevezetjük a következ euklideszi távolságokat: d kj = a k x j, egy ismert és egy ismeretlen pozíciójú csomópont esetén, valamint d ij = x i x j, két ismeretlen pozíciójú csomópont esetén, ahol j = 1,..., n és i j. Távolságalapú alkalmazásoknál a csomópontok jeleket bocsátanak ki, amelyek segítségével a szomszédos csomópontok képesek az egymás közötti távolságokat becsülni. Egy csomópont szomszédai azon csomópontok, amelyek az adott csomópont hatókörén bel l vannak. Az összes rögzített és nem rögzített csomópontokra értelmezzük a következ halmazokat: N k = {(k, j) : d kj r k }, j = 1,..., n, N i = {(i, j) : d ij r i }, j = 1,..., n, ahol az r k és r i paraméterek a maximális hatókörök sugarai. A d kj és d ij valós távolságok helyett általában a csomópontok által mért d kj, d ij zajos távolságokat szokták használni. Az utóbbiak a valós távolságoknak egy zajjal módosított változatai. Tehát a lokalizálási feladat: adottak a d kj, d ij zajos távolságok, és az ismert csomópontok koordinátái a k R l, k = 1,..., m felhasználásával határozzuk meg a többi csomópont x j R l, j = 1,..., n pozícióit. A feladat megfogalmazható szemidenit programozásként [4], vagy nemlineáris optimalizálási feladatként [13]. Mi az utóbbi lehet séget választottuk, amelyben a cél egy nemlineáris hibafüggvény minimalizálása: min x m ( a k x j d ) 2 n kj + ( x i x j d ) 2 ij, (20) k=1 j N k i=1 j N i ahol x i, x j az i és j csomópontok becsült pozíciói, dkj és d ij a mért távolságok a (k, j) és (i, j) csomópont párok között és N i, N k a szomszédos csomópont halmazok A feladat megoldása A korábban megfogalmazott lokalizálási problémát számos sztochasztikus módszerrel sikerült közelít leg megoldani. A leggyakrabban használt módszer a szimulált h tés [1, 13, 17] és a genetikus algoritmus [23]. A (20) célfüggvénnyel megadott feladat egy globális optimalizálási feladat, amelyet mi intervallum aritmetikán alapuló módszerrel próbáltunk megoldani. A feladatban minden ismeretlen pozíciójú csomópont mindkét koordinátájához egy intervallum változót rendeltünk. A csomópontok a sík [0, 1] [0, 1] tartományában helyezkednek el, így az intervallum változók is ezen a tartományon belül változnak.
20 36 PÁL LÁSZLÓ ÉS CSENDES TIBOR A (20) célfüggvény minimumának a megkeresése az INTLAB alapú optimalizálóval nagyon id igényes m velet, ezért egy közelít megoldás megtalálására az ívmetszés [17, 21] technikáját alkalmazzuk használva az INTLAB alapú programot. Az ívmetszés lényege, hogy ha egy ismeretlen pozíciójú csomópontnak van három ismert helyzet szomszédja, akkor az el bbi helyzete egyértelm en meghatározható, amennyiben ismertek a csomópontok közötti valós távolságok. Mivel a távolságok zajosak, ezért általában nem létezik egyértelm megoldás, így azt a pontot keressük meg, amely minimalizálja az ismert helyzet csomópontoktól vett távolságok összegét. A feladat megoldása során a csomópontokat két halmazba csoportosítjuk: az ismert és az ismeretlen helyzet csomópontok halmazába. Minden ismeretlen helyzet csomópont esetén meghatározzuk a szomszédait, majd az ívmetszés segítségével kiszámoljuk a pozícióját. A meghatározott helyzet csomópontot áthelyezzük az ismert pozíciójú csomópontok halmazába és felhasználjuk más ismeretlen helyzet csomópont helyzetének meghatározására. A mi esetünkben, ahol lehetséges, ott négy szomszédos csomópontot választunk a pontosabb meghatározás érdekében. A lokalizálási feladat megoldása nagymértékben függ a különböz csomópontok számától, a rögzített szenzorok pozíciójától, a szomszédos csomópontok számától, a mért távolságok hibájától és a hatókörsugarától. Az általunk vizsgált feladatokban 5 ismert, valamint 50 ismeretlen pozíciójú csomópontot választottunk véletlenszer elhelyezéssel a [0, 1] [0, 1] tartományban. Valamennyi csomópont esetén a hatókör sugara r = 0.3. A szimuláció elvégzésére szükség van a szomszédos csomópontok közötti mért távolságokra, amelyek hibáját normál eloszlás segítségével modellezzük. Hasonló eloszlást feltételeztek az [1, 17] cikkekben is. Tehát a mért távolságok és a valós távolságok közötti összefüggések: d kj = d kj (1 + randn() nf), d ij = d ij (1 + randn() nf), ahol randn() a normál eloszlás alapján generált szám, nf pedig a hiba faktor, amelynek értéke 10%. Az el bbi beállítások mellett a lokalizálási feladatot az INTLAB alapú globális optimalizáló eljárás segítségével oldottuk meg. Az eredmény intervallumra 10 3 pontosságot követeltünk meg, és ezen intervallum középpontját tekintettük a keresett szenzorok becsült pozíciójának. Abban az esetben, ha nincs zaj a mért távolságokban, a becsült pozíciók megegyeznek az eredeti pozíciókkal (lásd 1(a) ábra). Zajos távolságok esetén pedig a közelít megoldások az 1(b) ábrán láthatók. Az algoritmus teljes futási ideje a zajos távolságok esetén 261 másodperc. Egy csomópont esetén az átlagos függvény-, gradiens-, illetve Hesse-mátrix kiértékelések száma rendre 194, 139 és 10. A maximális munkalista hossza 10 volt. Az ábrákon látható a csomópontok eredeti pozíciója (karika), a becsült pozíciók (csillag), az eredeti pozíció és a becsült pozíció közötti távolság (vonal), valamint az ismert pozíciójú csomópontok (négyszög). A kapott közelít megoldások javítását, valamint a feladat részletesebb tanulmányozását az X-CSC alapú intervallumos globális optimalizálóval tervezzük.
21 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER (a) Zaj nélküli távolságok (b) Zajos távolságok 1. ábra. A szenzor lokalizációs feladat közelít megoldása zaj nélküli és zajos távolságok esetén 7. Következtetések A cikkben egy intervallumos globális optimalizáló algoritmus új implementációját mutattuk be, és teszteltük azt MATLAB/INTLAB környezetben. Az új programot összehasonlítottuk a hasonló C-XSC alapú eljárással. A teszt eredménye azt mutatta, hogy az új módszer hasonlóan hatékony, mint az el bbi eltekintve a CPU id t l. Megvizsgáltunk továbbá egy új feltételt a Newton-lépés bekapcsolására. Az eredmények alapján ez az új feltétel csökkenti a teljes szükséges számítási id t a régi megoldáshoz viszonyítva. Az INTLAB alapú algoritmus segítségével sikerült jó közelít megoldást találni a szenzor lokalizálási problémára. 8. Köszönetnyilvánítás Az elvégzett kutatást részben a Nemzeti Fejlesztési Ügynökség TÁMOP-4.2.2/ 08/1/ és TÁMOP-4.2.1/B-09/1/KONV pályázatai, valamint az MTA Határon Túli Magyar Tudományos Ösztöndíjprogramja támogatták. Hivatkozások [1] Anderson, B.D.O., Mao, G., and Fidan, B.: Wireless sensor network localization techniques. Computer Networks 51, (2007) [2] Balogh, J., Csendes, T., and Stateva, R.P.: Application of a stochastic method to the solution of the phase stability problem: cubic equations of state. Fluid Phase Equilibria 212, (2003)
22 38 PÁL LÁSZLÓ ÉS CSENDES TIBOR [3] Bánhelyi, B., Csendes, T., and Garay, B.M.: Optimization and the Miranda approach in detecting horseshoe-type chaos by computer. Int. J. Bifurcation and Chaos 17, (2007) [4] Biswas, P. and Ye, Y.: "Semidenite programming for ad hoc wireless sensor network localization", in: Proceedings of the 3-rd International Symposium on Information Processing in Sensor Networks, Berkeley, CA, USA, ACM Press, New York, (2004) [5] Casado, L.G., García, I., and Csendes, T.: A heuristic rejection criterion in interval global optimization algorithms. BIT 41, (2001) [6] Casado, L.G., García, I., Csendes, T., and Ruiz, V.G.: Heuristic Rejection in Interval Global Optimization. J. Optimization Theory and Applications 118, (2003) [7] Csendes, T.: New subinterval selection criteria for interval global optimization. J. Global Optimization 19, (2001) [8] Csendes, T.: Numerical experiences with a new generalized subinterval selection criterion for interval global optimization. Reliable Computing 9, (2003) [9] Csendes, T., Bánhelyi, B., and Hatvani, L.: Towards a computer-assisted proof for chaos in a forced damped pendulum equation. J. Computational and Applied Mathematics 199, (2007) [10] Csendes, T., Garay, B.M., and Bánhelyi, B.: A veried optimization technique to locate chaotic regions of Hénon systems. J. of Global Optimization 35, (2006) [11] Csendes, T., Pál, L., Sendín, J.O.H., and Banga, J.R.: The GLOBAL Optimization Method Revisited. Optimization Letters 2, (2008) [12] Hammer, R., Hocks, M., Kulisch, U., and Ratz, D.: Numerical Toolbox for Veried Computing I. (Springer-Verlag, Berlin, 1993). [13] Kannan, A.A., Mao, G., and Vucetic, B.: Simulated Annealing based Wireless Sensor Network Localization, Journal of Computers 1, (2006) [14] Kearfott, R.B.: Rigorous global search: continuous problems (Kluwer, Dordrecht, 1996). [15] Markót, M.C. and Csendes, T.: A new veried optimization technique for the "packing circles in a unit square" problems. SIAM J. on Optimization 16, (2005) [16] Markót, M.C., Fernández, J., Casado, L.G., and Csendes, T.: New interval methods for constrained global optimization. Mathematical Programming 106, (2006) [17] Niewiadomska-Szynkiewicz, E. and Marks, M.: Optimization Schemes For Wireless Sensor Network Localization. International Journal of Applied Mathematics and Computer Science, 19, (2009) [18] Pál, L. and Csendes, T.: INTLAB implementation of an interval global optimization algorithm. Optimization Methods and Software 24, (2009) [19] Rump, S.M.: INTLAB Interval Laboratory. In: T. Csendes (ed.): Developments in Reliable Computing, Kluwer, Dordrecht, (1999) [20] Szabó, P.G., Markót, M.C., Csendes, T., Specht, E., Casado, L.G., and García, I.: New Approaches to Circle Packing in a Square With Program Codes (Springer-Verlag, Berlin, 2007).
23 EGY INTERVALLUM ALAPÚ GLOBÁLIS OPTIMALIZÁLÁSI MÓDSZER 39 [21] Takács, G.: Helymeghatározás mobiltelefonnal és mobil hálózattal. Híradástechnika 8, (2008) [22] Tóth, B., Fernández, J., and Csendes, T.: Empirical convergence speed of inclusion functions for facility location problems. J. of Computational and Applied Mathematics 199, (2007) [23] Zhang, Q., Wang, J., Jin, C., Ye, J., Ma, C., and Zhang, W.: "Genetic Algorithm Based Wireless Sensor Network Localization", in: Proceedings of the 2008 Fourth International Conference on Natural Computation, (2008) (Beérkezett: május 28.) PÁL LÁSZLÓ Sapientia Erdélyi Magyar Tudományegyetem Gazdaság- és Humántudományok Kar , Csíkszereda, Szabadság tér 1, Románia CSENDES TIBOR Szegedi Tudományegyetem Informatikai Intézet 6720 Szeged, Árpád tér 2. AN INTLAB BASED GLOBAL OPTIMIZATION METHOD AND IT'S APPLICATION TO A SENSOR NETWORK LOCALIZATION PROBLEM László Pál and Tibor Csendes In this paper, we describe a new implementation of an interval optimization algorithm. The algorithm implemented in MATLAB that uses the INTLAB package supporting interval calculations and automatic dierentiation solves the bound constrained global optimization problem. According to the numerical studies completed, the new, INTLAB based implementation is closely as ecient as its C-XSC-based basis algorithm with the exception of the CPU time needed. It can be installed and used easily compared with other similar programs. Furthermore, we examined a new condition for applying the Newton step and we described a sensor network localization problem solved by the INTLAB based algorithm.
Egy intervallum alapú globális optimalizálási módszer és alkalmazása szenzor lokalizálási feladatra
 Egy intervallum alapú globális optimalizálási módszer és alkalmazása szenzor lokalizálási feladatra Pál László és Csendes Tibor Kivonat A cikkben egy intervallum alapú optimalizálási módszer egy új implementációját
Egy intervallum alapú globális optimalizálási módszer és alkalmazása szenzor lokalizálási feladatra Pál László és Csendes Tibor Kivonat A cikkben egy intervallum alapú optimalizálási módszer egy új implementációját
2007. június 8. XXVII. Magyar Operációkutatási Konferencia, Balatonőszöd 1/22. feladatok megoldásában. Csendes Tibor
 2007. június 8. XXVII. Magyar Operációkutatási Konferencia, Balatonőszöd 1/22 Megbízható optimalizálás matematikai feladatok megoldásában Csendes Tibor 2007. június 8. XXVII. Magyar Operációkutatási Konferencia,
2007. június 8. XXVII. Magyar Operációkutatási Konferencia, Balatonőszöd 1/22 Megbízható optimalizálás matematikai feladatok megoldásában Csendes Tibor 2007. június 8. XXVII. Magyar Operációkutatási Konferencia,
Globális optimalizálási algoritmusok intervallum korlátos feladatokra
 Globális optimalizálási algoritmusok intervallum korlátos feladatokra Doktori értekezés tézisei Pál László Témavezet : Dr. Csendes Tibor egyetemi tanár Szegedi Tudományegyetem Informatika Doktori Iskola
Globális optimalizálási algoritmusok intervallum korlátos feladatokra Doktori értekezés tézisei Pál László Témavezet : Dr. Csendes Tibor egyetemi tanár Szegedi Tudományegyetem Informatika Doktori Iskola
Konjugált gradiens módszer
 Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
és alkalmazások, MSc tézis, JATE TTK, Szeged, Témavezető: Dr. Hajnal Péter
 Publikációs jegyzék Balogh János Jegyzetek, tézis: [1] Balogh J., Maximális folyamok és minimális költségű cirkulációk; algoritmusok és alkalmazások, MSc tézis, JATE TTK, Szeged, 1994. Témavezető: Dr.
Publikációs jegyzék Balogh János Jegyzetek, tézis: [1] Balogh J., Maximális folyamok és minimális költségű cirkulációk; algoritmusok és alkalmazások, MSc tézis, JATE TTK, Szeged, 1994. Témavezető: Dr.
Csendes Tibor. Gyakran a gép memóriája is nagy kell hogy legyen. A pontatlanság egyik oka: Adjunk össze 3 számot, majd igazoljuk, hogy ha
 Megbízható számítások Csendes Tibor A cím kissé rejtélyes: a számítógépes algoritmusok a köztudat szerint pontosak és megbízhatók. Az alku során az ügynökök végső érve gyakran az, hogy a kalkulátor is
Megbízható számítások Csendes Tibor A cím kissé rejtélyes: a számítógépes algoritmusok a köztudat szerint pontosak és megbízhatók. Az alku során az ügynökök végső érve gyakran az, hogy a kalkulátor is
Chomsky-féle hierarchia
 http://www.cs.ubbcluj.ro/~kasa/formalis.html Chomsky-féle hierarchia G = (N, T, P, S) nyelvtan: 0-s típusú (általános vagy mondatszerkezet ), ha semmilyen megkötést nem teszünk a helyettesítési szabályaira.
http://www.cs.ubbcluj.ro/~kasa/formalis.html Chomsky-féle hierarchia G = (N, T, P, S) nyelvtan: 0-s típusú (általános vagy mondatszerkezet ), ha semmilyen megkötést nem teszünk a helyettesítési szabályaira.
Végeselem modellezés alapjai 1. óra
 Végeselem modellezés alapjai. óra Gyenge alak, Tesztfüggvény, Lagrange-féle alakfüggvény, Stiness mátrix Kivonat Az óra célja, hogy megismertesse a végeselem módszer (FEM) alkalmazását egy egyszer probléma,
Végeselem modellezés alapjai. óra Gyenge alak, Tesztfüggvény, Lagrange-féle alakfüggvény, Stiness mátrix Kivonat Az óra célja, hogy megismertesse a végeselem módszer (FEM) alkalmazását egy egyszer probléma,
rank(a) == rank([a b])
![rank(a) == rank([a b]) rank(a) == rank([a b])](/thumbs/92/110554624.jpg) Lineáris algebrai egyenletrendszerek megoldása a Matlabban Lineáris algebrai egyenletrendszerek a Matlabban igen egyszer en oldhatók meg. Legyen A az egyenletrendszer m-szer n-es együtthatómátrixa, és
Lineáris algebrai egyenletrendszerek megoldása a Matlabban Lineáris algebrai egyenletrendszerek a Matlabban igen egyszer en oldhatók meg. Legyen A az egyenletrendszer m-szer n-es együtthatómátrixa, és
Függvények július 13. f(x) = 1 x+x 2 f() = 1 ()+() 2 f(f(x)) = 1 (1 x+x 2 )+(1 x+x 2 ) 2 Rendezés után kapjuk, hogy:
 Függvények 015. július 1. 1. Feladat: Határozza meg a következ összetett függvényeket! f(x) = cos x + x g(x) = x f(g(x)) =? g(f(x)) =? Megoldás: Összetett függvény el állításához a küls függvényben a független
Függvények 015. július 1. 1. Feladat: Határozza meg a következ összetett függvényeket! f(x) = cos x + x g(x) = x f(g(x)) =? g(f(x)) =? Megoldás: Összetett függvény el állításához a küls függvényben a független
Heurisztikák BitTorrent hálózatok max-min méltányos sávszélesség-kiosztására
 Heurisztikák BitTorrent hálózatok max-min méltányos sávszélesség-kiosztására Dobjánné Antal Elvira és Vinkó Tamás Pallasz Athéné Egyetem, GAMF M szaki és Informatikai Kar Szegedi Tudományegyetem, Informatikai
Heurisztikák BitTorrent hálózatok max-min méltányos sávszélesség-kiosztására Dobjánné Antal Elvira és Vinkó Tamás Pallasz Athéné Egyetem, GAMF M szaki és Informatikai Kar Szegedi Tudományegyetem, Informatikai
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2018/
 Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Opkut deníciók és tételek
 Opkut deníciók és tételek Készítette: Bán József Deníciók 1. Deníció (Lineáris programozási feladat). Keressük meg adott lineáris, R n értelmezési tartományú függvény, az ún. célfüggvény széls értékét
Opkut deníciók és tételek Készítette: Bán József Deníciók 1. Deníció (Lineáris programozási feladat). Keressük meg adott lineáris, R n értelmezési tartományú függvény, az ún. célfüggvény széls értékét
MÉLYFÚRÁSI GEOFIZIKAI ADATOK ÉRTELMEZÉSÉNEK MODERN INVERZIÓS MÓDSZEREI
 MIKOVINY SÁMUEL FÖLDTUDOMÁNYI DOKTORI ISKOLA Doktori értekezés tézisei MÉLYFÚRÁSI GEOFIZIKAI ADATOK ÉRTELMEZÉSÉNEK MODERN INVERZIÓS MÓDSZEREI Írta: SZABÓ NORBERT PÉTER Tudományos vezető: DR. DOBRÓKA MIHÁLY
MIKOVINY SÁMUEL FÖLDTUDOMÁNYI DOKTORI ISKOLA Doktori értekezés tézisei MÉLYFÚRÁSI GEOFIZIKAI ADATOK ÉRTELMEZÉSÉNEK MODERN INVERZIÓS MÓDSZEREI Írta: SZABÓ NORBERT PÉTER Tudományos vezető: DR. DOBRÓKA MIHÁLY
SCILAB programcsomag segítségével
 Felhasználói függvények de niálása és függvények 3D ábrázolása SCILAB programcsomag segítségével 1. Felhasználói függvények de niálása A Scilab programcsomag rengeteg matematikai függvényt biztosít a számítások
Felhasználói függvények de niálása és függvények 3D ábrázolása SCILAB programcsomag segítségével 1. Felhasználói függvények de niálása A Scilab programcsomag rengeteg matematikai függvényt biztosít a számítások
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
értékel függvény: rátermettségi függvény (tness function)
 Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Taylor-polinomok. 1. Alapfeladatok. 2015. április 11. 1. Feladat: Írjuk fel az f(x) = e 2x függvény másodfokú Maclaurinpolinomját!
 Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
Előrenéző és paraméter tanuló algoritmusok on-line klaszterezési problémákra
 Szegedi Tudományegyetem Számítógépes Algoritmusok és Mesterséges Intelligencia Tanszék Dr. Németh Tamás Előrenéző és paraméter tanuló algoritmusok on-line klaszterezési problémákra SZTE TTIK, Móra Kollégium,
Szegedi Tudományegyetem Számítógépes Algoritmusok és Mesterséges Intelligencia Tanszék Dr. Németh Tamás Előrenéző és paraméter tanuló algoritmusok on-line klaszterezési problémákra SZTE TTIK, Móra Kollégium,
értékel függvény: rátermettségi függvény (tness function)
 Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Genetikus algoritmusok globális optimalizálás sok lehetséges megoldás közül keressük a legjobbat értékel függvény: rátermettségi függvény (tness function) populáció kiválasztjuk a legrátermettebb egyedeket
Algoritmusok bonyolultsága
 Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel p. 1/29. Ábele-Nagy Kristóf BCE, ELTE
 Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel Ábele-Nagy Kristóf BCE, ELTE Bozóki Sándor BCE, MTA SZTAKI 2010. november 4. Nem teljesen kitöltött páros
Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel Ábele-Nagy Kristóf BCE, ELTE Bozóki Sándor BCE, MTA SZTAKI 2010. november 4. Nem teljesen kitöltött páros
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Egyváltozós függvények 1.
 Egyváltozós függvények 1. Filip Ferdinánd filip.ferdinand@bgk.uni-obuda.hu siva.banki.hu/jegyzetek 015 szeptember 1. Filip Ferdinánd 015 szeptember 1. Egyváltozós függvények 1. 1 / 5 Az el adás vázlata
Egyváltozós függvények 1. Filip Ferdinánd filip.ferdinand@bgk.uni-obuda.hu siva.banki.hu/jegyzetek 015 szeptember 1. Filip Ferdinánd 015 szeptember 1. Egyváltozós függvények 1. 1 / 5 Az el adás vázlata
Matematikai programok
 Matematikai programok Mátrixalapú nyelvek MatLab Wettl Ferenc diái alapján Budapesti M szaki Egyetem Algebra Tanszék 2017.11.07 Borbély Gábor (BME Algebra Tanszék) Matematikai programok 2017.11.07 1 /
Matematikai programok Mátrixalapú nyelvek MatLab Wettl Ferenc diái alapján Budapesti M szaki Egyetem Algebra Tanszék 2017.11.07 Borbély Gábor (BME Algebra Tanszék) Matematikai programok 2017.11.07 1 /
Gauss-Jordan módszer Legkisebb négyzetek módszere, egyenes LNM, polinom LNM, függvény. Lineáris algebra numerikus módszerei
 A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
Online algoritmusok. Algoritmusok és bonyolultságuk. Horváth Bálint március 30. Horváth Bálint Online algoritmusok március 30.
 Online algoritmusok Algoritmusok és bonyolultságuk Horváth Bálint 2018. március 30. Horváth Bálint Online algoritmusok 2018. március 30. 1 / 28 Motiváció Gyakran el fordul, hogy a bemenetet csak részenként
Online algoritmusok Algoritmusok és bonyolultságuk Horváth Bálint 2018. március 30. Horváth Bálint Online algoritmusok 2018. március 30. 1 / 28 Motiváció Gyakran el fordul, hogy a bemenetet csak részenként
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
MATLAB alapismeretek I.
 Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek I. A MATLAB bemutatása MATLAB filozófia MATLAB modulok A MATLAB felhasználói felülete MATLAB tulajdonságok
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek I. A MATLAB bemutatása MATLAB filozófia MATLAB modulok A MATLAB felhasználói felülete MATLAB tulajdonságok
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 8. Előadás Dr. Kulcsár Gyula egyetemi docens Kereső algoritmusok alkalmazása
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 8. Előadás Dr. Kulcsár Gyula egyetemi docens Kereső algoritmusok alkalmazása
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Funkcionális és logikai programozás. { Márton Gyöngyvér, 2012} { Sapientia, Erdélyi Magyar Tudományegyetem }
 Funkcionális és logikai programozás { Márton Gyöngyvér, 2012} { Sapientia, Erdélyi Magyar Tudományegyetem } http://www.ms.sapientia.ro/~mgyongyi ` 1 Jelenlét: Követelmények, osztályozás Az első 4 előadáson
Funkcionális és logikai programozás { Márton Gyöngyvér, 2012} { Sapientia, Erdélyi Magyar Tudományegyetem } http://www.ms.sapientia.ro/~mgyongyi ` 1 Jelenlét: Követelmények, osztályozás Az első 4 előadáson
Dr. habil. Maróti György
 infokommunikációs technológiák III.8. MÓDSZER KIDOLGOZÁSA ALGORITMUSOK ÁTÜLTETÉSÉRE KIS SZÁMÍTÁSI TELJESÍTMÉNYŰ ESZKÖZÖKBŐL ÁLLÓ NÉPES HETEROGÉN INFRASTRUKTÚRA Dr. habil. Maróti György maroti@dcs.uni-pannon.hu
infokommunikációs technológiák III.8. MÓDSZER KIDOLGOZÁSA ALGORITMUSOK ÁTÜLTETÉSÉRE KIS SZÁMÍTÁSI TELJESÍTMÉNYŰ ESZKÖZÖKBŐL ÁLLÓ NÉPES HETEROGÉN INFRASTRUKTÚRA Dr. habil. Maróti György maroti@dcs.uni-pannon.hu
Egy késleltetett differenciálegyenlet vizsgálata megbízható számítógépes eljárással
 Egy késleltetett differenciálegyenlet vizsgálata megbízható számítógépes eljárással Bánhelyi Balázs Szeged Kivonat A szakirodalomban nem volt ismert megbízható numerikus eljárás késleltetett differenciálegyenletek
Egy késleltetett differenciálegyenlet vizsgálata megbízható számítógépes eljárással Bánhelyi Balázs Szeged Kivonat A szakirodalomban nem volt ismert megbízható numerikus eljárás késleltetett differenciálegyenletek
Programozási módszertan. Mohó algoritmusok
 PM-08 p. 1/17 Programozási módszertan Mohó algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu PM-08 p. 2/17 Bevezetés Dinamikus programozás
PM-08 p. 1/17 Programozási módszertan Mohó algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu PM-08 p. 2/17 Bevezetés Dinamikus programozás
MATLAB OKTATÁS 5. ELŐADÁS FELTÉTEL NÉLKÜLI ÉS FELTÉTELES OPTIMALIZÁLÁS. Dr. Bécsi Tamás Hegedüs Ferenc
 MATLAB OKTATÁS 5. ELŐADÁS FELTÉTEL NÉLKÜLI ÉS FELTÉTELES OPTIMALIZÁLÁS Dr. Bécsi Tamás Hegedüs Ferenc FELTÉTEL NÉLKÜLI OPTIMALIZÁLÁS (FMINSEARCH) Feltétel nélküli optimalizálásra a MATLAB az fminsearch
MATLAB OKTATÁS 5. ELŐADÁS FELTÉTEL NÉLKÜLI ÉS FELTÉTELES OPTIMALIZÁLÁS Dr. Bécsi Tamás Hegedüs Ferenc FELTÉTEL NÉLKÜLI OPTIMALIZÁLÁS (FMINSEARCH) Feltétel nélküli optimalizálásra a MATLAB az fminsearch
Vektorterek. Wettl Ferenc február 17. Wettl Ferenc Vektorterek február / 27
 Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
MATE-INFO UBB verseny, március 25. MATEMATIKA írásbeli vizsga
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
Operációs rendszerek. 11. gyakorlat. AWK - szintaxis, vezérlési szerkezetek UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED
 UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED AWK - szintaxis, vezérlési szerkezetek Operációs rendszerek 11. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Csuvik
UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED AWK - szintaxis, vezérlési szerkezetek Operációs rendszerek 11. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Csuvik
Felvételi tematika INFORMATIKA
 Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
A MATLAB alapjai. Kezdő lépések. Változók. Aktuális mappa Parancs ablak. Előzmények. Részei. Atomerőművek üzemtana
 A MATLAB alapjai Kezdő lépések - Matlab Promt: >> - Help: >> help sqrt >> doc sqrt - Kilépés: >> quit >> exit >> Futó script leállítása: >> ctrl+c - Változók listásása >> who >> whos - Változók törlése
A MATLAB alapjai Kezdő lépések - Matlab Promt: >> - Help: >> help sqrt >> doc sqrt - Kilépés: >> quit >> exit >> Futó script leállítása: >> ctrl+c - Változók listásása >> who >> whos - Változók törlése
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Tartalom Keresés és rendezés. Vektoralgoritmusok. 1. fejezet. Keresés adatvektorban. A programozás alapjai I.
 Keresés Rendezés Feladat Keresés Rendezés Feladat Tartalom Keresés és rendezés A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán
Keresés Rendezés Feladat Keresés Rendezés Feladat Tartalom Keresés és rendezés A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán
Függvények növekedési korlátainak jellemzése
 17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
end function Az A vektorban elõforduló legnagyobb és legkisebb értékek indexeinek különbségét.. (1.5 pont) Ha üres a vektor, akkor 0-t..
 A Név: l 2014.04.09 Neptun kód: Gyakorlat vezető: HG BP MN l 1. Adott egy (12 nem nulla értékû elemmel rendelkezõ) 6x7 méretû ritka mátrix hiányos 4+2 soros reprezentációja. SOR: 1 1 2 2 2 3 3 4 4 5 6
A Név: l 2014.04.09 Neptun kód: Gyakorlat vezető: HG BP MN l 1. Adott egy (12 nem nulla értékû elemmel rendelkezõ) 6x7 méretû ritka mátrix hiányos 4+2 soros reprezentációja. SOR: 1 1 2 2 2 3 3 4 4 5 6
Robotok inverz geometriája
 Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
0,424 0,576. f) P (X 2 = 3) g) P (X 3 = 1) h) P (X 4 = 1 vagy 2 X 2 = 2) i) P (X 7 = 3, X 4 = 1, X 2 = 2 X 0 = 2) j) P (X 7 = 3, X 4 = 1, X 2 = 2)
 Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
3. Lineáris differenciálegyenletek
 3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
2. SZÉLSŽÉRTÉKSZÁMÍTÁS. 2.1 A széls érték fogalma, létezése
 2 SZÉLSŽÉRTÉKSZÁMÍTÁS DEFINÍCIÓ 21 A széls érték fogalma, létezése Azt mondjuk, hogy az f : D R k R függvénynek lokális (helyi) maximuma (minimuma) van az x 0 D pontban, ha van olyan ε > 0 hogy f(x 0 )
2 SZÉLSŽÉRTÉKSZÁMÍTÁS DEFINÍCIÓ 21 A széls érték fogalma, létezése Azt mondjuk, hogy az f : D R k R függvénynek lokális (helyi) maximuma (minimuma) van az x 0 D pontban, ha van olyan ε > 0 hogy f(x 0 )
Osztott jáva programok automatikus tesztelése. Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január
 Osztott jáva programok automatikus tesztelése Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január Osztott alkalmazások Automatikus tesztelés Tesztelés heurisztikus zaj keltés Tesztelés genetikus
Osztott jáva programok automatikus tesztelése Matkó Imre BBTE, Kolozsvár Informatika szak, IV. Év 2007 január Osztott alkalmazások Automatikus tesztelés Tesztelés heurisztikus zaj keltés Tesztelés genetikus
Lineáris leképezések. Wettl Ferenc március 9. Wettl Ferenc Lineáris leképezések március 9. 1 / 31
 Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Keresés és rendezés. A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán
 Keresés Rendezés Feladat Keresés és rendezés A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán 2016. november 7. Farkas B., Fiala
Keresés Rendezés Feladat Keresés és rendezés A programozás alapjai I. Hálózati Rendszerek és Szolgáltatások Tanszék Farkas Balázs, Fiala Péter, Vitéz András, Zsóka Zoltán 2016. november 7. Farkas B., Fiala
Nem-lineáris programozási feladatok
 Nem-lineáris programozási feladatok S - lehetséges halmaz 2008.02.04 Dr.Bajalinov Erik, NyF MII 1 Elég egyszerű példa: nemlineáris célfüggvény + lineáris feltételek Lehetséges halmaz x 1 *x 2 =6.75 Gradiens
Nem-lineáris programozási feladatok S - lehetséges halmaz 2008.02.04 Dr.Bajalinov Erik, NyF MII 1 Elég egyszerű példa: nemlineáris célfüggvény + lineáris feltételek Lehetséges halmaz x 1 *x 2 =6.75 Gradiens
Numerikus integrálás
 Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Gyakorló feladatok. Agbeko Kwami Nutefe és Nagy Noémi
 Gyakorló feladatok Agbeko Kwami Nutefe és Nagy Noémi 25 Tartalomjegyzék. Klasszikus hibaszámítás 3 2. Lineáris egyenletrendszerek 3 3. Interpoláció 4 4. Sajátérték, sajátvektor 6 5. Lineáris és nemlineáris
Gyakorló feladatok Agbeko Kwami Nutefe és Nagy Noémi 25 Tartalomjegyzék. Klasszikus hibaszámítás 3 2. Lineáris egyenletrendszerek 3 3. Interpoláció 4 4. Sajátérték, sajátvektor 6 5. Lineáris és nemlineáris
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel
 Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
VALÓSZÍNŰSÉG MAXIMALIZÁLÁS PROBABILITY MAXIMIZATION
 Gradus Vol 5, No 1 (2018) 128-133 ISSN 2064-8014 VALÓSZÍNŰSÉG MAXIMALIZÁLÁS PROBABILITY MAXIMIZATION Csizmás Edit 1*, Drenyovszki Rajmund 1, Vajnai Tibor 1, Kovács Lóránt 1, Fábián Csaba 1 1 Informatika
Gradus Vol 5, No 1 (2018) 128-133 ISSN 2064-8014 VALÓSZÍNŰSÉG MAXIMALIZÁLÁS PROBABILITY MAXIMIZATION Csizmás Edit 1*, Drenyovszki Rajmund 1, Vajnai Tibor 1, Kovács Lóránt 1, Fábián Csaba 1 1 Informatika
Programozás. (GKxB_INTM021) Dr. Hatwágner F. Miklós március 31. Széchenyi István Egyetem, Gy r
 Programozás (GKxB_INTM021) Széchenyi István Egyetem, Gy r 2018. március 31. Városok közötti távolság Feladat: két város nevének beolvasása, városok közötti távolság megjelenítése. Kilépés azonos városok
Programozás (GKxB_INTM021) Széchenyi István Egyetem, Gy r 2018. március 31. Városok közötti távolság Feladat: két város nevének beolvasása, városok közötti távolság megjelenítése. Kilépés azonos városok
4. Használati útmutatás
 megbízható(másnéven: robusztus): mert a programozási hibák egy részét megakadályozza,a másik részét pedig futás közben kisz ri és támogatja a fejleszt t azok professzionális kezelésében. biztonságos: megakadályozza
megbízható(másnéven: robusztus): mert a programozási hibák egy részét megakadályozza,a másik részét pedig futás közben kisz ri és támogatja a fejleszt t azok professzionális kezelésében. biztonságos: megakadályozza
Skalárszorzat, norma, szög, távolság. Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2005.
 1 Diszkrét matematika II., 4. el adás Skalárszorzat, norma, szög, távolság Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2005. március 1 A téma jelent sége
1 Diszkrét matematika II., 4. el adás Skalárszorzat, norma, szög, távolság Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2005. március 1 A téma jelent sége
Chomsky-féle hierarchia
 http://www.ms.sapientia.ro/ kasa/formalis.htm Chomsky-féle hierarchia G = (N, T, P, S) nyelvtan: 0-s típusú (általános vagy mondatszerkezetű), ha semmilyen megkötést nem teszünk a helyettesítési szabályaira.
http://www.ms.sapientia.ro/ kasa/formalis.htm Chomsky-féle hierarchia G = (N, T, P, S) nyelvtan: 0-s típusú (általános vagy mondatszerkezetű), ha semmilyen megkötést nem teszünk a helyettesítési szabályaira.
Mádi-Nagy Gergely * A feladat pontos leírása. Tekintsünk darab tetszõleges eseményt, jelöljük ezeket a következõképpen: ,...,
 Mádi-Nagy Gergely * AZ ESEMÉNYEK UNIÓJÁNAK VALÓSZÍNÛSÉGE BECSLÉS A TÖBBVÁLTOZÓS DISZKRÉT MOMENTUM PROBLÉMA SEGÍTSÉGÉVEL Az események uniója valószínûsége becslésére szolgáló elsõ fontos eredmények a Boole-
Mádi-Nagy Gergely * AZ ESEMÉNYEK UNIÓJÁNAK VALÓSZÍNÛSÉGE BECSLÉS A TÖBBVÁLTOZÓS DISZKRÉT MOMENTUM PROBLÉMA SEGÍTSÉGÉVEL Az események uniója valószínûsége becslésére szolgáló elsõ fontos eredmények a Boole-
Intervallum Módszerek Alkalmazása Vegyészmérnöki Számításokban. Tézisfüzet
 BUDAPESTI MŐSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VEGYÉSZMÉRNÖKI ÉS BIOMÉRNÖKI KAR OLÁH GYÖRGY DOKTORI ISKOLA Intervallum Módszerek Alkalmazása Vegyészmérnöki Számításokban Tézisfüzet Szerzı: Baharev Ali,
BUDAPESTI MŐSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VEGYÉSZMÉRNÖKI ÉS BIOMÉRNÖKI KAR OLÁH GYÖRGY DOKTORI ISKOLA Intervallum Módszerek Alkalmazása Vegyészmérnöki Számításokban Tézisfüzet Szerzı: Baharev Ali,
A függvény kód szekvenciáját kapcsos zárójelek közt definiáljuk, a { } -ek közti részt a Bash héj kód blokknak (code block) nevezi.
 Függvények 1.Függvények...1 1.1.A függvény deníció szintaxisa... 1..Függvények érték visszatérítése...3 1.3.Környezettel kapcsolatos kérdések...4 1.4.Lokális változók használata...4 1.5.Rekurzív hívások...5.kód
Függvények 1.Függvények...1 1.1.A függvény deníció szintaxisa... 1..Függvények érték visszatérítése...3 1.3.Környezettel kapcsolatos kérdések...4 1.4.Lokális változók használata...4 1.5.Rekurzív hívások...5.kód
Haladók III. kategória 2. (dönt ) forduló
 Haladók III. kategória 2. (dönt ) forduló 1. Tetsz leges n pozitív egész számra jelölje f (n) az olyan 2n-jegy számok számát, amelyek megegyeznek az utolsó n számjegyükb l alkotott szám négyzetével. Határozzuk
Haladók III. kategória 2. (dönt ) forduló 1. Tetsz leges n pozitív egész számra jelölje f (n) az olyan 2n-jegy számok számát, amelyek megegyeznek az utolsó n számjegyükb l alkotott szám négyzetével. Határozzuk
2. Visszalépéses stratégia
 2. Visszalépéses stratégia A visszalépéses keres rendszer olyan KR, amely globális munkaterülete: út a startcsúcsból az aktuális csúcsba (ezen kívül a még ki nem próbált élek nyilvántartása) keresés szabályai:
2. Visszalépéses stratégia A visszalépéses keres rendszer olyan KR, amely globális munkaterülete: út a startcsúcsból az aktuális csúcsba (ezen kívül a még ki nem próbált élek nyilvántartása) keresés szabályai:
1. Olvassuk be két pont koordinátáit: (x1, y1) és (x2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki.
 Számítás:. Olvassuk be két pont koordinátáit: (, y) és (2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki. 2. Olvassuk be két darab két dimenziós vektor komponenseit: (a, ay) és (b, by). Határozzuk
Számítás:. Olvassuk be két pont koordinátáit: (, y) és (2, y2). Határozzuk meg a két pont távolságát és nyomtassuk ki. 2. Olvassuk be két darab két dimenziós vektor komponenseit: (a, ay) és (b, by). Határozzuk
A derivált alkalmazásai
 A derivált alkalmazásai Összeállította: Wettl Ferenc 2014. november 17. Wettl Ferenc A derivált alkalmazásai 2014. november 17. 1 / 57 Tartalom 1 Függvény széls értékei Abszolút széls értékek Lokális széls
A derivált alkalmazásai Összeállította: Wettl Ferenc 2014. november 17. Wettl Ferenc A derivált alkalmazásai 2014. november 17. 1 / 57 Tartalom 1 Függvény széls értékei Abszolút széls értékek Lokális széls
Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit.
 2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
Nemlineáris optimalizálási problémák párhuzamos megoldása grafikus processzorok felhasználásával
 Nemlineáris optimalizálási problémák párhuzamos megoldása grafikus processzorok felhasználásával 1 1 Eötvös Loránd Tudományegyetem, Informatikai Kar Kari TDK, 2016. 05. 10. Tartalom 1 2 Tartalom 1 2 Optimalizálási
Nemlineáris optimalizálási problémák párhuzamos megoldása grafikus processzorok felhasználásával 1 1 Eötvös Loránd Tudományegyetem, Informatikai Kar Kari TDK, 2016. 05. 10. Tartalom 1 2 Tartalom 1 2 Optimalizálási
EGY KÉSLELTETETT DIFFERENCIÁLEGYENLET VIZSGÁLATA MEGBÍZHATÓ SZÁMÍTÓGÉPES ELJÁRÁSSAL. 1. Bevezetés
 Alkalmazott Matematikai Lapok 24 (2007), 131-150. EGY KÉSLELTETETT DIFFERENCIÁLEGYENLET VIZSGÁLATA MEGBÍZHATÓ SZÁMÍTÓGÉPES ELJÁRÁSSAL BÁNHELYI BALÁZS A szakirodalomban nem volt ismert megbízható numerikus
Alkalmazott Matematikai Lapok 24 (2007), 131-150. EGY KÉSLELTETETT DIFFERENCIÁLEGYENLET VIZSGÁLATA MEGBÍZHATÓ SZÁMÍTÓGÉPES ELJÁRÁSSAL BÁNHELYI BALÁZS A szakirodalomban nem volt ismert megbízható numerikus
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai 1.
 Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai.). Feladat. Határozzuk meg az alábbi integrálokat: a) x x + dx d) xe x dx b) c)
Feladatok megoldásokkal a 9. gyakorlathoz (Newton-Leibniz formula, közelítő integrálás, az integrálszámítás alkalmazásai.). Feladat. Határozzuk meg az alábbi integrálokat: a) x x + dx d) xe x dx b) c)
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 5. Előadás Dr. Kulcsár Gyula egyetemi docens Tartalom 1. Párhuzamosan
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 5. Előadás Dr. Kulcsár Gyula egyetemi docens Tartalom 1. Párhuzamosan
Sorozatok és Sorozatok és / 18
 Sorozatok 2015.11.30. és 2015.12.02. Sorozatok 2015.11.30. és 2015.12.02. 1 / 18 Tartalom 1 Sorozatok alapfogalmai 2 Sorozatok jellemz i 3 Sorozatok határértéke 4 Konvergencia és korlátosság 5 Cauchy-féle
Sorozatok 2015.11.30. és 2015.12.02. Sorozatok 2015.11.30. és 2015.12.02. 1 / 18 Tartalom 1 Sorozatok alapfogalmai 2 Sorozatok jellemz i 3 Sorozatok határértéke 4 Konvergencia és korlátosság 5 Cauchy-féle
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Amortizációs költségelemzés
 Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Nagyságrendek. Kiegészítő anyag az Algoritmuselmélet tárgyhoz. Friedl Katalin BME SZIT február 1.
 Nagyságrendek Kiegészítő anyag az Algoritmuselmélet tárgyhoz (a Rónyai Ivanyos Szabó: Algoritmusok könyv mellé) Friedl Katalin BME SZIT friedl@cs.bme.hu 018. február 1. Az O, Ω, Θ jelölések Az algoritmusok
Nagyságrendek Kiegészítő anyag az Algoritmuselmélet tárgyhoz (a Rónyai Ivanyos Szabó: Algoritmusok könyv mellé) Friedl Katalin BME SZIT friedl@cs.bme.hu 018. február 1. Az O, Ω, Θ jelölések Az algoritmusok
10. Előadás. 1. Feltétel nélküli optimalizálás: Az eljárás alapjai
 Optimalizálási eljárások MSc hallgatók számára 10. Előadás Előadó: Hajnal Péter Jegyzetelő: T. Szabó Tamás 2011. április 20. 1. Feltétel nélküli optimalizálás: Az eljárás alapjai A feltétel nélküli optimalizálásnál
Optimalizálási eljárások MSc hallgatók számára 10. Előadás Előadó: Hajnal Péter Jegyzetelő: T. Szabó Tamás 2011. április 20. 1. Feltétel nélküli optimalizálás: Az eljárás alapjai A feltétel nélküli optimalizálásnál
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével
 Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Konvex optimalizálás feladatok
 (1. gyakorlat, 2014. szeptember 16.) 1. Feladat. Mutassuk meg, hogy az f : R R, f(x) := x 2 függvény konvex (a másodrend derivált segítségével, illetve deníció szerint is)! 2. Feladat. Mutassuk meg, hogy
(1. gyakorlat, 2014. szeptember 16.) 1. Feladat. Mutassuk meg, hogy az f : R R, f(x) := x 2 függvény konvex (a másodrend derivált segítségével, illetve deníció szerint is)! 2. Feladat. Mutassuk meg, hogy
2. Visszalépéses keresés
 2. Visszalépéses keresés Visszalépéses keresés A visszalépéses keresés egy olyan KR, amely globális munkaterülete: egy út a startcsúcsból az aktuális csúcsba (az útról leágazó még ki nem próbált élekkel
2. Visszalépéses keresés Visszalépéses keresés A visszalépéses keresés egy olyan KR, amely globális munkaterülete: egy út a startcsúcsból az aktuális csúcsba (az útról leágazó még ki nem próbált élekkel
3. el adás: Determinánsok
 3. el adás: Determinánsok Wettl Ferenc 2015. február 27. Wettl Ferenc 3. el adás: Determinánsok 2015. február 27. 1 / 19 Tartalom 1 Motiváció 2 A determináns mint sorvektorainak függvénye 3 A determináns
3. el adás: Determinánsok Wettl Ferenc 2015. február 27. Wettl Ferenc 3. el adás: Determinánsok 2015. február 27. 1 / 19 Tartalom 1 Motiváció 2 A determináns mint sorvektorainak függvénye 3 A determináns
Hidraulikus hálózatok robusztusságának növelése
 Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Osztott algoritmusok
 Osztott algoritmusok A benzinkutas példa szimulációja Müller Csaba 2010. december 4. 1. Bevezetés Első lépésben talán kezdjük a probléma ismertetésével. Adott két n hosszúságú bináris sorozat (s 1, s 2
Osztott algoritmusok A benzinkutas példa szimulációja Müller Csaba 2010. december 4. 1. Bevezetés Első lépésben talán kezdjük a probléma ismertetésével. Adott két n hosszúságú bináris sorozat (s 1, s 2
Optimalizálás alapfeladata Legmeredekebb lejtő Lagrange függvény Log-barrier módszer Büntetőfüggvény módszer 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Sztojka Miroszláv LINEÁRIS ALGEBRA Egyetemi jegyzet Ungvár 2013
 UKRAJNA OKTATÁSI ÉS TUDOMÁNYÜGYI MINISZTÉRIUMA ÁLLAMI FELSŐOKTATÁSI INTÉZMÉNY UNGVÁRI NEMZETI EGYETEM MAGYAR TANNYELVŰ HUMÁN- ÉS TERMÉSZETTUDOMÁNYI KAR FIZIKA ÉS MATEMATIKA TANSZÉK Sztojka Miroszláv LINEÁRIS
UKRAJNA OKTATÁSI ÉS TUDOMÁNYÜGYI MINISZTÉRIUMA ÁLLAMI FELSŐOKTATÁSI INTÉZMÉNY UNGVÁRI NEMZETI EGYETEM MAGYAR TANNYELVŰ HUMÁN- ÉS TERMÉSZETTUDOMÁNYI KAR FIZIKA ÉS MATEMATIKA TANSZÉK Sztojka Miroszláv LINEÁRIS
Publikációs lista. Dr. Molnárka-Miletics Edit Széchenyi István Egyetem Matematika és Számítástudományi Tanszék
 Publikációs lista Dr. Molnárka-Miletics Edit Széchenyi István Egyetem Matematika és Számítástudományi Tanszék Folyóirat cikkek: E. Miletics: Energy conservative algorithm for numerical solution of ODEs
Publikációs lista Dr. Molnárka-Miletics Edit Széchenyi István Egyetem Matematika és Számítástudományi Tanszék Folyóirat cikkek: E. Miletics: Energy conservative algorithm for numerical solution of ODEs
Megoldott feladatok november 30. n+3 szigorúan monoton csökken, 5. n+3. lim a n = lim. n+3 = 2n+3 n+4 2n+1
 Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Gépi tanulás a gyakorlatban. Lineáris regresszió
 Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Sztochasztikus optimalizálás tehenészetben
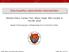 Sztochasztikus optimalizálás tehenészetben Bánhelyi Balázs, Csendes Tibor, Mester Abigél, Mikó Józsefné és Horváth József Szegedi Tudományegyetem, Mezőgazdasági Kar és Informatikai Intézet Anyag Több tehenészetet
Sztochasztikus optimalizálás tehenészetben Bánhelyi Balázs, Csendes Tibor, Mester Abigél, Mikó Józsefné és Horváth József Szegedi Tudományegyetem, Mezőgazdasági Kar és Informatikai Intézet Anyag Több tehenészetet
Módszer köztes tárolókat nem tartalmazó szakaszos működésű rendszerek ütemezésére
 Módszer köztes tárolókat nem tartalmazó szakaszos működésű rendszerek ütemezésére Doktori (PhD) értekezés tézisei Holczinger Tibor Témavezető: Dr. Friedler Ferenc Veszprémi Egyetem Műszaki Informatikai
Módszer köztes tárolókat nem tartalmazó szakaszos működésű rendszerek ütemezésére Doktori (PhD) értekezés tézisei Holczinger Tibor Témavezető: Dr. Friedler Ferenc Veszprémi Egyetem Műszaki Informatikai
Dinamikus programozás vagy Oszd meg, és uralkodj!
 Dinamikus programozás Oszd meg, és uralkodj! Mohó stratégia Melyiket válasszuk? Dinamikus programozás vagy Oszd meg, és uralkodj! Háromszögfeladat rekurzívan: c nj := a nj ha 1 j n c ij := a ij + max{c
Dinamikus programozás Oszd meg, és uralkodj! Mohó stratégia Melyiket válasszuk? Dinamikus programozás vagy Oszd meg, és uralkodj! Háromszögfeladat rekurzívan: c nj := a nj ha 1 j n c ij := a ij + max{c
Matematikai programok
 Matematikai programok Mátrixalapú nyelvek octave Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Wettl
Matematikai programok Mátrixalapú nyelvek octave Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Wettl
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Közösség detektálás gráfokban
 Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
