A pénzügyi kockázat mérése és kezelése
|
|
|
- Etelka Fekete
- 8 évvel ezelőtt
- Látták:
Átírás
1 A pénzügyi kockázat mérése és kezelése Varga-Haszonits István Gazdasági Fizika Téli Iskola, január 31.
2 Áttekintés 1 Bevezetés 2 A portfólióválasztási probléma 3 Kockázati mértékek 4 A hatékony portfóliók becslése 5 További érdekes témák
3 Mi a kockázat? Intuitíve érezzük a választ. Megfogalmazni mégsem könnyű. Hát még mérni! És akkor még nem is kezeltük...
4 Melyik kockázatosabb? Képzeljünk el két különböző befektetést, A-t és B-t. Mindkettőbe 1000Ft-ért lehet beszállni. 1 év múlva: 1 az A befektetés garantáltan 1100Ft-ot fizet, 2 a B befektetés 50%-50% eséllyel 1000 vagy 1300Ft-ot fizet. Melyik a jobb üzlet? Melyik a kockázatosabb üzlet?
5 Melyik kockázatosabb? Képzeljünk el két másik befektetést, C-t és D-t. C és D ismét 1000Ft kezdőtőkét igényel. 1 év múlva: 1 C 50-50% eséllyel 500, illetve 1500Ft-ot fizet, 2 D % eséllyel 500, 1500, illetve 2000Ft-ot fizet. Melyik a jobb üzlet? Melyik a kockázatosabb üzlet?
6 Melyik kockázatosabb? Képzeljünk el két újabb befektetést, E-t és F-t. E és F ára szintén 1000Ft. 1 év múlva: 1 E 50-50% eséllyel 1000, illetve 1200Ft-ot fizet, 2 D % eséllyel -200, 1000, 1200 illetve 3000Ft-ot fizet. Melyik a jobb üzlet? Melyik a kockázatosabb üzlet?
7 Miben nyilvánul meg a kockázat? A végkifejlet pontosan nem ismert. Előfordulhat, hogy a végén kevesebb marad, mint amennyivel indulunk. Előfordulhat, hogy a befektetett pénzből semmi sem marad. Még az is megeshet, hogy adósok börtönébe kerülünk. Sőt, még azt sem tudhatjuk biztosan, hogy tisztában vagyunk-e a lehetséges kimenetelekkel.
8 Honnan ered a kockázat? Felmerül a kérdés, honnan származik a pénzügyi kockázat. Egy megszokott csoportosítás: Piaci kockázat Likviditási kockázat Hitelkockázat Működési kockázat Jogi/szabályozási kockázat Valójában a fenti kategóriák nehezen elkülöníthetők.
9 Hogyan mérjük a kockázatot? A befektetések értéke/hozama valószínűségi változóként/sztochasztikus folyamatként modellezhető. A hozamok eloszlása tehát elvileg mindent elmond a kockázatról. Az információ ebben a formában azonban túl implicit, nehezen értelmezhető. Szeretnénk tehát valamiféle mérőszámot rendelni a kockázathoz. A kockázat ilyen értelemben az eloszlás valamilyen funkcionálja. A megfelelő funkcionál kiválasztása a kockázat elméletének legfontosabb, és talán legnehezebb problémája.
10 Hogyan becsüljük a kockázatot? A pénzügyi folyamatok eloszlását a gyakorlatban nem ismerjük. Így a jó kockázati mérték kiválasztása még csak félsiker. A kockázat pontos méréséhez megbízható adatokra és becslési módszerekre van szükség. A pénzügyi folyamatok komplexitása miatt általában ezek egyike sem teljesül.
11 Hogyan kezeljük a kockázatot? A kockázatkezelés néhány technikája: Diverzifikáció Fedezeti ügyletek (hedge-elés) Kereskedési limitrendszer Biztosítékok Tőkemegfelelés Rendszerbiztonság
12 Miről lesz tehát szó? A portfólióválasztási probléma A kockázatmérés módjai és problémái A kockázatbecslés problémái
13 A portfólió fogalma A befektetők a pénzügyi piacokon számtalan termék közül választhatnak. Egy befektető tulajdonában lévő termékek összességét az adott befektető portfóliójának nevezzük. Jelölje a befektetési lehetőségek számát N. Ekkor a portfóliót egy N-dimenziós w vektor írja le. A vektor w i komponense az i. értékpapírba fektetett összeg. A w vektor komponenseit portfóliósúlyoknak nevezzük.
14 A Markowitz-modell A portfólió választás első matematikai modelljét a Nobel-díjas Harry Markowitz alkotta meg (1952). Modellfeltevések: A befektetések hozama normális eloszlású. Egy befektetés kockázatát hozamának szórásával mérjük. A rövidre eladás korlátlanul megengedett. (A portfólió súlyok negatívak is lehetnek.) Az egyes pénzügyi termékekből tetszőleges hányadot (pl db) vehetünk. A befektetők racionálisak, azonos információ alapján döntenek.
15 A hozamok eloszlása Jelöljünk ki egy T befektetési időtávot. (Pl. 1 hónap, 1 év stb.) Legyen az i. termék értéke t időpontban S i (t). Ennek a terméknek a hozama a T időszakban X i = S i (T ) S i (0). A hozamok legyenek Gauss-eloszlásúak µ i = E[X i ] várható értékekkel és σ ij = E[X i X j ] E[X i ]E[X j ] kovarianciákkal
16 A portfóliók kockázata Tekintsünk egy w portfóliót! A portfólió hozama: X (w) = i w ix i. A portfólió várható hozama: µ(w) = i w iµ i. A portfólió varianciája: σ 2 (w) = i,j σ ijw i w j. A portfólió kockázata, azaz szórása tehát σ(w).
17 Diverzifikáció A szórás w konvex függvénye, azaz i w i = 1 mellett ( ) σ w i X i w i σ (X i ). i i Ezért tehát jobban járunk, ha nem egy értékpapírba fektetünk, hanem több értékpapír kombinációjába. Ezt nevezzük diverzifikációnak. De miért előnyös a diverzifikáció?
18 A diverzifikációs hatás Tekintsünk két értékpapírt X és Y hozammal! Legyen X és Y szórása σ X és σ Y, korrelációjuk pedig ρ Készítsünk portfóliót w és 1 w súlyokkal! A portfólió hozamának varianciája: σ 2 (w) = w 2 σ 2 X + (1 w)2 σ 2 Y + 2w(1 w)ρσ X σ Y Vizsgáljuk meg, mi történik különböző korrelációk mellett!
19 Tökéletesen korrelált hozamok Ha ρ = 1, akkor σ(w) = wσ X + (1 w)σ Y. Tökéletes korreláció mellett a kockázatok összeadódnak. Ilyen esetben tehát nincs diverzifikációs előny.
20 Tökéletesen antikorrelált hozamok Ha ρ = 1, akkor σ(w) = wσ X (1 w)σ Y. Tökéletes korreláció mellett a kockázatok kivonódnak egymásból. Így a w/(1 w) = σ Y /σ X választás mellett az eredő variancia zérus. Ilyen esetben tehát a kockázat diverzifikációval teljesen megszüntethető.
21 Nem tökéletesen korrelált hozamok Ha 1 < ρ < 1, akkor wσ X (1 w)σ Y < σ(w) < wσ X + (1 w)σ Y. Az eredő kockázat tehát kisebb az egyedi kockázatok összegénél, de biztosan nagyobb, mint nulla. Ilyenkor a kockázat csökkenthető diverzifikációval, de el nem tüntethető. A diverzifikáció tehát úgy mérsékli a kockázatot, hogy a hozamok egyedi ingadozásait kiátlagolja. A legjobb diverzifikációs hatást biztosító portfólió megkeresését portfólió-optimalizációnak vagy portfólióválasztásnak nevezzük.
22 A Markowitz-féle portfólió-optimalizációs feladat Egységnyi indulótőkével µ nagyságú várható hozamot szeretnénk elérni a lehető legalacsonyabb kockázatot mellett: min w R N N i=1 j=1 N σ ij w i w j N w i µ i = µ i=1 N w i = 1 i=1
23 A portfóliók kockázata A feladatot a Lagrange-multiplikátorok módszerével megoldva: σ 2 (µ) = ( A AC B 2 µ B ) A A, ahol A = i,j σ 1 ij, B = i,j σ 1 ij µ j és C = i,j σ 1 ij µ i µ j. Ez a görbe minden µ-höz megadja az elérhető legalacsonyabb kockázatot. A µ hozamú és σ (µ) kockázatú portfóliókat hatékonynak nevezzük.
24 Lehetséges, határ- és hatékony portfóliók
25 A portfóliók kockázata Racionális befektető tehát csak hatékony portfóliót választ. Minél nagyobb várható hozamot szeretnénk elérni, annál nagyobb kockázatot kell vállalnunk. A hatékony portfóliók közötti választás a befektetők szubjektív döntése. Az agresszív befektetők szívesen vállalnak nagy kockázatot, a konzervatív befektetők azonban inkább beérik alacsonyabb hozammal. A preferenciákat az ún. utilitás (hasznosság) függvénnyel szokás leírni, ezzel azonban itt nem foglalkozunk.
26 A kockázatmentes eszköz Tegyük fel, hogy létezik kockázatmentes befektetés. Ennek tehát a szórása zérus, hozama legyen µ 0. Kockázatmentesnek általában az államkötvényeket, vagy a legtőkeerősebb bankok betéteit szokás tekinteni. Szigorúan véve persze kockázatmentes befektetés nem létezik, de nagyon hasznos absztrakció. Egészítsük ki portfólió-modellünket a kockázatos termékkel!
27 Hatékony portfóliók kockázatmentes eszköz mellett
28 Hatékony portfóliók kockázatmentes eszköz mellett A csak kockázatmentes eszközt tartalmazó portfóliónak a (0, µ 0 ) pont felel meg. Ezt az eszközt szabadon kombinálhatjuk bármilyen kockázatos portfólióval. A lehetséges portfóliók tehát a (0, µ 0 ) pontból kiinduló egyenesek lesznek. A hatékony portfóliók halmaza kockázatos portfóliók paraboláját felülről érintő egyenes. Ezt tőkepiaci egyenesnek nevezzük. (Capital Market Line, CML) Az értintési pontbeli portfólió neve piaci portfólió, kockázata σ M, várható hozama µ M.
29 Hatékony portfóliók kockázatmentes eszköz mellett Ha van kockázatmentes eszköz, akkor minden befektető a CML-en helyezkedik el, ahol µ = µ 0 + µ M µ 0 σ σ M Minden portfólió w 0 egység kockázatmentes eszközből és 1 w 0 egység piaci portfólióból áll. Ha w 0 > 0, akkor kölcsönadunk µ 0 kamatra w 0 -t a többit pedig a piaci portfólióba fektetjük. Ha w 0 = 0, akkor minden pénzünket a piaci portfólióba fektetjük. Ha w 0 < 0, akkor kölcsönveszünk µ 0 kamatra w 0 -t és meglévő pénzünk mellett azt is a piaci portfólióba fektetjük.
30 A Markowitz modell fő tanulságai A diverzifikáció csökkenti a kockázatot. Racionális befektetők a hatékony portfóliók közül válogatnak. Nagyobb várható hozamért cserébe nagyobb kockázatot kell vállalnunk. Ha van kockázatmentes eszköz, akkor a kockázatos eszközöknek mindenki ugyanazt a kombinációját tartja.
31 A Markowitz modell korlátai A normalitás általában nem teljesül. Statikus szemléletű. (Stacionárius folyamat, egyetlen befektetési periódus) A szórás csak szimmetrikus, véges varianciájú eloszlásokra elfogadható kockázati mérték. Csak egyensúlyt modellez. Rövidre eladási, likviditási, stb. korlátok figyelmen kívül hagyása. Információs aszimmetriák. Becslési hibák kérdése. Stb.
32 Kockázati mértékek
33 A szórás előnyei Szemléletes jelentésű, a jövőbeli megtérülés bizonytalanságát méri. Az eredő kockázat több, akár nagyon eltérő jellegű befektetésre is meghatározható. Konvex, tehát a diverzifikáció hatására csökken. A portfóliósúlyoknak jól kezelhető (pl. differenciálható) függvénye.
34 A szórás hátrányai Nem minden eloszlásra létezik. (Pl. 2-nél kisebb kitevőjű, hatványfarkú eloszlásokra nem.) Az eloszlás szélére nem elég érzékeny. Nem tesz különbséget nyereség és veszteség között. (A váratlanul nagy nyereségtől nem félünk, csak a váratlanul nagy veszteségtől.)
35 Átlagos abszolút eltérés Egy X hozamú befektetés átlagos abszolút eltérése (Mean Absolute Deviation, MAD): MAD(X ) = E X EX Hasonlít a szórásra. Előnye: érzékenyebb a szélekre, mint a szórás; 1-nél nagyobb kitevőjű, hatványfarkú eloszlásra is létezik, konvex Hátránya: a portfólió súlyok nemdifferenciálható függvénye
36 Szemivariancia Egy X hozamú befektetés szemivarianciája: ν 2 (X ) = E (min{0, X EX }) 2 Ez a varianciától abban tér el, hogy csak az átlag alatti eltérések négyzetének a várható értékét vesszük. Előnye: csak az átlag alatti hozamokat veszi figyelembe, konvex Hátránya: pontosan akkor létezik, amikor a szórás; az eloszlás szélére nem elég érzékeny, a portfólió súlyok nemdifferenciálható függvénye
37 Kockázatott érték A kockáztatott érték (Value-at-Risk, VaR) a 80-as évek óta az egyik legnépszerűbb kockázati mérték. Azt mondjuk, egy befektetés VaR-ja α konfidenciaszinten az a pénzösszeg, amelynél többet csak 1 α valószínűséggel veszíthetünk. Más lehetséges megfogalmazások: Az 1 α százaléknyi legrosszabb eset közül a legjobb esetben elszenvedett veszteség. Az α százaléknyi legjobb eset közül a legrosszabb esetben elszenvedett veszteség. Az α tipikus értékei: 95%, 99%. A VaR tehát a hozameloszlás kvantilise.
38 VaR folytonos eloszlásokra Tegyük fel, hogy egy befektetés hozama X, melynek eloszlásfüggvénye F (x) invertálható, például mert folytonos. Ekkor VaR(X ) = F 1 (1 α). A mínusz előjel azért kell, mert a veszteségekhez pozitív kockázatot rendelünk. A VaR tehát az az érték, amelynél kisebb értékekre a valószínűségsűrűség-függvény alatti terület éppen 1 α: 1 α = VaR(X ) f (x)dx.
39 VaR folytonos sűrűségfüggvény mellett
40 VaR diszkrét eloszlásokra Diszkrét eloszlások esetén az F (X ) eloszlásfüggvény lépcsős, nem invertálható. Pl.: X 5%-5%-90% eséllyel 500Ft, 100Ft és 1000Ft. Ekkor a VaR vajon 500Ft vagy 100Ft? Az előbbit alsó VaR-nak (VaR 5% (X )), az utóbbit felső VaR-nak (VaR 5% (X )) nevezzük. Általánosan: VaR α (X ) = sup{x F (x) < α}, VaR α (X ) = inf{x F (x) > α}. Triviálisan VaR α (X ) VaR α (X ). Ha F (x) folytonos, akkor VaR α (X ) = VaR α (X ).
41 VaR diszkrét sűrűségfüggvény mellett
42 A VaR előnyei Kifejezetten a veszteségekre koncentrál. Tetszőleges eloszlásra létezik. Az eredő kockázat tetszőleges jellegű befektetések kombinációjára meghatározható. A kockázatot pénzveszteségben fejezi ki.
43 A VaR hátrányai A portfóliósúlyok nemdifferenciálható függvénye. Nem konvex. A VaR-nál nagyobb veszteségek eloszlása nem számít. Az utóbbi két hiányosság igen súlyos.
44 A VaR normális eloszlás mellett Legyen X eloszlása normális µ és σ paraméterekkel. Ekkor belátható, hogy VaR α (X ) = σφ 1 (1 α) µ, ahol Φ(x) a standard normális eloszlásfüggvény. Ilyenkor a VaR konvex lesz. A VaR-nál nagyobb veszteségekről azonban a VaR továbbra sem mond semmit.
45 A koherens kockázati mértékek Hátrányai miatt a VaR általában alkalmatlan a kockázat mérésére. Ennek ellenére a gyakorlatban és a szabályozásban széleskörűen alkalmazzák. Ennek oka többek között a rendszer tehetetlensége. A koherens kockázati mértékek fogalma többek között a VaR (és egyéb mértékek) problémáira próbál választ adni. Hivatkozás: P Artzner, F Delbaen, JM Eber, D Heath, Coherent Measures of Risk, Mathematical Finance Vol. 9, Num. 3. (1999)
46 A koherens kockázati mértékek definíciója Legyen Ω a hozamokat reprezentáló val. változók halmaza. Egy ρ : Ω R függvényt kockázati mértéknek nevezünk. Egy ρ kockázati mérték koherens, ha teljesíti az alábbi négy feltételt: Monotonitás: X, Y Ω, X Y ρ(x ) ρ(y ) Szubadditivitás: X, Y Ω, ρ(x + Y ) ρ(x ) + ρ(y ) Pozitív homogenitás: X Ω, a > 0 ρ(ax ) = aρ(x ) Transzláció invariancia: X Ω, a R ρ(x + a) = ρ(x ) a A fenti tulajdonságokat koherencia axiómáknak is nevezik.
47 Az axiómák szavakban Monotonitás: Ha A befektetés hozama sohasem kisebb, mint B-jé, akkor A nem lehet kockázatosabb B-nél. Szubadditivitás: A és B befektetések eredő kockázata nem lehet nagyobb, mint egyedi kockázataik összege. Pozitív homogenitás: Ha egy értékpapírba kétszer vagy háromszor annyi pénzt fektetünk, a kockázat is kétszer, háromszor akkora lesz. Transzláció invariancia: Ha pozíciónkhoz a hozamú kockázatmentes eszközt adunk, akkor a kockázatunk a-val csökken.
48 Megjegyzések a koherencia axiómákról A szubadditivitásból és a pozitív homogenitásból következik a konvexitás. Ez fordítva nem igaz! A szubadditivitás és pozitív homogenitás érvényessége vitatható. (Nagy pozíciókra, vagy alacsony likviditás mellett pl. nem érvényes.) A konvexitást azonban mindig elvárjuk. A transzláció invariancia miatt a koherens mértékek a kockázatot pénzveszteségben mérik. Emiatt a koherens mértékek elvileg jól alkalmazhatók a tőkemegfelelési szabályozásban. A VaR nem szubadditív, a szórás és MAD nem transzlációinvariáns.
49 A feltételes VaR (CVaR) A VaR egyik hibája (a konvexitás hiánya mellett), hogy a legnagyobb veszteségeket figyelmen kívül hagyja. Ezt orvosolja az (alsó és felső) Feltételes VaR: CVaR α (X ) = E [X X < VaR α (X )] CVaR α (X ) = E [X X VaR α (X )] A CVaR tehát az 1 α százaléknyi legrosszabb kimenetel átlaga. Belátható, hogy a VaR-hoz hasonlóan a CVaR általában nem szubadditív, tehát nem is koherens. (A többi három axiómát teljesíti.)
50 Az Expected Shortfal (ES) Egy apró változtatással a CVaR koherenssé tehető. Ehhez az átlagolás küszöbét nem veszteségben, hanem valószínűségben kell megadni. Az így kapott kockázati mérték az Expected Shortfall: ES α (X ) = 1 1 α 1 α VaR p (X )dp,
51 Az ES folytonos eloszlásokra Tegyük fel, hogy F X (x) differenciálható (tehát invertálható). Ekkor VaR α = F 1 (1 α). X Ilyenkor tehát az ES: ES α (X ) = 1 1 α = 1 1 α 0 VaRα(X ) 1 α F 1 X (p)dp = f X (x)xdx = E [X X VaR α (X )]. Azaz CVaR α (X ) = CVaR α (X ) = ES α (X ).
52 Az ES folytonos eloszlásokra
53 Az ES diszkrét eloszlásokra Ekkor F X (x) nem invertálható. Előfordulhat, hogy VaR α (X ) > VaR α (X ). Például legyen X % valószínűséggel -600Ft, -60Ft és 800Ft. Ekkor CVaR 95% = 600Ft, CVaR 95% = Ft Ft = 420Ft. Az ES azonban a 2% valószínűségű 60Ft-os veszteséget csak 1% erejéig veszi figyelembe: ES 95% = Ft Ft = 492Ft. Általában is igaz, hogy CVaR α (X ) ES α (X ) CVaR α (X ).
54 Az ES diszkrét eloszlásokra
55 Az ES előnyei Belátható, hogy az ES koherens mérték. Az ES tehát konvex. Figyelembe veszi a legnagyobb lehetséges veszteségeket. Bár a portfólió súlyok nemdifferenciálható függvénye, a portfólióválasztási feladat egy könnyen kezelhető lineáris programozási problémára vezet. (Az ES-nek hátrányai is vannak, erre később még röviden visszatérünk.)
56 A kockázat becslése Eddig feltettük, hogy a hozamok eloszlását és annak paramétereit ismerjük. A gyakorlatban természetesen nem ez a helyzet. Gyakran még megközelítőleg sincs fogalmunk az árfolyamokat vezérlő folyamatokról. Ilyenkor múltbeli (historikus) megfigyelésekre kell hagyatkoznunk. Portfóliót tehát csak bizonyos (nem feltétlenül helyes) előfeltevések, és véges számú megfigyelés alapján tudunk választani.
57 A Markowitz-modell véges minta mellett Az egyszerűség kedvéért tegyük fel, hogy a hozamok eloszlása továbbra is normális. Az eloszlás paramétereit ugyanakkor nem ismerjük, tehát becsülnünk kell. Tegyük fel, hogy az N db. értékpapír hozamát megfigyeltük T db. egymást követő időszakban. Az i. értékpapír realizált hozama a t. időszakban legyen x it. Az x it megfigyelések tehát egy N T -s mátrixba írhatók.
58 Hatékony portfóliók becslése Az értékpapírok becsült hozamai és kovariancia mátrixa: ˆµ i = 1 T T t=1 ˆσ ij = 1 T 1 x it T (x it ˆµ i )(x jt ˆµ j ) t=1 Egy w portfólió becsült kockázata ˆσ 2 (w) = ij ˆσ ijw i w j. A hatékony portfóliók becsléséhez tehát ˆσ 2 (w)-t kell minimalizálnunk, i w i ˆµ i = µ és i w i = 1 mellett.
59 A becslési hiba jellemzése Tegyük most fel, hogy ismerjük a hozamok eloszlásának valódi µ i, σ ij paramétereit. A valódi optimális portfólió: wi. Ennek kockázata: ij σ ijwi w j. Képzeljük magunkat a befektető helyébe, aki csak ˆµ i -t és ˆσ ij -t ismeri. A becsült optimális portfólió: ŵi. A becsült optimum VALÓDI kockázata: ij σ ijŵi ŵ j. Vezessük be a következő mennyiséget: q 0 = ij σ ijŵi ŵ j ij σ ijwi w j
60 A becslési hiba jellemzése q 0 = ij σ ijŵi ŵ j ij σ ijwi w j Tehát q 0 1, és q 0 1 megmondja, hány százalékkal vállal a befektető nagyobb kockázatot amiatt, hogy az eloszlás paramétereit csak mintából tudja becsülni. A befektető q 0 -t természetesen nem tudja kiszámolni, de ha mi generáljuk a folyamatot, akkor mi igen. A becsült optimum, így q 0 is mintáról mintára ingadozik.
61 A becslési hiba jellemzése q 0 tehát véletlen változó, de numerikus vagy analitikus módszerrel tanulmányozhatjuk eloszlását és momentumait. Ebben felhasználható például a részecskefizikában alkalmazott véletlenmátrix-elmélet, vagy a spinüvegek modellezésében alkalmazott replika-módszer. q 0 fő tulajdonságai: q 0 szórása az N limeszben 0-hoz tart. 1 Az N és N/T = const limeszben q 0 = 1 N/T Véges N-re és T -re E[q0 2] 1 1 N/T Az N N/T = const limeszben tehát q 0 egyáltalán nem függ µ i -től és σ ij -től!
62 A becslési hiba jellemzése Azt látjuk tehát, hogy amint T N, a becslési hiba divergál! Ha például T = 2N, akkor q 0 2 = , tehát ha kétszer annyi megfigyelésünk van, mint értékpapírunk, akkor a becsült optimum kockázata átlagosan 41%-kal lesz magasabb, mint a valódi optimumé. Ha T < N, akkor nincs megoldás. Ez annak a következménye, hogy ilyenkor ˆσ ij nem invertálható. A valóságban persze az eloszlások nem normálisak, sőt nem is stacionáriusak, így az amúgy is divergens q 0 minden bizonnyal még alul is becsüli a becslési hibát.
63 További megjegyzések A kovariancia mátrix becslése számos módon javítható. A fenti analízis más kockázati mértékekre is elvégezhető. Különösen érdekes eredményt kapunk az ES-re: a becsült ES-nek nem minden mintán van minimuma, így az ES becslése a szórásénál is sokkal instabilabb! Ez ráadásul minden koherens mértékre igaz, ami komolyan megkérdőjelezi gyakorlati alkalmazhatóságukat.
64 Néhány érdekes téma A tőkemegfelelési szabályok, és az általuk definiált kockázati mértékek A kockázat becslési módszerei Dinamikus kockázati mértékek Hitelkockázat és működési kockázat...
Diverzifikáció Markowitz-modell MAD modell CAPM modell 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Kockázatos pénzügyi eszközök
 Kockázatos pénzügyi eszközök Tulassay Zsolt zsolt.tulassay@uni-corvinus.hu Tőkepiaci és vállalati pénzügyek 2006. tavasz Budapesti Corvinus Egyetem 2006. március 1. Motiváció Mi a fő különbség (pénzügyi
Kockázatos pénzügyi eszközök Tulassay Zsolt zsolt.tulassay@uni-corvinus.hu Tőkepiaci és vállalati pénzügyek 2006. tavasz Budapesti Corvinus Egyetem 2006. március 1. Motiváció Mi a fő különbség (pénzügyi
Kockázati Mértékek Instabilitása
 Kockázati Mértékek Instabilitása Doktori értekezés Varga-Haszonits István Témavezető: Dr. Kondor Imre DSc, egyetemi tanár ELTE TTK Komplex Rendszerek Fizikája Tanszék ELTE TTK Fizika Doktori Iskola Iskolavezető:
Kockázati Mértékek Instabilitása Doktori értekezés Varga-Haszonits István Témavezető: Dr. Kondor Imre DSc, egyetemi tanár ELTE TTK Komplex Rendszerek Fizikája Tanszék ELTE TTK Fizika Doktori Iskola Iskolavezető:
A Markowitz modell: kvadratikus programozás
 A Markowitz modell: kvadratikus programozás Harry Markowitz 1990-ben kapott Közgazdasági Nobel díjat a portfolió optimalizálási modelljéért. Ld. http://en.wikipedia.org/wiki/harry_markowitz Ennek a legegyszer
A Markowitz modell: kvadratikus programozás Harry Markowitz 1990-ben kapott Közgazdasági Nobel díjat a portfolió optimalizálási modelljéért. Ld. http://en.wikipedia.org/wiki/harry_markowitz Ennek a legegyszer
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
A portfólió elmélet általánosításai és következményei
 A portfólió elmélet általánosításai és következményei Általánosan: n kockázatos eszköz allokációja HOZAM: KOCKÁZAT: variancia-kovariancia mátrix segítségével! ) ( ) ( ) / ( ) ( 1 1 1 n s s s p t t t s
A portfólió elmélet általánosításai és következményei Általánosan: n kockázatos eszköz allokációja HOZAM: KOCKÁZAT: variancia-kovariancia mátrix segítségével! ) ( ) ( ) / ( ) ( 1 1 1 n s s s p t t t s
A Markowitz modell: kvadratikus programozás
 A Markowitz modell: kvadratikus programozás Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2011/12 tanév, II. félév Losonczi László (DE) A Markowitz modell 2011/12 tanév,
A Markowitz modell: kvadratikus programozás Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2011/12 tanév, II. félév Losonczi László (DE) A Markowitz modell 2011/12 tanév,
Valószínűségi változók. Várható érték és szórás
 Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
A maximum likelihood becslésről
 A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
Gazdasági matematika II. vizsgadolgozat, megoldással,
 Gazdasági matematika II. vizsgadolgozat, megoldással, levelező képzés Definiálja az alábbi fogalmakat! 1. Kvadratikus mátrix invertálhatósága és inverze. (4 pont) Egy A kvadratikus mátrixot invertálhatónak
Gazdasági matematika II. vizsgadolgozat, megoldással, levelező képzés Definiálja az alábbi fogalmakat! 1. Kvadratikus mátrix invertálhatósága és inverze. (4 pont) Egy A kvadratikus mátrixot invertálhatónak
(Independence, dependence, random variables)
 Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
5. elıadás március 22. Portfólió-optimalizálás
 5. elıadás 203. március 22. Portfólió-optimalizálás Alapfeladat Cél: minél nagyobb várható hozam elérése De: közben a kockázat legyen minél kisebb Kompromisszum: elvárt hozamot érje el a várható érték
5. elıadás 203. március 22. Portfólió-optimalizálás Alapfeladat Cél: minél nagyobb várható hozam elérése De: közben a kockázat legyen minél kisebb Kompromisszum: elvárt hozamot érje el a várható érték
A L Hospital-szabály, elaszticitás, monotonitás, konvexitás
 A L Hospital-szabály, elaszticitás, monotonitás, konvexitás 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék A L Hospital-szabály, elaszticitás, monotonitás, konvexitás p. / A L
A L Hospital-szabály, elaszticitás, monotonitás, konvexitás 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék A L Hospital-szabály, elaszticitás, monotonitás, konvexitás p. / A L
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Statisztikai következtetések Nemlineáris regresszió Feladatok Vége
 [GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
[GVMGS11MNC] Gazdaságstatisztika 10. előadás: 9. Regressziószámítás II. Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet A standard lineáris modell
Nagy számok törvényei Statisztikai mintavétel Várható érték becslése. Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem
 agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
Kockázati Mértékek Instabilitása
 Kockázati Mértékek Instabilitása Doktori értekezés tézisei Varga-Haszonits István ELTE TTK Fizika Doktori Iskola Statisztikus fizika, biológiai fizika és kvantumrendszerek fizikája program Iskolavezető:
Kockázati Mértékek Instabilitása Doktori értekezés tézisei Varga-Haszonits István ELTE TTK Fizika Doktori Iskola Statisztikus fizika, biológiai fizika és kvantumrendszerek fizikája program Iskolavezető:
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Az eszközalap tervezett befektetési korlátai: Eszközcsoport Minimális arány Maximális arány Megcélzott arány. Mögöttes befektetési alap 90% 100% 100%
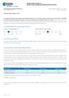 AEGON TEMPÓ ALLEGRO 10 Az eszközalap kizárólag az Aegon Magyarország Befektetési Alapkezelő Zrt. által kezelt, forintban denominált Aegon Tempó Allegro 10 Alapokba Aegon Tempó Allegro 10 Alapok Alapja
AEGON TEMPÓ ALLEGRO 10 Az eszközalap kizárólag az Aegon Magyarország Befektetési Alapkezelő Zrt. által kezelt, forintban denominált Aegon Tempó Allegro 10 Alapokba Aegon Tempó Allegro 10 Alapok Alapja
Elméleti összefoglaló a Valószín ségszámítás kurzushoz
 Elméleti összefoglaló a Valószín ségszámítás kurzushoz Véletlen kísérletek, események valószín sége Deníció. Egy véletlen kísérlet lehetséges eredményeit kimeneteleknek nevezzük. A kísérlet kimeneteleinek
Elméleti összefoglaló a Valószín ségszámítás kurzushoz Véletlen kísérletek, események valószín sége Deníció. Egy véletlen kísérlet lehetséges eredményeit kimeneteleknek nevezzük. A kísérlet kimeneteleinek
Társaságok pénzügyei kollokvium
 udapesti Gazdasági Főiskola Pénzügyi és Számviteli Főiskolai Kar udapesti Intézet Továbbképzési Osztály Társaságok pénzügyei kollokvium Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 55 60 pont
udapesti Gazdasági Főiskola Pénzügyi és Számviteli Főiskolai Kar udapesti Intézet Továbbképzési Osztály Társaságok pénzügyei kollokvium Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 55 60 pont
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 9. Együttes eloszlás, kovarianca, nevezetes eloszlások Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés, definíciók Együttes eloszlás Függetlenség
BIOMATEMATIKA ELŐADÁS 9. Együttes eloszlás, kovarianca, nevezetes eloszlások Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés, definíciók Együttes eloszlás Függetlenség
Biometria az orvosi gyakorlatban. Korrelációszámítás, regresszió
 SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
A kockázat fogalma. A kockázat fogalma. Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András
 Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András A kockázat fogalma A kockázat (def:) annak kifejezése, hogy valami nem kívánt hatással lesz a valaki/k értékeire, célkitűzésekre. A kockázat
Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András A kockázat fogalma A kockázat (def:) annak kifejezése, hogy valami nem kívánt hatással lesz a valaki/k értékeire, célkitűzésekre. A kockázat
STATISZTIKA. A maradék független a kezelés és blokk hatástól. Maradékok leíró statisztikája. 4. A modell érvényességének ellenőrzése
 4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
Gazdasági matematika II. vizsgadolgozat megoldása A csoport
 Gazdasági matematika II. vizsgadolgozat megoldása A csoport Definiálja az alábbi fogalmakat!. Egy eseménynek egy másik eseményre vonatkozó feltételes valószínűsége. ( pont) Az A esemény feltételes valószínűsége
Gazdasági matematika II. vizsgadolgozat megoldása A csoport Definiálja az alábbi fogalmakat!. Egy eseménynek egy másik eseményre vonatkozó feltételes valószínűsége. ( pont) Az A esemény feltételes valószínűsége
Statisztika I. 4. előadás Mintavétel. Kóczy Á. László KGK-VMI. Minta Mintavétel Feladatok. http://uni-obuda.hu/users/koczyl/statisztika1.
 Statisztika I. 4. előadás Mintavétel http://uni-obuda.hu/users/koczyl/statisztika1.htm Kóczy Á. László KGK-VMI koczy.laszlo@kgk.uni-obuda.hu Sokaság és minta Alap- és mintasokaság A mintasokaság az a részsokaság,
Statisztika I. 4. előadás Mintavétel http://uni-obuda.hu/users/koczyl/statisztika1.htm Kóczy Á. László KGK-VMI koczy.laszlo@kgk.uni-obuda.hu Sokaság és minta Alap- és mintasokaság A mintasokaság az a részsokaság,
Statisztika I. 4. előadás Mintavétel. Kóczy Á. László KGK-VMI. Minta Mintavétel Feladatok. http://uni-obuda.hu/users/koczyl/statisztika1.
 Statisztika I. 4. előadás Mintavétel http://uni-obuda.hu/users/koczyl/statisztika1.htm Kóczy Á. László KGK-VMI koczy.laszlo@kgk.uni-obuda.hu Sokaság és minta Alap- és mintasokaság A mintasokaság az a részsokaság,
Statisztika I. 4. előadás Mintavétel http://uni-obuda.hu/users/koczyl/statisztika1.htm Kóczy Á. László KGK-VMI koczy.laszlo@kgk.uni-obuda.hu Sokaság és minta Alap- és mintasokaság A mintasokaság az a részsokaság,
e (t µ) 2 f (t) = 1 F (t) = 1 Normális eloszlás negyedik centrális momentuma:
 Normális eloszlás ξ valószínűségi változó normális eloszlású. ξ N ( µ, σ 2) Paraméterei: µ: várható érték, σ 2 : szórásnégyzet (µ tetszőleges, σ 2 tetszőleges pozitív valós szám) Normális eloszlás sűrűségfüggvénye:
Normális eloszlás ξ valószínűségi változó normális eloszlású. ξ N ( µ, σ 2) Paraméterei: µ: várható érték, σ 2 : szórásnégyzet (µ tetszőleges, σ 2 tetszőleges pozitív valós szám) Normális eloszlás sűrűségfüggvénye:
Kockázati modellek (VaR és cvar)
 Kockázati modellek (VaR és cvar) BSc Szakdolgozat Írta: Kutas Éva Matematika BSc Alkalmazott matematikus szakirány Témavezet Mádi-Nagy Gergely egyetemi adjunktus Operációkutatási Tanszék Eötvös Loránd
Kockázati modellek (VaR és cvar) BSc Szakdolgozat Írta: Kutas Éva Matematika BSc Alkalmazott matematikus szakirány Témavezet Mádi-Nagy Gergely egyetemi adjunktus Operációkutatási Tanszék Eötvös Loránd
x, x R, x rögzített esetén esemény. : ( ) x Valószínűségi Változó: Feltételes valószínűség: Teljes valószínűség Tétele: Bayes Tétel:
 Feltételes valószínűség: Teljes valószínűség Tétele: Bayes Tétel: Valószínűségi változó általános fogalma: A : R leképezést valószínűségi változónak nevezzük, ha : ( ) x, x R, x rögzített esetén esemény.
Feltételes valószínűség: Teljes valószínűség Tétele: Bayes Tétel: Valószínűségi változó általános fogalma: A : R leképezést valószínűségi változónak nevezzük, ha : ( ) x, x R, x rögzített esetén esemény.
Készítette: Fegyverneki Sándor
 VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
Biztosítók kockázatdiverzifikációja
 Közgazdasági Szemle, LVII. évf., 00. július augusztus (634 65. o.) SZÜLE BORBÁLA Biztosítók kockázatdiverzifikációja A biztosítók működését általában több homogén részállományból összetevődő heterogén
Közgazdasági Szemle, LVII. évf., 00. július augusztus (634 65. o.) SZÜLE BORBÁLA Biztosítók kockázatdiverzifikációja A biztosítók működését általában több homogén részállományból összetevődő heterogén
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév
 Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév 1. A várható érték és a szórás transzformációja 1. Ha egy valószínűségi változóhoz hozzáadunk ötöt, mínusz ötöt, egy b konstanst,
Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév 1. A várható érték és a szórás transzformációja 1. Ha egy valószínűségi változóhoz hozzáadunk ötöt, mínusz ötöt, egy b konstanst,
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Normák, kondíciószám
 Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Társaságok pénzügyei kollokvium
 udapesti Gazdasági Főiskola Pénzügyi és Számviteli Főiskolai Kar udapesti Intézet Továbbképzési Osztály Társaságok pénzügyei kollokvium F Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 55 60 pont
udapesti Gazdasági Főiskola Pénzügyi és Számviteli Főiskolai Kar udapesti Intézet Továbbképzési Osztály Társaságok pénzügyei kollokvium F Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 55 60 pont
CHT& NSZT Hoeffding NET mom. stabilis. 2011. november 9.
 CHT& NSZT Hoeffding NET mom. stabilis Becslések, határeloszlás tételek Székely Balázs 2011. november 9. CHT& NSZT Hoeffding NET mom. stabilis 1 CHT és NSZT 2 Hoeffding-egyenlőtlenség Alkalmazása: Beengedés
CHT& NSZT Hoeffding NET mom. stabilis Becslések, határeloszlás tételek Székely Balázs 2011. november 9. CHT& NSZT Hoeffding NET mom. stabilis 1 CHT és NSZT 2 Hoeffding-egyenlőtlenség Alkalmazása: Beengedés
A lineáris programozás alapjai
 A lineáris programozás alapjai A konvex analízis alapjai: konvexitás, konvex kombináció, hipersíkok, félterek, extrém pontok, Poliéderek, a Minkowski-Weyl tétel (a poliéderek reprezentációs tétele) Lineáris
A lineáris programozás alapjai A konvex analízis alapjai: konvexitás, konvex kombináció, hipersíkok, félterek, extrém pontok, Poliéderek, a Minkowski-Weyl tétel (a poliéderek reprezentációs tétele) Lineáris
Principal Component Analysis
 Principal Component Analysis Principal Component Analysis Principal Component Analysis Definíció Ortogonális transzformáció, amely az adatokat egy új koordinátarendszerbe transzformálja úgy, hogy a koordináták
Principal Component Analysis Principal Component Analysis Principal Component Analysis Definíció Ortogonális transzformáció, amely az adatokat egy új koordinátarendszerbe transzformálja úgy, hogy a koordináták
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Hipotézis STATISZTIKA. Kétmintás hipotézisek. Munkahipotézis (H a ) Tematika. Tudományos hipotézis. 1. Előadás. Hipotézisvizsgálatok
 STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
Mikroökonómia II. B. ELTE TáTK Közgazdaságtudományi Tanszék. 8. hét AZ INFORMÁCIÓ ÉS KOCKÁZAT KÖZGAZDASÁGTANA, 1. rész
 MIKROÖKONÓMIA II. B ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia II. B AZ INFORMÁCIÓ ÉS KOCKÁZAT KÖZGAZDASÁGTANA, 1. rész Készítette: Szakmai felel s: 2011. február A tananyagot készítette: Jack
MIKROÖKONÓMIA II. B ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia II. B AZ INFORMÁCIÓ ÉS KOCKÁZAT KÖZGAZDASÁGTANA, 1. rész Készítette: Szakmai felel s: 2011. február A tananyagot készítette: Jack
Gazdasági matematika II. vizsgadolgozat megoldása, június 10
 Gazdasági matematika II. vizsgadolgozat megoldása, 204. június 0 A dolgozatírásnál íróeszközön kívül más segédeszköz nem használható. A dolgozat időtartama: 90 perc. Ha a dolgozat első részéből szerzett
Gazdasági matematika II. vizsgadolgozat megoldása, 204. június 0 A dolgozatírásnál íróeszközön kívül más segédeszköz nem használható. A dolgozat időtartama: 90 perc. Ha a dolgozat első részéből szerzett
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/47/23623719.jpg) [Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
[Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Bankismeretek 9. előadás. Lamanda Gabriella április 20.
 Bankismeretek 9. előadás Lamanda Gabriella lamanda@finance.bme.hu 2015. április 20. Miről volt szó? Aktív bankműveletek Hitelnyújtás Devizahitelezés problémaköre Lízing, faktoring Miről lesz szó? Banki
Bankismeretek 9. előadás Lamanda Gabriella lamanda@finance.bme.hu 2015. április 20. Miről volt szó? Aktív bankműveletek Hitelnyújtás Devizahitelezés problémaköre Lízing, faktoring Miről lesz szó? Banki
Biomatematika 2 Orvosi biometria
 Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Analízis II. Analízis II. Beugrók. Készítette: Szánthó József. kiezafiu kukac gmail.com. 2009/ félév
 Analízis II. Analízis II. Beugrók Készítette: Szánthó József kiezafiu kukac gmail.com 2009/20 10 1.félév Analízis II. Beugrók Függvények folytonossága: 1. Mikor nevez egy függvényt egyenletesen folytonosnak?
Analízis II. Analízis II. Beugrók Készítette: Szánthó József kiezafiu kukac gmail.com 2009/20 10 1.félév Analízis II. Beugrók Függvények folytonossága: 1. Mikor nevez egy függvényt egyenletesen folytonosnak?
Mi az adat? Az adat elemi ismeret. Az adatokból információkat
 Mi az adat? Az adat elemi ismeret. Tények, fogalmak olyan megjelenési formája, amely alkalmas emberi eszközökkel történő értelmezésre, feldolgozásra, továbbításra. Az adatokból gondolkodás vagy gépi feldolgozás
Mi az adat? Az adat elemi ismeret. Tények, fogalmak olyan megjelenési formája, amely alkalmas emberi eszközökkel történő értelmezésre, feldolgozásra, továbbításra. Az adatokból gondolkodás vagy gépi feldolgozás
biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás
 Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Matematika A3 Valószínűségszámítás, 5. gyakorlat 2013/14. tavaszi félév
 Matematika A3 Valószínűségszámítás, 5. gyakorlat 013/14. tavaszi félév 1. Folytonos eloszlások Eloszlásfüggvény és sűrűségfüggvény Egy valószínűségi változó, illetve egy eloszlás eloszlásfüggvényének egy
Matematika A3 Valószínűségszámítás, 5. gyakorlat 013/14. tavaszi félév 1. Folytonos eloszlások Eloszlásfüggvény és sűrűségfüggvény Egy valószínűségi változó, illetve egy eloszlás eloszlásfüggvényének egy
Exponenciális kisimítás. Üzleti tervezés statisztikai alapjai
 Exponenciális kisimítás Üzleti tervezés statisztikai alapjai Múlt-Jelen-Jövő kapcsolat Egyensúlyi helyzet Teljes konfliktus Részleges konfliktus: 0 < α < 1, folytatódik a múlt, de nem változatlanul módosítás:
Exponenciális kisimítás Üzleti tervezés statisztikai alapjai Múlt-Jelen-Jövő kapcsolat Egyensúlyi helyzet Teljes konfliktus Részleges konfliktus: 0 < α < 1, folytatódik a múlt, de nem változatlanul módosítás:
A vállalati pénzügyi döntések fajtái
 A vállalati pénzügyi döntések fajtái Hosszú távú finanszírozási döntések Befektetett eszközök Forgóeszközök Törzsrészvények Elsőbbségi részvények Hosszú lejáratú kötelezettségek Rövid lejáratú kötelezettségek
A vállalati pénzügyi döntések fajtái Hosszú távú finanszírozási döntések Befektetett eszközök Forgóeszközök Törzsrészvények Elsőbbségi részvények Hosszú lejáratú kötelezettségek Rövid lejáratú kötelezettségek
Mátrixjátékok tiszta nyeregponttal
 1 Mátrixjátékok tiszta nyeregponttal 1. Példa. Két játékos Aladár és Bendegúz rendelkeznek egy-egy tetraéderrel, melyek lapjaira rendre az 1, 2, 3, 4 számokat írták. Egy megadott jelre egyszerre felmutatják
1 Mátrixjátékok tiszta nyeregponttal 1. Példa. Két játékos Aladár és Bendegúz rendelkeznek egy-egy tetraéderrel, melyek lapjaira rendre az 1, 2, 3, 4 számokat írták. Egy megadott jelre egyszerre felmutatják
Analízis I. beugró vizsgakérdések
 Analízis I. beugró vizsgakérdések Programtervező Informatikus szak 2008-2009. 2. félév Készítette: Szabó Zoltán SZZNACI.ELTE zotyo@bolyaimk.hu v1.7 Forrás: Dr. Weisz Ferenc: Prog. Mat. 2006-2007 definíciók
Analízis I. beugró vizsgakérdések Programtervező Informatikus szak 2008-2009. 2. félév Készítette: Szabó Zoltán SZZNACI.ELTE zotyo@bolyaimk.hu v1.7 Forrás: Dr. Weisz Ferenc: Prog. Mat. 2006-2007 definíciók
Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére
 Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére Zubor Zoltán MNB - Biztosításfelügyeleti főosztály MAT Tavaszi Szimpózium 2016. május 7. 1 Háttér Bit. 99. : folyamatos
Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére Zubor Zoltán MNB - Biztosításfelügyeleti főosztály MAT Tavaszi Szimpózium 2016. május 7. 1 Háttér Bit. 99. : folyamatos
VÁLLALATGAZDASÁGTAN II. Döntési Alapfogalmak
 Vállalkozási VÁLLALATGAZDASÁGTAN II. Tantárgyfelelős: Prof. Dr. Illés B. Csaba Előadó: Dr. Gyenge Balázs Az ökonómiai döntés fogalma Vállalat Környezet Döntések sorozata Jövő jövőre vonatkozik törekszik
Vállalkozási VÁLLALATGAZDASÁGTAN II. Tantárgyfelelős: Prof. Dr. Illés B. Csaba Előadó: Dr. Gyenge Balázs Az ökonómiai döntés fogalma Vállalat Környezet Döntések sorozata Jövő jövőre vonatkozik törekszik
Kockázati mértékek összehasonlítása. BSc Szakdolgozat
 Kockázati mértékek összehasonlítása BSc Szakdolgozat Írta: Kertész Mónika Matematika BSc, Alkalmazott matematikus szakirány Témavezető: Zempléni András egyetemi docens Valószínűségelméleti és Statisztika
Kockázati mértékek összehasonlítása BSc Szakdolgozat Írta: Kertész Mónika Matematika BSc, Alkalmazott matematikus szakirány Témavezető: Zempléni András egyetemi docens Valószínűségelméleti és Statisztika
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
Least Squares becslés
 Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit.
 2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
MIKROÖKONÓMIA II. B. Készítette: K hegyi Gergely. Szakmai felel s: K hegyi Gergely. 2011. február
 MIKROÖKONÓMIA II. B Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
MIKROÖKONÓMIA II. B Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
A valószínűségszámítás elemei
 A valószínűségszámítás elemei Kísérletsorozatban az esemény relatív gyakorisága: k/n, ahol k az esemény bekövetkezésének abszolút gyakorisága, n a kísérletek száma. Pl. Jelenség: kockadobás Megfigyelés:
A valószínűségszámítás elemei Kísérletsorozatban az esemény relatív gyakorisága: k/n, ahol k az esemény bekövetkezésének abszolút gyakorisága, n a kísérletek száma. Pl. Jelenség: kockadobás Megfigyelés:
Valószínűségszámítás összefoglaló
 Statisztikai módszerek BMEGEVGAT Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztikai módszerek BMEGEVGAT Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztika I. 8. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Beruházási és finanszírozási döntések
 Beruházási és finanszírozási döntések Dr. Farkas Szilveszter PhD, egyetemi docens BGF, PSZK, Pénzügy Intézeti Tanszék farkas.szilveszter@pszfb.bgf.hu, http://dr.farkasszilveszter.hu Tematika és tananyag
Beruházási és finanszírozási döntések Dr. Farkas Szilveszter PhD, egyetemi docens BGF, PSZK, Pénzügy Intézeti Tanszék farkas.szilveszter@pszfb.bgf.hu, http://dr.farkasszilveszter.hu Tematika és tananyag
Vállalkozási finanszírozás kollokvium
 Harsányi János Főiskola Gazdaságtudományok tanszék Vállalkozási finanszírozás kollokvium F Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 43 50 pont jeles 35 42 pont jó 27 34 pont közepes 19 26
Harsányi János Főiskola Gazdaságtudományok tanszék Vállalkozási finanszírozás kollokvium F Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 43 50 pont jeles 35 42 pont jó 27 34 pont közepes 19 26
Vállalkozási finanszírozás kollokvium
 Harsányi János Főiskola Gazdaságtudományok tanszék Vállalkozási finanszírozás kollokvium Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 47 55 pont jeles 38 46 pont jó 29 37 pont közepes 20 28
Harsányi János Főiskola Gazdaságtudományok tanszék Vállalkozási finanszírozás kollokvium Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 47 55 pont jeles 38 46 pont jó 29 37 pont közepes 20 28
Valós függvények tulajdonságai és határérték-számítása
 EL 1 Valós függvények tulajdonságai és határérték-számítása Az ebben a részben szereplő függvények értelmezési tartománya legyen R egy részhalmaza. EL 2 Definíció: zérushely Az f:d R függvénynek zérushelye
EL 1 Valós függvények tulajdonságai és határérték-számítása Az ebben a részben szereplő függvények értelmezési tartománya legyen R egy részhalmaza. EL 2 Definíció: zérushely Az f:d R függvénynek zérushelye
optimal investment for balanced performance balance abszolút hozam portfólió
 2015 optimal investment for balanced performance balance abszolút hozam portfólió GFX Balance Abszolút Hozamú Portfólió Intelligens vagyonkezelés A Balance Abszolút Hozamú Portfólió célja, hogy aktív befektetési
2015 optimal investment for balanced performance balance abszolút hozam portfólió GFX Balance Abszolút Hozamú Portfólió Intelligens vagyonkezelés A Balance Abszolút Hozamú Portfólió célja, hogy aktív befektetési
Intelligent investment for Individual investors. TREND Optimum. Abszolút Hozamú Portfólió
 2015 Intelligent investment for Individual investors TREND Optimum Abszolút Hozamú Portfólió GFX T TREND Optimum Abszolút Hozamú Portfólió Intelligens vagyonkezelés A TREND Optimum Abszolút Hozamú Portfólió
2015 Intelligent investment for Individual investors TREND Optimum Abszolút Hozamú Portfólió GFX T TREND Optimum Abszolút Hozamú Portfólió Intelligens vagyonkezelés A TREND Optimum Abszolút Hozamú Portfólió
14 A Black-Scholes-Merton modell. Options, Futures, and Other Derivatives, 8th Edition, Copyright John C. Hull
 14 A Black-choles-Merton modell Copyright John C. Hull 01 1 Részvényárak viselkedése (feltevés!) Részvényár: μ: elvárt hozam : volatilitás Egy rövid Δt idő alatt a hozam normális eloszlású véletlen változó:
14 A Black-choles-Merton modell Copyright John C. Hull 01 1 Részvényárak viselkedése (feltevés!) Részvényár: μ: elvárt hozam : volatilitás Egy rövid Δt idő alatt a hozam normális eloszlású véletlen változó:
y ij = µ + α i + e ij
 Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Döntési rendszerek I.
 Döntési rendszerek I. SZTE Informatikai Intézet Számítógépes Optimalizálás Tanszék Készítette: London András 3. Gyakorlat Egy újságárus 20 centért szerez be egy adott napilapot a kiadótól és 25-ért adja
Döntési rendszerek I. SZTE Informatikai Intézet Számítógépes Optimalizálás Tanszék Készítette: London András 3. Gyakorlat Egy újságárus 20 centért szerez be egy adott napilapot a kiadótól és 25-ért adja
Tőkepiaci árfolyamok modellje és a hatékony piacok elmélete. Molnár Márk 2006. március 8.
 Tőkepiaci árfolyamok modellje és a hatékony piacok elmélete Molnár Márk 2006. március 8. Tartalom A tőkepiaci árfolyamok modellje (CAPM) Hatékony piacok elmélete (EMH) 2 Miért tart minden befektető piaci
Tőkepiaci árfolyamok modellje és a hatékony piacok elmélete Molnár Márk 2006. március 8. Tartalom A tőkepiaci árfolyamok modellje (CAPM) Hatékony piacok elmélete (EMH) 2 Miért tart minden befektető piaci
Kockázatkezelés és biztosítás 1. konzultáció 2. rész
 Kockázatkezelés és biztosítás 1. konzultáció 2. rész Témák 1) A kockázatkezelés eszközei 2) A kockázatkezelés szakmai területei 3) A kockázatelemzés nem holisztikus technikái 4) Kockázatfinanszírozás 5)
Kockázatkezelés és biztosítás 1. konzultáció 2. rész Témák 1) A kockázatkezelés eszközei 2) A kockázatkezelés szakmai területei 3) A kockázatelemzés nem holisztikus technikái 4) Kockázatfinanszírozás 5)
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/91/106534674.jpg) [Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
[Biomatematika 2] Orvosi biometria Bódis Emőke 2016. 04. 25. J J 9 Korrelációanalízis Regresszióanalízis: hogyan változik egy vizsgált változó értéke egy másik változó változásának függvényében. Korrelációs
STATISZTIKAI PROBLÉMÁK A
 STATISZTIKAI PROBLÉMÁK A HULLÁMTÉR REPRODUKCIÓ TERÜLETÉN 2012. május 3., Budapest Firtha Gergely PhD hallgató, Akusztikai Laboratórium BME Híradástechnikai Tanszék firtha@hit.bme.hu Tartalom A hangtér
STATISZTIKAI PROBLÉMÁK A HULLÁMTÉR REPRODUKCIÓ TERÜLETÉN 2012. május 3., Budapest Firtha Gergely PhD hallgató, Akusztikai Laboratórium BME Híradástechnikai Tanszék firtha@hit.bme.hu Tartalom A hangtér
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
4. Az A és B események egymást kizáró eseményeknek vagy idegen (diszjunkt)eseményeknek nevezzük, ha AB=O
 1. Mit nevezünk elemi eseménynek és eseménytérnek? A kísérlet lehetséges kimeneteleit elemi eseményeknek nevezzük. Az adott kísélethez tartozó elemi események halmazát eseménytérnek nevezzük, jele: X 2.
1. Mit nevezünk elemi eseménynek és eseménytérnek? A kísérlet lehetséges kimeneteleit elemi eseményeknek nevezzük. Az adott kísélethez tartozó elemi események halmazát eseménytérnek nevezzük, jele: X 2.
ESZKÖZALAP BEFEKTETÉSI POLITIKA TARTALMÁNAK MEGFELELŐSÉGÉT ELLENŐRZŐ LISTA
 ESZKÖZALAP BEFEKTETÉSI POLITIKA TARTALMÁNAK MEGFELELŐSÉGÉT ELLENŐRZŐ LISTA Biztosító neve: Eszközalap neve: Az ellenőrző lista készítésének időpontja: Az ellenőrző lista készítője: 1. ESZKÖZALAP ELNEVEZÉSE
ESZKÖZALAP BEFEKTETÉSI POLITIKA TARTALMÁNAK MEGFELELŐSÉGÉT ELLENŐRZŐ LISTA Biztosító neve: Eszközalap neve: Az ellenőrző lista készítésének időpontja: Az ellenőrző lista készítője: 1. ESZKÖZALAP ELNEVEZÉSE
1. tétel. Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség.
 1. tétel Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség. A valószínűségszámítás tárgya: véletlen tömegjelenségek vizsgálata. véletlen: a kísérlet kimenetelét
1. tétel Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség. A valószínűségszámítás tárgya: véletlen tömegjelenségek vizsgálata. véletlen: a kísérlet kimenetelét
Optimalizálás alapfeladata Legmeredekebb lejtő Lagrange függvény Log-barrier módszer Büntetőfüggvény módszer 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
0,424 0,576. f) P (X 2 = 3) g) P (X 3 = 1) h) P (X 4 = 1 vagy 2 X 2 = 2) i) P (X 7 = 3, X 4 = 1, X 2 = 2 X 0 = 2) j) P (X 7 = 3, X 4 = 1, X 2 = 2)
 Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem.
 Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem. Elemi esemény: a kísérlet egyes lehetséges egyes lehetséges kimenetelei.
Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem. Elemi esemény: a kísérlet egyes lehetséges egyes lehetséges kimenetelei.
Kutatásmódszertan és prezentációkészítés
 Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
A valós számok halmaza
 VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
Matematikai statisztika I. témakör: Valószínűségszámítási ismétlés
 Matematikai statisztika I. témakör: Valószínűségszámítási ismétlés Elek Péter 1. Valószínűségi változók és eloszlások 1.1. Egyváltozós eset Ismétlés: valószínűség fogalma Valószínűségekre vonatkozó axiómák
Matematikai statisztika I. témakör: Valószínűségszámítási ismétlés Elek Péter 1. Valószínűségi változók és eloszlások 1.1. Egyváltozós eset Ismétlés: valószínűség fogalma Valószínűségekre vonatkozó axiómák
Kiválasztás. A változó szerint. Rangok. Nem-paraméteres eljárások. Rang: Egy valamilyen szabály szerint felállított sorban elfoglalt hely.
 Kiválasztás A változó szerint Egymintás t-próba Mann-Whitney U-test paraméteres nem-paraméteres Varianciaanalízis De melyiket válasszam? Kétmintás t-próba Fontos, hogy mindig a kérdésnek és a változónak
Kiválasztás A változó szerint Egymintás t-próba Mann-Whitney U-test paraméteres nem-paraméteres Varianciaanalízis De melyiket válasszam? Kétmintás t-próba Fontos, hogy mindig a kérdésnek és a változónak
Loss Distribution Approach
 Modeling operational risk using the Loss Distribution Approach Tartalom»Szabályozói környezet»modellezési struktúra»eseményszám eloszlás»káreloszlás»aggregált veszteségek»további problémák 2 Szabályozói
Modeling operational risk using the Loss Distribution Approach Tartalom»Szabályozói környezet»modellezési struktúra»eseményszám eloszlás»káreloszlás»aggregált veszteségek»további problémák 2 Szabályozói
Mikroökonómia II. B. ELTE TáTK Közgazdaságtudományi Tanszék. 6. hét AZ IDŽ KÖZGAZDASÁGTANA, 1. rész
 MIKROÖKONÓMIA II. B ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia II. B AZ IDŽ KÖZGAZDASÁGTANA, 1. rész Készítette: Szakmai felel s: 2011. február A tananyagot készítette: Jack Hirshleifer, Amihai
MIKROÖKONÓMIA II. B ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia II. B AZ IDŽ KÖZGAZDASÁGTANA, 1. rész Készítette: Szakmai felel s: 2011. február A tananyagot készítette: Jack Hirshleifer, Amihai
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 2 II. A valószínűségi VÁLTOZÓ És JELLEMZÉsE 1. Valószínűségi VÁLTOZÓ Definíció: Az leképezést valószínűségi változónak nevezzük, ha
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 2 II. A valószínűségi VÁLTOZÓ És JELLEMZÉsE 1. Valószínűségi VÁLTOZÓ Definíció: Az leképezést valószínűségi változónak nevezzük, ha
