A csigáról és annak működéséről
|
|
|
- Jázmin Jónásné
- 8 évvel ezelőtt
- Látták:
Átírás
1 A csigáról és annak működéséről Az alábbiakban az ismert egyszerű géppel: a csigával foglalkozunk egy kicsit. Úgy tűnik, az történt, hogy valamit magától értetődőnek vettünk, ami nem is az. Most erről lesz szó. Kezdjük egy szép ábrával ld.. ábra, melynek forrása: [ ]!. ábra Itt csigákból készített egyszerű gépek működésének lényegét tanulmányozhatjuk. Az ezzel kapcsolatos lényeges tudnivalók az alábbiak..) A csiga csak az erő irányát változtatja meg, nagysága ugyanaz marad, a kötél mentén..) Fz s Fl h, azaz munkavégzést nem takaríthatunk meg az egyszerű gépek használatával, mert a kisebb F z erőkifejtésért cserébe hosszabb s úton mozdul el a húzóerő támadáspontja, az F l teher h magasságba való felemelésekor. Minket itt az első kérdés foglalkoztat: Honnan tudhatjuk, hogy a csigán átvetett kötélben a húzóerő mindenhol ugyanaz? A gyors válasz: magunktól sehonnan. A Fizika éppen az ilyen kérdések megválaszolására szakosodott. Nézzük meg, mit mond nekünk erről! Az.) pont állításának igazolására forduljunk először a kísérletek felé! [ ] szerint: ha úgy járunk el, hogy az. ábra első részábráján lévő bal oldali kampóhoz egy erőmérőt erősítünk, akkor a dinamométer a súly nagyságával egyező nagyságú erőt fog mutatni. Hozzáteszi, hogy Ez az igazolás azt is mutatja, hogy állócsiga és fonál segítségével a nehézségi erő irányát az erő nagyságának megváltoztatása nélkül bármilyen irányba átvihetjük. Nem feledkezhetünk meg a reális testek esetén fellépő ellenállásokról, melyek az előbb ismertetett ideális esettől való eltérést okozhatják. Az ideális eset itt azt jelenheti, hogy egy laboratóriumban van kellően hajlékony fonál, sima és finoman csapágyazott csiga.
2 Meglehet, épp ezen a ponton történt meg velünk az a csúfság, hogy azt gondolhattuk: ha kísérletileg bebizonyosodott, hogy az.) pont állítása igaz, akkor ezt innentől nem megkérdőjelezendő tényként kell, hogy kezeljük, azaz elfogadjuk. Most nézzük meg, hogyan lehetne az.) pont igazát elméletileg, azaz spekulatíve belátni! Ehhez [ 3 ] - nál is találunk útmutatást. Tekintsük az innen származó. ábrát!. ábra Az a.) ábrán feltüntetett r sugarú korongot C középpontjában síkbeli csuklóval kapcsoljuk valamely mozdulatlan szerkezethez A korongon kötelet vetünk át, rendesen a korong kerületén végigmenő és erre a célra szolgáló vályúban, majd a kötél két szárára húzóerőt működtetünk. Lehet pl., hogy a bal oldali kötélszárra egy ismert Q súly van felfüggesztve. Kérdés: mekkora P erőt kell működtetnünk a másik szárra, ha a súlyt emelni akarjuk? Legyen a kötél és a csiga közt fellépő súrlódás olyan mértékű, hogy a kötél nem csúszik el a csigához képest. Ekkor a csiga és az ábrán megjelölt A és B pontok közt a csigához simuló kötéldarab egy merev testnek tekinthető, melyre a megjelölt ismert Q erő és az ismeretlen P erő hat, amint azt a b.) ábrarészen feltüntettük. Nyugalomban lesz a csiga, ha a rá ható erők egyensúlyban vannak. Figyelembe véve tehát a C csuklóerőt is, nyugalom esetén: Q, P,C 0. A C pontra vonatkozó nyomatéki egyenlet: rq rp 0. Innen P Q. Súrlódásmentesnek képzelt csukló esetében ennél csak valamivel is nagyobb P erő már mozgásba hozza a csigát és a Q teher emelkedni fog. Csiga esetében tehát a teherrel legalább egyenlő nagyságú erőt kell kifejtenünk az emeléshez. A fenti idézet mondandónk szempontjából kritikus részét vastag dőlt betűkkel emeltük ki. Most megmutatjuk, hogy van egy más feltevésekre alapozott érvelés is, mellyel szintén kiadódik a fenti P Q összefüggés. A most következő idézetet ismét [ 3 ] - ból vettük. Tekintsük a 3. ábrát!
3 3 3. ábra Az ábrán mozdíthatatlan, r sugarú korongot vagy hengert látunk, amelyen át van vetve egy elhanyagolható vastagságú, súlytalan, teljesen hajlékony kötél. A kötél egyik végére ismert S 0 erő hat. Mekkora S erőt kell működtetnünk a kötél másik végére, ha azt kívánjuk, hogy a kötél ne csússzék el? Tegyük fel, hogy a henger és a kötél teljesen simák, tehát súrlódás nincs. Ekkor a henger a kötélre az érintkezés minden pontjában csak normális, vagyis sugárirányú elemi dn erőt fejt ki. Ezek rendszerét ( dn ) - nel jelöljük. A kötéldarab nyugalmi állapota miatt a reá ható erők egyensúlyban vannak. Így S 0,S, dn 0. Az O középpontra felírható nyomatéki egyenletből: 0 S S. ( * ) Most hasonlítsuk össze a két eset feltételeit, melyek mindegyikénél azt kaptuk, hogy a korongra felfutó és az arról lefutó kötélágban egyforma nagyságú húzóerő ébred, azaz fennáll az.) pontbeli állítás; ezek: ~ a korong : csuklós ( elforgatható ) a korong mozdíthatatlan; ~ a kötél és a csiga közt : ( elegendően nagy ) súrlódás lép fel súrlódás nem lép fel. Úgy tűnik, hogy ezek egymás ellentétei, és mégis kijön ugyanaz a ( * ) eredmény. Minthogy ~ a korong és a csukló közti súrlódás jelensége: a csapsúrlódás, valamint ~ a korong és a kötél közti súrlódás: a kötélsúrlódás, így látjuk, hogy a csiga működési feltételeit jórészt e kétféle súrlódási jelenség megléte, ill. annak mértéke határozza meg. Ezek után már nem lepődik meg az ember, ha valaki úgy dönt, hogy a ( * ) eredményt kísérleti tapasztalati tényként könyveli el, ami számára ekkor már nem igényel különösebb magyarázatot. Persze, az Olvasó dönthet másként is; ekkor számára ajánlható a [ 3 ] - ban található további anyagrészek tanulmányozása is. Ezek után belátható, hogy a csiga működése nem igazán nyilvánvaló, valamint a gyakran tapasztalható szokásos elintézése nem magától értetődő. Most nézzünk néhány példát, hogy egy - egy konkrét feladatban hogyan oldják meg a fenti problémát: mi a csiga - kérdés szokásos elintézése!
4 4. Példa [ 4 ]. 4. ábra A 4. ábrán vázolt szerkezet külső reakcióinak a meghatározásakor úgy veszik, hogy a csiga és a kötél a szerkezet része; ezek egy adott helyzetű G vektorú külső erőt működtetnek a szerkezetre. A belső reakciók pl. a csapokban ébredő támasztóerők meghatározása érdekében a szerkezetet majd részeire bontják ld. 5. ábra! Ekkor már fontos szerepet kap a csiga is, a mondott tulajdonságaival. 5. ábra. Példa [ 5 ]. Ez az egyik kedvencünk ld. a 6. ábrát is! Az l hosszúságú, nem nyúló, hajlékony ACB fonál végeit fixen rögzítjük az A és B pontokban, melyek vízszintes és függőleges távolságai egymástól a és b. A fonálra a P terhet egy C csigával adjuk át, melynek súlyát és súrlódását elhanyagoljuk. 6. ábra
5 5 Határozzuk meg az α és β szögeket, a fonál - ágakban ébredő erők nagyságát, valamint a ξ távolságot, a rendszer egyensúlyi helyzetében! Adott: a, b, l; P. Keresett: α, β, T, T, ξ. Megoldás Mivel az ideális csiga nem változtatja meg a fonálerő nagyságát, így T ' T. ( ) A vízszintes vetületi egyenlet: X Tcos 90 T ' cos ( ) Most ( ) és ( ) - vel, valamint a cos 90 sin, cos 90 sin összefüggésekkel: T sin sin 0, ahonnan T > 0 miatt. ( 3 ) A függőleges vetületi egyenlet: Y P Tcos T' cos 0. ( 4 ) Most ( ), ( 3 ), ( 4 ) - gyel: P T. ( 5 ) cos Felhasználva, hogy ( 3 ) - mal is: cos cos l a, l ( 6 ) innen l a arccos. ( 6 / ) l Majd ( 5 ) és ( 6 ) - tal: P l T P, l a l a l tehát ( ) - gyel is:
6 6 l T ' T P. l a ( 7 ) Továbbá a 6. ábra szerint is: AA ' lcos b tg tg lsin b tg b tg b a b lsin l sin, lsin lcos l a tehát a b. l a ( 8 ) A ( 8 ) képletből kiolvasható, hogy b = 0 esetén a csiga középen van nyugalomban, valamint az is, hogy minél nagyobb b, annál közelebb van a csiga a bal oldali csuklóhoz. A. Példa megoldásához ld. még a [ 6 ] munkát is! 3. Példa [ 7 ] Adott az m tömegű golyó, amit a 7. ábra szerinti elrendezésben függesztünk fel. Az állócsiga jobb oldali kötélága a függőlegessel α szöget zár be. Határozzuk meg a kötélerőket és a csiga csapján ébredő reakcióerőt ~ szerkesztéssel, ~ számítással! Megoldás 7. ábra a.) Szerkesztés Egy átmetszéssel bontsuk a szerkezetet két részre! Az eredményt a 8. ábra szemlélteti. Ennek alsó részén azt szemlélhetjük, hogy a G = mg súly és az S kötélerő kielégítik a két erő egyensúlyáról szóló axiómát, ha S m g.
7 7 A 8. ábra felső részén a csiga, ill. a kötél egyensúlyát szemlélhetjük: a kötélerők adott hatásvonalúak, a csuklóerő hatásvonalának pedig adott egy pontja. 8. ábra 9. ábra A 9. ábra bal oldali részén azt szemlélhetjük, hogy a három erő egyensúlyáról szóló tétel egyik állítása szerint a kötélre ható három ( eredő ) erő hatásvonalának egy pontban kell metsződnie; ez a pont a csiga középpontján kívül van, a csiga véges nagyságú sugara miatt. A jobb oldali ábrarészen pedig azt szemlélhetjük, hogy az egyensúly másik feltétele az erőkre folytonos nyílértelemmel rajzolt zárt vektorháromszög. Ennek szerkesztése: ~ a felvett erőmértéknek megfelelően felhordjuk az S = mg nagyságú függőleges szakaszt, és rárajzoljuk a súlyerő nyílértelmét; ~ az előbbi szakaszhoz képest α szöggel egyenest rajzolunk, annak alsó végpontján keresztül; ~ a súlyerő vektorának kezdőpontján keresztül egyenest rajzolunk, az S,S metszéspontját a csiga középpontjával összekötő egyenessel párhuzamosan; ~ felhordjuk a folytonos nyílértelemnek megfelelő nyilakat; ~ a vektorábrán ( Krafteck ) kapott S és A eredményvektorokat visszarajzoljuk az elrendezési rajzra ( Lageplan ). Ezzel a szerkesztéses megoldást befejeztük. b.) Számítás A szerkesztésnél is alkalmazott átmetszés eredményét a 0. ábra szemlélteti. A számítás során meghatározandó négy ismeretlen: S, S, A, β.
8 8 0. ábra A függőleges kötélág, ill. a golyó egyensúlya ld. a bal oldali ábrarészt! : F y S m g 0 S m g. ( ) A jobb oldali ábrarész is kétféleképpen értelmezhető: a.) az ábra a kötél végein ható S, S erő - vektorokat, valamint a kötélre a csiga - horony köríve mentén ható, itt nem ábrázolt megoszló erőrendszer A eredőjének összetevőkre bontását szemlélteti; b.) az ábra a csigára ható erőket szemlélteti, úgy, hogy az S, S erő - vektorokat egy - egy r sugarú emelő - karral az A csuklóhoz mereven rögzítettnek képzeljük. A kötél által a csigára kifejtett, ív mentén megoszló erőrendszer itt sincs ábrázolva. Az egyensúlyi egyenletek az alábbiak. ~ Nyomatéki egyenlet az M csapágy - középpontra: M M S r S r 0 S S. ( ) Most ( ) és ( ) - vel: S S m g. ( 3 ) ~ Vízszintes vetületi egyenlet: F x A x S sin 0 A S sin. x ( 4 ) Most ( 3 ) és ( 4 ) - gyel: A mgsin. ( 5 ) x ~ Függőleges vetületi egyenlet: F y A y S S cos 0 A S S cos. y ( 6 ) Most ( 3 ) és ( 6 ) - tal: Ay mg cos. ( 7 ) A támaszerő nagysága Pitagorász tételével:
9 9 A A A ; ( 8 ) x y majd ( 5 ), ( 7 ), ( 8 ) - cal: A mgsin mg cos mg sin cos cos tehát mg cos, A mg cos. ( 9 ) A támaszerőnek a függőlegessel bezárt szögére: Ax tg. ( 0 ) A y Ezután ( 5 ), ( 7 ), ( 0 ) - zel: m g sin sin tg, mg cos cos tehát sin tg. cos ( ) Most alkalmazzuk az alábbi trigonometriai összefüggéseket [ 8 ] : cos cos cos ; ( ) sin tg. cos ( 3 ) Továbbá ( 9 ) és ( ) - vel: A mg cos. ( 4 ) Majd ( ) és ( 3 ) - mal: tg tg, innen pedig. ( 5 ) Ezzel a számításos megoldást befejeztük.
10 0 Megjegyzések: M. Amikor olyanokat találunk ki, hogy a csiga és a csigához simuló kötéldarab egy merev testnek tekinthető, az némiképp kimódolt, mesterkélt eljárásnak mondható. Akárhonnan is nézzük, ez a történet legalábbis elgondolkodtató; így talán érthető, hogy miért volt ez a kissé furcsa eszmefuttatás. M. Említsük meg, hogy a virtuális munka elve ld.: [ ]! szerint, a. ábra jelöléseivel az állócsiga esetében: PsQs 0, (! ) ahonnan rögtön P Q következik. Itt kihasználtuk a fonál nyújthatatlanságát is, vagyis, hogy a P erő támadáspontjának a P erő irányába eső δs elmozdulásánál a Q teher is δs - sel emelkedik. M3. Ha figyelembe vesszük, hogy s r, (!! ) akkor (! ) és (!! ) képletekkel a PrQr 0 Pr Qr 0 (!!! ) nyomatéki egyensúlyt kifejező egyenlet adódik. Ez némileg gyógyír sebeinkre. M4. A ( ) nyomatéki egyensúlyi egyenlet azért ilyen egyszerű alakú, mert ideális kötéllel és csigával dolgozunk, azaz feltételezzük ~ a kötél hajlékonyságát, vagyis, hogy a kötélágakban nem lép fel hajlítónyomaték; ~ a csiga csapjának súrlódásmentességét, vagyis, hogy nem lép fel a csapsúrlódás nyomatéka. Ezzel kapcsolatban ld. pl. [ 6 ] - ot! M5. A csigák, csigasorok mint egyszerű gépek hatásfokával, ill. veszteségtényezőjével kapcsolatban ld. pl.: [ 9 ] - et! Irodalom: [ ] [ ] Budó Ágoston ~ Pócza Jenő: Kísérleti fizika I. kötet 6. kiadás, Tankönyvkiadó, Budapest, 975.
11 [ 3 ] Cholnoky Tibor: Mechanika I. kötet: Statika Tankönyvkiadó, Budapest, 969. [ 4 ] [ 5 ] V. M: Starzhinskii: An Advanced Course of Theoretical Mechanics MIR Publishers, Moscow, 98. [ 6 ] Muttnyánszky Ádám: Statika 8. kiadás, Tankönyvkiadó, Budapest, 964. [ 7 ] [ 8 ] I. N. Bronstejn ~ K. A. Szemengyajev: Matematikai zsebkönyv Műszaki Könyvkiadó, Budapest, több kiadásban [ 9 ] Szerk. Boldizsár Tibor: Bányászati kézikönyv. I. kötet Műszaki Könyvkiadó, Budapest, 956. Sződliget, 00. február 8. Összeállította: Galgóczi Gyula mérnöktanár
Egy érdekes statikai - geometriai feladat
 1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
T s 2 képezve a. cos q s 0; 2. Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról
 Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról Úgy találjuk, hogy a kötelek statikájának népszerűsítése egy soha véget nem érő feladat. Annyi szép dolog tárháza
Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról Úgy találjuk, hogy a kötelek statikájának népszerűsítése egy soha véget nem érő feladat. Annyi szép dolog tárháza
Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó.
![Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó.](/thumbs/92/108783591.jpg) 1 Végein függesztett rúd egyensúlyi helyzete Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. A feladat Ehhez tekintsük a 2. ábrát is! 1. ábra forrása:
1 Végein függesztett rúd egyensúlyi helyzete Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. A feladat Ehhez tekintsük a 2. ábrát is! 1. ábra forrása:
Egymásra támaszkodó rudak
 1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
A magától becsukódó ajtó működéséről
 1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
Felső végükön egymásra támaszkodó szarugerendák egyensúlya
 1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
Egy érdekes mechanikai feladat
 1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
Egy forgáskúp metszéséről. Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben.
 Egy forgáskúp metszéséről Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben. Az O csúcsú, O tengelyű, γ félnyílásszögű kúpot az ( XY ) sík itt két alkotóban
Egy forgáskúp metszéséről Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben. Az O csúcsú, O tengelyű, γ félnyílásszögű kúpot az ( XY ) sík itt két alkotóban
Kiegészítés a három erő egyensúlyához
 1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
Rönk kiemelése a vízből
 1 Rönk kiemelése a vízből Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot 1. ábra. A feladat 1. ábra forrása: [ 1 ] Egy daru kötél segítségével lassan emeli ki a vízből a benne úszó gerendát
1 Rönk kiemelése a vízből Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot 1. ábra. A feladat 1. ábra forrása: [ 1 ] Egy daru kötél segítségével lassan emeli ki a vízből a benne úszó gerendát
Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal.
![Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal.](/thumbs/92/110379255.jpg) 1 Egy érdekes statikai feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. A feladat A szabályos n - szög alakú, A, B, C, csúcsú lap az A csúcsán egy sima függőleges fal - hoz támaszkodik,
1 Egy érdekes statikai feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. A feladat A szabályos n - szög alakú, A, B, C, csúcsú lap az A csúcsán egy sima függőleges fal - hoz támaszkodik,
A kötélsúrlódás képletének egy általánosításáról
 1 A kötélsúrlódás képletének egy általánosításáról Sok korábbi dolgozatunkban foglalkoztunk kötélstatikai feladatokkal. Ez a mostani azon - ban még nem került szóba. A feladat: az egyenes körhengerre feltekert,
1 A kötélsúrlódás képletének egy általánosításáról Sok korábbi dolgozatunkban foglalkoztunk kötélstatikai feladatokkal. Ez a mostani azon - ban még nem került szóba. A feladat: az egyenes körhengerre feltekert,
Ellipszis átszelése. 1. ábra
 1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
Síkbeli csuklós rúdnégyszög egyensúlya
 Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1.
![Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1.](/thumbs/27/12197964.jpg) 1 Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Feladat Egy G gépkocsi állandó v 0 nagyságú sebességgel egyenes úton
1 Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Feladat Egy G gépkocsi állandó v 0 nagyságú sebességgel egyenes úton
6. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
Egy geometriai szélsőérték - feladat
 1 Egy geometriai szélsőérték - feladat A feladat: Szerkesztendő egy olyan legnagyobb területű háromszög, melynek egyik csúcsa az a és b féltengelyeivel adott ellipszis tetszőlegesen felvett pontja. Keresendő
1 Egy geometriai szélsőérték - feladat A feladat: Szerkesztendő egy olyan legnagyobb területű háromszög, melynek egyik csúcsa az a és b féltengelyeivel adott ellipszis tetszőlegesen felvett pontja. Keresendő
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
Egy háromlábú állvány feladata. 1. ábra forrása:
 1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
EGYSZERŰ GÉPEK. Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét.
 EGYSZERŰ GÉPEK Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét. Az egyszerű gépekkel munkát nem takaríthatunk meg, de ugyanazt a munkát kisebb
EGYSZERŰ GÉPEK Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét. Az egyszerű gépekkel munkát nem takaríthatunk meg, de ugyanazt a munkát kisebb
Két statikai feladat
 1 Két statikai feladat Az interneten találtuk az [ 1 ] feladatgyűjteményt és benne két érdekes feladatot. Úgy tűnik, hasznos lehet megoldásuk, feldolgozásuk. Az 1. feladat nagyon ismerősnek tűnt. Ez nem
1 Két statikai feladat Az interneten találtuk az [ 1 ] feladatgyűjteményt és benne két érdekes feladatot. Úgy tűnik, hasznos lehet megoldásuk, feldolgozásuk. Az 1. feladat nagyon ismerősnek tűnt. Ez nem
A síkbeli Statika egyensúlyi egyenleteiről
 1 A síkbeli Statika egyensúlyi egyenleteiről Statikai tanulmányaink egyik mérföldköve az egyensúlyi egyenletek belátása és sikeres alkalmazása. Most egy erre vonatkozó lehetséges tanulási / tanítási útvonalat
1 A síkbeli Statika egyensúlyi egyenleteiről Statikai tanulmányaink egyik mérföldköve az egyensúlyi egyenletek belátása és sikeres alkalmazása. Most egy erre vonatkozó lehetséges tanulási / tanítási útvonalat
Fa rudak forgatása II.
 Fa rudak forgatása II. Dolgozatunk I. részében egy speciális esetre oldottuk meg a kitűzött feladatokat. Most egy általánosabb elrendezés vizsgálatát végezzük el. A számítás a korábbi úton halad, ügyelve
Fa rudak forgatása II. Dolgozatunk I. részében egy speciális esetre oldottuk meg a kitűzött feladatokat. Most egy általánosabb elrendezés vizsgálatát végezzük el. A számítás a korábbi úton halad, ügyelve
Egy általánosabb súrlódásos alapfeladat
 Egy általánosabb súrlódásos alapfeladat Az előző dolgozatunkban címe: Egy súrlódásos alapfeladat, jele: ( E D ) tárgyalt probléma általánosítása az alábbi, melynek forrása [ 1 ]. Tekintsük az 1. ábrát!
Egy általánosabb súrlódásos alapfeladat Az előző dolgozatunkban címe: Egy súrlódásos alapfeladat, jele: ( E D ) tárgyalt probléma általánosítása az alábbi, melynek forrása [ 1 ]. Tekintsük az 1. ábrát!
Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) 1. ábra
 Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) Egy korábbi dolgozatunkban címe: Két egyenes körhenger a merőlegesen metsződő tengelyű körhengerek áthatási feladatával foglalkoztunk. Most
Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) Egy korábbi dolgozatunkban címe: Két egyenes körhenger a merőlegesen metsződő tengelyű körhengerek áthatási feladatával foglalkoztunk. Most
Forgatónyomaték mérése I.
 Forgatónyomaték mérése I Bevezetés A forgatónyomaték az erőpár mint statikai alapalakzat jellemzője A nevéből is következően a testekre forgató hatást fejt ki Vektormennyiség, melyet az M = a x F képlettel
Forgatónyomaték mérése I Bevezetés A forgatónyomaték az erőpár mint statikai alapalakzat jellemzője A nevéből is következően a testekre forgató hatást fejt ki Vektormennyiség, melyet az M = a x F képlettel
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I. rész
 Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Lépcső beemelése. Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával.
![Lépcső beemelése. Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával. Lépcső beemelése. Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával.](/thumbs/104/162084051.jpg) 1 Lépcső beemelése Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával. 1. ábra forrása: [ 1 ] Itt példákat látunk előregyártott vasbeton szerkezeti elemek kötéllel / lánccal történő emelésére,
1 Lépcső beemelése Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával. 1. ábra forrása: [ 1 ] Itt példákat látunk előregyártott vasbeton szerkezeti elemek kötéllel / lánccal történő emelésére,
Egy nyíllövéses feladat
 1 Egy nyíllövéses feladat Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. 1. ábra forrása: [ 1 / 1 ] Igencsak tanulságos, ezért részletesen bemutatjuk a megoldását. A feladat Egy sportíjjal nyilat
1 Egy nyíllövéses feladat Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. 1. ábra forrása: [ 1 / 1 ] Igencsak tanulságos, ezért részletesen bemutatjuk a megoldását. A feladat Egy sportíjjal nyilat
1. Feladatok a dinamika tárgyköréből
 1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk, és az elhanyagolható tömegű
1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk, és az elhanyagolható tömegű
A ferde tartó megoszló terheléseiről
 A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát.
 1 Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát. 1. ábra forrása: [ 1 ] Ezen egy út tengelyvonalának egy pontjában tüntették
1 Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát. 1. ábra forrása: [ 1 ] Ezen egy út tengelyvonalának egy pontjában tüntették
Egy sík és a koordinátasíkok metszésvonalainak meghatározása
 1 Egy sík és a koordinátasíkok metszésvonalainak meghatározása Ehhez tekintsük az 1. ábrát! 1. ábra Itt az ( u, v, w ) tengelymetszeteivel adott S síkot látjuk, az Oxyz térbeli derékszögű koordináta -
1 Egy sík és a koordinátasíkok metszésvonalainak meghatározása Ehhez tekintsük az 1. ábrát! 1. ábra Itt az ( u, v, w ) tengelymetszeteivel adott S síkot látjuk, az Oxyz térbeli derékszögű koordináta -
Egy furcsa tartóról. A probléma felvetése. Adott az 1. ábra szerinti kéttámaszú tartó. 1. ábra
 Egy furcsa tartóról Az alábbi probléma ha jól emlékszem tanulói felvetés, melyet tanáruk volt kol - légánk G. A. továbbított. ( Üdv Néked, Nagy Király! ) Hogy a probléma valós - e vagy mondvacsinált, azt
Egy furcsa tartóról Az alábbi probléma ha jól emlékszem tanulói felvetés, melyet tanáruk volt kol - légánk G. A. továbbított. ( Üdv Néked, Nagy Király! ) Hogy a probléma valós - e vagy mondvacsinált, azt
Egy kinematikai feladathoz
 1 Egy kinematikai feladathoz Az [ 1 ] példatárból való az alábbi feladat. Egy bütyök v 0 állandó nagyságú sebességgel halad jobbról balra. Kontúrjának egyenlete a hozzá kötött, vele együtt haladó O 1 xy
1 Egy kinematikai feladathoz Az [ 1 ] példatárból való az alábbi feladat. Egy bütyök v 0 állandó nagyságú sebességgel halad jobbról balra. Kontúrjának egyenlete a hozzá kötött, vele együtt haladó O 1 xy
Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra.
![Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra.](/thumbs/95/123788187.jpg) 1 Tető - feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. 1. ábra forrása: [ 1 ] Most ezt oldjuk meg, részletesen. A feladat szövegének ( saját, hevenyészett
1 Tető - feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. 1. ábra forrása: [ 1 ] Most ezt oldjuk meg, részletesen. A feladat szövegének ( saját, hevenyészett
Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához
 1 Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához Az interneten való nézelődés során találkoztunk az [ 1 ] művel, melyben egy érdekes és fontos feladat pontos(abb) megoldásához
1 Függőleges koncentrált erőkkel csuklóin terhelt csuklós rúdlánc számításához Az interneten való nézelődés során találkoztunk az [ 1 ] művel, melyben egy érdekes és fontos feladat pontos(abb) megoldásához
Lövés csúzlival. Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk ki!
 1 Lövés csúzlival Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. A feladat Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk
1 Lövés csúzlival Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. A feladat Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk
 MECHANIKA I. /Statika/ 1. előadás SZIE-YMM 1. Bevezetés épületek, építmények fizikai hatások, köztük erőhatások részleges vagy teljes tönkremenetel használhatatlanná válás anyagi kár, emberáldozat 1 Cél:
MECHANIKA I. /Statika/ 1. előadás SZIE-YMM 1. Bevezetés épületek, építmények fizikai hatások, köztük erőhatások részleges vagy teljes tönkremenetel használhatatlanná válás anyagi kár, emberáldozat 1 Cél:
Aszimmetrikus nyeregtető ~ feladat 2.
 1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS!
 Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
1. ábra forrása: [ 1 ]
![1. ábra forrása: [ 1 ] 1. ábra forrása: [ 1 ]](/thumbs/103/161454059.jpg) Merev test emelése négy kötéllel Előző dolgozatunkban melynek címe: Lépcső beemelése már foglalkoztunk a témával. Akkor elmondtuk, hogy a négyköteles teheremelés feladata statikailag egyszeresen hatá -
Merev test emelése négy kötéllel Előző dolgozatunkban melynek címe: Lépcső beemelése már foglalkoztunk a témával. Akkor elmondtuk, hogy a négyköteles teheremelés feladata statikailag egyszeresen hatá -
Néhány véges trigonometriai összegről. Határozzuk meg az alábbi véges összegek értékét!, ( 1 ) ( 2 )
 1 Néhány véges trigonometriai összegről A Fizika számos területén találkozhatunk véges számú tagból álló trigonometriai össze - gekkel, melyek a számítások során állnak elő. Ezek értékét kinézhetjük matematikai
1 Néhány véges trigonometriai összegről A Fizika számos területén találkozhatunk véges számú tagból álló trigonometriai össze - gekkel, melyek a számítások során állnak elő. Ezek értékét kinézhetjük matematikai
Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához
 1 Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához Előző dolgozatunkkal melynek címe: A ferde körkúp palástfelszínének meghatározásához már mintegy megágyaztunk a jelen írásnak. Több mindent
1 Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához Előző dolgozatunkkal melynek címe: A ferde körkúp palástfelszínének meghatározásához már mintegy megágyaztunk a jelen írásnak. Több mindent
Fiók ferde betolása. A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát!
 1 Fiók ferde betolása A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát! 1. ábra Itt azt látjuk, hogy egy a x b méretű kis kék téglalapot
1 Fiók ferde betolása A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát! 1. ábra Itt azt látjuk, hogy egy a x b méretű kis kék téglalapot
A visszacsapó kilincs működéséről
 1 A visszacsapó kilincs működéséről A faipari forgácsoló gépek egy részén a munkadarab visszasodródása ellen visszacsapó kilincset / kilincssort alkalmaznak. Ilyen gépek például a felülről vágó körfűrészek
1 A visszacsapó kilincs működéséről A faipari forgácsoló gépek egy részén a munkadarab visszasodródása ellen visszacsapó kilincset / kilincssort alkalmaznak. Ilyen gépek például a felülről vágó körfűrészek
Digitális tananyag a fizika tanításához
 Digitális tananyag a fizika tanításához Ismétlés Erőhatás a testek mechanikai kölcsönhatásának mértékét és irányát megadó vektormennyiség. jele: mértékegysége: 1 newton: erőhatás következménye: 1N 1kg
Digitális tananyag a fizika tanításához Ismétlés Erőhatás a testek mechanikai kölcsönhatásának mértékét és irányát megadó vektormennyiség. jele: mértékegysége: 1 newton: erőhatás következménye: 1N 1kg
A lengőfűrészelésről
 A lengőfűrészelésről Az [ 1 ] tankönyvben ezt írják a lengőfűrészről, működéséről, használatáról: A lengőfűrész árkolásra, csaprések készítésére alkalmazott, 150 00 mm átmérőjű, 3 4 mm vastag, sűrű fogazású
A lengőfűrészelésről Az [ 1 ] tankönyvben ezt írják a lengőfűrészről, működéséről, használatáról: A lengőfűrész árkolásra, csaprések készítésére alkalmazott, 150 00 mm átmérőjű, 3 4 mm vastag, sűrű fogazású
A Maxwell - kerékről. Maxwell - ingának is nevezik azt a szerkezetet, melyről most lesz szó. Ehhez tekintsük az 1. ábrát is!
 1 A Maxwell - kerékről Maxwell - ingának is nevezik azt a szerkezetet, melyről most lesz szó. Ehhez tekintsük az 1. ábrát is! 1. ábra forrása: [ 1 ] Itt azt láthatjuk, hogy egy r sugarú kis hengerre felerősítettek
1 A Maxwell - kerékről Maxwell - ingának is nevezik azt a szerkezetet, melyről most lesz szó. Ehhez tekintsük az 1. ábrát is! 1. ábra forrása: [ 1 ] Itt azt láthatjuk, hogy egy r sugarú kis hengerre felerősítettek
A tűzfalakkal lezárt nyeregtető feladatához
 1 A tűzfalakkal lezárt nyeregtető feladatához Bevezetés Ehhez először tekintsük az 1. ábrát! 1 Itt azt szemlélhetjük, hogy hogyan lehet el - kerülni egy épület tűzfalának eláztatását. A felső ábrarészen
1 A tűzfalakkal lezárt nyeregtető feladatához Bevezetés Ehhez először tekintsük az 1. ábrát! 1 Itt azt szemlélhetjük, hogy hogyan lehet el - kerülni egy épület tűzfalának eláztatását. A felső ábrarészen
Egy mozgástani feladat
 1 Egy mozgástani feladat Előző dolgozatunk melynek jele és címe: ED ~ Ismét az ellipszis egyenleteiről folytatásának tekinthető ez az írás. Leválasztottuk róla, mert bár szorosan kapcsolódnak, más a céljuk.
1 Egy mozgástani feladat Előző dolgozatunk melynek jele és címe: ED ~ Ismét az ellipszis egyenleteiről folytatásának tekinthető ez az írás. Leválasztottuk róla, mert bár szorosan kapcsolódnak, más a céljuk.
Kerekes kút 2.: A zuhanó vödör mozgásáról
 1 Kerekes kút 2.: A zuhanó vödör mozgásáról Előző dolgozatunkban melynek címe: A kerekes kútról a végén azt írtuk, hogy Az elengedett vödör a saját súlya hatására erősen felgyorsulhatott. Ezt személyes
1 Kerekes kút 2.: A zuhanó vödör mozgásáról Előző dolgozatunkban melynek címe: A kerekes kútról a végén azt írtuk, hogy Az elengedett vödör a saját súlya hatására erősen felgyorsulhatott. Ezt személyes
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS-
 A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
Egy másik érdekes feladat. A feladat
 Egy másik érdekes feladat Az előző dolgozatban melynek címe: Egy érdekes feladat az itteninek egy speciális esetét vizsgáltuk. Az általánosabb feladat az alábbi [ 1 ]. A feladat Adott: az ABCD zárt négyszög
Egy másik érdekes feladat Az előző dolgozatban melynek címe: Egy érdekes feladat az itteninek egy speciális esetét vizsgáltuk. Az általánosabb feladat az alábbi [ 1 ]. A feladat Adott: az ABCD zárt négyszög
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
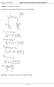 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
Érdekes geometriai számítások Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon
 Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
Mechanika - Versenyfeladatok
 Mechanika - Versenyfeladatok 1. A mellékelt ábrán látható egy jobbmenetű csavar és egy villáskulcs. A kulcsra ható F erővektor nyomatékot fejt ki a csavar forgatása céljából. Az erő támadópontja és az
Mechanika - Versenyfeladatok 1. A mellékelt ábrán látható egy jobbmenetű csavar és egy villáskulcs. A kulcsra ható F erővektor nyomatékot fejt ki a csavar forgatása céljából. Az erő támadópontja és az
A szabályos sokszögek közelítő szerkesztéséhez
 1 A szabályos sokszögek közelítő szerkesztéséhez A síkmértani szerkesztések között van egy kedvencünk: a szabályos n - szög közelítő szerkesztése. Azért vívta ki nálunk ezt az előkelő helyet, mert nagyon
1 A szabályos sokszögek közelítő szerkesztéséhez A síkmértani szerkesztések között van egy kedvencünk: a szabályos n - szög közelítő szerkesztése. Azért vívta ki nálunk ezt az előkelő helyet, mert nagyon
Kecskerágás már megint
 1 Kecskerágás már megint Az interneten találtuk az újabb kecskerágós feladatot 1. ábra. 1. ábra forrása: [ 1 ] A feladat ( kicsit megváltoztatva az eredeti szöveget ) Egy matematikus kecskét tart a kertjében.
1 Kecskerágás már megint Az interneten találtuk az újabb kecskerágós feladatot 1. ábra. 1. ábra forrása: [ 1 ] A feladat ( kicsit megváltoztatva az eredeti szöveget ) Egy matematikus kecskét tart a kertjében.
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Vontatás III. A feladat
 Vontatás III Ebben a részben ázoljuk a ontatási feladat egy lehetséges numerikus megoldási módját Ezt az I részben ismertetett alapegyenletre építjük fel Itt az egy ontatott kerékpár esetét izsgáljuk feladat
Vontatás III Ebben a részben ázoljuk a ontatási feladat egy lehetséges numerikus megoldási módját Ezt az I részben ismertetett alapegyenletre építjük fel Itt az egy ontatott kerékpár esetét izsgáljuk feladat
A csavarvonal axonometrikus képéről
 A avarvonal axonometrikus képéről Miután egyre jobban megy a Graph ingyenes függvény - ábrázoló szoftver használata, kipróbáltuk, hogy tudunk - e vele avarvonalat ábrázolni, axonometrikusan. A válasz:
A avarvonal axonometrikus képéről Miután egyre jobban megy a Graph ingyenes függvény - ábrázoló szoftver használata, kipróbáltuk, hogy tudunk - e vele avarvonalat ábrázolni, axonometrikusan. A válasz:
Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész. Eltérő keresztmetszet - magasságú szarufák esete
 1 Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész Eltérő keresztmetszet - magasságú szarufák esete Az alábbi ábrát találtuk az interneten 1. ábra 1. ábra forrás( ok ): http://www.sema-soft.com/de/forum/files/firstpfettenverschiebung_432.jpg
1 Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész Eltérő keresztmetszet - magasságú szarufák esete Az alábbi ábrát találtuk az interneten 1. ábra 1. ábra forrás( ok ): http://www.sema-soft.com/de/forum/files/firstpfettenverschiebung_432.jpg
Egy kinematikai feladat
 1 Egy kinematikai feladat Valami geometriai dologról ötlött eszembe az alábbi feladat 1. ábra. 1. ábra Adott az a és b egyenes, melyek α szöget zárnak be egymással. A b egyenesre ráfektetünk egy d hosszúságú
1 Egy kinematikai feladat Valami geometriai dologról ötlött eszembe az alábbi feladat 1. ábra. 1. ábra Adott az a és b egyenes, melyek α szöget zárnak be egymással. A b egyenesre ráfektetünk egy d hosszúságú
2.3 Newton törvények, mozgás lejtőn, pontrendszerek
 Keresés (http://wwwtankonyvtarhu/hu) NVDA (http://wwwnvda-projectorg/) W3C (http://wwww3org/wai/intro/people-use-web/) A- (#) A (#) A+ (#) (#) English (/en/tartalom/tamop425/0027_fiz2/ch01s03html) Kapcsolat
Keresés (http://wwwtankonyvtarhu/hu) NVDA (http://wwwnvda-projectorg/) W3C (http://wwww3org/wai/intro/people-use-web/) A- (#) A (#) A+ (#) (#) English (/en/tartalom/tamop425/0027_fiz2/ch01s03html) Kapcsolat
Az elliptikus hengerre írt csavarvonalról
 1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
Henger és kúp metsződő tengelyekkel
 Henger és kúp metsződő tengelyekkel Ebben a dolgozatban egy forgáshenger és egy forgáskúp áthatását tanulmányozzuk abban az egyszerűbb esetben, amikor a két test tengelye egyazon síkban fekszik, vagyis
Henger és kúp metsződő tengelyekkel Ebben a dolgozatban egy forgáshenger és egy forgáskúp áthatását tanulmányozzuk abban az egyszerűbb esetben, amikor a két test tengelye egyazon síkban fekszik, vagyis
Szökőkút - feladat. 1. ábra. A fotók forrása:
 Szökőkút - feladat Nemrégen Gyulán jártunk, ahol sok szép szökőkutat láttunk. Az egyik különösen megtetszett, ezért elhatároztam, hogy megpróbálom elemi módon leírni a ízsugarak, illete az általuk leírt
Szökőkút - feladat Nemrégen Gyulán jártunk, ahol sok szép szökőkutat láttunk. Az egyik különösen megtetszett, ezért elhatároztam, hogy megpróbálom elemi módon leírni a ízsugarak, illete az általuk leírt
Rácsos szerkezetek. Frissítve: Egy kis elmélet: vakrudak
 Egy kis elmélet: vakrudak Az egyik lehetőség, ha két rúd szög alatt találkozik (nem egyvonalban vannak), és nem működik a csomópontra terhelés. Ilyen az 1.ábra C csomópontja. Ekkor az ide befutó mindkét
Egy kis elmélet: vakrudak Az egyik lehetőség, ha két rúd szög alatt találkozik (nem egyvonalban vannak), és nem működik a csomópontra terhelés. Ilyen az 1.ábra C csomópontja. Ekkor az ide befutó mindkét
A Lenz - vektorról. Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra.
![A Lenz - vektorról. Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra. A Lenz - vektorról. Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra.](/thumbs/93/112395793.jpg) 1 A Lenz - vektorról Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra. 1. ábra forrása: [ 1 ] Ez nem régen történt. Meglepett, hogy eddig ez kimaradt. Annál is inkább, mert
1 A Lenz - vektorról Ha jól emlékszem, először [ 1 ] - ben találkoztam a címbeli fogalommal 1. ábra. 1. ábra forrása: [ 1 ] Ez nem régen történt. Meglepett, hogy eddig ez kimaradt. Annál is inkább, mert
Vonatablakon át. A szabadvezeték alakjának leírása. 1. ábra
 1 Vonatablakon át Sokat utazom vonaton, és gyakran elnézem a vonatablakon át a légvezeték(ek) táncát. Már régóta gondolom, hogy le kellene írni ezt a látszólagos mozgást. Most erről lesz szó. Ehhez tekintsük
1 Vonatablakon át Sokat utazom vonaton, és gyakran elnézem a vonatablakon át a légvezeték(ek) táncát. Már régóta gondolom, hogy le kellene írni ezt a látszólagos mozgást. Most erről lesz szó. Ehhez tekintsük
Az egyenes ellipszishenger ferde síkmetszeteiről
 1 Az egyenes ellipszishenger ferde síkmetszeteiről Vegyünk egy a és b féltengelyekkel bíró ellipszist a vezérgörbét, majd az ellipszis O centrumában állítsunk merőlegest az ellipszis síkjára. Ez a merőleges
1 Az egyenes ellipszishenger ferde síkmetszeteiről Vegyünk egy a és b féltengelyekkel bíró ellipszist a vezérgörbét, majd az ellipszis O centrumában állítsunk merőlegest az ellipszis síkjára. Ez a merőleges
Eszközszükséglet: Erők összetevőit bemutató asztal 4 db csigával, nehezékekkel (Varignon-asztal)
 A Varignon-féle asztallal végzett megfigyelések és mérések célkitűzése: Az erők testekre való hatásának és az erők összeadódásának(eredő erő) megfigyelése. Az egyensúlyi erő és az eredő erő kapcsolatának
A Varignon-féle asztallal végzett megfigyelések és mérések célkitűzése: Az erők testekre való hatásának és az erők összeadódásának(eredő erő) megfigyelése. Az egyensúlyi erő és az eredő erő kapcsolatának
DEME FERENC okl. építőmérnök, mérnöktanár
 DEME FERENC okl. építőmérnök, mérnöktanár web-lap : www.sze.hu/~deme e-mail : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA
DEME FERENC okl. építőmérnök, mérnöktanár web-lap : www.sze.hu/~deme e-mail : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA
X i = 0 F x + B x = 0. Y i = 0 A y F y + B y = 0. M A = 0 F y 3 + B y 7 = 0. B x = 200 N. B y =
 1. feladat a = 3 m b = 4 m F = 400 N φ = 60 fok Első lépésként alkossuk meg a számítási modellt. A kényszereket helyettesítsük a bennük ébredő lehetséges erőkkel (második ábra). Az F erő felbontásával
1. feladat a = 3 m b = 4 m F = 400 N φ = 60 fok Első lépésként alkossuk meg a számítási modellt. A kényszereket helyettesítsük a bennük ébredő lehetséges erőkkel (második ábra). Az F erő felbontásával
A ferde szabadforgácsolásról, ill. a csúszóforgácsolásról ismét
 A ferde szabadforgácsolásról, ill. a csúszóforgácsolásról ismét A szabadforgácsolást [ 1 ] az alábbiak szerint definiálja, ill. jellemzi. Ha a forgácsolószerszám élének minden pontjában a forgácsolási
A ferde szabadforgácsolásról, ill. a csúszóforgácsolásról ismét A szabadforgácsolást [ 1 ] az alábbiak szerint definiálja, ill. jellemzi. Ha a forgácsolószerszám élének minden pontjában a forgácsolási
A felcsapódó kavicsról. Az interneten találtuk az alábbi, a hajítás témakörébe tartozó érdekes feladatot 1. ábra.
 1 A felcsapódó kavicsról Az interneten találtuk az alábbi, a hajítás témakörébe tartozó érdekes feladatot 1. ábra. 1. ábra forrása: [ 1 ] Ez azért is érdekes, mert autóvezetés közben már többször is eszünkbe
1 A felcsapódó kavicsról Az interneten találtuk az alábbi, a hajítás témakörébe tartozó érdekes feladatot 1. ábra. 1. ábra forrása: [ 1 ] Ez azért is érdekes, mert autóvezetés közben már többször is eszünkbe
A bifiláris felfüggesztésű rúd mozgásáról
 1 A bifiláris felfüggesztésű rúd mozgásáról A végein fonállal felfüggesztett egyenes rúd részleges erőtani vizsgálatát mutattuk be egy korábbi dolgozatunkban, melynek címe: Forgatónyomaték mérése - I.
1 A bifiláris felfüggesztésű rúd mozgásáról A végein fonállal felfüggesztett egyenes rúd részleges erőtani vizsgálatát mutattuk be egy korábbi dolgozatunkban, melynek címe: Forgatónyomaték mérése - I.
Egy érdekes nyeregtetőről
 Egy érdekes nyeregtetőről Adott egy nyeregtető, az 1 ábra szerinti adatokkal 1 ábra Végezzük el vetületi ábrázolását, az alábbi számszerű adatokkal: a = 10,00 m; b = 6,00 m; c = 3,00 m; α = 45 ; M 1:100!
Egy érdekes nyeregtetőről Adott egy nyeregtető, az 1 ábra szerinti adatokkal 1 ábra Végezzük el vetületi ábrázolását, az alábbi számszerű adatokkal: a = 10,00 m; b = 6,00 m; c = 3,00 m; α = 45 ; M 1:100!
Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt.
![Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt.](/thumbs/27/11117124.jpg) osárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. A feladat Az 1. ábrán [ 1 ] egy tornaterem hosszmetszetét
osárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. A feladat Az 1. ábrán [ 1 ] egy tornaterem hosszmetszetét
Poncelet egy tételéről
 1 Poncelet egy tételéről Már régebben találkoztunk az [ 1 ] műben egy problémával, mostanában pedig a [ 2 ] műben a megoldásával. A probléma lényege: határozzuk meg a egyenletben szereplő α, β együtthatókat,
1 Poncelet egy tételéről Már régebben találkoztunk az [ 1 ] műben egy problémával, mostanában pedig a [ 2 ] műben a megoldásával. A probléma lényege: határozzuk meg a egyenletben szereplő α, β együtthatókat,
Egy variátor - feladat. Az [ 1 ] feladatgyűjteményben találtuk az alábbi feladatot. Most ezt dolgozzuk fel. Ehhez tekintsük az 1. ábrát!
![Egy variátor - feladat. Az [ 1 ] feladatgyűjteményben találtuk az alábbi feladatot. Most ezt dolgozzuk fel. Ehhez tekintsük az 1. ábrát! Egy variátor - feladat. Az [ 1 ] feladatgyűjteményben találtuk az alábbi feladatot. Most ezt dolgozzuk fel. Ehhez tekintsük az 1. ábrát!](/thumbs/104/162808488.jpg) 1 Egy variátor - feladat Az [ 1 ] feladatgyűjteményben találtuk az alábbi feladatot. Most ezt dolgozzuk fel. Ehhez tekintsük az 1. ábrát! A feladat 1. ábra forrás: [ 1 ] Egy súrlódó variátor ( fokozatmentes
1 Egy variátor - feladat Az [ 1 ] feladatgyűjteményben találtuk az alábbi feladatot. Most ezt dolgozzuk fel. Ehhez tekintsük az 1. ábrát! A feladat 1. ábra forrás: [ 1 ] Egy súrlódó variátor ( fokozatmentes
A manzárdtetőről. 1. ábra Forrás: http://upload.wikimedia.org/wikipedia/commons/0/0a/drawing_in_perspective_ of_gambrel-roofed_building.
 A manzárdtetőről Az építőipari tanulók ácsok, magasépítő technikusok részére kötelező gyakorlat a manzárdtetőkkel való foglalkozás. Egy manzárd nyeregtetőt mutat az. ábra.. ábra Forrás: http://upload.wikimedia.org/wikipedia/commons/0/0a/drawing_in_perspective_
A manzárdtetőről Az építőipari tanulók ácsok, magasépítő technikusok részére kötelező gyakorlat a manzárdtetőkkel való foglalkozás. Egy manzárd nyeregtetőt mutat az. ábra.. ábra Forrás: http://upload.wikimedia.org/wikipedia/commons/0/0a/drawing_in_perspective_
KERESZTMETSZETI JELLEMZŐK
 web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
Statikai egyensúlyi egyenletek síkon: Szinusztétel az CB pontok távolságának meghatározására: rcb
 MECHNIK-STTIK (ehér Lajos) 1.1. Példa: Tehergépkocsi a c b S C y x G d képen látható tehergépkocsi az adott pozícióban tartja a rakományt. dott: 3, 7, a 3 mm, b mm, c 8 mm, d 5 mm, G 1 j kn eladat: a)
MECHNIK-STTIK (ehér Lajos) 1.1. Példa: Tehergépkocsi a c b S C y x G d képen látható tehergépkocsi az adott pozícióban tartja a rakományt. dott: 3, 7, a 3 mm, b mm, c 8 mm, d 5 mm, G 1 j kn eladat: a)
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT. Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
A gúla ~ projekthez 2. rész
 1 A gúla ~ projekthez 2. rész Dolgozatunk 1. részében egy speciális esetre a négyzet alapú egyenes gúla esetére írtuk fel és alkalmaztuk képleteinket. Most a tetszőleges oldalszámú szabályos sokszög alakú
1 A gúla ~ projekthez 2. rész Dolgozatunk 1. részében egy speciális esetre a négyzet alapú egyenes gúla esetére írtuk fel és alkalmaztuk képleteinket. Most a tetszőleges oldalszámú szabályos sokszög alakú
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Gépészmérnöki alapszak, Mérnöki fizika ZH, október 10.. CHFMAX. Feladatok (maximum 3x6 pont=18 pont)
 1. 2. 3. Mondat E1 E2 Gépészmérnöki alapszak, Mérnöki fizika ZH, 2017. október 10.. CHFMAX NÉV: Neptun kód: Aláírás: g=10 m/s 2 Előadó: Márkus / Varga Feladatok (maximum 3x6 pont=18 pont) 1) Az l hosszúságú
1. 2. 3. Mondat E1 E2 Gépészmérnöki alapszak, Mérnöki fizika ZH, 2017. október 10.. CHFMAX NÉV: Neptun kód: Aláírás: g=10 m/s 2 Előadó: Márkus / Varga Feladatok (maximum 3x6 pont=18 pont) 1) Az l hosszúságú
ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA
 ALAPOGALMAK ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA Egy testre általában nem egy erő hat, hanem több. Legalább két erőnek kell hatni a testre, ha az erő- ellenerő alaptétel alapján járunk el. A testek vizsgálatához
ALAPOGALMAK ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA Egy testre általában nem egy erő hat, hanem több. Legalább két erőnek kell hatni a testre, ha az erő- ellenerő alaptétel alapján járunk el. A testek vizsgálatához
Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész
![Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész Az R forgató mátrix [ 1 ] - beli képleteinek levezetése: I. rész](/thumbs/57/40130324.jpg) Az R forgató mátri [ ] - beli képleteinek levezetése: I rész Az [ ] forrás kötetében a ( 49 ), ( 50 ) képletek nyilván mint közismertek nem lettek levezetve Minthogy az ottani további számítások miatt
Az R forgató mátri [ ] - beli képleteinek levezetése: I rész Az [ ] forrás kötetében a ( 49 ), ( 50 ) képletek nyilván mint közismertek nem lettek levezetve Minthogy az ottani további számítások miatt
Chasles tételéről. Előkészítés
 1 Chasles tételéről A minap megint találtunk valami érdekeset az interneten. Az [ 1 ] tankönyvet, illetve an - nak fejezetenként felrakott egyetemi internetes változatát. Utóbbi 20. fejezetében volt az,
1 Chasles tételéről A minap megint találtunk valami érdekeset az interneten. Az [ 1 ] tankönyvet, illetve an - nak fejezetenként felrakott egyetemi internetes változatát. Utóbbi 20. fejezetében volt az,
Ehhez tekintsük a 2. ábrát is! A födém és a fal síkját tekintsük egy - egy koordinátasíknak, így a létra tömegközéppontjának koordinátái: ( 2 )
 1 A lecsúszó létra mozgásáról Egy korábbi létrás dolgozatunkban melynek címe: Létra - feladat foglalkoztunk a csak önsúlyával terhelt, függőleges falnak támasztott, vízszintes födémen álló létra egyensúlyá
1 A lecsúszó létra mozgásáról Egy korábbi létrás dolgozatunkban melynek címe: Létra - feladat foglalkoztunk a csak önsúlyával terhelt, függőleges falnak támasztott, vízszintes födémen álló létra egyensúlyá
A kvadratrixról. Ez azt jelenti, hogy itt a görbe egy mozgástani származtatását vesszük elő 1. ábra. 1. ábra
 1 A kvadratrixról A kvadratrix más néven triszektrix nevű síkgörbéről az [ 1 ] és [ 2 ] munkákban is olvashatunk. A keletkezéséről készített animáció itt tekinthető meg: http://hu.wikipedia.org/wiki/kvadratrix#mediaviewer/file:quadratrix_animation.gif
1 A kvadratrixról A kvadratrix más néven triszektrix nevű síkgörbéről az [ 1 ] és [ 2 ] munkákban is olvashatunk. A keletkezéséről készített animáció itt tekinthető meg: http://hu.wikipedia.org/wiki/kvadratrix#mediaviewer/file:quadratrix_animation.gif
További adalékok a merőleges axonometriához
 1 További adalékok a merőleges axonometriához Egy szép összefoglaló munkát [ 1 ] találtunk az interneten, melynek előző dolgoza - tunkhoz csatlakozó részeit itt dolgozzuk fel. Előző dolgozatunk címe: Kiegészítés
1 További adalékok a merőleges axonometriához Egy szép összefoglaló munkát [ 1 ] találtunk az interneten, melynek előző dolgoza - tunkhoz csatlakozó részeit itt dolgozzuk fel. Előző dolgozatunk címe: Kiegészítés
A Cassini - görbékről
 A Cassini - görbékről Giovanni Domenico Cassini, a 17-18 században élt olasz származású francia csillagász neve egyebek mellett a róla elnevezett görbékről is ismert lehet; ilyeneket mutat az 1 ábra is
A Cassini - görbékről Giovanni Domenico Cassini, a 17-18 században élt olasz származású francia csillagász neve egyebek mellett a róla elnevezett görbékről is ismert lehet; ilyeneket mutat az 1 ábra is
Keresztezett pálcák II.
 Keresztezett pálcák II Dolgozatunk I részéen a merőleges tengelyű pálcák esetét vizsgáltuk Most nézzük meg azt az esetet amikor a pálcák tengelyei nem merőlegesen keresztezik egymást Ehhez tekintsük az
Keresztezett pálcák II Dolgozatunk I részéen a merőleges tengelyű pálcák esetét vizsgáltuk Most nézzük meg azt az esetet amikor a pálcák tengelyei nem merőlegesen keresztezik egymást Ehhez tekintsük az
Trigonometria. Szögfüggvények alkalmazása derékszög háromszögekben. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1
 Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Trigonometria Szögfüggvények alkalmazása derékszög háromszögekben 1. Az ABC hegyesszög háromszögben BC = 14 cm, AC = 1 cm, a BCA szög nagysága
Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Trigonometria Szögfüggvények alkalmazása derékszög háromszögekben 1. Az ABC hegyesszög háromszögben BC = 14 cm, AC = 1 cm, a BCA szög nagysága
Fizika 1i, 2018 őszi félév, 4. gyakorlat
 Fizika 1i, 018 őszi félév, 4. gyakorlat Szükséges előismeretek: erőtörvények: rugóerő, gravitációs erő, közegellenállási erő, csúszási és tapadási súrlódás; kényszerfeltételek: kötél, állócsiga, mozgócsiga,
Fizika 1i, 018 őszi félév, 4. gyakorlat Szükséges előismeretek: erőtörvények: rugóerő, gravitációs erő, közegellenállási erő, csúszási és tapadási súrlódás; kényszerfeltételek: kötél, állócsiga, mozgócsiga,
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
