KŐZETCSAVAROK ERŐJÁTÉKÁNAK MEGHATÁROZÁSA A BIZTOSÍTÁS TERVEZÉSÉHEZ ÉS ELLENŐRZÉSÉHEZ SOMOSVÁRI ZS. - NÉMETH A.
|
|
|
- Fanni Kovács
- 8 évvel ezelőtt
- Látták:
Átírás
1 NME Közleményei, Miskolc, I. Sorozat, Bányászat, 34(1986) kötet, 1-4. füzet, KŐZETCSAVAROK ERŐJÁTÉKÁNAK MEGHATÁROZÁSA A BIZTOSÍTÁS TERVEZÉSÉHEZ ÉS ELLENŐRZÉSÉHEZ SOMOSVÁRI ZS. - NÉMETH A. összefoglalás: A tanulmány foglalkozik a kőzetcsavarozás tervezésének legalapvetőbb kérdéseivel. Levezeti folyamatosan rögzített súrlódásos és műgyantával ragasztott kőzethorgonyok erőjátékát próbaterhelés esetén. A levezetett eredményeket mészkőtestbe ragasztott csőhorgonyon végzett laboratóriumi mérésekkel ellenőrzi. A számított és mért eredmények jó egyezése alapján foglalkozik a kőzetcsavarok erőjátékával természeti körülmények között. Meghatározza pontrögzítésű és folyamatos rögzítésű kőzetcsavarok célszerű alkalmazásának körülményeit. Az üregbiztosítások klasszikus, az üregfelületet kívülről támasztó szerkezetei mellett helyet követelt magának a gyakorlatban egy olyan megoldás, amellyel a biztosítóelemeket a kőzetbe fúrt lyukakba erősítik és így érnek el biztosító hatást. Ezt a biztosítási módot kőzethorgonyzásnak, ill. kőzetcsavarozásnak nevezték el. A kőzetcsavaros biztosítás aztán különösen a II. világháború után nemcsak a szénbányászatban, hanem az alagútépítésben, mélyépítésben és különböző földművek rézsűinek védelmére széles körben elterjedt. Az 1940-es évektől kezdődően előbb az USA-ban az érc- és szénbányászatban egyaránt, majd Franciaországban az ércbányászatban alkalmazták tömegesen a mechanikus DR. SOMOSVÁRI ZSOLT oki. bányamérnök a műszaki tudomány kandidátusa NÉMETH ALAJOS oki. bányamérnök egyetemi adjunktus A kézirat beérkezett: fan. 8. Nehézipari Műszaki Egyetem Bányaműveléstani Tanszék Miskole-Egyetemváros 205
2 pontrögzítésű kőzetcsavarokat. Ezután alkalmazták a folyamatosan tögzített kőzetcsavarokat, előbb cementhabarcsos, majd műgyanta ragasztással. A nagyszilárdságú, gyorskötésű, gyorsan szilárduló, de drága műgyanták megjelenésével a pontrögzítésű műgyantával ragasztott kőzetcsavarok kezdtek inkább elterjedni Franciaországban, majd a kőzetcsavarozás a szénbányászatban is széles körben elterjedt nemcsak vágatokban, hanem fejtésekben is. Hazánkban az 1950-es évek végétől kezdődően üzemi kísérletek, elméleti és laboratóriumi kőzetcsavar vizsgálatok indultak a szén- és ércbányászatban egyaránt. Ennek ellenére a magyar szénbányászatban a kőzetcsavaros biztosítást jó néhány üzemi kísérlet ellenére önálló biztosításként tömegesen nem, csak kombinált biztosítás részeként alkalmazzák, önálló biztosításként csak az ércbányászat, főleg a mecseki ércbányászat alkalmazza tömegesen a kőzetcsavarozást. A kőzetcsavaros biztosítás nagyobb mértékű hazai elterjedésének alapvető korlátozó hatásait az alábbiak szerint lehet röviden összefoglalni: Hazánkban eddig nem sikerült megoldani a kőzetcsavarok beépítésének gépesítését még részben sem, ezért ez a biztosítás általában drágább, mint a hagyományos biztosítások. Külföldi tapasztalatok szerint egyedi beépítésnél a kőzetcsavaros biztosítás beépítési költségei (lyukfúrás, rögzítés stb...) általában nagyobbak a hagyományos biztosítás beépítési költségeinél, ezért a szerkezet olcsóbb volta ellenére végeredményben drágább a kőzetcsavaros biztosítás a hagyományosnál. A kőzetcsavaros biztosítás gépesítésével azonban megfordul ez a helyzet. Hazánkban még maga a tömeges lyukfúrás is sokszor nehézségeket okoz, amely eleve akadálya a kőzetcsavarozás elterjedésének. A MÉV üzemeiben, ahol a kőzetcsavarok beépítésének gépesítését részben megoldották (gépi előtolású fúrás), lényegesen olcsóbb a kőzetcsavarozás, mint a TH-biztosítás. A kőzetcsavarozás műszaki és gazdasági előnyei a hagyományos biztosítószerkezetekkel szemben elsősorban a nagyszelvényű bányavágatokban dominálóak. Hazánkban még kevésbé terjedtek el azok a technikák (pl. LHD), amelyek nagyszelvényű vágatokat kívánnak, így a vágatok általában kisebb szelvényűek, biztosításuk a hagyományos módon is megoldható. A kőzetcsavaros üregbiztosítás beépítése nagyobb technológiai fegyelmet kíván, mint a hagyományos biztosítások beépítése. A beépítés, jósága" vizuálisan nem, csak műszeres mérésekkel ellenőrizhető és az ellenőrzés nem maradhat el. Az üzemek ezért a sikeres kőzetcsavarkísérletek ellenére is idegenkednek e megoldás bevezetésétől. Az elvégzett kőzetcsavar kísérletek nem voltak mindig körültekintően megtervezettek, ezért sikertelen kísérletek is szép számmal születtek, amelyek nyilvánvalóan nem segítették elő az alkalmazás elterjesztését. A sikeres kísérletek pedig nem kaptak mindig publicitást. Tehát nem a kőzetcsavaros biztosítás, mint műszaki megoldás elégtelensége miatt nem terjedhetett el eléggé hazánkban ez a biztosítási mód, hanem a fentebb vázolt okok miatt. A másik oldalról viszont tudomásul kell venni azt, hogy a kőzetcsavarozás nem egy generális biztosítási mód, hanem csak ott alkalmazható önállóan sikerrel, ahol a biztosí- 206
3 tásigény (kn/m 2 ) nem túl nagy. Tekintettel arra, hogy egy-egy kőzet csavartól kn nagyságú kőzetfelületi biztosításreakciót várhatunk el, továbbá a beépítés sűrűsége gazdaságosan nem lehet nagyobb 1,5 db/m 2 -nél, ezért a maximálisan kifejthető kőzetfelületi biztosításreakció mintegy kn/m 2 = 0,075-0,150 MPa. Ennél nagyobb kívánalomnál a kőzetcsavaros biztosítás önálló biztosításként nem alkalmazható. A kőzetcsavaros biztosítás tehát elsősorban ott jön számításba, ahol a kőzetkörnyezet üregnyitás után a biztosítás hatására rugalmas állapotban marad, vagy biztosítás nélkül is rugalmas állapotú, csak önmagában nem kellő biztonsággal. A hazai szénbányászat gyengébb szilárdságú és változatos de korántsem különleges kőzetkörülményei kétségtelenül szűkebb teret engednek a kőzetcsavarozásnak, de a mai alkalmazásnál feltétlenül nagyobbak a lehetőségek. 1. A kőzetcsavarozás tervezésének alapvető kérdései Adott üregnél, adott kőzetkörülmények mellett először mindig az a kérdés vetődik fel, hogy a sokféle kőzetcsavar közül milyen típusú kőzetcsavart célszerű alkalmazni. Mechanikai viselkedés szerint az alábbi kőzetcsavar típusokat különböztetik meg: pontrögzítésű kőzetcsavarok, folyamatos rögzítésű kőzetcsavarok, kombinált rögzítésű kőzetcsavarok. Ezen típusok közül lehet a tervezéseknél választani. A pontrögzítésű kőzetcsavarok eredeti fajtái az ún. mechanikus csavarok, mint a feszítőékes, feszítőhüvelyes, gumihüvelyes kőzetcsavarok. Ma a pontragasztott kőzetcsavarokat kell a pontrögzítésű kőzetcsavarok közül a legfontosabbnak tekinteni. A ragasztás műgyantával vagy cementhabarcs csal történhet. A folyamatosan rögzített kőzetcsavarok eredeti fajtája a cementhabarccsal ragasztott kőzetcsavar, amelyet a műgyantával végig ragasztott kőzetcsavarok máig sem szorítottak ki. A folyamatosan rögzített kőzetcsavarok másik csoportjába a legújabb kőzetcsavarok, a Split-Set (hasított cső) és a Swellex (zömített cső) tartoznak, amelyeket súrlódásos kőzetcsavaroknak nevezhetünk. A kombinált kőzetcsavarok a pontrögzítésű és folyamatos rögzítésű kőzetcsavarok előnyös tulajdonságait egyesítik. Ilyen horgony pl. a Kiruna-horony, amelyet ékes fejrögzítés után cementhabarccsal végig ragasztanak, vagy az ún. exploziós horgony, amelynél a csőhorgony végét egy kis töltet elrobbantásával rögzítik, majd cementhabarccsal végigragasztják a horgonyt. Az alapvető biztosítószerkezeti tulajdonságok, aktivitás passzivitás, engedékenység merevség tekintetében különböznek egymástól a kőzetcsavarok. Aktív megtámasztást a pontrögzítésű és egyes kombinált rögzítésű kőzetcsavarok adnak, a folyamatosan rögzített kőzetcsavarok szigorúan véve passzív működésűek. Itt meg kell jegyeznünk, hogy ezeknek a kőzet csavaroknak a passzivitása korántsem olyan mértékű, mint a klasszikusan paszszív (pl. TH) biztosítószerkezeteké. A kőzetcsavaros biztosításnál szerves kapcsolatban van a biztosítás a kőzettel, itt a legteljesebb az együttdolgozás. A folyamatosan rögzített kőzetcsavarok a legkisebb kőzetexpanzióra aktivizálódnak éppen a szükséges mértékig. 207
4 Ezért a folyamatos rögzítésű kőzetcsavarokat kvázi-aktív biztosítószerkezetnek tekinthetjük. Engedékeny működésűek a folyamatosan rögzített súrlódásos kőzetcsavarok és egyes kombinált rögzítésű kőzet csavarok. A pontrögzítésű, a folyamatosan ragasztott és egyes kombinált rögzítésű kőzetcsavarok merev biztosítószerkezetek. Ahhoz, hogy a kőzetcsavarozás tervezésénél kiválaszthassuk az adott célra leginkább megfelelő kőzetcsavart az előbbieken kívül az egyes kőzetcsavartípusok erőjátékát kell ismernünk. 2. Folyamatosan rögzített súrlódásos kőzethorgonyok erőjátéka próbaterhelésnél A horgony kőzetfelületből kiálló végének húzóerővel való terhelésekor a horgony x helyen lévő keresztmetszeteiben (x = 0 hely a kőzetfelület) húzóerők ébrednek. Ezek a húzóerők a horgony szár rugalmas állapotának feltételezésével: P(x)=AE a eo)<pomax ahol: A - a horgony keresztmetszete, E a a horgony acélanyagának rugalmassági modulusa, e(x) - a horgony megnyúlása az x helyen. A horgonyban ébredő P(x) húzóerő az alábbiak szerint is kifejezhető: P(x) = í\x = 0) - f s(x)dx < P 0i ahol s(x) a horgony és a kőzet között ébredő egységnyi hosszra jutó súrlódóerő [s(x) = ds(x)ldx, kn/m]. A két egyenlet összevetéséből és differenciálásából de(x) dp(x) s(x) = -AE a < s max, s(x) = <s max. dx dx Abban az esetben, ha olyan húzóerőt működtetünk a csavarvégen, amely kihúzza a lyukból a kőzetcsavart, akkor egészen biztos, hogy végig igénybevételt szenved a kőzethorgony, a horgony mentén a fajlagos súrlódóerő a lehető legnagyobb és nem változik, azaz ilyenkor s \ x ), dx s max r L P(x)=P 0i jl 208
5 , v Pomax, (\x) = 1 AE a { L Amikor még P 0 nem éri el Po max értékét, azaz a kőzethorgony nem húzódik ki a fúrólyukból, akkor az erők megoszlása nem ilyen, de ha P 0 megközelíti Po max értékét, akkor jó közelítéssel számolhatunk a fenti erőeloszlással, azaz 1-y s{x) = -~, Po^Po, Abban az esetben viszont, ha P 0 < Po max > akkor egészen mások a viszonyok, hiszen a kőzethorgony igénybevétele nem is terjed ki a horgony egész hosszáig, hanem csak x 0 <L helyig. Kis húzóerőknél (P 0 -^ Po max) feltételezhetjük, hogy Másrészről ds(x) = C = const, Qm -1 ]. dp(*) <x) =. ax A két differenciálegyenlet összevetéséből ds{x) dx = Cs(x) ; s(x) = s 0 exp ( - Cx). azaz a fajlagos aktivizálódott súrlódóerő a horgonyszár mentén exponenciálisan csökken. A horgonyban ébredő erő: P(;c)=Po ^-[l-exp(-cx)] x = -nél P = 0 kell legyen, így C = s 0 /P 0. Ezzel P(x) =P 0 exp --p-x S(A:) = s 0 exp So Po x 209
6 e(x) = exp JC AE a y \ P 0 Az s 0 paraméter meghatározása érdekében képezzük a de{x) dx So AE a exp s 0 de(x) dx JC = 0 s AE n függvényeket. Innen s 0 = AE a de{x) dx x = 0 Az x = 0 helyen kialakuló megnyúlás változás független a P 0 húzóerőtől, ezért különböző Po "^ Pomax húzóerők alkalmazásakor s 0 = const, értékkel számolhatunk. A kőzetcsavarzár a kőzetfelülettől befelé haladva addig tekinthető aktivizálódottnak, ameddig megnyúlás jön létre benne, ill. ameddig súrlódóerő aktivizálódik a hossz mentén. Ha s = 0,05 s 0 fajlagos súrlódóerőtmár elhanyagolhatónak tekintjük akkor az aktivizálódott csavarhossz XQ = 3 So <L. Po = SQL azt a húzóerőt adja, amely működtetésénél az aktivizálódott csavarhossz éppen a kőzetcsavar beépített hosszával egyezik meg. Fenti számításunk P 0 < P' 0 húzóerők esetén érvényesek. Tekintettel arra, hogy a kőzetcsavar végén x = L helyen e = 0, P = 0, ezért Pönal nagyobb P 0 húzóerő létesítésekor a kőzetfelület közelében a 0 < x < JC intervallumban s(x) = s 0 = const, melletti viszonyok alakulnak ki, és a jelzett intervallumban nem érvényesül ds/dp = s 0 = const, kapcsolat. Ebben az intervallumban határigénybevétel éri a súrlódásos kapcsolatot és ezért P(x) lineárisan csökken. Az x távolság abból a feltételből határozható meg, hogy az állandó fajlagos súrlódóerő és a változó fajlagos súrlódóerő melletti kőzetcsavar szakaszok összege a horgonyhosszal egyenlő és x = L helyen P = 0. így 3P(x) [ Pomax - x L, másrészről P(x) =PQ\1 x LPo Ezért x = L 3Po ~>POma s 0 L
7 Amikor P 0 = Pomax> akkor x =La kőzetcsavar kicsúszik a fúrólyukból.p 0 <PÓműködtetésekor tehát a 0 < x < x intervallumban s(x) = s 0 = const., P(x) =P 0 11 = x LPQ az x < x < L intervallumban í Po - 1 s(x) = s 0 exp I (x x) I L So J 3Po _ i > W=/, omax o 1 - s 0 2/> ( omax -1 S 0 exp I (x x) I Az x = x helyen a csavarerőt leíró görbén akkor nincs törés, akkor folyamatos a görbe, ha Omax S 0 = - Ezt a feltételt elfogadhatjuk s 0 meghatározására, annál is inkább, mivel így So kísérlettel is viszonylag könnyen meghatározható. Ezzel 2 ^ Pomax ' így a 0< x <xintervallumbanp(x) =P 0 s 0 x, azx<x<l intervallumban i>(x) = 0,5(/»omax ~^o) exp - ["íh Ezek után végigkövethető, hogy egy súrlódásos horgony kíréleti terhelése közben hogyan alakul a csavarerő, megnyúlás és fajlagos súrlódóerő. L = 2m hosszú súrlódásos kőzethorgony alapul vételével /omax = 80 kn kihúzódást okozó húzóerő mellett az erőviszonyok a kőzethorgonynál az 1. ábra szerint alakulnak. Az ábra mutatja, hogy kis húzóerők alkalmazásakor {PQ = kn) a horgonyszár nincs teljes hosszában igénybe véve, a csavarerő és a fajlagos súrlódóerő a csavarszár mentén exponenciálisan, egyre lassabban csökken. Nagyobb húzóerők alkalmazásakor (P 0 = kn) a kőzetcsavar első szakaszán a súrlódásos kapcsolat szempontjából határigénybevétel lép fel, a fajlagos súrlódóerő állandó, a csavarerő lineárisan csökken. A kőzetcsavar hátsó szakaszán még nincs a súrlódásos kapcsolat szempontjából határigénybevégetel. Itt a fajlagos súrlódóerő exponenciálisan és lassabban csökken. Még nagyobb húzóé rőkalkalmazásakor (P 0 = kn), csaknem a kőzetcsavar teljes hosszán határigénybevétel lép fel a súrlódásos kapcsolat szempontjából. MigP = 0 A>max = 211
8 to P[kN] x[m] 0,2 QU Q6 0, ,2 U tt ábra. Folyamatosan rögzített súrlódásos kőzethorgony erőjátéka próbaterhelésnél 2J0 x [mj
9 = 80 kn húzóerő alkalmazásakor a kőzetcsavar teljes hossza mentén határigénybevétel lép fel a súrlódásos kapcsolat szempontjából, a kőzetcsavar kihúzódik a fúrólyukból. Az 1. ábra mutatja, hogy a határigénybevételt megközelítő terhelésnél a kőzetcsavarerő a P{x)=P Q \l-~ összefüggéssel csak akkor közelíthető jól, ha 0,9 <P 0 </omax- Az ábra egyben a e(x) diagramot is adja tekintettel az e(x) = P(x)jAE a kapcsolatra. Hosszú kó'zethorgonyok esetében a terhelő húzóerő növekedésével a kőzethorgony elején előbb bekövetkezhet a súrlódás szempontjábóli hatáigénybevétel, minthogy a kőzetcsavar egész hosszában aktivizálódna. Ilyenkor a csavarerők eloszlásának 1. ábrán vázolt képe csak annyit változik, hogy a csavarerők lefutásának lineáris tartományai megnövekednek. 3. Műgyanta ragasztóval folyamatosan rögzített horgonyok erőjátéka próbaterhelésnél A műanyag ragasztóval folyamatosan rögzített kőzethorgonyok erőjátéka teljesen analóg tárgyalható a súrlódásos végigrögzített kőzethorgonyok erőjátékával, hiszen a kőzetcsavar szárát csak 2 3 mm vastag műanyag ragasztó hártya választja el a fúrólyuk falától, így a csavarszár alakváltozása teljes mértékben átadódik: a ragasztóhártyának, a ragasztóhártya pedig tapadás, adhézió révén rögzíti a csavarszárat. A fajlagos súrlódó erő helyett itt fajlagos tapadó erővel kell számolni. A horgony végének húzóerővel való terhelésekor: P(x)=AEa e(x)iü. P(x) =P 0 - J" t(x)dx<p 0l X dp(x) t(x) = - < r max dx ahol t{x) a fúrólyuk fala és a ragasztás között ébredő fejlagos szárirányú tapadóerő. Továbbá feltételezzük a dt(x) = C = const. kapcsolat. így dt(x) dx = Ct(x), t(x) = t 0 exp ( Cx) 213
10 Ezzel P(x) =Po- [1 ~ exp (- Cx)] x = -nél P = 0, ezért C = í 0 \P 0. így P{x) = PQ exp ío f(x) = í 0 exp - x\, e(x) = exp - x P 0 I Aß a l "o = P(x) Továbbá de(x) í 0 f f 0 I de(x) = exp x, dx AE a \ Po ) dx tp x=0 AE a Innen í 0 =~AE a de(x) dx ill. ío = - P(x) e(x) de(x) dx x = 0 - const. Az átlagos aktivizálódott fajlagos tapadás (í) és í 0 értéke között az alábbi összefüggés áll fenn: 1 X fp = J' t(x) x 0 J - Po í = xo exp dx ío, I A) ^omax jc 0-1 1= = Po ) -I xo L ahol x 0 az aktivizálódott csavarhosszat jelöli. í = 0,05 í 0 érték elhanyagolásánál Xo =3 "omax ío ezzel í = ill. í 0 = 3í = 3 L A Pomax terhelési kísérlettel meghatározható, így f 0 értékét kísérletek eredményeiből kapjuk. A fentiek igazolása, ül. ellenőrzése érdekében laboratóriumi kísérleteket végeztünk el a Bányamuvelsétani Tanszék kőzetmechanikai laboratóriumában. Az első kísérlet célja az volt, hogy próbaterhelés közben megmérjük a kőzetcsavarszár megnyúlását ill. meghatározzuk különböző Po terheléseknél a e(x) függvényt. Ennek érdekében méretezés alapján 214
11 d = 43 mm külső átmérőjű, v = 2 mm falvastagságú. A =25,5 cm 2 keresztmetszetű acélcsövet ragasztottunk mészkőtömbbe fúrt 45 mm átmérőjű, 200 mm hosszú fúrólyukba. Az acélcsövet anyagminőségének pontos megállapítására előbb szakítóviszgálatnak vetettük alá. Az anyag folyáshatára o a f = 583 MPa-nak adódott. A ragasztást kétkomponensű epoxi műgyantával végeztük. Előzetesen elvégzett 56 db ragasztási kísérletünk eredményei szerint ez a műgyantat max = 7,2-8,8 MPa maximális átlagos tapadást tud produkálni laboratóriumi körülmények között. A beragasztott acélcső belsejébe tengelyirányban egymással szemben 4 4 helyen összesen 8 db KYOWA gyártmányú nyúlásmérőbélyeget ragasztottunk fel. A nyúlásmérőbélyeg-párok a 2. ábra szerint 50 mm-re helyezkednek el egymástól. A nyúlásmérőbélyegek elektromos jelét Hottinger Baldwin gyártmányú automata mérohíd segítségével mértük. A 200 mm hosszon beragasztott kőzetcsavar mérési helyein a terhelésalakváltozás görbék a 3. ábra szerint alakultak. Az ábra alapján megrajzolhatók különböző terheléseknél az e(x) görbék, amelyeket a 4. ábrán látunk. Az ábra mutatja, hogy a görbék kezdeti érintői egymással párhuzamosak, azaz de(x) = const. dx x=0 Az ábráról leolvasható, hogy ennek a constansnak az értéke 0,0131 m" 1.Továbbá AE a = = Pole 0 =( ) 10 3 kn, így t 0 = 2000 kn/m = 2 kn/mm. A számított megnyúlások: e(x) = exp 140 * 10 3 A x[mm] P 0 [kn] A számított megnyúlásokat az 5. ábrán látjuk. Az ábra képe csaknem tökéletesen megegyezik a 4. ábra képével. Ez azt jelenti, hogy feltevéseink helyesek voltak és a levezetett összefüggések alkalmasak az erőjáték leírására. A kísérletből meghatározhatjuk az aktivizálódott legnagyobb átlagos tapadás értékét is. 130 kn alkalmazott húzóerőmaximum és 0,028 m 2 ragasztott kőzetfelület figyelembevételével T = 4, 6 MPa-ra adódik. Tekintettel arra, hogy a 4. ábra diagramja azt mutatja, hogy még P 0 = 130 kn terhelésnél sem kezdődik meg a ragasztás, vagy a kőzet tönkremenetele, ezért ragasztásra jellemző r max > 4,6 MPa. A t 0 = 2 kn/mm = 2 MN/m, x = 0 helyen aktivizálódott fajlagos tapadáshoz tartozó r 0 tapadási érték 0,141 m ragasztott kőzetkerület figyelembevételével 14,2 MPa-ra adódna. A kőzethorgony próbaterhelésénél azonban a fúrólyuk szájának (x = 0 hely) közelében a kőzetnek is módja van deformálódni, követni a ragasztó deformációját, így itt feltétlenül kisebb az aktivizálódott tapadás a számítottnál. Az a maximális terhelőerő, amely a ragasztás adhéziójának megszűnését idézi elő, Pomax =140 kn-ra tehető. Ezzel és L = 200 mm ragasztási hossz figyelembevételével a 215
12 ábra. Ragasztott csőhorgony és mérőbélyegek mészkőtömbben laboratóriumi kísérletnél
13 to 1 > -J 0,1 Q2 Q3 Q4 Q5 0,6 0,7 3. ábra. Próbaterhelés mért terhelés-alakváltozás görbéi a mérőbélyegek helyein í [%oj
14 h ' x [mm] (T) mérőbélyeg sorszáma 4. ábra. A mért terhelés-alaváltozás görbék alapján meghatározott alakváltozás lefutás a ragasztott csőhorgonyban
15 ! mérőbélyeg 200 xcrnmj sorszáma to > * 5. ábra. Számított alakváltozás lefutása a esohorgonyban
16 t 0 =3Po max /L képletből r 0 2,1 kn/mm-re adódik. Ez az eredmény a mérési eredményekhez képest mindössze 5%-os eltérést mutat. Egy másik hasonló kísérlettel arról kívántunk meggyőződni, hogy egy kőzeteiválási felület hogyan befolyásolja a deformáció, ill. erőeloszlást. Ennek érdekében a kísérletnél felhasznált mészkőtömböt a fúrólyukra merőleges síkban kettévágtunk és az elválási felülettel rendelkező mészkőtömbbe ragasztottuk be az előbbi kísérlethez hasonlóan az acélcsövet, összesen 8 db nyúlásmérő bélyeggel a 6. ábra szerinti elrendezésben. Itt rosszabb minőségű ragasztást produkáltunk annak érdekében, hogy a ragasztás tönkremenetelének kezdetét is ki tudjuk mutatni. A 200 mm hosszon beragasztott kőzetcsavar mérési helyein a terhelés-alakváltozás görbék a 7. ábra szerint alakultak. Ezen ábra alapján megrajzolt e(x) görbéket a 8. ábra mutatja. Látható, hogy az elválási felület mentén ugrás van a kőzethorgony megnyúlásában, az elválási felület két szakaszra osztja a deformáció-eloszlást. A P 0 = 20, 40, 60, 80 kn húzóerőhöz tartozó e(x) görbék kezdeti érintői egymással párhuzamosak [de(x)ldx]o =sx = 0,0078. Ez az érték csak 60%-a az előbbi kísérletnél kapott értéknek, a megnyúlás és a csavarerő tehát x növekedésével lassabban csökken, azaz kisebb fajlagos tapadó erő aktivizálódik az I. szakaszon. Ennek oka egyrészt az elválási felület jelenléte, amely ugrást enged meg a kőzetcsavar megnyúlásában, másrészt a rosszabb ragasztás. A JPO = 100 kn terhelésnél lényegesen kisebb az e(x) görbe kezdeti érintőjének irányszöge és a megnyúlás csökkenése már lineárisnak tekinthető. Ez annak a jele, hogy ennél a terhelésnél a ragasztó a kőzetfelületen elkezd tönkremenni és az adhéziós kapcsolat helyett súrlódásos kapcsolat érvényesül. Ezért ebben az esetben ilyen terhelésnél már nem érvényes a dt{x)\dp{x) = C kapcsolat. A ragasztás tönkremenetele az I. szakaszon P 0 = 100 kn terhelésnél azért következik be, mert az elválási felület kettéosztja a ragasztott felületet és az első szakaszon 50% erőt kellene felvennie a ragasztásnak, miközben a ragasztott felület 38%-ra csökken. így az II. szakasz túlterhelése 1,32-szeres az elválási felület nélküli esethez képest. Ehhez jön még, hogy a ragasztás minősége ennél a kísérletnél rosszabb mint az előzőnél. A kőzetcsavar P 0 = 100 kn terhelésnél még nem húzódik ki annak ellenére, hogy az I. szakaszon már csak súrlódásos kapcsolat érvényesül a ragasztó és kőzet között. Ezen a szakaszon csak 26 kn-t csökken a csavarerő, a ragasztás ennyi erőt vesz fel. Az elválási felület után a II szakasz elején 50 kn erő ébred a kőzetcsavarban, amelyet a ragasztás ezen a szakaszon felvesz. Az elválási felületnél 24 kn-t csökken a kőzetcsavarerő, mert a az elválási felületen a kőzetfelületek közeledésére van szükség. A végén megterhelt kőzetcsavar a két kőzettömböt egymáshoz húzza. Az elvégzett laboratóriumi kísérletek eredményei igen jól alátámasztják a levezetett összefüggéseket. Az elvégzett vizsgálatok alkalmasak arra is, hogy segítségükkel természeti körülmények között tárgyaljuk a kőzetcsavarok erőjátékát. 4. Kőzetcsavarok erőjátéka természeti körülmények között A pontrögzítésű (pontragasztott) kőzetcsavarok erőjátéka természeti körülmények között is hasonlóan alakul mint próbaterhelés alkalmával. Ezért nem foglalkoztunk külön 220
17 6. ábra. Ragasztott csőhorgony és mérőbélyegek elválási felülettel rendelkező mészkőtömbben laboratóriumi kísérletnél
18 to to to [kn] inn - rp> (o\ ft ST\ fln r i i 0 H 0 1 0, k 0,5 0,6 Q 7 0,8 0,9 6 [% ] 7. ű'ftra. Próbaterhelés mért terhelés-alakváltozás görbéi a mérőbélyegek helyein
19 I. szakasz II. szakasz 26kN %, 24kN 50kN 200 x [mm] merobelyegek sorszama to - 8. ábra. A mért terhelés-alakváltozás görbék alapján meghatározott alakváltozás lefutás a ragasztott esohorgonyban
20 ^tf á r^4t%% #^ÉMf t s o ö Rí :* v 8 5 SDJ9Z OJdJOAOSD fzz&zzzzzzz^zzzazzzz f>///77//^///f>///77/// 77;lh, v^x//yyx/y//-aiw##/«^r///x/////////////«#//#/////// 0 c SJ *5 11 :0,X»3 a> 0) v\, *<u >1) >,Í.J >> " * C <-. SP <A V s S3 o > E a o tu is N *o u_ ü, 224
21 a 225
22 a pontrögzítésű kőzetcsavarok erőjátékával próbaterhelésnél. A pontragasztott kőzetcsavar beépített hossza ragasztott (/ r ) hosszból és szabad szárhosszból (/ 0 ) áll. Beépítés és előfeszítés után, majd csavarszárirányú kőzetexpanzió hatására a szabad szárhossz mentén a csavarszár megnyúlásával (e a ) arányos, állandó nagyságú P = E a e a = P e + AP húzóerő ébred, ahol P e az előfeszítés hatására, AP az expanzió hatására ébredő erő. Ha a kőzetexpanzió hatására A/ mértékű az A keresztmetszetű kőzetcsavar szár megnyúlása, a kőzetfelület szárirányú elmozdulása, akkor A/ AP = E a A k Adott A/ elmozdulásnál minél nagyobb a szabad szárhossz (/ 0 ) annál kisebb mértékű az elmozdulás miatti aktivizálódás. Ha az / 0 hosszon belül heterogén kőzetrétegek helyezkednek el, akkor a puhább rétegek összenyomódásának rovására is bekövetkezik rétegszétválás, amelyre a kőzetcsavar nem aktivizálódik. Tehát olyan esetben, amikor hoszszabb kőzetcsavarokra van szükség, vagy heterogén felépítésű az áttűzött rétegsor, a pontrögzítésű kőzetcsavarok rétegelválásnál kevésbé aktivizálódnak. A szóban forgó erők és megnyúlások próbaterheléssel reprodukálhatók, ezért a pontrögzítésű kőzetcsavarok próbaterhelésnél kapott eredmények az,,in situ" viszonyokat jellemzik. Nem így van ez folyamatosan rögzített kőzetcsavarok esetében. A folyamatosan rögzített (ragasztott vagy súrlódásos) kozetcsavarok beépítéskor nem vesznek magukra terhelést csak az alátétlemezzel ellátott csavarvég feszül meg rövid szakaszon. Ezt mutatja a 9. ábra. A folyamatosan rögzített kőzetcsavar a kőzetkörnyezet csavarszár irányú expanziójának hatására aktivizálódik. A kőzetexpanzió az elválási felületek távolodásával megy végbe, az elválási felületeknél a csavarszár Ali APi = - E a A mértékben aktivizálódik és éppen ott, ahol erre szükség van. Minél több a szétnyíló elválási felület, annál inkább kihasználttá válik a csavarszár. Ezt látjuk a 10. ábrán. Folyamatos rögzítésű kőzetcsavaroknál is célszerű l r rögzítési hosszat és / 0 szárhosszat megkülönböztetni. Ugyanis akkor akadályozza a folyamatos rögzítésű kőzetcsavar a kőzetexpanziót a legintenzívebben, ha az l r rögzítési hossz olyan helyen van, ahol már rétegelválás nincs. Az aktivizálódás mértéke folyamatosan rögzített kőzetcsavarnál lényegesen nagyobb, mint pontrögzítésű kőzetcsavarok esetében, mert A/ 0 < l 0. A folyamatos rögzítésű kőzetcsavarok tehát heterogén kőzetkörnyezetben aktivizálódnak jobban, a kőzetcsavar hossza nem korlátja az aktivizálódásnak. 5. Megállapítások A fentiekből következik, hogy heterogén kőzetkörnyezetben a folyamatos rögzítésű (ragasztott és súrlódásos), homogén kőzetkörnyezetben kisebb kőzetcsavarhosszúságok- 226
23 nál a pontrögzítésű (pontragasztott) kőzetcsavarok használhatók előnyösebben. Homogén kőzetkörnyezetben, de nagyobb hosszúságigényű kőzetcsavarozásnál megint csak a folyamatos rögzítésű kőzetcsavarok alkalmazását kell előtérbe helyeznünk. Folyamatos rögzítésű kőzetcsavaroknál a kőzetcsavar in situ" terhelésű erőjáréka lényegesen eltér a helyszínen végzett próbaterhelés hatására előálló erőjátéktól. Egy ragasztott kőzetcsavar akkor is eleget tehet a próbaterhelés követelményeinek (pl. viseljen el 50 kn húzóerőt), ha csak részben van a csavarszár akár elől, akár hátul beragasztva. Ugyanez áll a súrlódásos kőzetcsavaroknál is. Tehát a folyamatosan rögzített kőzetcsavarok próbaterhelésének eredményeit korántsem szabad úgy kezelnünk, mint a pontrögzítésű kőzetcsavarok próbaterheléseinek eredményeit. Ragasztott kőzetcsavarok próbaterhelésnél kapott általában nagy, a csavarszárat elszakító húzóerők csak viszonylagosan jellemzik a kőzetcsavar rögzítettségét és működőképességét. A hazai szénbányászat heterogén, kisszilárdságú kőzetkörnyezete általában folyamatos rögzítésű kőzetcsavarok alkalmazását teszi célszerűvé. A kisebb kőzetszilárdság hosszabb kőzetcsavarok alkalmazását kívánja. A legújabban megjelent csőhorgonyok (Split-Set, Swellex) engedékenysége igen előnyös biztosítószerkezeti tulajdonság, különösen kisebb kőzetszilárdság esetén. Mindezek miatt azt kell mondanunk, hogy a folyamatosan rögzített súrlódásos kőzethorgonyok várhatóan új lökést adnak a kőzetcsavarozás alkalmazásának hazánkban. IRODALOM 1. Bányaműveléstani Tanszék:^ kőzetcsavarozás elméleti és gyakorlati kérdéseinek vizsgálata. Kutatási részjelentés, Bányaműveléstani Tanszék: Kőzethorgonyok erőjátéka és méretezése, a fejtési üregek stabilitásának vizsgálata (I). Laboratóriumi és üzemi kísérletek eredményei (II). Kutatási részjelentés, PENG, S. S.: Coal Mine Ground Control. Wiley Interscience Publication, New York, SOMOSVÁRI ZS.-.A kőzethorgonyos üregbiztosítás mechanikai jellemzőt (Könyvrészlet). Hansági, I.: Gyakorlati kőzetmechanika az ércbányászatban. Műszaki Könyvkiadó (Megjelenés alatt). DETERMINATION OF FORCES IN ROCK BOLTS IN DESIGN AND CONTROL OF SUPPORT by ZS. SOMOSVÁRI - A. NÉMETH Summary The study looks into the basic problems of rock bolt design. The forces are analysed for continuously fixed frictional and resin-glued rock anchors under experimental load. The theoretical results are checked by laboratory measurements on a tube anchor glued to a limestone body. Calculated and measured results agree very well. The study also determines the forces in rock bolts under natural circumstances and the suitable fields of application for point-fixed and continuously fixed rock bolts. 227
24 BESTIMMUNG DER KRÄFTE IN GESTEINSSCHRAUBEN ZUR AUSLEGUNG UND KONTROLLE DES AUSBAUES von ZS.SOMOSVÄRI - A.NÉMETH Zusammenfassung Die grundsätzlichen Fragen der Auslegung der Gesteinsverschraubung sind im Aufsatz dargelegt. Die Kräfte in den kontinuierlich befestigten Reibungs- und kunstharzgeklebten Gesteinsschrauben sind für Probenbelastung abgeleitet. Die abgeleiteten Ergebnisse wurden durch Labormessungen an einer in einem Kalksteinblock geklebten Gesteinsschraube kontrolliert. Aufgrund der guten Übereinstimmung der berechneten und gemessenen Ergebnisse werden die Kräfte der Gesteinsschrauben unter natürlichen Bedingungen analysiert. Die zweckmäßigen Anwendungsbedingungen der punktbefestigten und der kontinuierlich befestigten Gesteinsschrauben werden erörtert. ОПРЕДЕЛЕНИЕ СИЛ В ПОРОДНЫХ БОЛТАХ ДЛЯ ПРОЕКТИРОВАНИЯ И КОНТРОЛЯ КРЕПИ Ж. ШОМОШВАРИ - А. НЕМЕТ Резюме В работе рассматриваются основные вопросы анкерного крепления. Приводится вывод сил в непрерывно-фиксированного фрикционного и скленного синтетической смолой анкерах в случае пробной нагрузки. Полученные результаты были проверены в лабораторных условиях на трубчатом анкере, вклеенном в известняковое тело- На основе хорошей сходимости расчетных и эесп ери ментальных данных в работе рассматриваются силы в породных болтах в природных условиях. Определены условия целесообразного применения точечно-фиксированных и непрерывно-фиксированных породных болтов. 228
ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS
 Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Alagútfalazat véges elemes vizsgálata
 Magyar Alagútépítő Egyesület BME Geotechnikai Tanszéke Alagútfalazat véges elemes vizsgálata Czap Zoltán mestertanár BME Geotechnikai Tanszék Programok alagutak méretezéséhez 1 UDEC 2D program, diszkrét
Magyar Alagútépítő Egyesület BME Geotechnikai Tanszéke Alagútfalazat véges elemes vizsgálata Czap Zoltán mestertanár BME Geotechnikai Tanszék Programok alagutak méretezéséhez 1 UDEC 2D program, diszkrét
Szádfal szerkezet ellenőrzés Adatbev.
 Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
Akusztikus aktivitás AE vizsgálatoknál
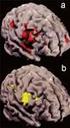 Akusztikus aktivitás AE vizsgálatoknál Kindlein Melinda, Fodor Olivér ÁEF Anyagvizsgáló Laboratórium Kft. 1112. Bp. Budaörsi út 45. Az akusztikus emissziós vizsgálat a roncsolásmentes vizsgálati módszerek
Akusztikus aktivitás AE vizsgálatoknál Kindlein Melinda, Fodor Olivér ÁEF Anyagvizsgáló Laboratórium Kft. 1112. Bp. Budaörsi út 45. Az akusztikus emissziós vizsgálat a roncsolásmentes vizsgálati módszerek
Cölöpcsoport elmozdulásai és méretezése
 18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Fogorvosi anyagtan fizikai alapjai 6.
 Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
A.2. Acélszerkezetek határállapotai
 A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
KÖTÉSEK FELADATA, HATÁSMÓDJA. CSAVARKÖTÉS (Vázlat)
 KÖTÉSEK FELADATA, HATÁSMÓDJA. CSAVARKÖTÉS (Vázlat) Kötések FUNKCIÓJA: Erő vagy nyomaték vezetése relatív nyugalomban lévő szerkezeti elemek között. OSZTÁLYOZÁSUK: Fizikai hatáselv szerint: Erővel záró
KÖTÉSEK FELADATA, HATÁSMÓDJA. CSAVARKÖTÉS (Vázlat) Kötések FUNKCIÓJA: Erő vagy nyomaték vezetése relatív nyugalomban lévő szerkezeti elemek között. OSZTÁLYOZÁSUK: Fizikai hatáselv szerint: Erővel záró
Frissítve: Csavarás. 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat.
 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk
1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA
 FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
Cölöpalapozások - bemutató
 12. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpalapozások - bemutató Ennek a mérnöki kézikönyvnek célja, hogy bemutassa a GEO 5 cölöpalapozás számításra használható programjainak gyakorlati
12. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpalapozások - bemutató Ennek a mérnöki kézikönyvnek célja, hogy bemutassa a GEO 5 cölöpalapozás számításra használható programjainak gyakorlati
Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1.
![Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1.](/thumbs/27/12197964.jpg) 1 Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Feladat Egy G gépkocsi állandó v 0 nagyságú sebességgel egyenes úton
1 Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Feladat Egy G gépkocsi állandó v 0 nagyságú sebességgel egyenes úton
Toronymerevítık mechanikai szempontból
 Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Egy nyíllövéses feladat
 1 Egy nyíllövéses feladat Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. 1. ábra forrása: [ 1 / 1 ] Igencsak tanulságos, ezért részletesen bemutatjuk a megoldását. A feladat Egy sportíjjal nyilat
1 Egy nyíllövéses feladat Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. 1. ábra forrása: [ 1 / 1 ] Igencsak tanulságos, ezért részletesen bemutatjuk a megoldását. A feladat Egy sportíjjal nyilat
Szilárd testek rugalmassága
 Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Rugalmasan ágyazott gerenda. Szép János
 Rugalmasan ágyazott gerenda vizsgálata AXIS VM programmal Szép János 2013.10.14. LEMEZALAP TERVEZÉS 1. Bevezetés 2. Lemezalap tervezés 3. AXIS Program ismertetés 4. Példa LEMEZALAPOZÁS Alkalmazás módjai
Rugalmasan ágyazott gerenda vizsgálata AXIS VM programmal Szép János 2013.10.14. LEMEZALAP TERVEZÉS 1. Bevezetés 2. Lemezalap tervezés 3. AXIS Program ismertetés 4. Példa LEMEZALAPOZÁS Alkalmazás módjai
6. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései
 Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései VII. Városi Villamos Vasúti Pálya Napra Budapest, 2014. április 17. Major Zoltán egyetemi tanársegéd Széchenyi István Egyetem, Győr
Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései VII. Városi Villamos Vasúti Pálya Napra Budapest, 2014. április 17. Major Zoltán egyetemi tanársegéd Széchenyi István Egyetem, Győr
Járműelemek. Rugók. 1 / 27 Fólia
 Rugók 1 / 27 Fólia 1. Rugók funkciója A rugók a gépeknek és szerkezeteknek olyan különleges elemei, amelyek nagy (ill. korlátozott) alakváltozás létrehozására alkalmasak. Az alakváltozás, szemben más szerkezeti
Rugók 1 / 27 Fólia 1. Rugók funkciója A rugók a gépeknek és szerkezeteknek olyan különleges elemei, amelyek nagy (ill. korlátozott) alakváltozás létrehozására alkalmasak. Az alakváltozás, szemben más szerkezeti
Leggyakoribb fa rácsos tartó kialakítások
 Fa rácsostartók vizsgálata 1. Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék Leggakoribb fa rácsos tartó kialakítások Változó magasságú Állandó magasságú Kis mértékben változó magasságú
Fa rácsostartók vizsgálata 1. Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék Leggakoribb fa rácsos tartó kialakítások Változó magasságú Állandó magasságú Kis mértékben változó magasságú
A beton kúszása és ernyedése
 A beton kúszása és ernyedése A kúszás és ernyedés reológiai fogalmak. A reológia görög eredetű szó, és ebben az értelmezésben az anyagoknak az idő folyamán lejátszódó változásait vizsgáló műszaki tudományág
A beton kúszása és ernyedése A kúszás és ernyedés reológiai fogalmak. A reológia görög eredetű szó, és ebben az értelmezésben az anyagoknak az idő folyamán lejátszódó változásait vizsgáló műszaki tudományág
Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése
 Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése Tóth László, Rózsahegyi Péter Bay Zoltán Alkalmazott Kutatási Közalapítvány Logisztikai és Gyártástechnikai Intézet Bevezetés A mérnöki
Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése Tóth László, Rózsahegyi Péter Bay Zoltán Alkalmazott Kutatási Közalapítvány Logisztikai és Gyártástechnikai Intézet Bevezetés A mérnöki
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS!
 Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I. rész
 Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
HÍDKONFERENCIA 2019 GERENDA VÁLASZTÁS FA-BETON ÖSZVÉRTARTÓKHOZ
 HÍDKONFERENCIA 2019 GERENDA VÁLASZTÁS FA-BETON ÖSZVÉRTARTÓKHOZ Kedvcsináló 2018. évi előadás summája a nyugattól való 20-30 éves a lemaradás után, a felzárkózás szükségszerűsége; az előnyök és hátrányok
HÍDKONFERENCIA 2019 GERENDA VÁLASZTÁS FA-BETON ÖSZVÉRTARTÓKHOZ Kedvcsináló 2018. évi előadás summája a nyugattól való 20-30 éves a lemaradás után, a felzárkózás szükségszerűsége; az előnyök és hátrányok
Méréselmélet és mérőrendszerek
 Méréselmélet és mérőrendszerek 6. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba eredete o
Méréselmélet és mérőrendszerek 6. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba eredete o
Szádfal szerkezet tervezés Adatbev.
 Szádfal szerkezet tervezés Adatbev. Projekt Dátum : 0..005 Beállítások (bevitel az aktuális feladathoz) Nyomás számítás Aktív földnyomás számítás : Passzív földnyomás számítás : Földrengés számítás : Ellenőrzési
Szádfal szerkezet tervezés Adatbev. Projekt Dátum : 0..005 Beállítások (bevitel az aktuális feladathoz) Nyomás számítás Aktív földnyomás számítás : Passzív földnyomás számítás : Földrengés számítás : Ellenőrzési
Ejtési teszt modellezése a tervezés fázisában
 Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Síklapokból álló üvegoszlopok laboratóriumi. vizsgálata. Jakab András, doktorandusz. BME, Építőanyagok és Magasépítés Tanszék
 Síklapokból álló üvegoszlopok laboratóriumi vizsgálata Előadó: Jakab András, doktorandusz BME, Építőanyagok és Magasépítés Tanszék Nehme Kinga, Nehme Salem Georges Szilikátipari Tudományos Egyesület Üvegipari
Síklapokból álló üvegoszlopok laboratóriumi vizsgálata Előadó: Jakab András, doktorandusz BME, Építőanyagok és Magasépítés Tanszék Nehme Kinga, Nehme Salem Georges Szilikátipari Tudományos Egyesület Üvegipari
PhD DISSZERTÁCIÓ TÉZISEI
 Budapesti Muszaki és Gazdaságtudományi Egyetem Fizikai Kémia Tanszék MTA-BME Lágy Anyagok Laboratóriuma PhD DISSZERTÁCIÓ TÉZISEI Mágneses tér hatása kompozit gélek és elasztomerek rugalmasságára Készítette:
Budapesti Muszaki és Gazdaságtudományi Egyetem Fizikai Kémia Tanszék MTA-BME Lágy Anyagok Laboratóriuma PhD DISSZERTÁCIÓ TÉZISEI Mágneses tér hatása kompozit gélek és elasztomerek rugalmasságára Készítette:
Készítsen elvi szabadkézi vázlatokat! Törekedjen a témával kapcsolatos lényeges jellemzők kiemelésére!
 1 6 ) M u t a s s a b e a s á r g a r é z c s ő v e z e t é k k é s z í t é s é t a z a l á b b i v á z l a t f e lh a s z n á l á s á v a l Készítsen elvi szabadkézi vázlatokat! Törekedjen a témával kapcsolatos
1 6 ) M u t a s s a b e a s á r g a r é z c s ő v e z e t é k k é s z í t é s é t a z a l á b b i v á z l a t f e lh a s z n á l á s á v a l Készítsen elvi szabadkézi vázlatokat! Törekedjen a témával kapcsolatos
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ)
 Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
ahol m-schmid vagy geometriai tényező. A terhelőerő növekedésével a csúszó síkban fellép az un. kritikus csúsztató feszültség τ
 Egykristály és polikristály képlékeny alakváltozása A Frenkel féle modell, hibátlan anyagot feltételezve, nagyon nagy folyáshatárt eredményez. A rácshibák, különösen a diszlokációk jelenléte miatt a tényleges
Egykristály és polikristály képlékeny alakváltozása A Frenkel féle modell, hibátlan anyagot feltételezve, nagyon nagy folyáshatárt eredményez. A rácshibák, különösen a diszlokációk jelenléte miatt a tényleges
PÉLDÁK ERŐTÖRVÉNYEKRE
 PÉLÁ ERŐTÖRVÉNYERE Szabad erők: erőtörvénnyel megadhatók, általában nem függenek a test mozgásállapotától (sebességtől, gyorsulástól) Példák: nehézségi erő, súrlódási erők, rugalmas erők, felhajtóerők,
PÉLÁ ERŐTÖRVÉNYERE Szabad erők: erőtörvénnyel megadhatók, általában nem függenek a test mozgásállapotától (sebességtől, gyorsulástól) Példák: nehézségi erő, súrlódási erők, rugalmas erők, felhajtóerők,
LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok
 LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok Budapest, 2004. 1 Tartalom 1. BEVEZETÉS... 4 1.1. A tervezési útmutató tárgya... 4 1.2. Az alkalmazott szabványok...
LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok Budapest, 2004. 1 Tartalom 1. BEVEZETÉS... 4 1.1. A tervezési útmutató tárgya... 4 1.2. Az alkalmazott szabványok...
Vasalttalaj hídfők. Tóth Gergő. Gradex Mérnöki és Szolgáltató Kft Budapest, Bécsi út 120. Telefon: +36-1/
 Vasalttalaj hídfők Tóth Gergő Gradex Mérnöki és Szolgáltató Kft. 1034 Budapest, Bécsi út 120. Telefon: +36-1/436-0990 www.gradex.hu Az előadás 1. Hagyományos hídfő kialakítások régen és most 2. Első hazai
Vasalttalaj hídfők Tóth Gergő Gradex Mérnöki és Szolgáltató Kft. 1034 Budapest, Bécsi út 120. Telefon: +36-1/436-0990 www.gradex.hu Az előadás 1. Hagyományos hídfő kialakítások régen és most 2. Első hazai
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására
 Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
Peltier-elemek vizsgálata
 Peltier-elemek vizsgálata Mérés helyszíne: Vegyész labor Mérés időpontja: 2012.02.20. 17:00-20:00 Mérés végrehatói: Budai Csaba Sánta Botond I. Seebeck együttható közvetlen kimérése Az adott P-N átmenetre
Peltier-elemek vizsgálata Mérés helyszíne: Vegyész labor Mérés időpontja: 2012.02.20. 17:00-20:00 Mérés végrehatói: Budai Csaba Sánta Botond I. Seebeck együttható közvetlen kimérése Az adott P-N átmenetre
KOMPOZITLEMEZ ORTOTRÓP
 KOMPOZITLEMEZ ORTOTRÓP ANYAGJELLEMZŐINEK MEGHATÁROZÁSA ÉS KÍSÉRLETI IGAZOLÁSA Nagy Anna anna.nagy@econengineering.com econ Engineering econ Engineering Kft. 2019 H-1116 Budapest, Kondorosi út 3. IV. emelet
KOMPOZITLEMEZ ORTOTRÓP ANYAGJELLEMZŐINEK MEGHATÁROZÁSA ÉS KÍSÉRLETI IGAZOLÁSA Nagy Anna anna.nagy@econengineering.com econ Engineering econ Engineering Kft. 2019 H-1116 Budapest, Kondorosi út 3. IV. emelet
PFEIFER - MoFi 16 Ferdetámaszok rögzítő rendszere. 2015.05.22 1.oldal
 PFEIFER - Ferdetámaszok rögzítő rendszere 2015.05.22 1.oldal Felhasználás Mire használjuk? A PFEIFER típusú ferde támaszok rögzítő rendszere ideiglenesen rögzíti a ferdetámaszokat a fejrésznél. Ferde támasztó
PFEIFER - Ferdetámaszok rögzítő rendszere 2015.05.22 1.oldal Felhasználás Mire használjuk? A PFEIFER típusú ferde támaszok rögzítő rendszere ideiglenesen rögzíti a ferdetámaszokat a fejrésznél. Ferde támasztó
ERŐVEL ZÁRÓ KÖTÉSEK (Vázlat)
 ERŐVEL ZÁRÓ KÖTÉSEK (Vázlat) Erővel záró nyomatékkötések Hatáselve: a kapcsolódó felületre merőleges rugalmas szorítás hatására a felület érintőjének irányába ható terheléssel ellentétes irányban ébredő
ERŐVEL ZÁRÓ KÖTÉSEK (Vázlat) Erővel záró nyomatékkötések Hatáselve: a kapcsolódó felületre merőleges rugalmas szorítás hatására a felület érintőjének irányába ható terheléssel ellentétes irányban ébredő
TERMÉKSZIMULÁCIÓ. Dr. Kovács Zsolt. Végeselem módszer. Elıadó: egyetemi tanár. Termékszimuláció tantárgy 6. elıadás március 22.
 TERMÉKZIMULÁCIÓ Végeselem módszer Termékszimuláció tantárgy 6. elıadás 211. március 22. Elıadó: Dr. Kovács Zsolt egyetemi tanár A végeselem módszer lényege A vizsgált, tetszıleges geometriai kialakítású
TERMÉKZIMULÁCIÓ Végeselem módszer Termékszimuláció tantárgy 6. elıadás 211. március 22. Elıadó: Dr. Kovács Zsolt egyetemi tanár A végeselem módszer lényege A vizsgált, tetszıleges geometriai kialakítású
ZAJCSILLAPÍTOTT SZÁMÍTÓGÉPHÁZ TERVEZÉSE
 ZAJCSILLAPÍTOTT SZÁMÍTÓGÉPHÁZ TERVEZÉSE Kovács Gábor 2006. április 01. TARTALOMJEGYZÉK TARTALOMJEGYZÉK... 2 1. FELADAT MEGFOGALMAZÁSA... 3 2. LÉGCSATORNA ZAJCSILLAPÍTÁSA... 3 2.1 Négyzet keresztmetszet...
ZAJCSILLAPÍTOTT SZÁMÍTÓGÉPHÁZ TERVEZÉSE Kovács Gábor 2006. április 01. TARTALOMJEGYZÉK TARTALOMJEGYZÉK... 2 1. FELADAT MEGFOGALMAZÁSA... 3 2. LÉGCSATORNA ZAJCSILLAPÍTÁSA... 3 2.1 Négyzet keresztmetszet...
A= a keresztmetszeti felület cm 2 ɣ = biztonsági tényező
 Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Matematika III előadás
 Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Fa- és Acélszerkezetek I. 10. Előadás Faszerkezetek I. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 10. Előadás Faszerkezetek I. Dr. Szalai József Főiskolai adjunktus Tartalom Fa, mint anyag általános tulajdonságai Előnyök-hátrányok Faipari termékek Faszerkezetek jellemző alkalmazási
Fa- és Acélszerkezetek I. 10. Előadás Faszerkezetek I. Dr. Szalai József Főiskolai adjunktus Tartalom Fa, mint anyag általános tulajdonságai Előnyök-hátrányok Faipari termékek Faszerkezetek jellemző alkalmazási
Mechanika I-II. Példatár
 Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
1. Feladat. a) Mekkora radiális, tangenciális és axiális feszültségek ébrednek a csőfalban, ha a csővég zárt?
 1. Feladat Egy a = mm első és = 150 mm külső sugarú cső terhelése p = 60 MPa első ill. p k = 30 MPa külső nyomás. a) Mekkora radiális, tangenciális és axiális feszültségek érednek a csőfalan, ha a csővég
1. Feladat Egy a = mm első és = 150 mm külső sugarú cső terhelése p = 60 MPa első ill. p k = 30 MPa külső nyomás. a) Mekkora radiális, tangenciális és axiális feszültségek érednek a csőfalan, ha a csővég
Jellemző szelvények alagút
 Alagútépítés Jellemző szelvények alagút 50 50 Jellemző szelvény - alagút 51 AalagútDél Nyugati járat Keleti járat 51 Alagúttervezés - geotechnika 52 Technológia - Új osztrák építési módszer (NÖT) 1356
Alagútépítés Jellemző szelvények alagút 50 50 Jellemző szelvény - alagút 51 AalagútDél Nyugati járat Keleti járat 51 Alagúttervezés - geotechnika 52 Technológia - Új osztrák építési módszer (NÖT) 1356
Alagútépítés 3. Előadásanyag 3.2 rész Ideiglenes biztosítás
 Alagútépítés 3. Előadásanyag 3.2 rész Ideiglenes biztosítás Tóth Ákos Szepesházi Róbert 1 Megtámasztási rendszerek 1. A biztosítás és a kőzetdeformáció összefüggenek. A biztosításra ható teher függ a kőzet
Alagútépítés 3. Előadásanyag 3.2 rész Ideiglenes biztosítás Tóth Ákos Szepesházi Róbert 1 Megtámasztási rendszerek 1. A biztosítás és a kőzetdeformáció összefüggenek. A biztosításra ható teher függ a kőzet
A KŐZETMECHANIKAI LABORATÓRIUM AKKOR ÉS MA"
 A Miskolci Egyetem Közleményei, A sorozat, Bányászat, 76. kötet (2009), p. 129-156. A KŐZETMECHANIKAI LABORATÓRIUM AKKOR ÉS MA" Dr. Debreczeni Ákos egyetemi docens Miskolci Egyetem, Bányászati és Geotechnikai
A Miskolci Egyetem Közleményei, A sorozat, Bányászat, 76. kötet (2009), p. 129-156. A KŐZETMECHANIKAI LABORATÓRIUM AKKOR ÉS MA" Dr. Debreczeni Ákos egyetemi docens Miskolci Egyetem, Bányászati és Geotechnikai
Folyadékszcintillációs spektroszkópia jegyz könyv
 Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Alapcsavar FBN II Milliószor bizonyított, rugalmas az ár és a teljesítmény tekintetében.
 1 Milliószor bizonyított, rugalmas az ár és a teljesítmény tekintetében. Áttekintés FBN II cinkkel galvanizált acél FBN II A4 korrózióálló acél, III-as korrózióállósági osztály, pl. A4 FBN II fvz* tüzihorganyzott
1 Milliószor bizonyított, rugalmas az ár és a teljesítmény tekintetében. Áttekintés FBN II cinkkel galvanizált acél FBN II A4 korrózióálló acél, III-as korrózióállósági osztály, pl. A4 FBN II fvz* tüzihorganyzott
A MÁV-Thermit Kft, valamint a BME Út és Vasútépítési Tanszék köszönti az előadás hallgatóit
 MÁV THERMIT Kft Városi vasutak szakmai nap Balatonfenyves, 2010. 03. 18-19. A MÁV-Thermit Kft, valamint a BME Út és Vasútépítési Tanszék köszönti az előadás hallgatóit Hézagnélküli vágányok stabilitása
MÁV THERMIT Kft Városi vasutak szakmai nap Balatonfenyves, 2010. 03. 18-19. A MÁV-Thermit Kft, valamint a BME Út és Vasútépítési Tanszék köszönti az előadás hallgatóit Hézagnélküli vágányok stabilitása
Acélszerkezetek. 3. előadás 2012.02.24.
 Acélszerkezetek 3. előadás 2012.02.24. Kapcsolatok méretezése Kapcsolatok típusai Mechanikus kapcsolatok: Szegecsek Csavarok Csapok Hegesztett kapcsolatok Tompavarrat Sarokvarrat Coalbrookdale, 1781 Eiffel
Acélszerkezetek 3. előadás 2012.02.24. Kapcsolatok méretezése Kapcsolatok típusai Mechanikus kapcsolatok: Szegecsek Csavarok Csapok Hegesztett kapcsolatok Tompavarrat Sarokvarrat Coalbrookdale, 1781 Eiffel
Csavarkötés mérése ), (5) μ m a menetes kapcsolat súrlódási tényezője, β a menet élszöge. 1. Elméleti alapok
 GEGE-AGG labormérések Csavarkötés mérése. Elméleti alapok Csavarkötéseknél az összekapcsolt alkatrészek terhelés alatti elmozdulásának megakadályozása céljából előfeszítést kell alkalmazni, amelynek nagyságát
GEGE-AGG labormérések Csavarkötés mérése. Elméleti alapok Csavarkötéseknél az összekapcsolt alkatrészek terhelés alatti elmozdulásának megakadályozása céljából előfeszítést kell alkalmazni, amelynek nagyságát
Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások
 Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
E-mail: info@silliker.hu web: www.silliker.hu Telefon: +36-30-479-1802
 Pom T-206/3 szállítócsiga Műszaki adatok : T-206/3 4-9 t/h Alapgép hossza (m) 4 Maximális hossz (m) 6 1,7* 4,3** 60⁰ Belső átmérő (mm) 100 1,5 1420 Gép tömege (kb) 80 Kiegészítő tartozékok: fogadógarat
Pom T-206/3 szállítócsiga Műszaki adatok : T-206/3 4-9 t/h Alapgép hossza (m) 4 Maximális hossz (m) 6 1,7* 4,3** 60⁰ Belső átmérő (mm) 100 1,5 1420 Gép tömege (kb) 80 Kiegészítő tartozékok: fogadógarat
Poncelet egy tételéről
 1 Poncelet egy tételéről Már régebben találkoztunk az [ 1 ] műben egy problémával, mostanában pedig a [ 2 ] műben a megoldásával. A probléma lényege: határozzuk meg a egyenletben szereplő α, β együtthatókat,
1 Poncelet egy tételéről Már régebben találkoztunk az [ 1 ] műben egy problémával, mostanában pedig a [ 2 ] műben a megoldásával. A probléma lényege: határozzuk meg a egyenletben szereplő α, β együtthatókat,
Földstatikai feladatok megoldási módszerei
 Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI FOLYAMATÁNAK ELEMZÉSE
 Budapest M szaki és Gazdaságtudományi Egyetem Polimertecnika Tanszék EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI OLYAMATÁNAK ELEMZÉSE Tézisek Rácz Zsolt Témavezet
Budapest M szaki és Gazdaságtudományi Egyetem Polimertecnika Tanszék EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI OLYAMATÁNAK ELEMZÉSE Tézisek Rácz Zsolt Témavezet
Az utóbbi állításnál a képlettel bizonyítható az állítás helyessége, mivel erő szorozva erőkarral
 Bevezetés, alapfogalmak A csörlődobon a kötél rétegekből épül fel, ahogy a képen látható, ebből következik, hogy felcsévélés közben a kötéldobon található kötélrétegnek a kerülete folyamatosan növekszik,
Bevezetés, alapfogalmak A csörlődobon a kötél rétegekből épül fel, ahogy a képen látható, ebből következik, hogy felcsévélés közben a kötéldobon található kötélrétegnek a kerülete folyamatosan növekszik,
MŰANYAGOK ALKALMAZÁSA
 MŰANYAGOK ALKALMAZÁSA Geoműanyagok A környezetszennyeződés megakadályozása érdekében a szemétlerakókat környezetüktől hosszú távra el kell szigetelni. Ebben nagy szerepük van a műanyag geomembránoknak.
MŰANYAGOK ALKALMAZÁSA Geoműanyagok A környezetszennyeződés megakadályozása érdekében a szemétlerakókat környezetüktől hosszú távra el kell szigetelni. Ebben nagy szerepük van a műanyag geomembránoknak.
A talajok összenyomódásának vizsgálata
 A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
Korrodált acélszerkezetek vizsgálata
 Korrodált acélszerkezetek vizsgálata 1. Szerkezeti példák és laboratóriumi alapkutatás Oszvald Katalin Témavezető : Dr. Dunai László Budapest, 2009.12.08. 1 Általános célkitűzések Korrózió miatt károsodott
Korrodált acélszerkezetek vizsgálata 1. Szerkezeti példák és laboratóriumi alapkutatás Oszvald Katalin Témavezető : Dr. Dunai László Budapest, 2009.12.08. 1 Általános célkitűzések Korrózió miatt károsodott
Tevékenység: Gyűjtse ki és tanulja meg a kötőcsavarok szilárdsági tulajdonságainak jelölési módját!
 Csavarkötés egy külső ( orsó ) és egy belső ( anya ) csavarmenet kapcsolódását jelenti. A következő képek a motor forgattyúsházában a főcsapágycsavarokat és a hajtókarcsavarokat mutatják. 1. Kötőcsavarok
Csavarkötés egy külső ( orsó ) és egy belső ( anya ) csavarmenet kapcsolódását jelenti. A következő képek a motor forgattyúsházában a főcsapágycsavarokat és a hajtókarcsavarokat mutatják. 1. Kötőcsavarok
Fa- és Acélszerkezetek I. 7. Előadás Kapcsolatok I. Csavarozott kapcsolatok. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 7. Előadás Kapcsolatok I. Csavarozott kapcsolatok Dr. Szalai József Főiskolai adjunktus Tartalom Acélszerkezetek kapcsolatai Csavarozott kapcsolatok kialakítása Csavarozott kapcsolatok
Fa- és Acélszerkezetek I. 7. Előadás Kapcsolatok I. Csavarozott kapcsolatok Dr. Szalai József Főiskolai adjunktus Tartalom Acélszerkezetek kapcsolatai Csavarozott kapcsolatok kialakítása Csavarozott kapcsolatok
Gyakorlati példák Dr. Gönczi Dávid
 Szilárdságtani számítások Gyakorlati példák Dr. Gönczi Dávid I. Bevezető ismeretek I.1 Definíciók I.2 Tenzoralgebrai alapismeretek I.3 Bevezetés az indexes jelölésmódba I.4 A lineáris rugalmasságtan általános
Szilárdságtani számítások Gyakorlati példák Dr. Gönczi Dávid I. Bevezető ismeretek I.1 Definíciók I.2 Tenzoralgebrai alapismeretek I.3 Bevezetés az indexes jelölésmódba I.4 A lineáris rugalmasságtan általános
5. fejezet. Differenciálegyenletek
 5. fejezet Differenciálegyenletek 5.. Differenciálegyenletek 5... Szeparábilis differenciálegyenletek 5.. Oldjuk meg az alábbi differenciálegyenleteket, és ábrázoljunk néhány megoldást. a) y = x. b) y
5. fejezet Differenciálegyenletek 5.. Differenciálegyenletek 5... Szeparábilis differenciálegyenletek 5.. Oldjuk meg az alábbi differenciálegyenleteket, és ábrázoljunk néhány megoldást. a) y = x. b) y
λx f 1 (x) e λx f 2 (x) λe λx f 2 (x) + e λx f 2(x) e λx f 2 (x) Hasonlóan általában is elérhető sorműveletekkel, hogy csak f (j)
 Matematika A3 gyakorlat Energetika és Mechatronika BSc szakok, 016/17 ősz 10 feladatsor: Magasabbrendű lineáris differenciálegyenletek (megoldás) 1 Határozzuk meg az e λx, xe λx, x e λx,, x k 1 e λx függvények
Matematika A3 gyakorlat Energetika és Mechatronika BSc szakok, 016/17 ősz 10 feladatsor: Magasabbrendű lineáris differenciálegyenletek (megoldás) 1 Határozzuk meg az e λx, xe λx, x e λx,, x k 1 e λx függvények
Attól, hogy nem inog horizontális irányban a szélességi- és hosszúsági tengelye körül sem.
 Konkrét tanácsok a Salgó-dexion polcrendszer összeszereléséhez Vásárlásunk során a Salgó-dexion polcokat, polcrendszereket sokféle módon állíthatjuk össze az igénybe vételnek, felhasználásnak, valamint
Konkrét tanácsok a Salgó-dexion polcrendszer összeszereléséhez Vásárlásunk során a Salgó-dexion polcokat, polcrendszereket sokféle módon állíthatjuk össze az igénybe vételnek, felhasználásnak, valamint
NSZ/NT beton és hídépítési alkalmazása
 NSZ/NT beton és hídépítési alkalmazása Farkas Gy.-Huszár Zs.-Kovács T.-Szalai K. R forgalmi terhelésű utak - megnövekedett forgalmi terhelés - fokozott tartóssági igény - fenntartási idő és költségek csökkentése
NSZ/NT beton és hídépítési alkalmazása Farkas Gy.-Huszár Zs.-Kovács T.-Szalai K. R forgalmi terhelésű utak - megnövekedett forgalmi terhelés - fokozott tartóssági igény - fenntartási idő és költségek csökkentése
SIKLÓCSAPÁGY KISFELADAT
 Dr. Lovas Lászl SIKLÓCSAPÁGY KISFELADAT Segédlet a Jármű- és hajtáselemek II. tantárgyhoz Kézirat 2012 SIKLÓCSAPÁGY KISFELADAT 1. Adatválaszték pk [MPa] d [mm] b/d [-] n [1/min] ház anyaga 1 4 50 1 1440
Dr. Lovas Lászl SIKLÓCSAPÁGY KISFELADAT Segédlet a Jármű- és hajtáselemek II. tantárgyhoz Kézirat 2012 SIKLÓCSAPÁGY KISFELADAT 1. Adatválaszték pk [MPa] d [mm] b/d [-] n [1/min] ház anyaga 1 4 50 1 1440
GÖRGŐS LÁNCHAJTÁS tervezése
 MISKOLCI EGYETEM GÉPELEMEK TANSZÉKE OKTATÁSI SEGÉDLET a GÉPELEMEK II. c. tantárgyhoz GÖRGŐS LÁNCHAJTÁS tervezése Összeállította: Dr. Szente József egyetemi docens Miskolc, 008. A lánchajtás tervezése során
MISKOLCI EGYETEM GÉPELEMEK TANSZÉKE OKTATÁSI SEGÉDLET a GÉPELEMEK II. c. tantárgyhoz GÖRGŐS LÁNCHAJTÁS tervezése Összeállította: Dr. Szente József egyetemi docens Miskolc, 008. A lánchajtás tervezése során
Lövés csúzlival. Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk ki!
 1 Lövés csúzlival Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. A feladat Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk
1 Lövés csúzlival Az [ 1 ] munkában találtuk az alábbi feladatot 1. ábra. A feladat Egy csúzli k merevségű gumival készült. Adjuk meg az ebből kilőtt m tömegű lövedék sebességét, ha a csúzlit L - re húztuk
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL
 SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
Lineáris algebra numerikus módszerei
 Hermite interpoláció Tegyük fel, hogy az x 0, x 1,..., x k [a, b] különböző alappontok (k n), továbbá m 0, m 1,..., m k N multiplicitások úgy, hogy Legyenek adottak k m i = n + 1. i=0 f (j) (x i ) = y
Hermite interpoláció Tegyük fel, hogy az x 0, x 1,..., x k [a, b] különböző alappontok (k n), továbbá m 0, m 1,..., m k N multiplicitások úgy, hogy Legyenek adottak k m i = n + 1. i=0 f (j) (x i ) = y
2.9.1. TABLETTÁK ÉS KAPSZULÁK SZÉTESÉSE
 2.9.1 Tabletták és kapszulák szétesése Ph.Hg.VIII. Ph.Eur.6.3-1 01/2009:20901 2.9.1. TABLETTÁK ÉS KAPSZULÁK SZÉTESÉSE A szétesésvizsgálattal azt határozzuk meg, hogy az alábbiakban leírt kísérleti körülmények
2.9.1 Tabletták és kapszulák szétesése Ph.Hg.VIII. Ph.Eur.6.3-1 01/2009:20901 2.9.1. TABLETTÁK ÉS KAPSZULÁK SZÉTESÉSE A szétesésvizsgálattal azt határozzuk meg, hogy az alábbiakban leírt kísérleti körülmények
T s 2 képezve a. cos q s 0; 2. Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról
 Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról Úgy találjuk, hogy a kötelek statikájának népszerűsítése egy soha véget nem érő feladat. Annyi szép dolog tárháza
Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról Úgy találjuk, hogy a kötelek statikájának népszerűsítése egy soha véget nem érő feladat. Annyi szép dolog tárháza
Diplomamunkám felépítése
 Üregek távolhatása gránitos kőzetkörnyezetben Tóth Szilvia Konzulensek: Dr. Török Ákos, BME Építőanyagok és Mérnökgeológia Tanszék Poromb Péter, Mott MacDonald Magyarország Kft. Diplomamunkám felépítése
Üregek távolhatása gránitos kőzetkörnyezetben Tóth Szilvia Konzulensek: Dr. Török Ákos, BME Építőanyagok és Mérnökgeológia Tanszék Poromb Péter, Mott MacDonald Magyarország Kft. Diplomamunkám felépítése
 Körgyűrű keresztmetszetű, pörgetett vasbeton rudak nyírási ellenállása 1. rész Völgyi István Témavezető: Dr Farkas György Kutatás felépítése 1. Anyagvizsgálatok 2. Nyírási ellenállás 3. Modellalkotás -
Körgyűrű keresztmetszetű, pörgetett vasbeton rudak nyírási ellenállása 1. rész Völgyi István Témavezető: Dr Farkas György Kutatás felépítése 1. Anyagvizsgálatok 2. Nyírási ellenállás 3. Modellalkotás -
Mikrocölöp alapozás ellenőrzése
 36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
Egy érdekes mechanikai feladat
 1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Az M0 Megyeri híd próbaterhelése Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke
 Az M0 Megyeri híd próbaterhelése Dr. Dunai László egyetemi tanár BME, Próbaterhelési terv - kidolgozás Balparti ártéri híd - 2 híd, BME Céh Zrt. Jobbparti ártéri híd - 2 híd, BME Céh Zrt. Szentendrei-sziget
Az M0 Megyeri híd próbaterhelése Dr. Dunai László egyetemi tanár BME, Próbaterhelési terv - kidolgozás Balparti ártéri híd - 2 híd, BME Céh Zrt. Jobbparti ártéri híd - 2 híd, BME Céh Zrt. Szentendrei-sziget
Anyagvizsgálatok. Mechanikai vizsgálatok
 Anyagvizsgálatok Mechanikai vizsgálatok Szakítóvizsgálat EN 10002-1:2002 Célja: az anyagok egytengelyű húzó igénybevétellel szembeni ellenállásának meghatározása egy szabványosan kialakított próbatestet
Anyagvizsgálatok Mechanikai vizsgálatok Szakítóvizsgálat EN 10002-1:2002 Célja: az anyagok egytengelyű húzó igénybevétellel szembeni ellenállásának meghatározása egy szabványosan kialakított próbatestet
Tipikus fa kapcsolatok
 Tipikus fa kapcsolatok Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék 1 Gerenda fal kapcsolatok Gerenda feltámaszkodás 1 Vízszintes és (lefelé vagy fölfelé irányuló) függőleges terhek
Tipikus fa kapcsolatok Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék 1 Gerenda fal kapcsolatok Gerenda feltámaszkodás 1 Vízszintes és (lefelé vagy fölfelé irányuló) függőleges terhek
Mérés: Millikan olajcsepp-kísérlete
 Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Lemez- és gerendaalapok méretezése
 Lemez- és gerendaalapok méretezése Az alapmerevség hatása az alap hajlékony merev a talpfeszültség egyenletes széleken nagyobb a süllyedés teknıszerő egyenletes Terhelés hatása hajlékony alapok esetén
Lemez- és gerendaalapok méretezése Az alapmerevség hatása az alap hajlékony merev a talpfeszültség egyenletes széleken nagyobb a süllyedés teknıszerő egyenletes Terhelés hatása hajlékony alapok esetén
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 6.2. fejezet 483 FEJEZET BEVEZETŐ 6.2. fejezet: Síkalapozás (vb. lemezalapozás) Az irodaház szerkezete, geometriája, a helyszín és a geotechnikai adottságok is megegyeznek az előző (6.1-es) fejezetben
6.2. fejezet 483 FEJEZET BEVEZETŐ 6.2. fejezet: Síkalapozás (vb. lemezalapozás) Az irodaház szerkezete, geometriája, a helyszín és a geotechnikai adottságok is megegyeznek az előző (6.1-es) fejezetben
a textil-szövet hosszirányú szálainak és a teljes szálmennyiségnek a térfogati aránya,
 Zárójelentés A kutatás kezdetén felmértük a polimer kompozitok fajtáit és az alkalmazott gyártási eljárásokat. Mindezt annak érdekében tettük, hogy a kapott eredmények alkalmazhatósági határait kijelölhessük.
Zárójelentés A kutatás kezdetén felmértük a polimer kompozitok fajtáit és az alkalmazott gyártási eljárásokat. Mindezt annak érdekében tettük, hogy a kapott eredmények alkalmazhatósági határait kijelölhessük.
GONDOLATOK A BIZTOSÍTÓSZERKEZETEK CÉLSZERŰ BEÉPÍTÉSI IDEJÉRŐL ÉS A PÓTBIZTOSÍTÁSOK SZEREPÉRŐL DEBRECZENI ÁKOS 1
 Műszaki Földtudományi Közlemények, 86. kötet, 1. szám (2017), pp. 23 29. GONDOLATOK A BIZTOSÍTÓSZERKEZETEK CÉLSZERŰ BEÉPÍTÉSI IDEJÉRŐL ÉS A PÓTBIZTOSÍTÁSOK SZEREPÉRŐL DEBRECZENI ÁKOS 1 Absztrakt: A föld
Műszaki Földtudományi Közlemények, 86. kötet, 1. szám (2017), pp. 23 29. GONDOLATOK A BIZTOSÍTÓSZERKEZETEK CÉLSZERŰ BEÉPÍTÉSI IDEJÉRŐL ÉS A PÓTBIZTOSÍTÁSOK SZEREPÉRŐL DEBRECZENI ÁKOS 1 Absztrakt: A föld
A forgójeladók mechanikai kialakítása
 A forgójeladók mechanikai kialakítása A különböző gyártók néhány szabványos kiviteltől eltekintve nagy forma- és méretválasztékban kínálják termékeiket. Az elektromos illesztéshez hasonlóan a mechanikai
A forgójeladók mechanikai kialakítása A különböző gyártók néhány szabványos kiviteltől eltekintve nagy forma- és méretválasztékban kínálják termékeiket. Az elektromos illesztéshez hasonlóan a mechanikai
DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT
 DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT 2013 Feladat: Adott az ábrán látható kéttámaszú tartó, amely melegen hengerelt I idomacélokból és melegen hengerelt
DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT 2013 Feladat: Adott az ábrán látható kéttámaszú tartó, amely melegen hengerelt I idomacélokból és melegen hengerelt
MFI mérés BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA
 B1 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK MFI mérés HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA A JEGYZET ÉRVÉNYESSÉGÉT A TANSZÉKI WEB OLDALON
B1 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK MFI mérés HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA A JEGYZET ÉRVÉNYESSÉGÉT A TANSZÉKI WEB OLDALON
