Hatékony konvolúciós neurális hálózat tervezése osztályozási problémákra
|
|
|
- Csenge Fülöp
- 5 évvel ezelőtt
- Látták:
Átírás
1 Hatékony konvolúciós neurális hálózat tervezése osztályozási problémákra Formanek András - mérnök informatikus BSc 4. évf Konzulens: Hadházi Dániel Méréstechnika és Információs Rendszerek Tanszék Budapest, október 26.
2 Tartalom Bevezetés... 3 Szakirodalom áttekintése Kapcsolódó kutatások Paraméter kvantálás és binarizálás Paraméter nyesés és megosztás Alacsony rangú faktorizáció és ritkítás Rétegengénti relevancia visszaterjesztés Tudás desztillálás Felhasznált fogalmak Módszer bemutatása Felhasználási példa (Soft Decision Trees)... 9 Klasszikus paraméterredukció desztillálással Redundáns szűrők eliminálása Geometriai torzítások Uniformizálás Uniformizálás neurális hálóval Tapasztalati eredmények Összefoglalás Háló tanítása L0 regularizációval Motiváció Regularizáció Súlyok regularizálása csoportosan Megvalósítás Tapasztalatok Összefoglalás Összefoglalás, továbbfejlesztési lehetőségek Irodalomjegyzék Függelék... 33
3 Bevezetés Az elmúlt néhány évben a konvolúciós neurális hálózatok megreformálták a képfeldolgozás területét. Sok probléma esetén utolérték és meghaladták a klasszikus, szakértői képfeldolgozó módszerek pontosságát és hatékonyságát. Egyelőre nem mutat semmilyen jel arra, hogy a neurális paradigma ilyen jellegű, egyre szélesebb körű alkalmazásának térnyerése ne folytatódna. Azonban ezek az új megoldások gyakorlatilag feketedoboz jellegűek még azok számára is, akik értik, hogy általánosan hogyan működnek a neurális paradigma eszközei. Bár a tanulás folyamata világos, a megtanult tudás reprezentációja nehezen interpretálható. Így azon kívül, hogy meg tudjuk mérni, hogy az általunk gyűjtött, korlátos mintakészlet mekkora részére működik helyesen az adott megoldás, arra már nehezebb választ adni, hogy miért és milyen esetekben fog helytelen kimenetet előállítani. Ilyen jellegű bizonytalanságok nem engedhetőek meg biztonságkritikus rendszerek (például az önvezető autók) esetében, ahol emberi élet múlhat a rendszer hibás döntésein. Továbbá az is világossá vált, hogy nem csak a neurális paradigmán alapuló megoldások eseti hibáitól kell tartanunk, hanem lehetőség van a bemeneti képek olyan módon való manipulálására is, aminek hatására a megoldás helytelenül működik. További probléma, hogy a state-of-the-art eredmények olyan neurális hálókon alapulnak, melyek sok, akár több száz réteggel és több millió konvolúciós szűrővel rendelkeznek. Ez a magas komplexitás a már említett interpretálhatóság problémája mellett felvet még egyéb hatékonysági problémákat is. Tipikusan százmilliós nagyságrendbeli paraméter tanulása és tárolása szükséges. Ennek következtében mind a tanítási, mind egy minta esetén a háló válaszának előállításhoz szükséges erőforrásigény is nagy. A nagyméretű és emiatt lomha hálók pedig ugyancsak hátrányt jelenthetnek bizonyos ipari felhasználásokban. Példaként itt is maradjunk az önvezető autóknál: ha a háló nem képes elég gyorsan döntést hozni, hogy kell-e fékezni adott szituációban, akkor alkalmassága megkérdőjeleződik. A hálók paraméterszámbeli és számítási erőforrásigény szerinti hatékonysága tehát ma kulcskérdés, és várhatóan az is marad az éles, gyakorlati alkalmazások esetén a jövőben is. Munkám során 1 olyan módszereket vizsgáltam meg és tettem javaslatot módosításokra, hatásosságuk növelésére, melyekkel a fenti problémák enyhíthetők. Tételesen megvizsgáltam a tudás desztillálás alapú háló kompressziót, a Spatial Transformer réteg ilyen szempont szerinti alkalmazhatóságát, valamint javaslatot tettem a ma népszerű direkt regularizációs módszerek ilyen célból történő adaptálására. Minden taglalt módosítás hatását kvantitatívan és kvalitatívan is elemeztem, melyek eredményeképpen megállapítottam, hogy jelentős hatékonyságnövekedés érhető el a pontosság minimális szintű redukciója mellett. 1 A dolgozatban taglalt kutatás az Európai Unió támogatásával, az Európai Regionális Fejlesztési Alap társfinanszírozásával valósul meg (EFOP ). df/ pdf
4 A dolgozat felépítése az alábbi: a 2. fejezetben szakirodalomban publikált megközelítéseket tekintem át, a 3. fejezetben a tudásdesztilláció alapú paraméterredukciót mutatom be, a 4. fejezet a redundáns szűrések eliminálását taglalja, az 5. fejezetben összefoglalom az elért eredményeket és a hozzájuk kapcsolódó konklúziókat is levonom. A dolgozatnak részét képezi egy kétoldalas függelék is.
5 Szakirodalom áttekintése 2.1 Kapcsolódó kutatások Ebben a fejezetben bemutatom a már ismert techológiákat, melyek célja konvolúciós neurális hálók (CNN), paraméterszámának csökkentése, vagy működésük átláthatóbbá tétele. Első esetben az erőforrás igény, második esetben az interpretálhatóság felől megközelítve értelmeztem, és próbáltam javítani a hatékonyságot Paraméter kvantálás és binarizálás A paraméterek durvább granularitású ábrázolásával jelentősen redukálható a hálók tárolásához szükséges memória mérete. Ennek szélsőséges esete a binarizálás, amikor a háló összes súlya csak a 0 vagy az 1 értéket veheti fel, de ennél finomabb felosztás is elképzelhető. Például 8 bit, ahogy [7]-ben olvashatjuk. Itt az elsődleges cél az volt, hogy a modell CPU-n is futtatható legyen, és sikerült is 3-4-szeres gyorsulást elérniük, a lebegőpontos helyetti fixpontos ábrázolással, miközben a modell pontossága alig romlott. 16-bites ábrázolást is megvizsgált a szakirodalom: [8]. Összehasonlításképpen, az általában használt lebegőpontos float típus a C és C++ nyelvekben többnyire 32 bit, míg Pythonban 64 bit Paraméter nyesés és megosztás A megközelítés lényege, hogy a hálónak valamilyen szempontból haszontalan részeit eldobjuk (nyesés) vagy más részeiből származtatjuk (megosztás), ezzel csökkentve a tanulandó paraméterek számát. A javasolt metódusok között találunk olyat, ami az összes súlyra megvizsgálja, hogy annak eldobása mennyivel növelné a háló hibáját, majd az így sorba állított súlyok közül adott számút kinulláz [9]. Ez a módszer tehát a nyeséshez is használja az adathalmazt, hogy hibát tudjon számolni. Olyan módszer is létezik, ami súlyok helyett neuronokat céloz. A [10] javasolt módszere, hogy ha két neuron által tanult súlyok közel egyenlőek, akkor az egyik neuront dobjuk el, a másikat pedig, a következő rétegben vegyük figyelembe, az eddigi két neuron súlyának összegével. Látható, hogy ennek a módszernek a kimenete nem függ az adatoktól. Mindkét módszerrel jelentősen csökkenthető a paraméterszám Alacsony rangú faktorizáció és ritkítás Az eddig említett módszerek többnyire csak a fully-connected rétegekre fókuszáltak. Ez érthető is, hiszen CNN-ek esetében is az utolsó pár réteg általában ilyen, és a tanulandó paraméterek nagy része ezekben lokalizálódik. Azonban a számítási idő nagy része még így is a relatíve lassan elvégezhető sok dimenziós konvolúciók számításából származik. Például, ha minden 2D konvolúciót helyettesíteni tudunk két 1D konvolúcióval, szignifikáns gyorsulás érhető el, úgy, hogy közben a pontosságból nem veszítünk sokat. A [11] ezt az ötletet tárgyalja. Ha az intuitívabb (bemeneti csatorna szám) x (kimeneti csatorna szám) db 2D konvolúció elvégzése helyett 1db 4D konvolúcióként gondolunk egy konvolúcuiós rétegre, akkor ezt a 4D tenzort jó közelítéssel alacsonyabb dimenziójú mátrixok szorzatára
6 bonthatjuk és a konvolúciókat külön-külön végezhetjük el. Ezzel a módszerrel a [11] alapján 2-3-szoros gyorsulást érhető el a pontosság elhanyagolható mértékű csökkenése mellett Rétegengénti relevancia visszaterjesztés A Layer-wise Relevance Propagation (LRP) [14] egy a neurális hálók tanítása során használt hiba visszaterjesztési (backward propagation) algoritmushoz hasonló technika, melyet kifejezetten magyarázási szándékkal terveztek. A módszer a bemeneti kép pixeleihez súlyokat rendel, melyek a döntéshozás szempontjából az adott pixel relevanciáját minősítik. Működését tekintve az l. réteg relevanciáit (R i (l) ) a következő réteg relevanciáinak (R j (l+1) ) függvényében írjuk fel, majd a kimeneti rétegtől elindulva visszaterjesztjük a relevanciákat, amíg el nem érjük a bemenetet. A visszaterjesztési szabályok származtatása az egyes neuronok definiált relevanciájának (pl. R i (l) ) alacsony fokszámú Taylor-polinomos közelítésén alapul. Osztályozási problémák esetén R (L) = f(x), ahol R (L) az utolsó réteg relevanciája f(x) pedig a háló kimenete. 1. ábra Az ábra a [14] cikkből származik. Mindkét képhármas balról jobbra: eredeti kép,a pixelenkénti relevancia és a bemeneti kép kiemelt éleinek a szuperpozíciója, végül az eredeti kép és a binarizált relevanciák szuperpozíciója. Az LRP eredményét az 1. ábra szemlélteti. A módszer előnye, hogy direkt alkalmazható bármilyen neurális hálóra, nem kell azon változtatni, tovább vagy újratanítani. Hátránya, hogy a relevancia visszaterjesztési szabályok származtatása során jelentős relaxációkat alkalmaz. A magyarázatgeneráló módszerek objektív összehasonlítása nehéz feladat, mivel nem léteznek jól definiált kvantitatív minősítők. Kvalitatív taksálás alapján viszont ez jelenleg a state-of-the-art eljárás. 2.2 Tudás desztillálás Felhasznált fogalmak Indokolt a következő módszer alaposabb bemutatása, mivel munkám során ezt is használtam. Ehhez szeretnék néhány olyan fogalmat tisztázni, vagy elnevezni, amit körülményes lenne a módszer bemutatás közben. Ezeket a szavakat a dolgozatom során így fogom használni. target: A felügyelt tanítás során a tanítóhalmaz összeállítása után (pl. fényképek gyűjtése), minden adatpontról (képről) megállapítjuk, hogy melyik osztályba tartozik. Hibaeloszlásokból származtatott büntetőfüggvények esetén (mint amilyen pl. a kereszt entrópia is) ez jellemzően one-hot kódolt n elemű vektor hozzárendelését jelenti elvárt kimenetként, ahol n az osztályok száma. Például a j. oszály esetén e j.
7 Ezt az adatponthoz hozzárendelt vektort angol nevén magyarul is legtöbbször target -nek, vagyis célnak nevezzük. A felügyelt tanítás során a célunk, hogy a modell ezeket a targeteket minél kisebb hibával megközelítse. Az empirikus kockázat-minimalizálás során ezt a tanító pontokra direkt optimalizációval érjük el, viszont fontos kritérium, hogy a tanítás során nem látott képekre is helyes eredményt adjon (általánosító képesség). háló struktúra: A neurális hálók struktúrája alatt azon paramétereket értem, melyek nem változnak a tanítás során. softmax-with-temperature: A softmax gyakran használt aktivációs réteg. Leggyakrabban osztályozási problémák utolsó rétegének aktivációjaként használt, mivel a kimeneti vektor a különböző osztályokba tartozást leíró valószínűségi változó eloszlásaként értelmezhető (ld. logisztikus regresszió). Aktivációs függvényről lévén szó a bemeneti és kimeneti vektorok elemszáma megegyezik. Az aktivációhoz használt Boltzman-eloszlás definíciója: q i = e z j j T (1) Ahol z a bemeneti, q a kimeneti vektor, T pedig a temperature (hőmérséklet tényező). Leggyakoribb esetben a T = 1 helyettesítést használjuk. Kisebb T érték választása (a bemenet változatlanul hagyása mellett) nagyobb szórású kimeneti vektort eredményez, ugyanígy nagyobb érték választása kisebb szórásút. A kimeneti vektor elemei között azonban a kisebb-nagyobb relációk nem változnak, így maximum kiválasztás esetén a háló válasza sem. A softmax működését különböző hőmérsékletekkel az 2. ábrán szemléltetem. Látható, hogy a kimenetek között az elemek kisebb-nagyobb relációjában és átlagukban nincsen különbség, csak a szórásuk változik. e z i T 2. ábra A softmax aktiváció kimenete a választott hőmérséklet (T) függvényében. A bal felső ábrán egy minta z vektor látható. A többi ábrán a softmax kimenete különböző hőmérsékleteken.
8 2.2.2 Módszer bemutatása A tudás desztillálás, vagy angol nevén Knowledge Distillation (KD) eredeti ötlete a szakértő együttesek alkalmazásán alapszik. Hiszen ha egy osztályozási problémához megfelelően adaptálható neurális hálót többször, többféle (random) inicializálás után újratanítunk, akkor az így kapott modellek predikcióit átlagolva az adekvát osztályozás valószínűsége nagyobb, mint csak egy szakértő válaszának használata esetén. Ennek magyarázata, hogy így egy különböző, de pontos szakértőkből felépülő együttest kapunk. Ez a módszer természetesen egy nagyon leegyszerűsített alkalmazása a [12]-ben részletesen tárgyalt szakértő-együttes technikáinak. Azonban most nem lesz szükségünk arra, hogy különböző struktúrájú modellek döntéseit hogyan súlyozzuk az eredmény kialakításában, ugyanis azonos struktúráknál maradunk, melyek válaszait átlagolással aggreáljuk (implicite azt feltételezve, hogy az így előállított szakértők pontossága közel azonos). A KD lényege, hogy a fenti tapasztalat alapján a sokszereplős döntéshozást próbáljuk meg egy hálónak megtanítani. Az [1] módszere a következő: W (i) = train(x, f T=1 (, )) (2) ahol train(, ) a tanító operátor, melynek első argumentuma a tanító pontoknak és a hozzájuk tartozó elvárt kimeneteknek a halmaza (X), második argumentuma pedig a tanított neurális háló paraméteres leképezése. f T (, ) jelöli a T hőmérsékletű softmax aktivációt alkalmazó neurális hálót. Első paramétere a bemeneti minta, második paramétere a háló súlyai (W). d j = N 1 2N ft=t (x j, W (i) ) d j i=1 (3) d j az x j bemeneti vektorhoz rendelt soft-target, d j ugyanezen bemeneti mintához tartozó hard-target, N a szakértők száma, t pedig az alkalmazott hőmérséklet. W = train(x, f T=t (, )) ahol a X soft-targetekkel módosított tanító halmaz. A desztillált háló válasza: y(x) = f T=1 (x, W ) (5) A már hivatkozott [1]-ben végzett analízis alapján a módszer hatásosan alkalmazható a konstruált eszköz komplexitásának redukciójára minimális pontosságcsökkenés mellett. Nevezetesen a közölt értékek szerint a kiindulási modell 58.9%, míg a 10 db ilyenből álló szakértői együttes 61.1% pontossággal volt képes megjósolni a helyes osztályokat. A szakértői együttes tudását a kiindulási modellbe desztillálva pedig 60.8% pontosságot mértek, ami alig marad el a szakértői együttesétől. A magas hőmérséklet használata a soft-targetek gyártása és az ezt követő tanítás során azért fontos, hogy kiemeljük a hálók tudását, amit nem kódolnak az eredeti hard-targetek. Abban ugyanis nem különböznek a soft-targetek a hard-targetektől, hogy melyik kimeneten van a legmagasabb érték. Ez az egyes szakértők válaszától függetlenül is mindig teljesül (4)
9 a (3) összefüggés miatt. Amiben fontosabb különbség mutatkozik, az pont a többi érték. Ezek kisebb-nagyobb relációi azt fejezik ki, hogy az n db hálóból álló rendszer melyik oszályba sorolta volna második, harmadaik, stb helyen a képet. Soft-targeteket használva tehát nem csak azt tanulja a háló, hogy az adott képet melyik osztályba kellene sorolnia, hanem azt is, hogy melyekre hasonlít egy nagyon sok paraméterű, nagy pontosságú rendszer szerint. Ez által pedig implicite a többi osztályról is tudást szerez Felhasználási példa (Soft Decision Trees) Azt már láttuk, hogy a KD hogyan használható egy adott struktúrájú háló pontosságának növelésére a paraméterszám növekedése nélkül, arra pedig már több módszert is láttunk, hogy hogyan lehet kis pontosságvesztés mellett csökkenteni egy háló erőforrásigényét. A [2] egy olyan módszert tárgyal, amivel KD-t használva a CNN-eknél sokkal átláthatóbb, egészen más típusú modellt tanítunk. A Soft Decision Tree (enyhe döntési fa), a döntési fáknak egy olyan általánosabb modellje, melyben nem történik minden elágazásnál egyértelmű döntés, hogy merre kell menni, hanem minden lehetséges részfához hozzárendeljük az adott döntés valószínűségét (egy enyhe döntést hozunk). Ennek következtében a levelek közül nem pontosan egy adja a minta taksálását, hanem az osztályokba sorolás a levelekig kiszámolt valószínűségekből aggregálódik. [3]. A Soft Decision Tree rendelkezik a döntési fák átláthatóságával, ugyanis minden elágazásról (döntési helyzetről) eldönthető, hogy ott miről dönt éppen a modell. E közben rendelkezik a neurális hálók azon tulajdonságával is, hogy a végső döntést egy valószínűségi eloszlás alapján hozza meg. A [2] alapján, ezeket a tulajdonságokat felhasználva egy konvolúciós neurális háló tudása desztillálható Soft Decision Tree-be is. Az említett cikkben egy az MNIST adathalmazon 94.45%-os pontosságú Soft Decision Tree-t, és egy 99.21%-os pontosságot elérő CNN-t vettek alapul. A tudásdesztillálással tanított döntési fa pontossága elérte a 96.76%-ot. Így pontosabb modellt kapunk, mint az eredeti döntési fa és átláthatóbbat, mint az eredeti CNN.
10 Klasszikus paraméterredukció desztillálással Magasabb pontosságot nem csak szakértőegyüttesek alkalmazásával tudunk elérni, hanem nagyobb, így például mélyebb (több rétegű), szélesebb (rétegenként több neuront tartalmazó) vagy bonyolultabban kapcsolt rétegekből álló hálókkal is. Felmerülhet a kérdés, hogy van-e esélyünk egy nagy és komplex háló tudását egy kisebb, így kevesebb paraméterrel rendelkező, gyorsabban futtatható, jobban átlátható, egyszóval hatékonyabb hálónak átadni. Ennek értelme az lenne, hogy a probléma megoldására használhatnánk jól ismert és tesztelt, jó általánosítóképességű hálót, élesben pedig egy olyat, ami kis méretének következtében hatékonyan oldja meg a feladatot. A kettő problémát szétválasztva pedig oda jutunk, hogy a prototípus megoldás konstrukciója során nem kell azzal foglalkoznunk, hogy hatékonyan oldjuk meg a problémát. Erre elég akkor figyelni, amikor az éles rendszerbe kerülő hálót tervezzük. E hálónak két, egymásnak ellentmondó kritériumnak kell eleget tennie: 1. a nagy háló tudását még képes elfogadhatóan kis hibával modellezni, 2. maximálisan hatékony, tehát működése során a lehető legkevesebb erőforrást használja fel. InceptionV3 Méréseim alapján az 50 ezer tanítóképből és ezer validáló és teszt képből álló ClutteredMNIST adathalmaz problémájára a InceptionV3 [15] nevű, széles körben ismert konvolúciós neurális hálónak nem esik nehezére szinte tökéletesen rátanulnia. A tanításhoz a fine tuning technikát alkalmaztam, tehát egy más problémára betanult hálót úgy használtam fel, hogy annak utolsó néhány rétegét eldobtam és a helyükre saját, probléma specifikus részhálót konstruáltam, majd az egész hálót tanítottam. Ebben az esetben az 1000 osztályos imagenet problémára tanított hálót vettem a 10 osztályos számjegyfelismerési probléma alapjaként. Ehhez a Tensorflow és a Keras teljeskörű támogatást nyújt. A fine tuning eredményeképpen a háló a tanító adatokon 99.54%, a validáló adatokon 98,58%, a teszt adatokon 98,29% pontosságot ért el. A tanítás során minden réteg tanult, így több, mint 23 millió tanítandó paraméter volt a rendszerben. Ezeket a pontosságértékeket és a háló a paraméterszámát a dolgozat további részében viszonyítási alapként kezelem.
11 Tudás desztillálás példa Az M 1 háló struktúrája legyen a következő: 1. réteg: 2D konvolúció (ablakméret: 3x3, kimeneti csatornák száma: 32, aktiváció: relu) 2. réteg: maxpooling, (ablakméret: 2x2) 3. réteg: 2D konvolúció (ablakméret: 3x3, kimeneti csatornák száma: 32, aktiváció: relu) 4. réteg: maxpooling, (ablakméret: 2x2) 5. réteg: 2D konvolúció (ablakméret: 3x3, kimeneti csatornák száma: 32, aktiváció: relu) 6. réteg: maxpooling, (ablakméret: 2x2) 7. réteg: flatten 8. réteg: fully connected (neuronok száma: 10, aktiváció: softmax) A softmax hőmérséklettel való használatához a Keras nem nyújt alapértelmezetten támogatást, de ez szükség esetén könnyen megoldható, ha az (1) összefüggést két lépésre bontjuk a következőképpen: z = z T q i = e z j j (6) így a második lépést elvégzi a beépített softmax, az első lépés pedig implementálható Template rétegként. Az M 1 hálót szintén a ClutteredMNIST adathalmazon tanítva a konstruált hálók pontosságát (tudásdesztillálással és a nélkül) az 1.táblázatban foglalom össze: e z i M 1 M 1, KD T = 5 InceptionV3 tanító 60,43% 78,52% 99.54% validáló 58,42% 74,77% 98,58% tesztelő 58,43% 74,46% 98,29% 1. táblázat Az M 1 háló pontosságainak értéke, tudás desztillálással (középen) és a nélkül (bal) a tanító hálóhoz viszonyítva (jobb) M 1 háló tehát, ha nem is képes a maga 39 ezer paraméterével tökéletesen leutánozni az InceptionV3 teljesítményét, de láthatóan sokkal jobb eredményt tudunk elérni, ha a tanításhoz tudásdesztillálást használunk.
12 Redundáns szűrők eliminálása A továbbiakban olyan tulajdonságait tárgyalom a konvolúciós neurális hálóknak, amelyek két megvizsgálandó szempont alapján hatékonyságcsökkentést okoznak, és ezek kiváltására próbálok meg megoldást tanácsolni. Ez a két szempont a következő: 1. megnövekedett erőforrásigényhez vezető tulajdonságok, 2. a háló döntésének magyarázhatóságát rontó tulajdonságok. Az első vizsgálati szempont magától értetődő, hiszen az minden informatikai rendszer célja, hogy erőforrásainkat minél hatékonyabban kihasználjuk, ezáltal csökkentve a számítási idő, memória és egyéb erőforrások igényét. A második szempont absztraktabb, ugyanis (a tudomány jelenlegi állása szerint) kvalitatívan nem mérhető. A komplexitás növekedése alapvető velejárója a neurális paradigmának. Minél mélyebb és ez által komplexebb egy neurális háló, annál bonyolultabb leképezések (minták alapján történő) megtanulására alkalmas, melyeket a hagyományos matematikai modellekkel a szakértők nem voltak képesek feltárni. Ez maga után vonja a konstruált háló döntésének nehezebb magyarázhatóságát. Éppen ezért a komplexitás növelés nem célunk, maximum elfogadjuk, ha nem látunk módot hasonló eredmény elérésére kevésbé összetett módszerek alkalmazásával. Az AlexNet [13] volt az első mély, képfelismerési problémákhoz konstruált konvolúciós neurális háló. Bár az azóta megjelent megoldások (VGG, GoogleNet, ResNet, FractalNet, stb.) nagyobb pontosságú megoldásokat, esetleg hatékonyabb erőforrás kihasználást biztosítanak, mind a mai napig ez a szakirodalomban az egyik legtöbbet vizsgált [16, 17, 18] CNN. Ez annak köszönhető, hogy publikálása fontos szerepet játszott a neurális paradigma újra élesztésében és széles körű elterjedésében. Ahogy a háló alap publikációjának [13] szerzői is írják cikkükben, az áttöréshez szükség volt a GPU-k fejlődésére, az ezekre optimalizált hatékony 2D konvolúció implementációkra, valamint olyan nagy és diverz adathalmazokra, mint az ImageNet. 3. ábra Az ábra a [13] cikkből származik annak 6. oldalán Figure 3 néven található AlexNet első konvolúciós rétegének 96 db 11x11x3-mas konvolóciós kernele látható rajta. Az AlexNet első rétegének konvolúciós szűrőit vizualizálja a 3. ábra (forrás [13]). Könnyen észrevehető, hogy az ábra felső három sorában lévő kernelek érzéketlenek a színekre, míg az alsó háromban lévők többnyire nem. Két másik szembetűnő tulajdonsága is felfedezhető
13 a taglalt filtereknek, melyek általánosan is megfigyelhetőek a CNN-ekben. Egyrészt látható, hogy vannak a megtanultak között szinte minden elemében nulla (a képen teljesen egyenletesen szürke) kernelek. Másrészt vannak olyan kernelek, melyek egymástól szinte egyáltalán nem különböznek. A szinte csupa nullákból álló szűrés pedig azt jelenti, hogy itt a hálónak nem sikerült semmi értelmes jellemző kiemelését megtanulnia. Ugyanis egy csupa nullásokból álló kernellel való konvolúciónak az eredménye szintén csupa nullákból álló kimenet lesz. Ez pedig az előzőhöz hasonló megfontolásból pazarló, hiszen ha ezeket a paramétereket is sikerült volna rendesen beállítani, akkor talán nőhetne a háló pontossága. Az ilyen szűrések jelentőségével a 4.2 alfejezetben külön foglalkozom. 4.1 Geometriai torzítások Általános tapasztalat a konvolúciós neurális hálókkal kapcsolatban, hogy bizonyos, az emberi döntéshozatalt egyáltalán nem befolyásoló, bemeneti képeket terhelő változtatásokra a háló nem az elvárt módon reagál. Itt most nem a szintén nagy problémát jelentő és a szakirodalomban is részletesen tárgyalt Adversial Attack [5] problémára utalok, hanem olyan módosításokra, mint a megvilágítás, a képen lévő tárgy színének megváltoztatása, eltolások, forgatások, átskálázás. Míg egy ember számára egyformán nehéz megmondani, hogy milyen fajtájú kutya látható egy képen, akár természetes, akár mesterséges fényben készült az, és ugyanígy, ha a kép egészét, vagy csak negyedét foglalja el. Ugyanezt a viselkedést a CNN-ektől is joggal várjuk el. Ez elérhető, ha megfelelően diverz mintahalmazzal történik a hálók konstruálása, melynek egyik lehetséges módja a minták augmentációja. Általános tapasztalat, hogy az egyes objektumok előfordulásának tanítómintákban látható sokféleségét a hálók redundáns szűrések megtanulásával kezelik [13]. Bár a jelenség robosztusság szempontjából akár előnyös is lehet (pl. Dropout esete), viszont mind interpretálhatóság, mind számítási erőforrásigény szempontjából előnytelen, hiszen az egymással pl. kis mértékű elforgatás, skálázás miatt jelentősen korreláló szűrőkkel történő konvolúciók eredménye is jelentősen korrelál. Ez a jelenség megfigyelhető az AlexNet szűrőiben is (3. ábra). Többek között ezzel a kérdéssel is foglalkozik a [22], melyben egy teljesen új típusú neurális háló struktúrát vezetnek be. A cikk által javasolt kapszula háló ismertetése a dolgozat szempontjából kevésbé fontos, mint motivációinak bemutatása. 4. ábra Egy konvolóciós neurális háló számára a két kép hasonló, mivel hasonló részleteket tartalmaznak. (forrás [19])
14 A kapszula hálók konstrukciójának főbb motivációja az invariáns viselkedés ekvivariánsra cserélése. Ez alatt azt kell érteni, hogy egy komplexebb objektumot (például emberi arcot) felépítő egyszerűbb objektumok megjelenésének állapota (pl. skála, orientáció stb.) között ekvivalencia kell, hogy fennálljon annak érdekében, hogy valóban a kompozit objektumot lássuk. Ennek ellenőrzését a klasszikus, redundáns szűréseket és azokat követő maxpooling-ot tartalmazó hálózatok nem teszik lehetővé (kiváltképp azért nem, mert ritkák azok a tanítóminták, melyek e miatt okoznának fals osztályozást). A probléma viszont nem jelentkezne, ha a detektálandó objektumunk uniformizált állapotban jelenne meg a háló bemenetén (ez alatt egy regisztrált állapotot értve), mely hatására az egyes rész objektumok is egymással konzisztens állapotban jelennének meg. Ilyen értelemben javulna a háló interpretálhatósága, csökkenne a számítási erőforrásigénye, valamint a robosztussága is javulna Uniformizálás A fentiekben ismertetett problémákra alternatív megoldásként kínálkozik a bemeneti képek uniformizálása. Klasszikus, szakértői képfeldolgozó rendszerek esetén is szinte mindig szerepel az első lépések között a képek valamilyen értelemben uniform állapotra hozása. Ez legtágabb értelemben véve egy olyan előfeldolgozása a bemeneti képeknek, mely során a hasonló objektumokhoz hasonló megjelenési állapotot rendelünk (ez értelmezhető akár a priori tudás hozzáadásaként is), ez után adjuk a hálónak a képet feldolgozásra. Konkrét példaképpen pedig előre megpróbáljuk meghatározni a felismerendő objektum méretét, orientációját és csak ez után kerül a kép a hálóhoz, ami megpróbálja felismerni. Elsőként, csak az objektumok méretének problémájával foglalkozva, megpróbáltam bizonyosságot szerezni arról, hogy ha csak hasonló méretű objektumokat tartalmazó képek képezik a CNN bemenetét, akkor kisebb háló is elég ugyanolyan pontosság eléréséhez. A dolog proof-of-concept jellege miatt nem fordítottam hangsúlyt a skálakompenzáció automatizálására. 5. ábra A DoG függvényt használó algoritmus eredménye egy olyan képen, amin a felismerendő objektum egy blob (bal) és egy olyanon melyen nem (jobb).
15 A blob detektálás jól ismert algoritmus a klasszikus képfeldolgozásban. A blob definíció szerint egy világos folt egy sötét képen, vagy egy sötét folt egy világoson, aminek megtalálásához az algoritmus különleges szűréseket használ. Ezen szűrések alapjául a Laplacian of Gaussian (LoG), a Difference of Gaussian (DoG) vagy a Determinant of Hessian (DoH) függvény szolgálhat. Bármelyiket választva, azt az origó körül megforgatni, majd mintavételezni kell. Az így kapott szűrőt megfelelően minden iterációban átméretezve megtalálhatók egy képen a blobok. Az ideális esetet szemlélteti a 5.ábra bal, és egy kevésbé ideálisat a jobb oldala. A legegyszerűbb konvolúciós háló, amit megvizsgáltam két konvolúciós rétegből állt. Egyenként 3 illetve 4 kimeneti csatornával, 9x9-es szűrésekkel. Mindkét konvolúciós réteget relu aktiváció és 2D averagepooling követett. A flatten réteg után egy 10 neuronos fully connected réteg, relu aktivációval, majd a két neuronos kimeneti réteg softmax aktivációval. Az elért pontosságok: 97,3% a tanító, 82,3% a validáló és 75,0% a teszt adatokon. Ami azt jelenti, hogy a 80 teszt kép közül 60-at felismert a háló. Ez az eredmény arra engedett következtetni, hogy a képek skálafüggetlenítése mindenképp jó irány, ha hatékony osztályozási feladatokat végző CNN-eket akarunk konstruálni Uniformizálás neurális hálóval A Spatial Transformer Network (STN) [4] egy olyan konvolúciós neurális hálózat, ami regresszióval becsli a merev regisztráció paramétereit. Ehhez tanulás során felhasználja a minták cimkézését ami alapján tanulja a regisztáció paramétereit, mely értékeket direktben a tanítás során nem kap meg. Ez alapján vizsgálódásom szempontjából több előnyös tulajdonsággal is rendelkezik. Először is a regisztráció a klasszikus képfeldolgoásban az a lépés ami a különböző nézőpontokból készült képeket egy közös koordinátarendszerbe transzformálja. A közös koordinátarendszer pedig eltolás, skálázás és forgatás tekintetében uniformizálás. Másodszor, mivel ezt az STN cimkézés alapján tanuja, a képen található objektum alapján különbözően lesznek regisztrálva a képek, a targettől függően. Továbbá, mivel teljesen differenciálható leképezést megvalósító CNN alapú a technológia, ennek köszönhetően önálló rétegként beilleszthető bármely CNN elejére, vagy akár két réteg közé, így az uniformiázáls tanulása együtt történhet az osztályozási probléma tanulásával. Az STN három fő részből áll: egy regressziós modell, ami a képen elvégzendő affin transzfomáció 6 paraméterét becsli egy mintavételező rács, aminek segítségével az affin transzformációt elvégezzük a képen, és végül egy differenciálható mintavételezési lépés. A mintavételezésnek, azért kell differenciálhatónak lennie, hogy a kimeneti hibája is visszaterjeszthető legyen, egy felelől az STN regressziós modelljének, másfelől, ha az STN előtt is rétegeknek.
16 A regressziós modell lehet bármilyen neurális háló alapú megoldás. Az általam használt (a továbbiakban STN rétegként hivatkozott) modell a következő volt: 1. réteg: maxpooling (ablakméret: 2x2) 2. réteg: 2D konvolúció (ablakméret: 5x5, kimeneti csatornák száma: 20) 3. réteg: maxpooling (ablakméret: 2x2) 4. réteg: 2D konvolúció (ablakméret: 5x5, kimeneti csatornák száma: 20) 5. réteg: flatten 6. réteg: fully connected (neuronok száma: 50, aktiváció: relu) 7. réteg: fully connected (neuronok száma: 6) A regressziós modellt bilineáris interpoláció követi. Így ha egy rétegként tekintünk az előbb részletezett 7 rétegre és az interpolációra, akkor egy olyan réteget kapunk, ami a bemeneti képen egy affin transzformációt és egy mintavételezést végez a réteg kimeneti hibájának minimalizálása érdekében. Méréseim során az STN minden esetben a legelső rétege volt a hálónak. Ennek magyarázata, hogy így az STN kiementét bementként kapó konvolúciós szűrések már nem kell, hogy feleslegesen redundánsak legyenek. A ClutteredMNIST adathalmazból származó 60x60 pixeles bemeneti képen minden esetben 30x30-as mintavételező rácsot alkalmaztam, bilineáris intepolációval. A továbbiakban a regressziós modell hatékonyságának növelése nem volt cél, mivel paraméterszámban nem jelentős, és a kimenete könnyen értelmezhető, így interpretálhatóság szempontjából is kvalitatíve hatékonynak minősül Tapasztalati eredmények Elsőként az alábbi háló architektúrát vizsgáltam: 0. réteg: STN réteg (kimeneti kép: 30x30, bilineáris interpoláció) 1. réteg: 2D konvolúció (ablakméret: 3x3, kimeneti csatornák száma: 32, aktiváció: relu) 2. réteg: maxpooling, (ablakméret: 2x2) 3. réteg: 2D konvolúció (ablakméret: 3x3, kimeneti csatornák száma: 32, aktiváció: relu) 4. réteg: maxpooling, (ablakméret: 2x2) 5. réteg: flatten 6. réteg: fully connected (neuronok száma: 256, aktiváció: relu) 7. réteg: fully connected (neuronok száma: 10, aktiváció: softmax) A ClutteredMNIST adathalmzon a tanítás után kapott pontosság értékek a tanító képeken 97,66%, a validáló és a teszt képeken pedig 95,4%. Figyelembe véve, hogy ugyanezen probléma esetén az Inception V3 alapú megoldás pontossága mindkét esetben kevesebb, mint 3%-al haladja meg a vizsgált háló pontosságát, míg a paraméterek számában nagyságrendileg 50-szeres az eltérés, bizonyossá vált az uniformizálás hatásossága. Első észrevételem, hogy előzetes várakozásaimmal ellentétben az InceptionV3 tudásának desztillálásával nem kaptam szignifikánsan pontosabb modellt. Ehhez persze az is hozzájárul, hogy a modell már eleve nagyon pontos és szignifikáns különbség kimérésére nincs is érdemben lehetőség. Az ezzel kapcsolatos méréseim eredményét a 2.táblázatban foglalom össze.
17 hard target soft target T=1 s.t. T=2 s.t. T=5 s.t. T=10 Incept.V3 tanító 97, 66% 97,30% 97,09% 98,41% 98,01% 99.54% validáló 95, 40% 94,89% 95,14% 95,66% 94,75% 98,58% tesztelő 95, 41% 95,07% 95,06% 95,14% 94,69% 98,29% 2. táblázat A vizsgált háló pontossága a cluttered MNIST adathalmazon különböző hőmérséklet értékek használatával. A továbbiakban az STN réteg hatákonyságával kapcsolatban végeztem méréseket, miközben az utána következő rétegek architektúráját módosítottam. Először is a 6. réteget elhagytam. Ez hatékonyság szempontjából fontos lépés lehet, úgyanis egy részről ennek a rétegnek az elhagyásával az háló paramétereinek a száma ről re csökkent, másrészről pedig minél kevesebb fully connetced réteget tartalmaz egy neurális háló, annál egyszerűbb a döntéseinek magyarázata. Az ezzel a módoítással végzett méréseim eredménye a 3.táblázatban látható. Az első oszlopból leolvasható, hogy a réteg elhagyásával a háló pontossága nem romlott drasztikusan. Validáló és tesztelő képek esetében valamivel több, mint 2% a romlás. A tanító adatokon ennél kicsit több, de ez azzal magyarázható, hogy a fully connected réteg több paramétere révén hajlamosabbá teszi a hálót a túltanulásra, így ez a kicsit nagyobb százalékos romlás nem írható egyértelműen a veszteségek közé. hard target soft target T=1 s.t. T=2 s.t. T=5 s.t. T=10 Incept.V3 tanító 94, 45% 94,53% 95,29% 94,44% 93,96% 99.54% validáló 93, 17% 92,94% 93,28% 91,18% 90,43% 98,58% tesztelő 93, 01% 93,05% 92,82% 91,53% 90,57% 98,29% 3. táblázat Az utolsó előtti fully connected layer elhagyásával kapott háló pontossága különböző hőmérséklet értékek használatával. Ez után az STN utáni maxpooling rétegeket cseréltem averagepooling rétegekre. Ennek a lépésnek a magyarázata a [22] alapján az, hogy a maxpooling rétegek egymás után többszöri alkalmazása érzéketlenné teszi a hálót az objektum részeinek egymáshoz viszonyított helyzetére és méretére, mivel ezek kimenete a régió egyetlen pixelétől függ csak. Ez persze javarészt nem jelentkezik, ha uniformizált a bemenet, hiszen ilyen esetekben a réteg bemenete nem elegendően diverz a nem kívánt invariancia kialakulásához. A csere hatására a háló tanulandó paramétereinek a száma természetesen nem változott. Ez a változtatás ismét kicsit több, mint 2% romlást okozott a háló validáló és tesztelő pontosságában. Látszik azonban az is, hogy ez a lépés csak a háló általánosítóképességét rontotta, a tanító adatokon a háló az előző mért értéknél még jobban is teljesített.
18 hard target soft target T=1 s.t. T=2 s.t. T=5 s.t. T=10 Incept.V3 tanító 95, 35% 95,29% 94,20% 93,41% 92,80% 99.54% validáló 91, 52% 91,11% 90,45% 88,65% 87,69% 98,58% tesztelő 91, 28% 91,18% 90,34% 88,23% 88,01% 98,29% 4. táblázat A maxpoolingok avaragepoolingra cserélésével kapott háló pontossága különböző hőmérséklet értékek használatával. Az sajnos világosan látszik a 2., 3., 4. táblázatokból, hogy a tudás desztillálás módszere nem csak az első esetben tapasztalt túl közeli eredmény miatt nem működik. Az egyre rosszabb eredmények feltevésem szerint azzal magyarázhatóak, hogy mint ahogy azt fentebb már taglaltam a desztillálás módszerével a háló azt tudja megtanulni egy másik hálótól, hogy mely osztályok mintái mutatnak jelentős hasonlóságot Ennek a tudásnak a kihasználásához viszont az kell, hogy a két háló ugyanazon eloszlásból származó mintákat lásson. Mivel az STN réteg struktúrája miatt az azonos osztályba tartozó minták uniformizálására törekszik, míg ennek megfelelő transzformációkat nem végez az InceptionV3 alapú megoldás, ezért hasznos plussz információt nem tud szolgáltatni a vizsgált esetekben. Viszont a háló pontossága két nehezen interpretálható rétegnek az eldobása után (melyek közül az egyik paraméterszámban önmagában is nagyobb, volt, mint az így kapott háló) még mindig 90% felett tartható. Ez markánsan alátámasztja a háló növekvő hatékonyságát a képek uniformizálása következtében. Már csak az a kérdés, hogy még kevesebb réteg alkalmazásával megtartható-e a háló válaszának nagy pontossága. A két 3x3 konvolúciós réteget megpróbálhatjuk eggyel kiváltani. Melyhez az kell, hogy az új réteg egy pixelének érzékenységi mezője legalább akkora legyen, mint az eddigi két konvolúciós rétegé. Ehhez egy 9x9 méretű kernel használata elegendő, mivel a második konvolúciós réteg kimenetének egy pixelének az értéke a bemenetének 3x3 pixelétől függ. Ennek a 3x3-mas résznek az előállításához az averagepooling egy 6x6 pixelnyi területet dolgozott fel. Amely pixelek pedig az első konvolúciós réteg kimenetén jelennek meg, úgy, hogy ezek értéke a bemenet 8x8 pixelétől függ. Mivel általában nem alakalmazunk páros méretű konvolúciós szűrőket, ezért 9x9 méretű kernelt használtam. Azért, hogy a kimenet se legyen nagyobb dimenziójú, mint a korábbi két réteg kimenete 2x2 strideot is alkalmaztam. Az így kapott réteg által modellezhető leképezések halmaza nem áll egyértelmű relációban az eredeti két réteg által megvalósítható leképezések halmazával. Ezen kívül a Relu aktivációt LeakyRelura cseréltem, mert ez egy invertálható nem linearitás, ami elősegítheti a háló döntésének interpretációját. Fontos megjegyezni, hogy az által, hogy csak egy konvolúciós réteget alkamazok, az ezen réteg beli szűrők definíciója alapján direkt vizuálisan interpretálhatóvá válik a háló általános döntéshozatala.
19 Az így konstruált háló tehát : 0. réteg: STN réteg (kimeneti kép: 30x30, bilineáris interpoláció) 1. réteg: 2D konvolúció (ablakméret: 9x9, kimeneti csatornák száma: 32, aktiváció: leakyrelu) 2.réteg: averagepooling, (ablakméret: 9x9) 3.réteg: flatten 4.réteg: fully connected (neuronok száma: 10, aktiváció: softmax) A paraméterszáma , ami a kiindulási modell paraméterszámának csaknem negyede. A tanítással elért pontosság pedig a tanító képekre 93, 73%, a validáló és teszt képekre pedig 89, 14%, illetve 89, 53%. Ez az eredmény egy kicsit elmarad a kitűzött 90%-tól, viszont tovább javítható, ha a konvolúciós rétegnek több kimeneti csatornája van. A kívánt pontosság már 47 csatorna használatával előáll, de tovább növelhető, még több csatorna használatával. Azonban tetszőlegesen sok csatornát sem érdemes tetszőlegesen sok csatornát alkalmaznunk, hiszen az egyre több és több csatornának egyre kevesebb a pontossághoz hozzáadott értéke, ez pedig hatékonyságcsökkenéshez vezet. Továbbá ronthatja a háló általánosító képességét is. Az így konstruált háló pontosságának alakulását a csatornák számának a függvényében az 5. táblázatban foglalom össze. csatorna szám tanító 93,73% 96, 02% 96,39% 94,56% 96,71% 96,31% validáló 89,14% 90, 33% 90,82% 90,45% 91,61% 92,38% tesztelő 89,53% 90, 26% 91,30% 90,54% 92,02% 92,70% paraméterszám 110, , , , , , táblázat Az egy konvolúciós réteget tartalmazó háló pontossága a konvolúciós réteg kimeneti csatornaszámának függvényében Összefoglalás Ebben a fejezetben tahát rámutattam az uniformizálás jelentőségére a konvolúciós neurális hálók esetében. Ez után először proof-of-concept jellegel a blobdetektáló algoritmust használva, majd a neurális háló alapú Spatial Transformer Networkot alkalmazéséval be is bizonyítottam, hogy szignifikánsan hatékonyabb hálózatok tervezhetőek ilyen módon. Majd pedig interpretálhatósági megfontolások mentén tovább egyszerűsítettem a háló struktúráját, minek hatására az STN után egyetlen konvolúciós és szintén csupán egy darab fully connected rétegből álló hálóval is sikerült a pontosságot a tanító, validáló és tesztelő adatokon is 90% felett tartani. Fontosnak tartom még kiemelni, hogy az STN-nek ugyanúgy diverz tanítóadatokra van szüksége, hogy igazán jól alkalmazható legyen. Használatával viszont a hálónak egy a többitől jól elválasztható része foglalkozik a skálázás, eltolás, forgatás kérdésével, így (mérésekkel is alátámasztva) biztosabbak lehetünk benne, hogy ezekből nem származik redundancia. Ennek hatására a háló komplexitása jelentősen csökken, továbbá a döntéshozatal értelmezése is jelentősen egyszerűsödik, hiszen kevesebb és kevésbé korrelált szűrések sorozatának függvénye a bemeneti minta taksálása.
20 4.2 Háló tanítása L0 regularizációval Az előző fejezet végére sikerült egy meglehetősen sekély hálózatot létrehozni, melynek hibája bár folyamatosan nőtt az egyszerűsítések mentén, sikerült azt racionális kereteken belül tartani. Arra is rámutattam, hogy a pontosság növelhető, ha szélességét növeljük. Ebben a fejezetben arra teszek ajánlást, hogy hogyan lehet ezt is hatásosan megvalósítani. A javasolt módszer általánosan alkalmazható CNN-ek hatékonyabbá tételére Motiváció Általánosan alkalmazott módszer CNN tervezéskor, hogy a bemenettől távolodva egyre több kimeneti csatornával rendelkezzenek a konvolúciós rétegek (miközben az egyes csatornák felbontása monoton csökken). Az InceptionV3 például az általam használt konstrukciójában 2048db 3x3 méterű csatornát állít elő a bemeneti képből a döntéshozáshoz, a [6]-ban bemutatott 34 rétegű ResNet pedig 512db 3x3 méretűt. A sok csatorna azért szükséges, hogy minél többféle szűrésen, jellemző kiemelésen menjen keresztül a kép (ezáltal növelve a háló által approximálható nemlineáris leképezések halmazát). Az előző fejezet végén méréssel is alátámasztottam, hogy minél több csatornából áll az utolsó konvolúciós réteg kimenete, annál nagyobb pontosságot lehet elérni. Azonban ez a módszer is hatékonyságcsökkenéssel jár mindkét vizsgált szempont szerint. Először is bár a paraméterszám növekedés nem drasztikus (az 5. táblázatban látható konkrét példában 572-vel nő a tanulandó paraméterek száma minden új csatornával) a konvolúciós műveletek elvégzése teszi ki a CNN-ek számítási idejének nagy részét. Az interpretálhatóság pedig az által nehezedik, hogy minden kimeneti neuron az összes csatornától függ. Indokolt tehát a tanítás közben a hálót arra késztetni, hogy csak a döntéshozás szempontjából szükséges konvolúciókat végezze el és csak az adott neuron szempontjából szükséges csatornákat vegye figyelembe. A alfejezetben már röviden ismertettem paraméter nyesést végző módszereket. A [9]-ben javasolt eljárás súlyonként végez vágást a kimenetre gyakorolt hatást minimalizálva. A [10] algoritmus pedig a hasonló súlymátrixszal rendelkező neuronokat vonja össze. Ezen módszerek hátránya, hogy a tanítás során nem cél a vágás elősegítése Regularizáció Felügyelt tanulás minden esetében egy jól definiált célfüggvény minimalizálására törekszünk: arg min {C(W) } W (7) C a tanítás során minimalizálandó célfüggvény, W pedig a neurális háló súlyait tartalmazó tenzor, melyet a későbbiekben három változóval indexelünk, és minden (l) eleme egy 2D mátrix (W i,j jelöli az l. réteg i. csatornája és az l. réteg j. csatornája közötti szűrő súlymátrixát). Ez a célfüggvény legegyszerűbb esetben (tisztán frekventista megközelítés) a predikciók hibájának összege, ahol a hiba kiszámítása szintén előre meghatározott módon, a targetek függvényében történik: C(W) = l(f(x i, W), d i ) i (8)
21 ahol l a veszteségfüggvény, f(x i, W) a háló kimenete x i bemenetre W súlyok mellett, d i pedig az x i -hez tartozó target. Regularizáció során a célfüggvényt kiegészítjük egy büntető függvénnyel is. Ezért a minimalizálás hatására a W a büntetőfüggvény által impliciten meghatározott tulajdonságokkal fog rendelkezni (és ezzel áttérünk a Bayes-i paraméterbecslésre). Általánosan regularizáció esetén a minimalizálandó összefüggés: C(W) = l(f(x i, W), d i ) i + ρ H(W) (9) ahol ρ hiperparaméter, H pedig a regularizációs büntetőfüggvény. A továbbiakban az első tagot likelihood tagnak hívom. Először vizsgáljuk meg, hogy mik az ismertebb büntetőfüggvények. A Tikhonov regularizációnak is nevezett L 2 2 (L 2 norma négyzet): L 2 2 H(W) = W (l) i,j (u, v) 2 l,i,j (10) Az összefüggés alapján látható, hogy a célfüggvényhez hozzáadjuk a háló súlyainak négyzetösszegét, ennek hatására a tanítás során arra bíztatjuk a hálót, hogy minél kisebbek legyenek a súlyok. Széleskörűen alkalmazott regularizácó a neurális hálók tanítása során, belátható, hogy a korai leállás, illetve a neuronok kimenetének zajjal történő terhelése is hasonló jellegű regularizáció. Érdemes megjegyezni, hogy a szakzsargonba hibásan ezt nevezik L 2 regularizációnak. Mivel a későbbiekben azon módszert is vizsgálni fogom, ezért én itt nem azt az elnevezést használom. Az L 1 büntetőfüggvényes regularizáció során a súlyok négyzetösszege helyett az abszolútértékük adódik hozzá a célfüggvényhez. u,v L 1 H(W) = W (l) i,j (u, v) l,i,j (11) Így az L 2 2 -nél relatíve kevésbé bünteti a nagyobb súlyokat, azonban a kisebbeket jobban. Könnyen belátható, hogy általános esetben ez a ritkasági regularizációt legkisebb hibával közelítő konvex büntetőfüggvény. Alkalmazása során a háló motiváltabb, hogy a kisebb amplitúdójú, ezért irrelevánsnak tűnő súlyokat teljesen kinullázza, miközben kevésbé érzékeny a nagy súlyokra. Szintén gyakran alkalmazott és a DeepLearning keretrendszerek által is támogatott regularizációs típus. Az L 0 norma alapú ritkasági regularizációt főleg jelfeldolgozásban alkalmazzuk, de létezik gépi tanulásos megfelelője is (pl. az adaptive Lasso [20]): u,v L 0 H(W) = 1 δ (W (l) i,j (u, v)) l,i,j u,v (12)
22 δ a jelfeldolgozásból ismert Kronecker delta függvény tehát: 1 ha x = 0 δ(x) = { 0 egyébként (13) Az L 0 regularizáció során tehát a célfüggvényhez a W nem nulla elemeinek a számát adjuk hozzá. Ez az L 1 -hez hasonló viselkedést eredményez, azt hozzátéve, hogy kicsi és nagy nem 0 elemekre azonos a büntetés, ennek köszönhetően nem érzékeny a súlyok amplitudójára. L 0 regularizációt szokás szerint nem alkalmazunk neurális hálók tanítása során. Ennek oka, hogy egyrészt nem konvex, másrészt minden pontjában, ahol deriválható, 0 a derivált értéke., A széles körűen alkalmazott gradient descent (és az erre épülő klasszikus eljárások, pl. momentumos gradiens, adaptív gradiens módszerek) a C célfüggvény minimalizálása során csak korlátolt mértékben képesek a regularizációs büntetőfüggvény minimalizálására. A fenti regularizációk mind egyesével büntetik a súlyokat (a hozzájuk kapcsolódó minimalizálási problémák teljesen szeparábilisek), így hatásuk is súlyonként érvényesül. Ezzel szemben a következő regularizációk a súlyok egy csoportját bünteti. Az L 2 regularizáció mátrixokon értelmezett analógiája: a Frobenius-norma definíciója pedig: (l) L F H(W) = W i,j F l,i,j (14) (l) W i,j F = (W (l) 2 i,j (u, v)) u,v (15) Tehát így konvolúciós kernelenként adódik hiba a célfüggvényhez, ami a később részletezett okokból előnyös. A fent ismert regularizációs módszerek után definiáljuk Tenzor L 0 néven a következő büntető függvényt: Tenzor L 0 H(W) = 1 δ ( W (l) i,j ) F (16) Ennek az új regularizációnak a hatása az L F -éhez lesz hasonló abban a tekintetben, hogy súlyok egy csoportját bünteti és L 0 -éhoz abban a tekintetben, hogy a nem csupa 0 súlymátrixok száma jelenik meg a büntetőfüggvényben. Ezzel tehát a két viselkedést ötvözve arra sarkalljuk a hálót, hogy a tanítás során minél kevesebb nem 0 csupa súlymátrix keletkezzen. Három kérdés merül fel ezen a ponton. Az első kérdés, hogy miért akarunk súlyokat csoportonként regularizálni. Erre a következő fejezetben adom meg a választ. A második kérdés, hogy mit érünk egy olyan neurális hálóval, amit a tanítás során rávettünk arra, hogy minden súlymátrixa csupa 0 tagokból álljon. Erre a válasz az, hogy patológiás esetek kivételével nem állhat elő, hogy minden mátrix csupa 0 tagú legyen. Az összes büntető tag csupán, mint plusz megkötés jelentkezik a frekventista (8) összefüggés mellett és a ρ l,i,j
23 hiperparaméterrel tudjuk szabályozni, hogy ennek a hatása mennyire markánsan érvényesüljön. Ha tehát egy súly mátrix kinullázása nagyobb hibát okoz a likelihood tagban, mint amennyit javít a büntető tagon, akkor nem fog változni. A harmadik kérdés, hogy miként tudjuk érvényre juttatni a Tenzor L 0 regularizáció hatását, ha tudjuk, hogy ennek is, mint az L 0 -nak 0 a deriváltja minden pontban (a 0 pontot leszámítva, ahol pedig nem deriválható), tehát a C célfüggvény gradiensében nem jelenik meg ettől függő tag. Erre megoldást adhat a proximity gradient módszer melynek segítségével iteratívan tudjuk közelíteni a büntető függvénnyel sújtott célfüggvény egy kritikus pontját. A gradient descent algoritmus a minimumhelyet a következő összefüggés alapján számolja iteratívan: = W (t) μ C(W) (17) ahol az eddigi jelöléstől eltérően W (t) a mátrix súlyait tartalmazó tenzor, az algoritmus t. iterációja után, μ pedig hiperparaméter, az úgynevezett bátorsági faktor. W (t+1) Proximal gradiens módszer használata esetén a súlytenzor frissítése két lépésre bontható a következő módon: W = W (t) μ W l(f(x i, W), d i ) W (t+1) i = prox ρ,h (W ) Az első lépés tehát azonos a korábban látottal, majd alkalmazzuk a proximity operátort: (18) prox ρ,h (W ) = arg min W {1 μ W W ρ H(W) } A korábbi definícióba (15) behelyettesítve: W W 2 2 = (W (l) i,j (u, v) W (l) i,j (u, v)) 2 l,i,j,u,v (20) Ez a tag tehát úgy interpretálható, hogy a W minél kisebb mértékű megváltoztatása mellett szeretnénk érvényre juttatni a büntető tagot, melyet a különböző regularizációk esetén a következőképpen írhatunk fel: (ismét visszatérek arra a jelölésre mikor, a felső index a réteg sorszáma.) L 2 2 W (l) i,j (u, v) = W (l) i,j (u, v) (1 + ρ 2μ ) = W (l) i,j (u, v) α (21) α hiperparaméter csak ρ-tól függ, így az önálló hiperparaméterként hangolható. Látható, hogy a büntető tag multiplikatívan csökkenteni a súlyok értékét, így nagyobb mértékben redukálja a nagyobb súlyokat. (19)
24 L 1 W (l) i,j (u, v) = max {0, W (l) i,j (u, v) ρ 2μ } sign{w (l) i,j } (22) A súlyokat additívan csökkenti, így a (11) összefüggéssel analóg módon kevésbé érzékeny a nagyobb abszolút értékű súlyokra. Ezt a műveletet hívja a szakzsargon zsugorításnak. A folyamatos csökkentés ismét csak azért nem vezet csupa 0 súlyokkal rendelkező hálóhoz (egyik esetben sem), mert az első lépés hatása erőteljesebb azon súlyok esetén, melyek eldobása túl nagy hibát eredményezne (a likelihood tag hatása miatt megmaradnak). L 0 W (l) i,j (u, v) = { W i,j 0 ha W (l) i,j (u, v) < ρμ (l) (u, v) egyébként (23) Az L 0 regularizáció a küszöbértéknél kisebb súlyokat kinullázza, minden iterációban, tehát a (12) összefüggéssel analóg módon a nem 0 elemek számát csökkenti. Az L 2 regularizáció proximity operátorában megjelenik a mátrix (vektorok euklideszi hosszával analóg) Frobenius-normája (melyet β jelöl): (l+1) (l+1) (l+1) ρ (l) (W L 2 W i,j = { i,j β i,j ) β i,j (1 2μ ) ha β (l+1) ρ i,j 2μ 0 egyébként (24) tehát bár kinézetre valóban hasonlít az L 2 2 -re, viszont az eljárás csak a súlymátrixok Frobenius-normáját zsugorítja, az egyes súlyok egymáshoz viszonyított értékét nem módosítja. Ezáltal teljes mátrixok kinullázására törekszik az egyes súlyok kinullázása helyett. Végül a Tenzor L 0 regularizáció proximity operátorát ismét az L 0 és az L 2 proximity operátorok kombinációjaként kapjuk: 0 ha W (l+1) (l) i,j F < ρμ Tenzor L 0 W i,j = { egyébként W (l) i,j (25) Tehát ha a mátrix Frobenius-normája a küszöb alatt van, akkor az egész mátrixot kinullázza, ellenkező esetben nem módosítja. Az összefüggésből látható, hogy itt nincs semmilyen zsugorító hatás, ezért bár mérsékelten, de megmarad ugyanaz a probléma, mint ami a gradient descent alapú L 0 minimalizációnál jelentkezett. Ezen az iteratívan újrasúlyozott L 2 norma alapú megoldás segíthet [21], mely az L 0 normás minimalizációt iteratívan újrasúlyozott, L 2 normás minimalizációk sorozatára vezeti vissza: IRWL 2 lim (W (l,t) t i,j = argmin W { 1 μ W W (l) 2 i,j 2 + ρ W Frobenius (l,t 1) W i,j Frobenius + ε }) (26)
25 4.2.3 Súlyok regularizálása csoportosan Fully connceted neurális háló esetén az l + 1-edik rétegében egy neuron aktivációját az alábbi összefüggés definiálja: (l+1) (l+1) L j = Wj,k Ahol L l az l-edik réteg neuronjainak vektora, W l a két réteg közötti súlymátrix. k Konvolúciós rétegek esetén az l + 1. réteg egy pixelének aktivációját definiálja a következő kifejezés: L k l L l+1 i (u, v) = ( W (l+1) i,j (u, v ) L i j (u u, v v ) ) j u,v (28) ahol L l l j a l. réteg j. csatornája, W i,j pedig egy NxN méretű konvolúciós szűrő ablak. Mindkét 2 hálótípus esetében elterjedten alkalmazzák Welemeire az L 1 és L 2 regularizációkat, melyek hatását korábban már ismertettem. Azonban CNN-ek esetén érdemes a 28) összefüggést a következő alakra hozni és úgy is megvizsgálni: (27) ahol az L l l az l. réteg csatornáit, a W i,j (l+1) (l+1) L i = Wi,j j L j i pedig a két csatorna közti konvolúciós kernel. (29) A konvolúciós hálók csatornái interpretálhatók a fully connected háló neuronjainak több dimenziós bemeneti jelet váró kiterjesztéseként. Mivel egy réteg csatornáit úgy kapjuk, hogy az előző réteg csatornáin lineáris szűrést végzünk és az eredményeket szuperponáljuk. 6. ábra A konvolúciós és fully connected rétegek analóg működése indokolja, hogy CCN-ek esetében súlyok helyett kernelenként regularizáljunk. Feltevésem szerint az általam korában definiált Tenzor L 0 regularizáció alkalmazása több szempontból is célravezetőbb, mint a szokásos L 1 és L 2 2. Előszöris így nem 0 súlyokat, hanem nullmátrix filterket kapunk, ami jelentősen redukálja a számítási erőforrásigényeket. Nullmátrix-szal való konvolúció eredménye ugyanis minden pixelében 0 kimenetet eredményez, tehát ezt ki sem kell számítani.
26 (l+1) Az ilyen módon kinullázott W i,j interpretációja az, hogy az l Lj csatorna nem vesz részt az (l+1) L i csatorna értékeinek definiálásában. Ez azért lehet hatékonyabb, mint a [10]-ben javasol módszer, mert az azzal analóg megoldás az lenne, ha bizonyos megfontolások mentén csatornákat dobnánk el. Ezzel a módszerrel viszont nem dobjuk el, csak egymást követő rétegbeli csatornapárok közötti függőség szűnik meg. Ez pedig olyan pozitív következményekkel járhat, hogy csatornák diverzifikálódni tudnak a későbbi rétegek, illetve maga a hálónak tanított feladat igényei szerint. Hasonló megfontolásból érdemes lehet a kilapítás utáni első réteg súlyait is csoportosítva regularizálni. Ugyanis a kilapítás lényegében csak egy implementációs trükk, arra, hogy átmenetet képezzen a jellemző kiemelést végző konvolúciós és a végső döntést hozó fully connected rétegek között. Igazából az utolsó réteg csatornáit látjuk sorosítva. Ezt az adathalmazt ugyanúgy értelmetlen pixelenként feldolgozni, sokkal hasznosabb lehet, ha a hiba-visszaterjesztés során azt a kérdést tesszük fel, hogy az adott csatorna fontos szerepet játszik-e adott neuron szempontjából. Érdemes azt is figyelembe venni, hogy a regularizációt sok esetben robosztusság növelése céljából alkalmazzuk. Viszont egy-egy szűrés szomszédos pixelei között a szűrések természetéből fakadóan jelentős korreláció adódik, ezért a pixelenkénti ritkító súlyregularizáció nem csökkentené a háló zavarérzékenységét, hanem épp ellenkezőleg, minden bizonnyal növelné. 7. ábra Az első fully connected réteg esetében szintén érdemesebb logikailag egybetartozónak tekinteni egy csatorna pixeleit és ez alapján csoportosan regularizálni a súlyokat Megvalósítás Kerasban lehetőség van callback függvények megadására. Ezek olyan függvények, amiket a felhasználó definiál és be tudja állítani, hogy a tanítás során mikor fussanak le. Tipikus példa a használatára a korai leállás implementálása, aminek a lényege, hogy ha előre definiált számú epoch óta nem javult a validáló mintákon a háló hibája, akkor leállítja a tanítást. Ezzel elkerülve a tanító adatokra történő túlilleszkedést és ezzel együtt a háló általánosító képességének a romlását. Ilyen callback függvény segítségével valósítottam meg a Tenzor L 0 regularizációt is. Ez azért tehető meg, mivel a proximity gradient minden iterációjának első lépése pontosan a gradient descent által is végzett súly frissítés, tehát ezt a keretrendszer el is végzi. Ha pedig
27 a callbackben implementáljuk a proximity gradient algoritmus második lépését, akkor pontosan az elvárt működést kapjuk. Mivel a callback-en belül minden szűrő súlymátrixát el lehet kérni, a konvolúciók esetében a következőképpen jártam el. Minden epoch végén minden tanult konvolúciós szűrőnek kiszámoltam a Frobenius-normáját és ha az egy, a tanítás elején megadott hipeparaméternél kisebb, akkor a mátrixot kinulláztam. A kilapítás utáni első réteg regularizációja esetén ehhez hasonlóan kell eljárni (csak arra az implementációs részletre kell ügyelni, hogy helyesen állítsuk vissza a sorosított mátrix dimenzióit) Tapasztalatok A vizsgált háló struktúrája a következő: 0. réteg: STN réteg (kimeneti kép: 30x30, bilineáris interpoláció) 1. réteg: 2D konvolúció (ablakméret: 3x3, kimeneti csatornák száma: 32, aktiváció: relu) 2. réteg: maxpooling, (ablakméret: 2x2) 3. réteg: 2D konvolúció (ablakméret: 3x3, kimeneti csatornák száma: C n, aktiváció: relu) 4. réteg: maxpooling, (ablakméret: 2x2) 5. réteg: flatten 6. réteg: fully connected (neuronok száma: 10, aktiváció: softmax) ahol a C n értéket 32-re állítva már korábban vizsgált hálót kapunk. Természetesen minimális eltéréseket tapasztalhatunk az újramérések során. Minden esetben egyszerre két rétegen próbáltam ki a Tenzor L 0 regularizációt: az utolsó konvolúciós rétegen és a kilapítás utáni első rétegen. Tapasztalataim alapján a regularizáció hatásosabb, ha ezekhez két eltérő hiperparamétert használunk, így a konvolúciós réteg küszöbértékét H c -vel a fullyconnected rétegét H f -fel jelölöm. A mérési eredmények az 6. táblázatban találhatóak. C n tanító 93,71% 94,49% 93,51% validáló 92,19% 92,59% 92,03% tesztelő 92,15% 92,37% 91,57% H c H f kinullázott kernelek 0 / / / 4096 kinullázott csatornák 0 / / / táblázat A Tenzor L 0 regularizáció hatása különböző paraméter értékek esetén. A mérések során a hieprparamétereket úgy hangoltam, hogy a megmaradó, nem csupa 0 szűrők / teljesen összekötött rétegbeli kapcsolatok súly paramétereinek a száma minél közelebb essen a regulrizálatlan 32 csatornás háló súlyainak a számához. Tapasztalati eredmények alapján a pontosságban nincs szignifikáns eltérés. Ezért kijelenthető, hogy
28 a jelenlegi, nem optimális implementáció mellett is képes volt a háló úgy redukálni a paramétereinek a számát, hogy hasonló eredményt ért el, mint a végig ugyanannyi paraméterrel tanított háló. Várhatóan ez az optimalizációs eljárás módosításával még javulna is. Továbbá azt is érdemes szem előtt tartani, hogy a páronként több független csatorna miatt az egyes szűrések specifikusabb transzformációkat tanulnak meg, mely alapján a háló döntésének értelmezése is javulhat. A három háló STN rétegének kimenetét a 8. ábrán láthatjuk. Ez alapján kvalitatíve a második kettő között nem mutatkozik különbség, de a 32 csatornás esetnél mindkettőn jobb pozícióba kerültek a számjegyek: mind az eltolásukat, mind az átskálázásukat tekintve jobb eredményt kaptunk. 8. ábra: A három háló STN rétegének kimenetei. A keretben 9 bemeneti kép látható. A többi az ezekhez a képekhez tartozó kimenetek a 32 (jobb felső), 64 (bal alsó) illetve 128 (jobb alsó) csatornás esetben. Ami még megállapítható, hogy a két konvolúciós réteg kimenetén valóban sokkal diverzebb képek jelennek meg a regularizált több csatornás hálók esetén. Ez igaz az első konvolúciós rétegre is, melynek szűrőit nem regularizáltuk. Ennek magyarázata, hogy ezek a csatornák is specializálódni tudtak a háló azon későbbi részeihez, melyek feldolgozták őket. A diverzifikációra a függelékben láthatunk mintát. Az ezt követő mérés során a Tenzor L 0 regularizáció hatékonyságát hasonlítottam össze egy a szakirodalmoban [9, 10] eddig javasolt módszerekhez hasonlóan működő eljárással. Ehhez az előző vizsgálat során használt hálón nem végeztem strukturális változtatást. Az összehasonlítás alapját képző paramter nyesési módszer esetén a betanított háló súlymátrixait törlöm Frobénus normájuk szerinti növekvő sorrendben. Ezzel a módszerrel pontosan megadható, hogy hány súlymátrixot akarunk elhagyni, így könnyen összehasonlítható a Tenzor L 0 regularizáció eredményével.
29 teszt pontosság 1 0,8 0,6 0,4 0, kinullázott súlyok száma regularizáció nyesés 9. ábra Az x tengelyen a Tensor L 0 segítségével kinullázott paraméterek száma (ez konvolúciós kernelenként 3 3, fully connected csoportosított súlyainál 6 6 súly egy mátrix kinullázásakor) az y tengelyen pedig az így kapott teszt pontosság a ClutteredMNIST adatbázison. A diagrammon jól látszik, hogy a nyeséshez képest körülbelül kétszeres mértékű paraméterredukció (30000 eldobott paraméter) esetén csökken a pontosság 80% alá. Az is leolvasható, hogy amikor a nyeséssel redukált háló már csak 10% körüli teljesítményre képes (vagyis véletlenszerű predikcióval azonos pontosságú) a Tenzor L 0 -val tanított háló még mindig 40% felett teljesít. Továbbá, hogy a töréspont a regularitázió teljesítményében csak kevéssel az után következik, miután kinullázható paraméterek több mint felét eliminálta. Részletesebb eredmények a függelékben találhatók Összefoglalás A javasolt regularizációs módszerrel tehát kvantitatíve jobbnak bizonyult a háló paraméterszám csökkentésében, mintha a szakirodalom által eddig tárgyalt tanítás utáni nyesét alkalmaznánk. Ezen felül bizonyos megfontolások mentén kvalitatíve is hatékonyabb megoldás születéséhez vezetett. Az így kapott hálóban a részfeladatok jobban különválaszthatók, így a predikciók magyarázata is könnyebbé válhat. Valószínűnek tartom, hogy más problémákra, illetve az IRWL2-es eljárással analóg optimalizáció alkalmazás esetén tovább javulna a regularizáció hatásossága.
30 Összefoglalás, továbbfejlesztési lehetőségek A dolgozat során olyan eljárásokat vizsgáltam meg és analizáltam, melyek alkalmazásával javítható a konvolúciós neurális hálók döntéseinek interpretálhatósága, illetve csökkenthető a háló komplexitása a pontosság tolerálható mértékű redukciója mellett. A tudás desztillálás széleskörűen elfogadott hálókompressziós módszer, melynek hatásosságát jelentősen sikerült meghaladni más megközelítések alkalmazásával. Ezek közül az első taglalt módszer a bemenetek uniformizálásához kapcsolódik, melyet automatizáltan az STN réteg alkalmazásával realizáltam. Mivel az STN réteg használatával logikailag is sikerül a háló által végzett műveletsort két részre bontani, így ezt a réteget nem kell interpretálni. Az STN által végzett uniformizálás hatására réteg kimenetére illesztett háló komplexitása nagyságrendileg csökken. Valamint a regisztráció következtében a megtanult szűrők között csökkenő redundancia miatt az interpretálhatóság is egyszerűsödik. A módszer hatásosságát kvalitatívan is megvizsgáltam, mely alapján a paraméterek számának 100-ad részre történő redukciója mellett a háló pontossága hozzávetőleg 5%-al csökkent a Cluttered MNIST adathalmazon. Sikerült olyan hálót is konstruálnom, mely csak egy konvolúciós és egy teljesen összekötött réteget tartalmazott az STN-en kívül, és az adathalmazon 90% feletti pontosságot ért el. A dolgozatban javaslatot tettem az STN-re épülő háló hatékonyságának további fokozására direkt regularizáció használatával. A szakirodalomban széleskörűen tárgyalt, ezért közismert elemenkénti regularizációs eljárások mellett a csoportonkénti regularizációs eljárások használatát is megvizsgáltam. Összehasonlítottam elvi megfontolások mentén a taglalt regularizációs módszereket, továbbá bevezettem egy ismereteim szerint más által eddig még nem vizsgált regularizációs büntetőfüggvényt, mely a Tensor L 0 normán alapult. Az implementált regularizációval nagy mértékben csökkentettem az STN alapú háló komplexitását. Ezen eljárás implementációs problémájával is foglalkoztam, mely analízis alapján a proximity gradient alapú numerikus optimalizációt választottam. Noha rámutattam hiányosságára, ezen optimalizáció alkalmazásával is jelentősen sikerült meghaladni a szakirodalomban publikált nyesési módszerek hatásosságát. A pontosság 3,21%-os esése mellett a szűrések 59%-ától sikerült megszabadultam. Lehetőségként javaslatot tettem az optimalizálási probléma újrasúlyozott Frobenius-normás regularizációra történő visszavezetésére (IRWL2-n alapuló optimalizáció), melyet a dolgozatban bemutatott kutatás folyományaként tervezek implementálni.
31 Irodalomjegyzék [1] Geoffrey Hinton, Oriol Vinyals, Jeff Dean Distilling the Knowledge in a Neural Network, arxiv , 2015 [2] Nicholas Frosst, Geoffrey Hinton Distilling a Neural Network Into a Soft Decision Tree, CEX 2017 [3] Ozan Irsoy, Olcay Taner Yıldız, Ethem Alpaydın, Soft Decision Trees, ICPR 2012 [4] Max Jaderberg, Karen Simonyan, Andrew Zisserman, Koray Kavukcuoglu Spatial Transformer Network, NIPS 2015, vol. 28, pp , [5] Alexey Kurakin, Ian Goodfellow, Samy Bengio Adversarial examples in the physical world, arxiv , 2016 [6] Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun Deep Residual Learning for Image Recognition, CVPR 2016, pp [7] Vincent Vanhoucke, Andrew Senior, Mark Z Mao, Improving the speed of neural networks on CPUs, NIPS 2011, [8] Suyog Gupta, Ankur Agrawal, Kailash Gopalakrishnan, Pritish Narayanan, Deep learning with limited numerical precision, ICML 2015, pp , 2015 [9] Yann Le Cun, John S. Denker, Sara A. Solla, Advances in neural information processing systems 2, D. S. Touretzky, Ed. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 1990, ch. Optimal Brain Damage, pp [10] Suraj Srinivas, R. Venkatesh Babu, Data-free Parameter Pruning for Deep Neural Networks, BMVC 2015, pp , 2015 [11] Emily Denton, Wojciech Zaremba, Joan Bruna, Yann LeCun, Rob Fergus, Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation, NIPS 2014, pp , 2014 [12] Peter Sollich, Anders Krogh, Ensemble Methods in Machine Learning: How overfitting can be useful, NIPS 1996, pp , The MIT Press, [13] Alex Krizhevsky, Ilya Sutskever, Geoffrey E. Hinton, ImageNet Classification with Deep Convolutional Neural Networks, NIPS 2012 [14] Sebastian Bach, Alexander Binder, Grégoire Montavon, Frederick Klauschen, Klaus-Robert Müller, Wojciech Samek, On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation, Doi /journal.pone , 2015 [15] Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, Zbigniew Wojna, Rethinking the Inception Architecture for Computer Vision, arxiv , 2015 [16] Forrest N. Iandola, Song Han, Matthew W. Moskewicz, Khalid Ashraf, William J. Dally, Kurt Keutzer, SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size, arxiv , 2016 [17] Alfredo Canziani, Adam Paszke, Eugenio Culurciello, An Analysis of Deep Neural Network Models for Practical Applications, arxiv , 2016
32 [18] Wenling Shang, Kihyuk Sohn, Diogo Almeida, Honglak Lee, Understanding and Improving Convolutional Neural Networks via Concatenated Rectified Linear Units, arxiv , 2016 [19] Max Pechyonkin, Understanding Hinton s Capsule Networks. Part I: Intuition. medium.com/ai³-theory-practice-business/understanding-hintons-capsule-networkspart-i-intuition-b4b559d1159b [20] Hui Zou, The Adaptive Lasso and Its Oracle Properties, Doi / [21] Emmanuel J. Candes, Michael B. Wakin, Stephen P. Boyd, Enhancing Sparsity by Reweighted L1 Minimization, arxiv , 2017 [22] Sara Sabour, Nicholas Frosst, Geoffrey E Hinton, Dynamic Routing Between Capsules, arxiv , 2017
33 Függelék A regularizáció és a nyesés közti különbséget ábrázoló diagram mérési pontjaihoz tartozó mérési eredmények részletesen: algoritmus: r=regularizáció, ny=nyesés tanító, validáló, tesztelő: százalékban értendő, az adott adathalmazon vett pontosság kernelek: a regularizált konvolúciós réteg kinullázott kerneleinek a száma az eredeti 2080* közül csatornák: a regularizált fully connected réteg súlymátrixai közül a kinullázottak száma (egy súlymátrix egy kilapítás előtti csatorna pixeleinek a súlyát tartalmazza) algoritmus r ny r ny r ny r ny r ny r ny r ny r ny tanító validáló tesztelő 94, , kernelek csatornák *az háló összes szűrőjének száma a kiinduláskor: 32+32*64 = 2080
34 Diverzifikáció: a b c d e f a: második konvolúciós réteg 32 csatorna, első konvolúciós réteg kimeneti csatornái b: második konvolúciós réteg 32 csatorna, második konvolúciós réteg kimeneti csatornái c: második konvolúciós réteg 64 csatorna, első konvolúciós réteg kimeneti csatornái d: második konvolúciós réteg 64 csatorna, második konvolúciós réteg kimeneti csatornái e: második konvolúciós réteg 128 csatorna, első konvolúciós réteg kimeneti csatornái f: második konvolúciós réteg 128 csatorna, második konvolúciós réteg kimeneti csatornái
Konvolúciós neurális hálózatok (CNN)
 Konvolúciós neurális hálózatok (CNN) Konvolúció Jelfeldolgozásban: Diszkrét jelek esetén diszkrét konvolúció: Képfeldolgozásban 2D konvolúció (szűrők): Konvolúciós neurális hálózat Konvolúciós réteg Kép,
Konvolúciós neurális hálózatok (CNN) Konvolúció Jelfeldolgozásban: Diszkrét jelek esetén diszkrét konvolúció: Képfeldolgozásban 2D konvolúció (szűrők): Konvolúciós neurális hálózat Konvolúciós réteg Kép,
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Intelligens Rendszerek Gyakorlata. Neurális hálózatok I.
 : Intelligens Rendszerek Gyakorlata Neurális hálózatok I. dr. Kutor László http://mobil.nik.bmf.hu/tantargyak/ir2.html IRG 3/1 Trend osztályozás Pnndemo.exe IRG 3/2 Hangulat azonosítás Happy.exe IRG 3/3
: Intelligens Rendszerek Gyakorlata Neurális hálózatok I. dr. Kutor László http://mobil.nik.bmf.hu/tantargyak/ir2.html IRG 3/1 Trend osztályozás Pnndemo.exe IRG 3/2 Hangulat azonosítás Happy.exe IRG 3/3
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
KONVOLÚCIÓS NEURONHÁLÓK. A tananyag az EFOP pályázat támogatásával készült.
 KONVOLÚCIÓS NEURONHÁLÓK A tananyag az EFOP-3.5.1-16-2017-00004 pályázat támogatásával készült. 1. motiváció A klasszikus neuronháló struktúra a fully connected háló Két réteg között minden neuron kapcsolódik
KONVOLÚCIÓS NEURONHÁLÓK A tananyag az EFOP-3.5.1-16-2017-00004 pályázat támogatásával készült. 1. motiváció A klasszikus neuronháló struktúra a fully connected háló Két réteg között minden neuron kapcsolódik
Intelligens Rendszerek Elmélete. Versengéses és önszervező tanulás neurális hálózatokban
 Intelligens Rendszerek Elmélete : dr. Kutor László Versengéses és önszervező tanulás neurális hálózatokban http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 9/1 Processzor Versengéses
Intelligens Rendszerek Elmélete : dr. Kutor László Versengéses és önszervező tanulás neurális hálózatokban http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 9/1 Processzor Versengéses
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
A maximum likelihood becslésről
 A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017.
 Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Intelligens orvosi műszerek VIMIA023
 Intelligens orvosi műszerek VIMIA023 Neurális hálók (Dobrowiecki Tadeusz anyagának átdolgozásával) 2017 ősz http://www.mit.bme.hu/oktatas/targyak/vimia023 dr. Pataki Béla pataki@mit.bme.hu (463-)2679 A
Intelligens orvosi műszerek VIMIA023 Neurális hálók (Dobrowiecki Tadeusz anyagának átdolgozásával) 2017 ősz http://www.mit.bme.hu/oktatas/targyak/vimia023 dr. Pataki Béla pataki@mit.bme.hu (463-)2679 A
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Gépi tanulás a gyakorlatban. Bevezetés
 Gépi tanulás a gyakorlatban Bevezetés Motiváció Nagyon gyakran találkozunk gépi tanuló alkalmazásokkal Spam detekció Karakter felismerés Fotó címkézés Szociális háló elemzés Piaci szegmentáció analízis
Gépi tanulás a gyakorlatban Bevezetés Motiváció Nagyon gyakran találkozunk gépi tanuló alkalmazásokkal Spam detekció Karakter felismerés Fotó címkézés Szociális háló elemzés Piaci szegmentáció analízis
Mély konvolúciós neurális hálózatok. Hadházi Dániel BME IE 338
 Mély konvolúciós neurális hálózatok Hadházi Dániel BME IE 338 hadhazi@mit.bme.hu ÚJ ARCHITEKTÚRÁLIS ELEMEK Konvolúciós réteg Motiváció: Klasszikus képfeldolgozásnál alapművelet a konvolúció: Zajszűrésre
Mély konvolúciós neurális hálózatok Hadházi Dániel BME IE 338 hadhazi@mit.bme.hu ÚJ ARCHITEKTÚRÁLIS ELEMEK Konvolúciós réteg Motiváció: Klasszikus képfeldolgozásnál alapművelet a konvolúció: Zajszűrésre
Konjugált gradiens módszer
 Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Mesterséges neurális hálózatok II. - A felügyelt tanítás paraméterei, gyorsító megoldásai - Versengéses tanulás
 Mesterséges neurális hálózatok II. - A felügyelt tanítás paraméterei, gyorsító megoldásai - Versengéses tanulás http:/uni-obuda.hu/users/kutor/ IRE 7/50/1 A neurális hálózatok általános jellemzői 1. A
Mesterséges neurális hálózatok II. - A felügyelt tanítás paraméterei, gyorsító megoldásai - Versengéses tanulás http:/uni-obuda.hu/users/kutor/ IRE 7/50/1 A neurális hálózatok általános jellemzői 1. A
Mérési struktúrák
 Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE
 I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
Osztályozási feladatok képdiagnosztikában. Orvosi képdiagnosztikai 2017 ősz
 Osztályozási feladatok képdiagnosztikában Orvosi képdiagnosztikai 2017 ősz Osztályozás Szeparáló felületet keresünk Leképezéseket tanulunk meg azok mintáiból A tanuláshoz használt minták a tanító minták
Osztályozási feladatok képdiagnosztikában Orvosi képdiagnosztikai 2017 ősz Osztályozás Szeparáló felületet keresünk Leképezéseket tanulunk meg azok mintáiból A tanuláshoz használt minták a tanító minták
Hipotézis STATISZTIKA. Kétmintás hipotézisek. Munkahipotézis (H a ) Tematika. Tudományos hipotézis. 1. Előadás. Hipotézisvizsgálatok
 STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
Konvexitás, elaszticitás
 DIFFERENCIÁLSZÁMÍTÁS ALKALMAZÁSAI Konveitás, elaszticitás Tanulási cél A másodrendű deriváltat vizsgálva milyen következtetéseket vonhatunk le a üggvény konveitására vonatkozóan. Elaszticitás ogalmának
DIFFERENCIÁLSZÁMÍTÁS ALKALMAZÁSAI Konveitás, elaszticitás Tanulási cél A másodrendű deriváltat vizsgálva milyen következtetéseket vonhatunk le a üggvény konveitására vonatkozóan. Elaszticitás ogalmának
[1000 ; 0] 7 [1000 ; 3000]
![[1000 ; 0] 7 [1000 ; 3000] [1000 ; 0] 7 [1000 ; 3000]](/thumbs/88/116286101.jpg) Gépi tanulás (vimim36) Gyakorló feladatok 04 tavaszi félév Ahol lehet, ott konkrét számértékeket várok nem puszta egyenleteket. (Azok egy részét amúgyis megadom.). Egy bináris osztályozási feladatra tanított
Gépi tanulás (vimim36) Gyakorló feladatok 04 tavaszi félév Ahol lehet, ott konkrét számértékeket várok nem puszta egyenleteket. (Azok egy részét amúgyis megadom.). Egy bináris osztályozási feladatra tanított
Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs rendszerek Tanszék. Neurális hálók. Pataki Béla
 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs rendszerek Tanszék Neurális hálók Előadó: Előadás anyaga: Hullám Gábor Pataki Béla Dobrowiecki Tadeusz BME I.E. 414, 463-26-79
Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs rendszerek Tanszék Neurális hálók Előadó: Előadás anyaga: Hullám Gábor Pataki Béla Dobrowiecki Tadeusz BME I.E. 414, 463-26-79
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
GPU Lab. 14. fejezet. OpenCL textúra használat. Grafikus Processzorok Tudományos Célú Programozása. Berényi Dániel Nagy-Egri Máté Ferenc
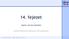 14. fejezet OpenCL textúra használat Grafikus Processzorok Tudományos Célú Programozása Textúrák A textúrák 1, 2, vagy 3D-s tömbök kifejezetten szín információk tárolására Főbb különbségek a bufferekhez
14. fejezet OpenCL textúra használat Grafikus Processzorok Tudományos Célú Programozása Textúrák A textúrák 1, 2, vagy 3D-s tömbök kifejezetten szín információk tárolására Főbb különbségek a bufferekhez
Gépi tanulás a gyakorlatban. Kiértékelés és Klaszterezés
 Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
y ij = µ + α i + e ij
 Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
6. gyakorlat. Gelle Kitti. Csendes Tibor Somogyi Viktor. London András. jegyzetei alapján
 Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz
 Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz Szekér Szabolcs 1, Dr. Fogarassyné dr. Vathy Ágnes 2 1 Pannon Egyetem Rendszer- és Számítástudományi Tanszék, szekersz@gmail.com
Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz Szekér Szabolcs 1, Dr. Fogarassyné dr. Vathy Ágnes 2 1 Pannon Egyetem Rendszer- és Számítástudományi Tanszék, szekersz@gmail.com
Optimalizálás alapfeladata Legmeredekebb lejtő Lagrange függvény Log-barrier módszer Büntetőfüggvény módszer 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Neurális hálózatok bemutató
 Neurális hálózatok bemutató Füvesi Viktor Miskolci Egyetem Alkalmazott Földtudományi Kutatóintézet Miért? Vannak feladatok amelyeket az agy gyorsabban hajt végre mint a konvencionális számítógépek. Pl.:
Neurális hálózatok bemutató Füvesi Viktor Miskolci Egyetem Alkalmazott Földtudományi Kutatóintézet Miért? Vannak feladatok amelyeket az agy gyorsabban hajt végre mint a konvencionális számítógépek. Pl.:
Legkisebb négyzetek módszere, Spline interpoláció
 Közelítő és szimbolikus számítások 10. gyakorlat Legkisebb négyzetek módszere, Spline interpoláció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján
Közelítő és szimbolikus számítások 10. gyakorlat Legkisebb négyzetek módszere, Spline interpoláció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján
I. LABOR -Mesterséges neuron
 I. LABOR -Mesterséges neuron A GYAKORLAT CÉLJA: A mesterséges neuron struktúrájának az ismertetése, neuronhálókkal kapcsolatos elemek, alapfogalmak bemutatása, aktivációs függvénytípusok szemléltetése,
I. LABOR -Mesterséges neuron A GYAKORLAT CÉLJA: A mesterséges neuron struktúrájának az ismertetése, neuronhálókkal kapcsolatos elemek, alapfogalmak bemutatása, aktivációs függvénytípusok szemléltetése,
Lineáris regressziós modellek 1
 Lineáris regressziós modellek 1 Ispány Márton és Jeszenszky Péter 2016. szeptember 19. 1 Az ábrák C.M. Bishop: Pattern Recognition and Machine Learning c. könyvéből származnak. Tartalom Bevezető példák
Lineáris regressziós modellek 1 Ispány Márton és Jeszenszky Péter 2016. szeptember 19. 1 Az ábrák C.M. Bishop: Pattern Recognition and Machine Learning c. könyvéből származnak. Tartalom Bevezető példák
10. Előadás. 1. Feltétel nélküli optimalizálás: Az eljárás alapjai
 Optimalizálási eljárások MSc hallgatók számára 10. Előadás Előadó: Hajnal Péter Jegyzetelő: T. Szabó Tamás 2011. április 20. 1. Feltétel nélküli optimalizálás: Az eljárás alapjai A feltétel nélküli optimalizálásnál
Optimalizálási eljárások MSc hallgatók számára 10. Előadás Előadó: Hajnal Péter Jegyzetelő: T. Szabó Tamás 2011. április 20. 1. Feltétel nélküli optimalizálás: Az eljárás alapjai A feltétel nélküli optimalizálásnál
A KLT (Kanade Lucas Tomasi) Feature Tracker Működése (jellegzetes pontok választása és követése)
 A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Google Summer of Code Project
 Neuronhálózatok a részecskefizikában Bagoly Attila ELTE TTK Fizikus MSc, 2. évfolyam Integrating Machine Learning in Jupyter Notebooks Google Summer of Code Project 2016.10.10 Bagoly Attila (ELTE) Machine
Neuronhálózatok a részecskefizikában Bagoly Attila ELTE TTK Fizikus MSc, 2. évfolyam Integrating Machine Learning in Jupyter Notebooks Google Summer of Code Project 2016.10.10 Bagoly Attila (ELTE) Machine
Intelligens Rendszerek Elmélete
 Intelligens Rendszerek Elmélete Dr. Kutor László : Mesterséges neurális hálózatok felügyelt tanítása hiba visszateresztő Back error Propagation algoritmussal Versengéses tanulás http://mobil.nik.bmf.hu/tantargyak/ire.html
Intelligens Rendszerek Elmélete Dr. Kutor László : Mesterséges neurális hálózatok felügyelt tanítása hiba visszateresztő Back error Propagation algoritmussal Versengéses tanulás http://mobil.nik.bmf.hu/tantargyak/ire.html
Rendszámfelismerő rendszerek
 Problémamegoldó szeminárium Témavezető: Pataki Péter ARH Zrt. ELTE-TTK 2013 Tartalomjegyzék 1 Bevezetés 2 Út a megoldás felé 3 Felmerült problémák 4 Alkalmazott matematika 5 További lehetőségek Motiváció
Problémamegoldó szeminárium Témavezető: Pataki Péter ARH Zrt. ELTE-TTK 2013 Tartalomjegyzék 1 Bevezetés 2 Út a megoldás felé 3 Felmerült problémák 4 Alkalmazott matematika 5 További lehetőségek Motiváció
Saj at ert ek-probl em ak febru ar 26.
 Sajátérték-problémák 2018. február 26. Az alapfeladat Adott a következő egyenlet: Av = λv, (1) ahol A egy ismert mátrix v ismeretlen, nem zérus vektor λ ismeretlen szám Azok a v, λ kombinációk, amikre
Sajátérték-problémák 2018. február 26. Az alapfeladat Adott a következő egyenlet: Av = λv, (1) ahol A egy ismert mátrix v ismeretlen, nem zérus vektor λ ismeretlen szám Azok a v, λ kombinációk, amikre
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével. MAJF21 Eisenberger András május 22. Konzulens: Dr.
 Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével 2011. május 22. Konzulens: Dr. Pataki Béla Tartalomjegyzék 1. Bevezetés 2 2. Források 2 3. Kiértékelő szoftver 3 4. A képek feldolgozása
Önálló labor beszámoló Képek szegmentálása textúra analízis segítségével 2011. május 22. Konzulens: Dr. Pataki Béla Tartalomjegyzék 1. Bevezetés 2 2. Források 2 3. Kiértékelő szoftver 3 4. A képek feldolgozása
Panorámakép készítése
 Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Biomatematika 13. Varianciaanaĺızis (ANOVA)
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 13. Varianciaanaĺızis (ANOVA) Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision Date:
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 13. Varianciaanaĺızis (ANOVA) Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision Date:
Méréselmélet MI BSc 1
 Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Struktúra nélküli adatszerkezetek
 Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Képfeldolgozás Szegmentálás Osztályozás Képfelismerés Térbeli rekonstrukció
 Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Gauss-Jordan módszer Legkisebb négyzetek módszere, egyenes LNM, polinom LNM, függvény. Lineáris algebra numerikus módszerei
 A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
Hadamard-mátrixok Előadó: Hajnal Péter február 23.
 Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Geofizikai kutatómódszerek I.
 Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
y ij = µ + α i + e ij STATISZTIKA Sir Ronald Aylmer Fisher Példa Elmélet A variancia-analízis alkalmazásának feltételei Lineáris modell
 Példa STATISZTIKA Egy gazdálkodó k kukorica hibrid termesztése között választhat. Jelöljük a fajtákat A, B, C, D-vel. Döntsük el, hogy a hibridek termesztése esetén azonos terméseredményre számíthatunk-e.
Példa STATISZTIKA Egy gazdálkodó k kukorica hibrid termesztése között választhat. Jelöljük a fajtákat A, B, C, D-vel. Döntsük el, hogy a hibridek termesztése esetén azonos terméseredményre számíthatunk-e.
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén
 Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
A mérések általános és alapvető metrológiai fogalmai és definíciói. Mérések, mérési eredmények, mérési bizonytalanság. mérés. mérési elv
 Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
A szimplex algoritmus
 A szimplex algoritmus Ismétlés: reprezentációs tétel, az optimális megoldás és az extrém pontok kapcsolata Alapfogalmak: bázisok, bázismegoldások, megengedett bázismegoldások, degenerált bázismegoldás
A szimplex algoritmus Ismétlés: reprezentációs tétel, az optimális megoldás és az extrém pontok kapcsolata Alapfogalmak: bázisok, bázismegoldások, megengedett bázismegoldások, degenerált bázismegoldás
Deep Learning a gyakorlatban Python és LUA alapon Tanítás: alap tippek és trükkök
 Gyires-Tóth Bálint Deep Learning a gyakorlatban Python és LUA alapon Tanítás: alap tippek és trükkök http://smartlab.tmit.bme.hu Deep Learning Híradó Hírek az elmúlt 168 órából Deep Learning Híradó Google
Gyires-Tóth Bálint Deep Learning a gyakorlatban Python és LUA alapon Tanítás: alap tippek és trükkök http://smartlab.tmit.bme.hu Deep Learning Híradó Hírek az elmúlt 168 órából Deep Learning Híradó Google
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
CARE. Biztonságos. otthonok idős embereknek CARE. Biztonságos otthonok idős embereknek 2010-09-02. Dr. Vajda Ferenc Egyetemi docens
 CARE Biztonságos CARE Biztonságos otthonok idős embereknek otthonok idős embereknek 2010-09-02 Dr. Vajda Ferenc Egyetemi docens 3D Érzékelés és Mobilrobotika kutatócsoport Budapesti Műszaki és Gazdaságtudományi
CARE Biztonságos CARE Biztonságos otthonok idős embereknek otthonok idős embereknek 2010-09-02 Dr. Vajda Ferenc Egyetemi docens 3D Érzékelés és Mobilrobotika kutatócsoport Budapesti Műszaki és Gazdaságtudományi
1. gyakorlat. Mesterséges Intelligencia 2.
 1. gyakorlat Mesterséges Intelligencia. Elérhetőségek web: www.inf.u-szeged.hu/~gulyasg mail: gulyasg@inf.u-szeged.hu Követelmények (nem teljes) gyakorlat látogatása kötelező ZH írása a gyakorlaton elhangzott
1. gyakorlat Mesterséges Intelligencia. Elérhetőségek web: www.inf.u-szeged.hu/~gulyasg mail: gulyasg@inf.u-szeged.hu Követelmények (nem teljes) gyakorlat látogatása kötelező ZH írása a gyakorlaton elhangzott
Gépi tanulás a gyakorlatban. Lineáris regresszió
 Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
A mérés problémája a pedagógiában. Dr. Nyéki Lajos 2015
 A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
Tanulás az idegrendszerben. Structure Dynamics Implementation Algorithm Computation - Function
 Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
Tanulás az idegrendszerben Structure Dynamics Implementation Algorithm Computation - Function Tanulás pszichológiai szinten Classical conditioning Hebb ötlete: "Ha az A sejt axonja elég közel van a B sejthez,
RE 1. Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
RE 1 Relációk Függvények RE 2 Definíció: Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor azt mondjuk, hogy
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 8. Előadás Dr. Kulcsár Gyula egyetemi docens Kereső algoritmusok alkalmazása
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 8. Előadás Dr. Kulcsár Gyula egyetemi docens Kereső algoritmusok alkalmazása
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
Matematikai modellezés
 Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
Hipotézis vizsgálatok
 Hipotézis vizsgálatok Hipotézisvizsgálat Hipotézis: az alapsokaság paramétereire vagy az alapsokaság eloszlására vonatkozó feltevés. Hipotézis ellenőrzés: az a statisztikai módszer, amelynek segítségével
Hipotézis vizsgálatok Hipotézisvizsgálat Hipotézis: az alapsokaság paramétereire vagy az alapsokaság eloszlására vonatkozó feltevés. Hipotézis ellenőrzés: az a statisztikai módszer, amelynek segítségével
Visszacsatolt (mély) neurális hálózatok
 Visszacsatolt (mély) neurális hálózatok Visszacsatolt hálózatok kimenet rejtett rétegek bemenet Sima előrecsatolt neurális hálózat Visszacsatolt hálózatok kimenet rejtett rétegek bemenet Pl.: kép feliratozás,
Visszacsatolt (mély) neurális hálózatok Visszacsatolt hálózatok kimenet rejtett rétegek bemenet Sima előrecsatolt neurális hálózat Visszacsatolt hálózatok kimenet rejtett rétegek bemenet Pl.: kép feliratozás,
PIXEL SZINTŰ SZEGMENTÁLÁS CNN-EL
 PIXEL SZINTŰ SZEGMENTÁLÁS CNN-EL Csúszóablakos szegmentálás Szegmentálás direkt osztályozással Kisméretű ablakkal kivágott kép alapján megítéli az adott pixel környezetének a típusát Nagyon lassú, nehezen
PIXEL SZINTŰ SZEGMENTÁLÁS CNN-EL Csúszóablakos szegmentálás Szegmentálás direkt osztályozással Kisméretű ablakkal kivágott kép alapján megítéli az adott pixel környezetének a típusát Nagyon lassú, nehezen
Hipotézis, sejtés STATISZTIKA. Kétmintás hipotézisek. Tudományos hipotézis. Munkahipotézis (H a ) Nullhipotézis (H 0 ) 11. Előadás
 STATISZTIKA Hipotézis, sejtés 11. Előadás Hipotézisvizsgálatok, nem paraméteres próbák Tudományos hipotézis Nullhipotézis felállítása (H 0 ): Kétmintás hipotézisek Munkahipotézis (H a ) Nullhipotézis (H
STATISZTIKA Hipotézis, sejtés 11. Előadás Hipotézisvizsgálatok, nem paraméteres próbák Tudományos hipotézis Nullhipotézis felállítása (H 0 ): Kétmintás hipotézisek Munkahipotézis (H a ) Nullhipotézis (H
Dinamikus modellek szerkezete, SDG modellek
 Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján. Típusok: felügyelt és felügyelet nélküli tanuló eljárások
 Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján Típusok: felügyelt és felügyelet nélküli tanuló eljárások Különbség: előbbinél szükséges egy olyan tanulóhalmaz, ahol ismert a minták
Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján Típusok: felügyelt és felügyelet nélküli tanuló eljárások Különbség: előbbinél szükséges egy olyan tanulóhalmaz, ahol ismert a minták
Relációk Függvények. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 függvények RE 1 Relációk Függvények függvények RE 2 Definíció Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor
függvények RE 1 Relációk Függvények függvények RE 2 Definíció Ha A, B és ρ A B, akkor azt mondjuk, hogy ρ reláció A és B között, vagy azt, hogy ρ leképezés A-ból B-be. Ha speciálisan A=B, azaz ρ A A, akkor
3. Szűrés képtérben. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Biostatisztika VIII. Mátyus László. 19 October
 Biostatisztika VIII Mátyus László 19 October 2010 1 Ha σ nem ismert A gyakorlatban ritkán ismerjük σ-t. Ha kiszámítjuk s-t a minta alapján, akkor becsülhetjük σ-t. Ez további bizonytalanságot okoz a becslésben.
Biostatisztika VIII Mátyus László 19 October 2010 1 Ha σ nem ismert A gyakorlatban ritkán ismerjük σ-t. Ha kiszámítjuk s-t a minta alapján, akkor becsülhetjük σ-t. Ez további bizonytalanságot okoz a becslésben.
Gépi tanulás. Hány tanítómintára van szükség? VKH. Pataki Béla (Bolgár Bence)
 Gépi tanulás Hány tanítómintára van szükség? VKH Pataki Béla (Bolgár Bence) BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Induktív tanulás A tanítás folyamata: Kiinduló
Gépi tanulás Hány tanítómintára van szükség? VKH Pataki Béla (Bolgár Bence) BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Induktív tanulás A tanítás folyamata: Kiinduló
E x μ x μ K I. és 1. osztály. pontokként), valamint a bayesi döntést megvalósító szeparáló görbét (kék egyenes)
 6-7 ősz. gyakorlat Feladatok.) Adjon meg azt a perceptronon implementált Bayes-i klasszifikátort, amely kétdimenziós a bemeneti tér felett szeparálja a Gauss eloszlású mintákat! Rajzolja le a bemeneti
6-7 ősz. gyakorlat Feladatok.) Adjon meg azt a perceptronon implementált Bayes-i klasszifikátort, amely kétdimenziós a bemeneti tér felett szeparálja a Gauss eloszlású mintákat! Rajzolja le a bemeneti
ACM Snake. Orvosi képdiagnosztika 11. előadás első fele
 ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
STATISZTIKA. A maradék független a kezelés és blokk hatástól. Maradékok leíró statisztikája. 4. A modell érvényességének ellenőrzése
 4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
Sergyán Szabolcs szeptember 21.
 Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Irányításelmélet és technika II.
 Irányításelmélet és technika II. Legkisebb négyzetek módszere Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék amagyar@almos.vein.hu 200 november
Irányításelmélet és technika II. Legkisebb négyzetek módszere Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék amagyar@almos.vein.hu 200 november
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
KUTATÁSI JELENTÉS. Multilaterációs radarrendszer kutatása. Szüllő Ádám
 KUTATÁSI JELENTÉS Multilaterációs radarrendszer kutatása Szüllő Ádám 212 Bevezetés A Mikrohullámú Távérzékelés Laboratórium jelenlegi K+F tevékenységei közül ezen jelentés a multilaterációs radarrendszerek
KUTATÁSI JELENTÉS Multilaterációs radarrendszer kutatása Szüllő Ádám 212 Bevezetés A Mikrohullámú Távérzékelés Laboratórium jelenlegi K+F tevékenységei közül ezen jelentés a multilaterációs radarrendszerek
Tanulás tanuló gépek tanuló algoritmusok mesterséges neurális hálózatok
 Zrínyi Miklós Gimnázium Művészet és tudomány napja Tanulás tanuló gépek tanuló algoritmusok mesterséges neurális hálózatok 10/9/2009 Dr. Viharos Zsolt János Elsősorban volt Zrínyis diák Tudományos főmunkatárs
Zrínyi Miklós Gimnázium Művészet és tudomány napja Tanulás tanuló gépek tanuló algoritmusok mesterséges neurális hálózatok 10/9/2009 Dr. Viharos Zsolt János Elsősorban volt Zrínyis diák Tudományos főmunkatárs
Digitális mérőműszerek. Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt.
 Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt. MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális jel esetében?
Digitális mérőműszerek Digitális jelek mérése Kaltenecker Zsolt Hiradástechnikai Villamosmérnök Szinusz Hullám Bt. MIRŐL LESZ SZÓ? Mit mérjünk? Hogyan jelentkezik a minőségromlás digitális jel esetében?
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Nagyságrendek. Kiegészítő anyag az Algoritmuselmélet tárgyhoz. Friedl Katalin BME SZIT február 1.
 Nagyságrendek Kiegészítő anyag az Algoritmuselmélet tárgyhoz (a Rónyai Ivanyos Szabó: Algoritmusok könyv mellé) Friedl Katalin BME SZIT friedl@cs.bme.hu 018. február 1. Az O, Ω, Θ jelölések Az algoritmusok
Nagyságrendek Kiegészítő anyag az Algoritmuselmélet tárgyhoz (a Rónyai Ivanyos Szabó: Algoritmusok könyv mellé) Friedl Katalin BME SZIT friedl@cs.bme.hu 018. február 1. Az O, Ω, Θ jelölések Az algoritmusok
társadalomtudományokban
 Gépi tanulás, predikció és okság a társadalomtudományokban Muraközy Balázs (MTA KRTK) Bemutatkozik a Számítógépes Társadalomtudomány témacsoport, MTA, 2017 2/20 Empirikus közgazdasági kérdések Felváltja-e
Gépi tanulás, predikció és okság a társadalomtudományokban Muraközy Balázs (MTA KRTK) Bemutatkozik a Számítógépes Társadalomtudomány témacsoport, MTA, 2017 2/20 Empirikus közgazdasági kérdések Felváltja-e
Modellezés és szimuláció. Szatmári József SZTE Természeti Földrajzi és Geoinformatikai Tanszék
 Modellezés és szimuláció Szatmári József SZTE Természeti Földrajzi és Geoinformatikai Tanszék Kvantitatív forradalmak a földtudományban - geográfiában 1960- as évek eleje: statisztika 1970- as évek eleje:
Modellezés és szimuláció Szatmári József SZTE Természeti Földrajzi és Geoinformatikai Tanszék Kvantitatív forradalmak a földtudományban - geográfiában 1960- as évek eleje: statisztika 1970- as évek eleje:
Statisztikai módszerek 7. gyakorlat
 Statisztikai módszerek 7. gyakorlat A tanult nem paraméteres próbák: PRÓBA NEVE Illeszkedés-vizsgálat Χ 2 próbával Homogenitás-vizsgálat Χ 2 próbával Normalitás-vizsgálataΧ 2 próbával MIRE SZOLGÁL? A val.-i
Statisztikai módszerek 7. gyakorlat A tanult nem paraméteres próbák: PRÓBA NEVE Illeszkedés-vizsgálat Χ 2 próbával Homogenitás-vizsgálat Χ 2 próbával Normalitás-vizsgálataΧ 2 próbával MIRE SZOLGÁL? A val.-i
