Latin négyzetek alkalmazásai a tervezésben és kódolásban
|
|
|
- Ödön Illés
- 8 évvel ezelőtt
- Látták:
Átírás
1 Latin négyzetek alkalmazásai a tervezésben és kódolásban DÉNES TAMÁS tdenest@fre .hu Kulcsszavak: vizsgálat-optimalizálás, titkosítás, adatbiztonság, képkódolás A latin négyzeteket a gyakorlatban fôleg három területen alkalmazzák. Ezek a következôk: a statisztikus kísérlet-tervezés, a kódolás (hírközlési alkalmazásként) és a titkosítás. Míg a statisztikai alkalmazásokban R. A. Fisher tekinthetô úttörônek, az 1920-as években megkezdett tevékenységével és híres könyvével (The design of experiments), addig a latin négyzetek alkalmazása a hírközlésben a II. világháborút megelôzôen kezdôdött mind amerikai, mind német részrôl. Az elsô publikált eredmények azonban, érthetô okokból, csak a háború befejezése után jelentek meg. Amerikai részrôl C. E. Shannon, német részrôl pedig Rudolf Schauffler nevét kell megemlíteni úttörôként, aki a német rejtjelfejtés kimagasló alakja volt a II. világháború alatt. Az 1/a. ábrán látható latin négyzet úgy alkalmazható a kísérletek tervezésénél, hogy az oszlop kiválasztással a kezelôt, a sor kiválasztással a szövôgépet és a kiválasztott sor és oszlop metszetében álló elemmel az adott kísérletben felhasznált fonalat határozzuk meg. Így például az elsô kísérlet: a K 1 gépkezelô az S 1 szövôgépen Y 1 fonallal dolgozik. 1. Alkalmazások a statisztikus kísérlet tervezésben R. A. Fisher szerint szemben az addigi gyakorlattal, amikor is a kísérletek során csak egyetlen tényezôt változtattak célszerû az összes tényezô egyidejû variálása. Így jött létre a statisztika egy új ága, a faktor-analízis, valamint a latin négyzetek kísérletek tervezésében való felhasználása. Az ortogonális latin négyzetek statisztikai alkalmazását egy példán keresztül szemléltetem. Öt különféle kikészítésû szálból szôtt késztermék mintázatát kell minôségileg összehasonlítani. A késztermék elôállításán öt szövôgépen öt gépkezelô dolgozik. Az a feltételezés (amit igazolni kell), hogy a szálak kikészítésén kívül a szövéshez felhasznált gép és kezelôje is minôséget befolyásoló tényezôk. Ha a kísérletekre szánt idô nem lenne korlátozó tényezô, akkor minden egyes fonalfajtát mind az öt szövôgépen az öt gépkezelô mindegyikével ki kellene próbálni. Ez összesen 125 kísérletet jelent. A latin négyzetek segítségével azonban kielégítô eredményt lehet elérni egy 25 kísérletbôl álló kísérletsorozattal. Tegyük fel, hogy K 1, K 2,, K 5 jelöli az öt gépkezelôt, S 1, S 2,, S 5 jelöli az öt szövôgépet, valamint Y 1, Y 2,, Y 5 az öt különféle szál jelölésére szolgál. A minôség összevetésére szolgáló 25 kísérletet az 1. ábrán bemutatott latin négyzet szemlélteti. 1/a. ábra 1/b. ábra Tegyük fel továbbá, hogy a gépkezelôk hatékonyságát befolyásolja, hogy a hét mely munkanapján dolgoznak. Akkor az 1/a. ábrán megadott latin négyzetben szereplô indexekhez (lásd 1/b. ábra) tartozó ortogonális párt kell szerkeszteni (lásd 2/a. ábra), ahol a munkanapokat számok jelzik. (1=hétfô, 2=kedd, 3= szerda, 4=csütörtök, 5=péntek.) 2/a. ábra 2/b. ábra A két ortogonális latin négyzet (lásd az 1/b. és 2/a. ábrán) egymásra helyezésével megszerkesztett 25 kísérletbôl álló kísérletsorozatot ábrázolja a 2/b. ábra, amely lehetôvé teszi, hogy minden egyes gépkezelô minden egyes szövôgépen dolgozzon, a munkájában az öt különbözô kikészítésû fonal mindegyikét pontosan egyszer használja és a vele kapcsolatos kísérleteknél egy hét 5 munkanapja közül minden napra egy kísérlet jusson. 40 LIX. ÉVFOLYAM 2005/1
2 Latin négyzetek alkalmazásai... Hasonló típusú kísérletek megtervezése merül fel például a növénytermesztés, vagy a gyógyszerkutatás területén is. Nyilvánvaló, hogy a kísérlet tervezésénél a latin négyzetek alkalmazhatósága bizonyos szempontból korlátozott, hiszen ha az elôbbi példánkban például a gépkezelôk száma nem öt, hanem négy, akkor már másfajta elrendezésre van szükség. Az ilyen, a latin négyzeteknél általánosabb elrendezéseket block designoknak nevezzük. Az érdeklôdô olvasó jó betekintést kaphat a block designokról [6]-bôl. Egy másik példa világítja meg a teljes latin négyzetek alkalmazását a kísérletek tervezésében. Egy állatkísérletben a kísérleti állatokat különbözô étrend szerint táplálják, feltevés szerint (amit a kísérletek során ellenôrizni kívánnak) egy adott állat etetése elôtt, a kísérlet során kapott összes étkezések száma, valamint a közvetlenül megelôzô etetés során kapott takarmány fajtája befolyásolja az eredményt. Tegyük fel, hogy n darab állat és n féle takarmány kerül a kísérletben felhasználásra. n=4 esetén az A 1, A 2, A 3, A 4 kísérleti állatot a T 1, T 2, T 3, T 4 takarmányokkal táplálják a 3. ábrán látható teljes latin négyzet szerinti kísérleti elrendezésben. A latin négyzeteken alapuló nem bináris hibajelzô és javító kódok elterjedéséhez a feltételt azonban a szélessávú ûrtávközlési csatornák megjelenése teremtette meg. Ezért S. W. Golomb és E. C. Posner a JPL (Jet Propulation Laboratory) pasadénai kutatólaboratórium vezetô munkatársaiként foglalkoztak a hibajelzô és javító kódok latin négyzetek alapján való szerkesztésével. Eredményüket a következôkben lehet megfogalmazni: Ha létezik t darab n-ed rendû latin négyzetbôl álló ortogonális rendszer, akkor létezik olyan t+2 hosszúságú kódszavakból álló kód, amelynek minimális Hamming-távolsága t+1 és amelyben n 2 kódszó van. Két k hosszúságú kódszó a=(a 1, a 2...a k ) és b=(b 1, b 2...b k ) közötti Hamming távolság (jele = d(a,b)), azon i (i=1,2,...k) indexeknek a száma, amelyekre a i b i teljesül. Egy kódnak a minimális Hamming-távolsága a kódban szereplô összes kódszó párok közötti Hamming - távolságok minimuma. Alapvetô tételként kell e helyen megemlíteni, hogy egy q betûbôl álló ábécé feletti k hosszúságú d minimális Hamming-távolságú kódban maximum q k-d+1 kódszó lehet. Így a fent leírt Golomb-Posner kódban a kódszavak száma n t+2 (t+1)+1 =n 2, ami n-ed rendû latin négyzetek esetén maximális. 3. ábra Az ábrán látható kísérleti elrendezés azt jelenti, hogy például az A 1 állatnak elsô étkezésre T 1 takarmányt, másodikra T 2 takarmányt stb. kell adni. A kísérletsorozatban valóban fontos a teljes latin négyzet tulajdonság (ennek definíciója e cikk elsô részében található), hiszen ez biztosítja, hogy az összes lehetséges takarmány-sorrendet kipróbáljuk, ami éppen a kísérlet egyik lényeges célját képezi. 2. Kódolás-elméleti alkalmazások Érdekes megemlíteni, hogy az általánosan elterjedt nézetekkel szemben, nem Richard Wesley Hamming volt az elsô, aki 1950-ben a hibajelzô és javító kódokat bevezette (lásd a jobboldali képet), hanem Rudolf Schauffler akinek latin négyzetek alapján szerkesztett nem bináris hibajelzô és javító kódjai, valamint a latin négyzetek egyéb alkalmazásai már az 1946-ban benyújtott doktori diszszertációjában szerepeltek. Mivel Schauffler eredményei a titkosszolgálatnál töltött évei és a szigorú titoktartás következtében, szélesebb körben hozzáférhetô módon csak 1956-ban jelentek meg, így Hamming bináris hibajelzô és javító kódjait független eredménynek kell tekinteni. Schauffler gondolatait jóval késôbb viszontláthatjuk [1,5]. LIX. ÉVFOLYAM 2005/1 41
3 HÍRADÁSTECHNIKA A Golomb-Posner kód konstrukciója a következô példán jól követhetô: Legyen n=4, a konstrukcióhoz az L 1, L 2, L 3 páronként ortogonális negyedrendû latin négyzeteket használjuk fel (4. ábra). A konstrukció követhetôsége érdekében R 1 -nél a perem elemeket is feltüntettük. A konstrukció a latin négyzetekre alkalmazott Golomb-Posner eljárásnak értelemszerû analogonja. Az így kapott kód elemeit (kódszavait) a 7. ábrán láthatjuk. 4. ábra Látható módon L 1 -hez a keret elemeket is feltüntettük, mivel ennek a kódszavak képzése során jelentôsége lesz. A kódszavakat a következô módon képezzük: Az elsô komponens a sorkeret elem a i (i=1,2,3,4), a második komponens az oszlopkeret elem b j (j=1,2,3,4), majd sorrendben ezen keret elemek után következnek az L 1, L 2, L 3 latin négyzetek belsejében a i sor b j oszlop metszésénél lévô elemek. Így a 4. ábra L 1, L 2, L 3 latin négyzeteibôl az 5. ábrán lévô kódszó készlethez jutunk. Az olvasó ellenôrizheti, hogy a kódszavak száma 4 2 =16, a szóhossz 5, a minimális Hamming-távolság ábra Az elsô részben említett tized rendû latin négyzetekbôl álló ortogonális rendszer létrehozásának problémája (létezik-e három 10-ed rendû latin négyzetbôl álló ortogonális rendszer?) most a kódok nyelvére lefordítva így hangzik: van-e olyan Golomb-Posner kód, melyben a 10 elemû ábécé feletti kódszavak száma 100, hosszuk 5, és a kód minimális Hamming-távolsága 4? A Golomb-Posner kódok elônye, hogy n 2, illetve n 6 esetén tetszôleges n elemû ábécé felett léteznek. [2]-ben sikerült a Golomb-Posner féle konstrukciót ortogonális latin téglalapokra általánosítani A latin téglalap olyan téglalap mátrix, amely kiegészíthetô latin négyzetté. Két azonos méretû latin téglalapot akkor nevezünk ortogonálisnak, ha egymásra helyezve a megfelelô rendezett párok mind különbözôek. Példát mutatunk be a párok [2]-ban közölt konstrukciója alapján arra, hogy az R 1, R 2, R 3, R 4, R 5 2x6 méretû latin téglalapokból álló ortogonális rendszerbôl (6. ábra) milyen kód nyerhetô. 6. ábra 7. ábra A fenti konstrukció felhasználható személyi számok, jogosítvány, vagy ISBN számok, valamint más hasonló kódok elôállítására. Az ortogonális rendszer miatt a keletkezô kódszavak garantáltan különbözôek, az eljárás könnyen programozható, gyors elôállítást kínál. 3. Alkalmazások a távközlésben Egy mobiltelefon hálózati rendszerében egy nagyobb területet felosztanak kisebb területi egységekre és minden egységnek van egy telepített adó-vevô központja. Ez a központ a környezetében dolgozó adók üzenetét veszi és továbbítja egy másik központ felé. Természetesen a területi központ a más körzetbôl érkezô üzeneteket veszi és a saját területi egységén belül osztja szét, így sok frekvencia felhasználása szükséges egy ilyen rendszer üzemeltetéséhez. A felhasználható frekvenciák száma viszont korlátozott, valamint áthallási okok miatt az azonos frekvenciák egymáshoz közel fekvô adóknál nem alkalmazhatók. Ezért olyan célszerû frekvenciakiosztást kell javasolni, amely a frekvenciák ismételt felhasználásával csökkenti a szükséges frekvenciák számát és a lóugrásos latin négyzeteken alapuló frekvenciakiosztással megakadályozza mind az áthallást, mind a zavarást. A megoldást a cikk elsô részében említett Nasik-négyzet alkalmazása biztosítja. A 8. ábrán bemutatott Nasik-négyzet (ez egy olyan Nasik-négyzet amely egyben latin négyzet is és rendelkezik a lóugrás-tulajdonsággal) olyan tulajdonságú, hogy minden egyes eleme (egy elem egy frekvencia kiosztást reprezentál) nyolc olyan elemmel szomszédos, melyek közül két szomszédos elemhez nem rendelhetô azonos frekvencia. Az ábrán bemutatott latin négyzet ötödrendû, ez azt jelenti, hogy a javasolt eljárás használatához legalább öt különbözô frekvencia szükséges. Természetesen az egy adó-vevôhöz rendelt frekvenciák száma egynél jóval több is lehet. 8. ábra 42 LIX. ÉVFOLYAM 2005/1
4 Latin négyzetek alkalmazásai... Egy frekvencia-ugratásos hírközlô rendszer úgy jellemezhetô, hogy n frekvenciát használhat a rendszerben mûködô legfeljebb n adó. Az adók mindegyike bizonyos idôközönként frekvenciát vált a zavarás megnehezítése végett vagy egyéb okokból. A frekvenciaugratásos hírközlô rendszer akkor hatékony, ha a rendszerben mûködô adók egymástól függetlenül (külsô szinkronizálás nélkül) mûködhetnek azonos frekvenciákat használhatnak oly módon, hogy az ütközés (két adónak egy idôben azonos frekvencia használata) elkerülhetô legyen. R. D. Yates és G. R. Cooper már 1966-ban készített kutatási jelentésükben javasolták latin négyzetek alkalmazását a frekvencia-ugratás hatékonyságának növelésére. 4. Alkalmazás a digitális képkódolás és átvitel területén Egy (0,1) mátrixról akkor mondjuk, hogy uxv (u,v 2) horizontális ablak tulajdonsággal rendelkezik, ha egy u sorból és v oszlopból álló ablakot horizontálisan mozgatva a mátrixon, minden nem csupa nullából álló ablak legfeljebb egyszer fordul elô. (Hasonlóképpen definiáljuk a vertikális ablak tulajdonságot.) Egy mátrixot akkor mondunk uxv ablak tulajdonságúnak, ha horizontálisan és vertikálisan is uxv ablak tulajdonságú. Természetes általánosítása a fogalomnak, ha egy latin négyzettôl követeljük meg a horizontális, illetve vertikális ablak tulajdonságot. (0,1) mátrixokra az ablak tulajdonságot két Bell laboratóriumban dolgozó matematikus (F. J. MacWilliams, N. J. A. Sloane vizsgálták elôször. Az ablak tulajdonsággal rendelkezô mátrixok szerkesztésének gyakorlati alkalmazása is van, például a digitális képkódolás és átvitel területén. Most bemutatunk egy példát keresztül egy ablak tulajdonságokkal rendelkezô mátrix szerkesztést, amely mint látni fogjuk a teljes latin négyzeteken alapul. Tekintsünk egy negyedrendû teljes L 4 (a ij ) latin négyzetet (9. ábra), majd utolsó oszlopát megismételve, valamint egy kizárólag ötösöket tartalmazó oszlopot hozzávéve kapjuk a 10. ábrán látható M 4x6 (b ij ) mátrixot. 9. ábra 10. ábra Ateljes latin négyzet tulajdonságból következik, hogy úgy a 9. ábra L 4 (a ij ) latin négyzete, mint a 10. ábra M 4x6 (b ij ) kiterjesztése rendelkezik mind vertikális, mind horizontális 2x2 ablak tulajdonsággal. Vesszômentesnek nevezünk egy C kódot, amely n hosszúságú szavakból áll, ha bármely a 1...a n C és b 1...b n C esetén az a j a j+1...a n b 1 b 2...b j-1 (j=2,3,...,n) kódszavak egyike sincsen C-ben. Szemléltetô példaként a 10. ábra mátrixát és a 11. ábra bináris vesszômentes kódját felhasználva, az i, j c bij (i=1,2,3,4 j=1,2,3,4,5,6) megfeleltetéssel nyerjük a 12. ábrán látható (0,1) mátrixot, amely 14x1 ablak tulajdonságú. 11. ábra 12. ábra A fenti latin négyzeteket felhasználó szerkesztési mód részletes leírása megtalálható [3]-ban. 5. Latin négyzet alapú párhuzamos aritmetika A számítástechnika egyik égetô problémája a mûveletvégzési idôk lerövidítése. Ennek érdekében jöttek létre a különbözô párhuzamos mûveletet végzô architektúrák (pipeline processzorok, array processzorok stb.) Nem kaptak eddig megfelelô szerepet az úgynevezett maradék számrendszerbeli ábrázoláson alapuló aritmetikai egységek. Ilyen aritmetikai egység ismertetésére és a latin négyzetekkel való kapcsolatára derül fény a következôkben. Ezen példa kapcsán rámutatunk a latin négyzetek mûvelet táblaként való kódolási alkalmazására. A számok maradék számrendszerbeli ábrázolásának kezdetei az ókori Kínában keletkezett, úgynevezett kínai maradéktételen alapszik. Mivel e tétel több mint kétezer éves, nem természetes, hogy a soros mûveletvégzés lett a számítástechnika születésénél az elsô és napjainkig is alapvetôen elterjedt architektúra. Néhány olyan tudomány és technikatörténeti tényt igyekeztem [4] könyvemben közkincsé tenni, amelyek ezt a jelenséget még érdekesebbé teszik. Eme kevéssé ismert tények szerint már a XX. század elsô felében történt kísérlet a maradék számrendszerbeli ábrázoláson alapuló célgép (prímszám szita) készítésére, késôbb D. N. Lehmer, majd fia D. H. Lehmer hasonló célú és megoldású fotoelektronikus gépet épített. Az ifjabb Lehmer, aki ott volt az ENIAC születésénél, annak soros architektúrájúvá tételérôl a következôket írta: A következô dátumunk 1946, ami természetesen az ENIAC éve. Vajon felhasználható-e a nagysebességû számítógép a szita-módszer elvégzésére? Ez egy magas párhuzamosságú gép volt, amíg von Neumann el nem rontotta. A kínai maradék tétel: Pontosan egy olyan x<n természetes szám van melyre fennállnak a következô kongruenciák, x a 1 mod m 1, x a 2 mod m 2,., x a k mod m k, ha m 1,m 2,, m k páronként relatív prímek és n = m 1 m 2 m k. LIX. ÉVFOLYAM 2005/1 43
5 HÍRADÁSTECHNIKA Az x a i mod m i írásmód azt jelenti, hogy az x számot m i -vel osztva a i maradékot ad. Azt mondjuk, hogy az x szám maradék számrendszerbeli ábrázolása az (a 1 a 2.a k ) vektor. Az összeadás, kivonás, szorzás a maradék számrendszerben ábrázolt számok között komponensenként történik. Legyen x maradék számrendszerbeli ábrázolása (a 1 a 2.a k ) és y ábrázolása (b 1 b 2.b k ), akkor x+y ábrázolása (a 1 b 1 a 2 b 2 a k b k ), ahol a mûvelet a mod n i (i = 1,2,...,k) összeadást jelenti. Hasonló módon értelmezhetô a kivonás és a szorzás is. A 13. ábra bemutatja a 0-15 közé esô egész számok 3 és 5 modulusra vonatkozó maradék számrendszerbeli alakjait, majd egy példán keresztül érzékeltetem a maradék számrendszerben való összeadást. Eme táblázat segítségével már képes bárki ebbe a szám intervallumba esô számokkal mûveleteket végezni, ezáltal megtapasztalni azt a meghökkentô lehetôséget, amit a párhuzamos számítás (párhuzamos aritmetika) jelent. 13. ábra Táblázat a 0-29 természetes számok maradék számrendszerbeli ábrázolására A maradék számrendszerben az összeadás, vagy a kivonás sokkal gyorsabban, valóban az összes számjegyen szinte egyszerre (párhuzamosan) elvégezhetô, mivel nincs átvitel. Illusztrációként a 14. ábrán bemutatjuk a következô mûveletek elvégzését modulus rendszerben: 7+3+1= ábra Az összeadás eredménye (2,1) a 13. ábra 11. sorában megtalálható, vagyis a modulus alakban kapott eredmény valóban a tízes számrendszerben kiszámított 11-nek felel meg. A kínai maradék tétel tehát ad egy olyan szám ábrázolási módot, amelynek segítségével a párhuzamos mûveletvégzés könnyen megvalósítható. A modulus aritmetika mûveleteihez tartozó mûvelet táblák egy-egy latin négyzetet alkotnak. A fent bemutatott mod 3, illetve mod 5 összeadáshoz tartozó mûvelet táblákat mutatják a 15. ábrán látható peremezett latin négyzetek: 15. ábra Most példát adunk a mod 3 és mod 5 modulus aritmetikabeli szorzásra, illetve a szorzás elvégzéséhez szükséges mûvelettáblákra, amelyek a perem sor, illetve oszlop elhagyásával latin négyzetet alkotnak (16. ábra). 16. ábra Az összeadásnál bemutatott 13. ábra szerint: 3=(0,3), 5=(2,0), ekkor 3 5=(0 3 2, 3 5 0)=(0,0), amely a táblázat 15. sorában található, tehát a szorzás eredménye 15, ami megfelel a tízes számrendszerbelinek. A bemutatott példákból is kiderül, hogy a modulus aritmetika használatának fô nehézségét a túlcsordulás, valamint az elôjel jelzése és a maradék számrendszerbeli ábrázolásból a tízes számrendszerbe és viszont konvertálás viszonylagos lassúsága jelenti. Ezt az ábrázolás módot tehát ott célszerû alkalmazni, ahol a számolás igény nagy és csak ritkán kell konvertálni a számokat. Irodalom [1] A. M. Andrew: Decimal error-correction: a solution, Computer J. 18 (1975), pp [2] J. Dénes: Latin squares and non-binary encoding, Proc. Conf. Inform. Theory (Cachen, France, 1977), CNRS, Paris 1979., pp [3] J. Dénes, A. D. Keedwell: A new construction of twodimensional araye with window property, IEEE Trans., On Information Theory [4] Dénes Tamás: Titkos-számítógép-történet, Aranykönyv Kiadó, Budapest, [5] A. Ecker, G. Poch: Check character systems, Computing 37(1986), pp [6] D. R. Hughes, F. C. Piper: Design theory, Cambridge University Press, [7] D. H. Lehmer: A photo-electric number sieve, Amer. Math. Monthly 40 (1933), pp [8] D.H.Lehmer: A machine for combining sets of linear conqruences, Mathematische Annalen 109 (1934), pp [9] R. Mandl: Orthogonal latin squares: an application of experimental design to compiler testing, Comm. ACM 28(1985), pp LIX. ÉVFOLYAM 2005/1
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
1. előadás. Lineáris algebra numerikus módszerei. Hibaszámítás Számábrázolás Kerekítés, levágás Klasszikus hibaanalízis Abszolút hiba Relatív hiba
 Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez
 Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, sandor.tamas@kvk.bmf.hu Takács Gergely, takacs.gergo@kvk.bmf.hu Lektorálta: dr. Schuster György PhD, hal@k2.jozsef.kando.hu
Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, sandor.tamas@kvk.bmf.hu Takács Gergely, takacs.gergo@kvk.bmf.hu Lektorálta: dr. Schuster György PhD, hal@k2.jozsef.kando.hu
2. Fejezet : Számrendszerek
 2. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College
2. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College
The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003
 . Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach. kiadás, Irv Englander John Wiley and Sons Wilson Wong, Bentley College Linda Senne,
. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach. kiadás, Irv Englander John Wiley and Sons Wilson Wong, Bentley College Linda Senne,
4. Fejezet : Az egész számok (integer) ábrázolása
 4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 207. tavasz. Diszkrét matematika 2.C szakirány 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 207.
Diszkrét matematika 2.C szakirány 207. tavasz. Diszkrét matematika 2.C szakirány 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 207.
A valós számok halmaza
 VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
Számelmélet. 4. Igazolja, hogy ha hat egész szám összege páratlan, akkor e számok szorzata páros!
 Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
I. VEKTOROK, MÁTRIXOK
 217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
Diszkrét matematika II., 8. előadás. Vektorterek
 1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
Gráfelmélet. I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma
 Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
3. gyakorlat. Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F}
 3. gyakorlat Számrendszerek: Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F} Alaki érték: 0, 1, 2,..., 9,... Helyi
3. gyakorlat Számrendszerek: Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F} Alaki érték: 0, 1, 2,..., 9,... Helyi
KÓDOLÁSTECHNIKA PZH. 2006. december 18.
 KÓDOLÁSTECHNIKA PZH 2006. december 18. 1. Hibajavító kódolást tekintünk. Egy lineáris bináris blokk kód generátormátrixa G 10110 01101 a.) Adja meg a kód kódszavait és paramétereit (n, k,d). (3 p) b.)
KÓDOLÁSTECHNIKA PZH 2006. december 18. 1. Hibajavító kódolást tekintünk. Egy lineáris bináris blokk kód generátormátrixa G 10110 01101 a.) Adja meg a kód kódszavait és paramétereit (n, k,d). (3 p) b.)
Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit.
 2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
Számelméleti alapfogalmak
 1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Diszkrét matematika I., 12. előadás Dr. Takách Géza NyME FMK Informatikai Intézet takach november 30.
 1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2016. ősz 1. Diszkrét matematika 2.C szakirány 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2016.
Diszkrét matematika 2.C szakirány 2016. ősz 1. Diszkrét matematika 2.C szakirány 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2016.
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Negatív alapú számrendszerek
 2015. március 4. Negatív számok Legyen b > 1 egy adott egész szám. Ekkor bármely N 0 egész szám egyértelműen felírható N = m a k b k k=1 alakban, ahol 0 a k < b egész szám. Negatív számok Legyen b > 1
2015. március 4. Negatív számok Legyen b > 1 egy adott egész szám. Ekkor bármely N 0 egész szám egyértelműen felírható N = m a k b k k=1 alakban, ahol 0 a k < b egész szám. Negatív számok Legyen b > 1
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2.
 Diszkrét matematika 2. 2019. május 3. 1. Diszkrét matematika 2. 10. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Mérai László diái alapján Komputeralgebra Tanszék 2019. május
Diszkrét matematika 2. 2019. május 3. 1. Diszkrét matematika 2. 10. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Mérai László diái alapján Komputeralgebra Tanszék 2019. május
Mátrixok február Feladat: Legyen A = ( ( B =
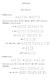 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Az Informatika Elméleti Alapjai
 Az Informatika Elméleti Alapjai dr. Kutor László Minimális redundanciájú kódok Statisztika alapú tömörítő algoritmusok http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 BMF
Az Informatika Elméleti Alapjai dr. Kutor László Minimális redundanciájú kódok Statisztika alapú tömörítő algoritmusok http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 BMF
Műveletek mátrixokkal. Kalkulus. 2018/2019 ősz
 2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
Számítógép felépítése
 Alaplap, processzor Számítógép felépítése Az alaplap A számítógép teljesítményét alapvetően a CPU és belső busz sebessége (a belső kommunikáció sebessége), a memória mérete és típusa, a merevlemez sebessége
Alaplap, processzor Számítógép felépítése Az alaplap A számítógép teljesítményét alapvetően a CPU és belső busz sebessége (a belső kommunikáció sebessége), a memória mérete és típusa, a merevlemez sebessége
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Elemi számelmélet Diszkrét matematika I. középszint
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Elemi számelmélet Diszkrét matematika I. középszint
Hibajavító kódolás (előadásvázlat, 2012. november 14.) Maróti Miklós
 Hibajavító kódolás (előadásvázlat, 2012 november 14) Maróti Miklós Ennek az előadásnak a megértéséhez a következő fogalmakat kell tudni: test, monoid, vektortér, dimenzió, mátrixok Az előadáshoz ajánlott
Hibajavító kódolás (előadásvázlat, 2012 november 14) Maróti Miklós Ennek az előadásnak a megértéséhez a következő fogalmakat kell tudni: test, monoid, vektortér, dimenzió, mátrixok Az előadáshoz ajánlott
13. Egy x és egy y hosszúságú sorozat konvolúciójának hossza a. x-y-1 b. x-y c. x+y d. x+y+1 e. egyik sem
 1. A Huffman-kód prefix és forráskiterjesztéssel optimálissá tehető, ezért nem szükséges hozzá a forrás valószínűség-eloszlásának ismerete. 2. Lehet-e tökéletes kriptorendszert készíteni? Miért? a. Lehet,
1. A Huffman-kód prefix és forráskiterjesztéssel optimálissá tehető, ezért nem szükséges hozzá a forrás valószínűség-eloszlásának ismerete. 2. Lehet-e tökéletes kriptorendszert készíteni? Miért? a. Lehet,
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
Flynn féle osztályozás Single Isntruction Multiple Instruction Single Data SISD SIMD Multiple Data MISD MIMD
 M5-. A lineáris algebra párhuzamos algoritmusai. Ismertesse a párhuzamos gépi architektúrák Flynn-féle osztályozását. A párhuzamos lineáris algebrai algoritmusok között mi a BLAS csomag célja, melyek annak
M5-. A lineáris algebra párhuzamos algoritmusai. Ismertesse a párhuzamos gépi architektúrák Flynn-féle osztályozását. A párhuzamos lineáris algebrai algoritmusok között mi a BLAS csomag célja, melyek annak
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Következik, hogy B-nek minden prímosztója 4k + 1 alakú, de akkor B maga is 4k + 1 alakú, s ez ellentmondás.
 Prímszámok A (pozitív) prímszámok sorozata a következő: 2, 3, 5, 7, 11, 13, 17, 19,... 1. Tétel. Végtelen sok prímszám van. Első bizonyítás. (Euklidész) Tegyük fel, hogy állításunk nem igaz, tehát véges
Prímszámok A (pozitív) prímszámok sorozata a következő: 2, 3, 5, 7, 11, 13, 17, 19,... 1. Tétel. Végtelen sok prímszám van. Első bizonyítás. (Euklidész) Tegyük fel, hogy állításunk nem igaz, tehát véges
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
A továbbiakban Y = {0, 1}, azaz minden szóhoz egy bináris sorozatot rendelünk
 1. Kódelmélet Legyen X = {x 1,..., x n } egy véges, nemüres halmaz. X-et ábécének, elemeit betűknek hívjuk. Az X elemeiből képzett v = y 1... y m sorozatokat X feletti szavaknak nevezzük; egy szó hosszán
1. Kódelmélet Legyen X = {x 1,..., x n } egy véges, nemüres halmaz. X-et ábécének, elemeit betűknek hívjuk. Az X elemeiből képzett v = y 1... y m sorozatokat X feletti szavaknak nevezzük; egy szó hosszán
1.) Csaba egy 86 oldalas könyv 50 oldalát elolvasta. Hány nap alatt fejezi be a könyvet ha egy nap 9 oldalt olvas belőle? A) 6 B) 4 C) 3 D) 5
 WWW.ORCHIDEA.HU 1 1.) Csaba egy 86 oldalas könyv 50 oldalát elolvasta. Hány nap alatt fejezi be a könyvet ha egy nap 9 oldalt olvas belőle? A) 6 B) 4 C) 3 D) 5 2.) Számítsd ki a végeredményt: 1 1 1 1 1
WWW.ORCHIDEA.HU 1 1.) Csaba egy 86 oldalas könyv 50 oldalát elolvasta. Hány nap alatt fejezi be a könyvet ha egy nap 9 oldalt olvas belőle? A) 6 B) 4 C) 3 D) 5 2.) Számítsd ki a végeredményt: 1 1 1 1 1
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Minden egész szám osztója önmagának, azaz a a minden egész a-ra.
 1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Hibajavító kódok május 31. Hibajavító kódok 1. 1
 Hibajavító kódok 2007. május 31. Hibajavító kódok 1. 1 Témavázlat Hibajavító kódolás Blokk-kódok o Hamming-távolság, Hamming-súly o csoportkód o S n -beli u középpontú t sugarú gömb o hibajelzı képesség
Hibajavító kódok 2007. május 31. Hibajavító kódok 1. 1 Témavázlat Hibajavító kódolás Blokk-kódok o Hamming-távolság, Hamming-súly o csoportkód o S n -beli u középpontú t sugarú gömb o hibajelzı képesség
Informatikai Rendszerek Alapjai
 Informatikai Rendszerek Alapjai Dr. Kutor László A redundancia fogalma és mérése Minimális redundanciájú kódok 1. http://uni-obuda.hu/users/kutor/ IRA 2014 könyvtár Óbudai Egyetem, NIK Dr. Kutor László
Informatikai Rendszerek Alapjai Dr. Kutor László A redundancia fogalma és mérése Minimális redundanciájú kódok 1. http://uni-obuda.hu/users/kutor/ IRA 2014 könyvtár Óbudai Egyetem, NIK Dr. Kutor László
XXII. Vályi Gyula Emlékverseny április 8. V. osztály
 V. osztály 1. Egy anya éveinek száma ugyanannyi, mint a lánya életkora hónapokban kifejezve. Mennyi idősek külön-külön, ha az anya 23 évvel és 10 hónappal idősebb a lányánál? 2. Melyek azok a 2016-nál
V. osztály 1. Egy anya éveinek száma ugyanannyi, mint a lánya életkora hónapokban kifejezve. Mennyi idősek külön-külön, ha az anya 23 évvel és 10 hónappal idősebb a lányánál? 2. Melyek azok a 2016-nál
Pótvizsga anyaga 5. osztály (Iskola honlapján is megtalálható!) Pótvizsga: beadandó feladatok 45 perces írásbeli szóbeli a megadott témakörökből
 Pótvizsga anyaga 5. osztály (Iskola honlapján is megtalálható!) Természetes számok: 0123 (TK 4-49.oldal) - tízes számrendszer helyi értékei alaki érték valódi érték - becslés kerekítés - alapműveletek:
Pótvizsga anyaga 5. osztály (Iskola honlapján is megtalálható!) Természetes számok: 0123 (TK 4-49.oldal) - tízes számrendszer helyi értékei alaki érték valódi érték - becslés kerekítés - alapműveletek:
Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem.
 Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem. Elemi esemény: a kísérlet egyes lehetséges egyes lehetséges kimenetelei.
Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem. Elemi esemény: a kísérlet egyes lehetséges egyes lehetséges kimenetelei.
SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA
 SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA BINÁRIS (kettes) ÉS HEXADECIMÁLIS (tizenhatos) SZÁMRENDSZEREK (HELYIÉRTÉK, ÁTVÁLTÁSOK, MŰVELETEK) A KETTES SZÁMRENDSZER A computerek világában a
SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA BINÁRIS (kettes) ÉS HEXADECIMÁLIS (tizenhatos) SZÁMRENDSZEREK (HELYIÉRTÉK, ÁTVÁLTÁSOK, MŰVELETEK) A KETTES SZÁMRENDSZER A computerek világában a
A fejlesztés várt eredményei a 1. évfolyam végén
 A tanuló legyen képes: A fejlesztés várt eredményei a 1. évfolyam végén - Halmazalkotásra, összehasonlításra az elemek száma szerint; - Állítások igazságtartalmának eldöntésére, állítások megfogalmazására;
A tanuló legyen képes: A fejlesztés várt eredményei a 1. évfolyam végén - Halmazalkotásra, összehasonlításra az elemek száma szerint; - Állítások igazságtartalmának eldöntésére, állítások megfogalmazására;
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
STATISZTIKA. A maradék független a kezelés és blokk hatástól. Maradékok leíró statisztikája. 4. A modell érvényességének ellenőrzése
 4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
Harmadik gyakorlat. Számrendszerek
 Harmadik gyakorlat Számrendszerek Ismétlés Tízes (decimális) számrendszer: 2 372 =3 2 +7 +2 alakiérték valódi érték = aé hé helyiérték helyiértékek a tízes szám hatványai, a számjegyek így,,2,,8,9 Kettes
Harmadik gyakorlat Számrendszerek Ismétlés Tízes (decimális) számrendszer: 2 372 =3 2 +7 +2 alakiérték valódi érték = aé hé helyiérték helyiértékek a tízes szám hatványai, a számjegyek így,,2,,8,9 Kettes
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
DIGITÁLIS TECHNIKA I BINÁRIS SZÁMRENDSZER BEVEZETŐ ÁTTEKINTÉS BINÁRIS SZÁMRENDSZER HELYÉRTÉK. Dr. Lovassy Rita Dr.
 26..5. DIGITÁLIS TEHNIK I Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet INÁRIS SZÁMRENDSZER 5. ELŐDÁS 2 EVEZETŐ ÁTTEKINTÉS 6. előadás témája a digitális rendszerekben
26..5. DIGITÁLIS TEHNIK I Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet INÁRIS SZÁMRENDSZER 5. ELŐDÁS 2 EVEZETŐ ÁTTEKINTÉS 6. előadás témája a digitális rendszerekben
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
A számítástechnika fejlődése
 A számítástechnika fejlődése Az 1600-as évektől kezdődően az emberek igyekeztek olyan gépeket építeni, melyek megkönnyítik a számolást. A számítógépek fejlődését nagy lépésekben követjük. Az egymástól
A számítástechnika fejlődése Az 1600-as évektől kezdődően az emberek igyekeztek olyan gépeket építeni, melyek megkönnyítik a számolást. A számítógépek fejlődését nagy lépésekben követjük. Az egymástól
Dr. Oniga István DIGITÁLIS TECHNIKA 2
 Dr. Oniga István DIGITÁLIS TECHNIKA 2 Számrendszerek A leggyakrabban használt számrendszerek: alapszám számjegyek Tízes (decimális) B = 10 0, 1, 8, 9 Kettes (bináris) B = 2 0, 1 Nyolcas (oktális) B = 8
Dr. Oniga István DIGITÁLIS TECHNIKA 2 Számrendszerek A leggyakrabban használt számrendszerek: alapszám számjegyek Tízes (decimális) B = 10 0, 1, 8, 9 Kettes (bináris) B = 2 0, 1 Nyolcas (oktális) B = 8
+ 3 5 2 3 : 1 4 : 1 1 A ) B ) C ) D ) 93
 . Mennyi az alábbi művelet eredménye? 4 + 4 : 5 : 5 + 8 07 9 A ) B ) C ) D ) E ) 9 9 9 9 9. Egy digitális órát (amely 4 órás üzemmódban működik) pontosan beállítottunk. Kiderült azonban, hogy egy nap átlagosan
. Mennyi az alábbi művelet eredménye? 4 + 4 : 5 : 5 + 8 07 9 A ) B ) C ) D ) E ) 9 9 9 9 9. Egy digitális órát (amely 4 órás üzemmódban működik) pontosan beállítottunk. Kiderült azonban, hogy egy nap átlagosan
Alapfogalmak a Diszkrét matematika II. tárgyból
 Alapfogalmak a Diszkrét matematika II. tárgyból (A szakirány, 2015-2016 tavaszi félév) A számonkérés során ezeknek a definícióknak, tételkimondásoknak az alapos megértését is számon kérjük. A példakérdések
Alapfogalmak a Diszkrét matematika II. tárgyból (A szakirány, 2015-2016 tavaszi félév) A számonkérés során ezeknek a definícióknak, tételkimondásoknak az alapos megértését is számon kérjük. A példakérdések
Bevezetés az informatikába gyakorló feladatok Utoljára módosítva:
 Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 12 3.1. Megoldások... 14 A gyakorlósor lektorálatlan,
Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 12 3.1. Megoldások... 14 A gyakorlósor lektorálatlan,
2015. évi Bolyai János Megyei Matematikaverseny MEGOLDÁSI ÉS ÉRTÉKELÉSI ÚTMUTATÓ 9. osztály
 A közölt megoldási utak a feladatoknak nem az egyetlen helyes megoldási módját adják meg, több eltérő megoldás is lehetséges. Az útmutatótól eltérő megoldásokat a kialakult tanári gyakorlat alapján, az
A közölt megoldási utak a feladatoknak nem az egyetlen helyes megoldási módját adják meg, több eltérő megoldás is lehetséges. Az útmutatótól eltérő megoldásokat a kialakult tanári gyakorlat alapján, az
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
Matematika. 1. osztály. 2. osztály
 Matematika 1. osztály - képes halmazokat összehasonlítani az elemek száma szerint, halmazt alkotni; - képes állítások igazságtartalmának eldöntésére, állításokat megfogalmazni; - halmazok elemeit összehasonlítja,
Matematika 1. osztály - képes halmazokat összehasonlítani az elemek száma szerint, halmazt alkotni; - képes állítások igazságtartalmának eldöntésére, állításokat megfogalmazni; - halmazok elemeit összehasonlítja,
Klasszikus algebra előadás. Waldhauser Tamás április 28.
 Klasszikus algebra előadás Waldhauser Tamás 2014. április 28. 5. Számelmélet integritástartományokban Oszthatóság Mostantól R mindig tetszőleges integritástartományt jelöl. 5.1. Definíció. Azt mondjuk,
Klasszikus algebra előadás Waldhauser Tamás 2014. április 28. 5. Számelmélet integritástartományokban Oszthatóság Mostantól R mindig tetszőleges integritástartományt jelöl. 5.1. Definíció. Azt mondjuk,
Irodalom. (a) A T, B T, (b) A + B, C + D, D C, (c) 3A, (d) AD, DA, B T A, 1 2 B = 1 C = A = 1 0 D = (a) 1 1 3, B T = = ( ) ; A T = 1 0
 Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév
 Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév Az informatika története (ebből a fejezetből csak a félkövér betűstílussal szedett részek kellenek) 1. Számítástechnika
Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév Az informatika története (ebből a fejezetből csak a félkövér betűstílussal szedett részek kellenek) 1. Számítástechnika
Elemi matematika szakkör
 Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Mohó algoritmusok. Példa:
 Mohó algoritmusok Optimalizálási probléma megoldására szolgáló algoritmus sokszor olyan lépések sorozatából áll, ahol minden lépésben adott halmazból választhatunk. Ezt gyakran dinamikus programozás alapján
Mohó algoritmusok Optimalizálási probléma megoldására szolgáló algoritmus sokszor olyan lépések sorozatából áll, ahol minden lépésben adott halmazból választhatunk. Ezt gyakran dinamikus programozás alapján
A szabályos sokszögek közelítő szerkesztéséhez
 1 A szabályos sokszögek közelítő szerkesztéséhez A síkmértani szerkesztések között van egy kedvencünk: a szabályos n - szög közelítő szerkesztése. Azért vívta ki nálunk ezt az előkelő helyet, mert nagyon
1 A szabályos sokszögek közelítő szerkesztéséhez A síkmértani szerkesztések között van egy kedvencünk: a szabályos n - szög közelítő szerkesztése. Azért vívta ki nálunk ezt az előkelő helyet, mert nagyon
Mechatronika Modul 1: Alapismeretek
 Mechatronika Modul : Alapismeretek Oktatói segédlet (Elképzelés) Készítették: Matthias Römer Chemnitz-i Műszaki Egyetem, Szerszámgépek és Gyártási Folyamatok Intézete, Németország Cser Adrienn Corvinus
Mechatronika Modul : Alapismeretek Oktatói segédlet (Elképzelés) Készítették: Matthias Römer Chemnitz-i Műszaki Egyetem, Szerszámgépek és Gyártási Folyamatok Intézete, Németország Cser Adrienn Corvinus
Determinánsok. A determináns fogalma olyan algebrai segédeszköz, amellyel. szolgáltat az előbbi kérdésekre, bár ez nem mindig hatékony.
 Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Szakács Lili Kata megoldása
 1. feladat Igazoljuk, hogy minden pozitív egész számnak van olyan többszöröse, ami 0-tól 9-ig az összes számjegyet tartalmazza legalább egyszer! Andó Angelika megoldása Áll.: minden a Z + -nak van olyan
1. feladat Igazoljuk, hogy minden pozitív egész számnak van olyan többszöröse, ami 0-tól 9-ig az összes számjegyet tartalmazza legalább egyszer! Andó Angelika megoldása Áll.: minden a Z + -nak van olyan
PRÓBAÉRETTSÉGI 2004.május MATEMATIKA. KÖZÉPSZINT II. 135 perc
 PRÓBAÉRETTSÉGI 2004.május MATEMATIKA KÖZÉPSZINT II. 135 perc A feladatok megoldására 135 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A II/B
PRÓBAÉRETTSÉGI 2004.május MATEMATIKA KÖZÉPSZINT II. 135 perc A feladatok megoldására 135 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A II/B
összeadjuk 0-t kapunk. Képletben:
 814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
1.1. Alapfeladatok. hogy F 1 = 1, F 2 = 1 és általában F n+2 = F n+1 + F n (mert a jobboldali ág egy szinttel lennebb van, mint a baloldali).
 1.1. Alapfeladatok 1.1.1. Megoldás. Jelöljük F n -el az n-ed rendű nagyapák számát. Az ábra alapján látható, hogy F 1 = 1, F = 1 és általában F n+ = F n+1 + F n mert a jobboldali ág egy szinttel lennebb
1.1. Alapfeladatok 1.1.1. Megoldás. Jelöljük F n -el az n-ed rendű nagyapák számát. Az ábra alapján látható, hogy F 1 = 1, F = 1 és általában F n+ = F n+1 + F n mert a jobboldali ág egy szinttel lennebb
26. MINIMÁLIS KÖLTSÉGŰ UTAK MINDEN CSÚCSPÁRRA
 26. MINIMÁLIS KÖLTSÉGŰ UTAK MINDEN CSÚCSPÁRRA Az előző két fejezetben tárgyalt feladat általánosításaként a gráfban található összes csúcspárra szeretnénk meghatározni a legkisebb költségű utat. A probléma
26. MINIMÁLIS KÖLTSÉGŰ UTAK MINDEN CSÚCSPÁRRA Az előző két fejezetben tárgyalt feladat általánosításaként a gráfban található összes csúcspárra szeretnénk meghatározni a legkisebb költségű utat. A probléma
SZÁMÍTÓGÉPEK BELSŐ FELÉPÍTÉSE - 1
 INFORMATIKAI RENDSZEREK ALAPJAI (INFORMATIKA I.) 1 NEUMANN ARCHITEKTÚRÁJÚ GÉPEK MŰKÖDÉSE SZÁMÍTÓGÉPEK BELSŐ FELÉPÍTÉSE - 1 Ebben a feladatban a következőket fogjuk áttekinteni: Neumann rendszerű számítógép
INFORMATIKAI RENDSZEREK ALAPJAI (INFORMATIKA I.) 1 NEUMANN ARCHITEKTÚRÁJÚ GÉPEK MŰKÖDÉSE SZÁMÍTÓGÉPEK BELSŐ FELÉPÍTÉSE - 1 Ebben a feladatban a következőket fogjuk áttekinteni: Neumann rendszerű számítógép
A Peano-görbe. Besenyei Ádám ELTE
 A Peano-görbe Besenyei Ádám ELTE A folytonos görbe kifejezés hallatán hajlamosak vagyunk először egy, a szó szoros értelmében egybefüggően megrajzolható vonalra gondolni. A görbe fogalma azonban a vártnál
A Peano-görbe Besenyei Ádám ELTE A folytonos görbe kifejezés hallatán hajlamosak vagyunk először egy, a szó szoros értelmében egybefüggően megrajzolható vonalra gondolni. A görbe fogalma azonban a vártnál
Felvételi tematika INFORMATIKA
 Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
2013.11.25. H=0 H=1. Legyen m pozitív egészre {a 1, a 2,, a m } különböző üzenetek halmaza. Ha az a i üzenetet k i -szer fordul elő az adásban,
 Legyen m pozitív egészre {a 1, a 2,, a m } különböző üzenetek halmaza. Ha az a i üzenetet k i -szer fordul elő az adásban, akkor a i (gyakorisága) = k i a i relatív gyakorisága: A jel információtartalma:
Legyen m pozitív egészre {a 1, a 2,, a m } különböző üzenetek halmaza. Ha az a i üzenetet k i -szer fordul elő az adásban, akkor a i (gyakorisága) = k i a i relatív gyakorisága: A jel információtartalma:
1/50. Teljes indukció 1. Back Close
 1/50 Teljes indukció 1 A teljes indukció talán a legfontosabb bizonyítási módszer a számítástudományban. Teljes indukció elve. Legyen P (n) egy állítás. Tegyük fel, hogy (1) P (0) igaz, (2) minden n N
1/50 Teljes indukció 1 A teljes indukció talán a legfontosabb bizonyítási módszer a számítástudományban. Teljes indukció elve. Legyen P (n) egy állítás. Tegyük fel, hogy (1) P (0) igaz, (2) minden n N
Assembly programozás: 2. gyakorlat
 Assembly programozás: 2. gyakorlat Számrendszerek: Kettes (bináris) számrendszer: {0, 1} Nyolcas (oktális) számrendszer: {0,..., 7} Tízes (decimális) számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális
Assembly programozás: 2. gyakorlat Számrendszerek: Kettes (bináris) számrendszer: {0, 1} Nyolcas (oktális) számrendszer: {0,..., 7} Tízes (decimális) számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális
Diszkrét matematika 2.
 Diszkrét matematika 2. Mérai László előadása alapján Készítette: Nagy Krisztián 4. előadás Eulerséta: Olyan séta, mely a gráf minden élét pontosan egyszer tartalmazza. Tétel: egy összefüggő gráf. Ha minden
Diszkrét matematika 2. Mérai László előadása alapján Készítette: Nagy Krisztián 4. előadás Eulerséta: Olyan séta, mely a gráf minden élét pontosan egyszer tartalmazza. Tétel: egy összefüggő gráf. Ha minden
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. ősz 1. Diszkrét matematika 2.C szakirány 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Diszkrét matematika 2.C szakirány 2017. ősz 1. Diszkrét matematika 2.C szakirány 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
7. gyakorlat. Lineáris algebrai egyenletrendszerek megoldhatósága
 7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
Bevezetés az informatikába gyakorló feladatok Utoljára módosítva:
 Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 10 3.1. Megoldások... 12 A gyakorlósor lektorálatlan,
Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 10 3.1. Megoldások... 12 A gyakorlósor lektorálatlan,
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 3 III. MEGFELELTETÉSEk, RELÁCIÓk 1. BEVEZETÉS Emlékeztetünk arra, hogy az rendezett párok halmazát az és halmazok Descartes-féle szorzatának nevezzük. Más szóval az és halmazok
KOVÁCS BÉLA, MATEmATIkA I. 3 III. MEGFELELTETÉSEk, RELÁCIÓk 1. BEVEZETÉS Emlékeztetünk arra, hogy az rendezett párok halmazát az és halmazok Descartes-féle szorzatának nevezzük. Más szóval az és halmazok
Törtek. Rendelhetőek nagyon jó szemléltethető eszközök könyvesboltokban és internetek is, pl:
 Törtek A törteknek kétféle értelmezése van: - Egy egészet valamennyi részre (nevező) osztunk, és abból kiválasztunk valahány darabot (számláló) - Valamennyi egészet (számláló), valahány részre osztunk
Törtek A törteknek kétféle értelmezése van: - Egy egészet valamennyi részre (nevező) osztunk, és abból kiválasztunk valahány darabot (számláló) - Valamennyi egészet (számláló), valahány részre osztunk
5. Fejezet : Lebegőpontos számok. Lebegőpontos számok
 5. Fejezet : Lebegőpontos The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College Linda
5. Fejezet : Lebegőpontos The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College Linda
Typotex Kiadó. Bevezetés
 Bevezetés A bennünket körülvevő világ leírásához ősidők óta számokat is alkalmazunk. Tekintsük át a számfogalom kiépülésének logikai-történeti folyamatát, amely minden valószínűség szerint a legkorábban
Bevezetés A bennünket körülvevő világ leírásához ősidők óta számokat is alkalmazunk. Tekintsük át a számfogalom kiépülésének logikai-történeti folyamatát, amely minden valószínűség szerint a legkorábban
Új műveletek egy háromértékű logikában
 A Magyar Tudomány Napja 2012. Új műveletek egy háromértékű logikában Dr. Szász Gábor és Dr. Gubán Miklós Tartalom A probléma előzményei A hagyományos műveletek Az új műveletek koncepciója Alkalmazási példák
A Magyar Tudomány Napja 2012. Új műveletek egy háromértékű logikában Dr. Szász Gábor és Dr. Gubán Miklós Tartalom A probléma előzményei A hagyományos műveletek Az új műveletek koncepciója Alkalmazási példák
Hadamard-mátrixok Előadó: Hajnal Péter február 23.
 Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Általános algoritmustervezési módszerek
 Általános algoritmustervezési módszerek Ebben a részben arra mutatunk példát, hogy miként használhatóak olyan általános algoritmustervezési módszerek mint a dinamikus programozás és a korlátozás és szétválasztás
Általános algoritmustervezési módszerek Ebben a részben arra mutatunk példát, hogy miként használhatóak olyan általános algoritmustervezési módszerek mint a dinamikus programozás és a korlátozás és szétválasztás
Felvételi vizsga mintatételsor Informatika írásbeli vizsga
 BABEȘ BOLYAI TUDOMÁNYEGYETEM MATEMATIKA ÉS INFORMATIKA KAR A. tételsor (30 pont) Felvételi vizsga mintatételsor Informatika írásbeli vizsga 1. (5p) Egy x biten tárolt egész adattípus (x szigorúan pozitív
BABEȘ BOLYAI TUDOMÁNYEGYETEM MATEMATIKA ÉS INFORMATIKA KAR A. tételsor (30 pont) Felvételi vizsga mintatételsor Informatika írásbeli vizsga 1. (5p) Egy x biten tárolt egész adattípus (x szigorúan pozitív
;3 ; 0; 1 7; ;7 5; 3. pozitív: ; pozitív is, negatív is: ;
 . A racion lis sz mok A tanult sz mok halmaza A) Ábrázold számegyenesen az alábbi számokat! 8 + + 0 + 7 0 7 7 0 0. 0 Válogasd szét a számokat aszerint, hogy pozitív: pozitív is, negatív is: negatív: sem
. A racion lis sz mok A tanult sz mok halmaza A) Ábrázold számegyenesen az alábbi számokat! 8 + + 0 + 7 0 7 7 0 0. 0 Válogasd szét a számokat aszerint, hogy pozitív: pozitív is, negatív is: negatív: sem
Arany Dániel Matematikai Tanulóverseny 2012/2013-as tanév 1. forduló haladók III. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 0/03-as tanév. forduló haladók III. kategória Megoldások és javítási útmutató. Egy kör kerületére felírjuk -től 3-ig az egészeket
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 0/03-as tanév. forduló haladók III. kategória Megoldások és javítási útmutató. Egy kör kerületére felírjuk -től 3-ig az egészeket
A SZÁMFOGALOM KIALAKÍTÁSA
 A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
